انتگرال و قواعد آن در ریاضیات چیست؟ موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد و اهمیت آن بر داوطلبان پوشیده نیست. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید. انتگرال از مباحث مهم ریاضی است. در این مطلب با انتگرال و قواعد آن در ریاضیات آشنا میشوید.
در وبلاگ کافهتدریس برخی از موضوعهای مهم دروس را با نگاه آموزشی و به صورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید.
در این مطلب به سراغ انتگرال و قواعد آن در ریاضیات رفتهایم.
انتگرال
در ریاضیات انتگرال (به فرانسوی: Integral)، روشی برای اختصاص اعداد به توابع است؛ بهگونهای که جابهجایی مساحت، حجم و دیگر مفاهیم برآمده از ترکیب دادههای بینهایت کوچک را بهوسیله آن بتوان توصیف کرد. انتگرالگیری یکی از دو عمل مهم در حساب دیفرانسیل و انتگرال است که عمل دیگر آن (عمل معکوس) دیفرانسیلگیری یا همان مشتقگیری است.
محاسبهی مساحت
بهمنظور محاسبه مساحت سطحِ زیر یک نمودار میتوان آن را چند قسمت کرد. برای راحتی کار عرض تمامی این بخشها، یکسان و برابر در نظر گرفته میشود.
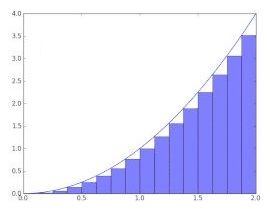

با محاسبه مستطیلهای فرضشده، میتوان مساحت زیر نمودار را به دست آورد. احتمالاً شما نیز متوجه شدهاید که مساحت محاسبهشده با مقدار مدنظر تفاوت خواهد داشت. هر چه ما را کوچکتر در نظر بگیریم، مساحت محاسبهشده بهاین شکل و مساحت شکل مدنظر به یکدیگر نزدیکتر خواهد شد.
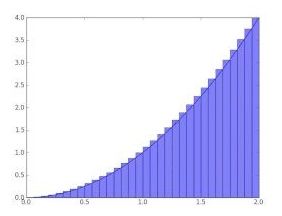

بر همین مبنا، اگر به صفر میل کند (مساحت به بینهایت بخش تقسیم شود)، مساحت مدنظر ما نیز به دست میآید. با محاسبه مساحت بینهایت مستطیل، میتوان سطح زیر یک نمودار را به دست آورد.
انتگرال معین و نامعین
انتگرال بهزبان ساده همان مساحت زیر نمودار است که میخواهیم آن را محاسبه کنیم. انتگرال را بهشکل
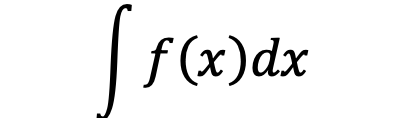
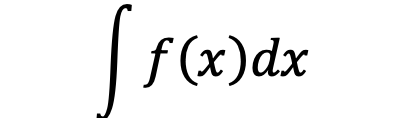
نشان میدهند که علامت آن یک s کشیده است. پس از این نماد تابعی قرار میگیرد که هدف ما محاسبه انتگرال آن است. سپس dx قرار میگیرد که نشاندهندهی عرض هر یک از مستطیلهاست. معادله انتگرالها بهشکل
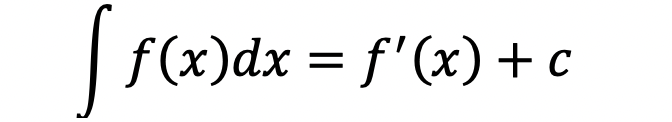
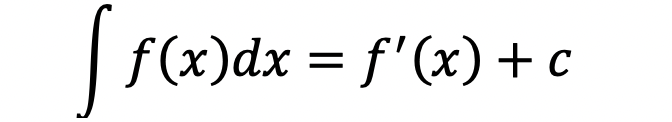
خواهد بود. c یک مقدار ثابت انتگرالی است که نماد تمام اعداد ثابتی است که ممکن بوده با تابع اولبه جمع شده باشند و در زمان مشتقگیری حذف شده باشد. این نمایش از انتگرال نمایش انتگرال نامعین است. در انتگرالهای نامعین حدود تابع انتگرالگیری مشخص نیست و درنتیجه مقدار مساحت به دست نمیآید. درحقیقت به دنبال تابع مساحت هستیم.
اگر بازه انتگرالگیری مشخص باشد، به این نوع انتگرال معین میگوییم که بهشکل
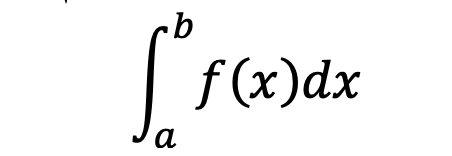
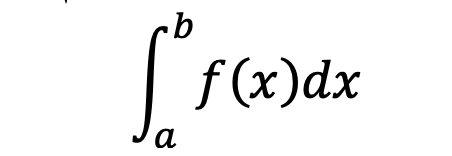
نشان داده میشود. a و b نقاط ابتدا و انتهای تابع هستند.
انتگرال و مشتق
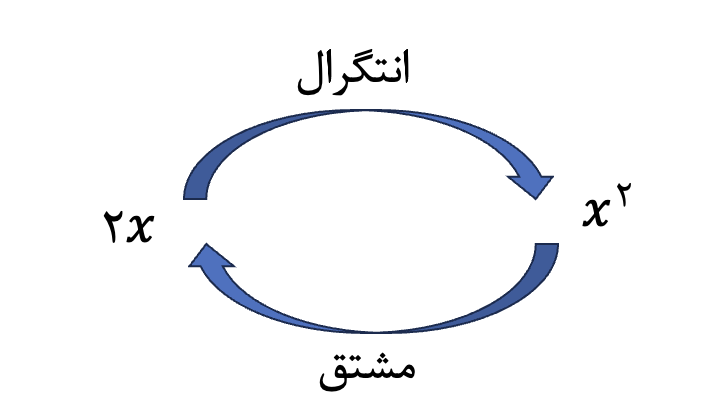

انتگرال و مشتق دو عامل مهم در ریاضیات هستند. درحقیقت برای محاسبه انتگرال لازم است در مرحلهی اول فرمولهای مشتقگیری را بلد باشید؛ زیرا انتگرال عکس مشتقگیری است؛ بنابراین سعی کنید در قدم اول بر فرمولهای مشتقگیری مسلط باشید، زیرا منجر به این میشود که فرمولهای انتگرال را یاد بگیرید.
قواعد انتگرالگیری
باتوجه به اینکه مشتق و انتگرال عکس یکدیگر هستند میتوان با فرمولهای زیر انتگرال بسیاری از توابع را محاسبه کرد:


قوانين انتگرالگیری
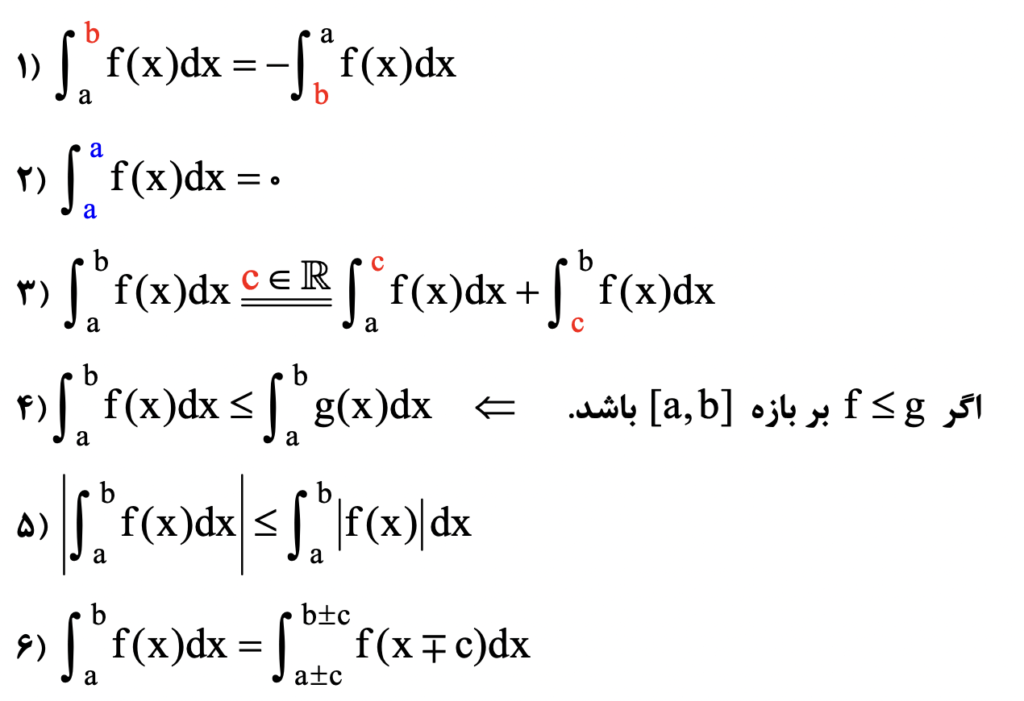
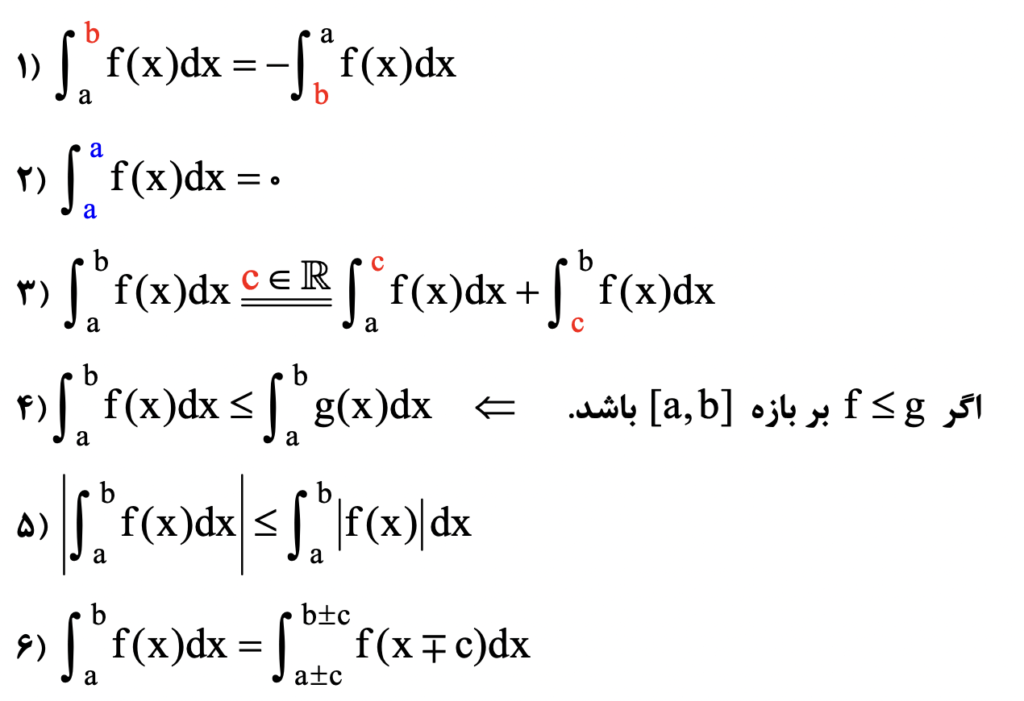
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

