انتگرال خط روی خمهای پارامتری تعریف میشوند. انتگرالهای خط انتگرال مسیر نیز نامیده میشوند. از کاربردهای انتگرال خط میتوان به محاسبه شار و کار انجامشده اشاره کرد. تابعی که باید از آن انتگرال گرفته شود ممکن است در یک میدان اسکالر یا یک میدان برداری باشد. مقدار انتگرال خطی برابر جمع مقادیر میدان روی تمامی نقاط منحنی است و بهوسیله مقدار توابع اسکالر روی منحنی محاسبه میشود. برای آشنایی کامل با انتگرال خط تا پایان این مطلب با ما همراه باشید.
خمهای پارامتری
روی خمهای پارامتریشده انواع مختلفی از انتگرالها تعریف میشود. در ادامه خمها را معرفی می کنیم:
خم باز
هر خم پارامتری تابعی برداری به فرم a(x(t),y(t),z(t)) بوده که a(n) و a(m) در آن به ترتیب نقطه ابتدایی و انتهایی گوییم و جهت خم را از a(n)به a(m) در نظر میگیریم.
خم بسته
خم های بسته نیز مانند خمهای باز به فرم a(x(t),y(t),z(t)) نوشته میشود. در خمهای بسته a(n)=a(m) است.
خم ساده
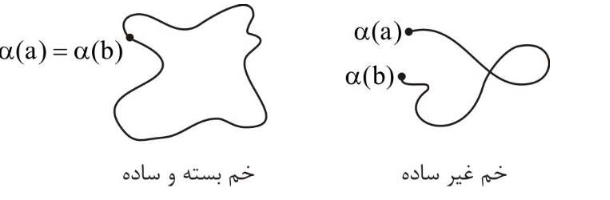
اگر خمی در نقطهای خودش را قطع نکند (مگر در ابتدا و انتها) خم را ساده میگوییم و اگر در نقطهای در میانه خود را قطع کند، خم را غیرساده میگوییم.

خم قطعه قطعه هموار
اگر مشتق a تابعی پیوسته و ناصفر باشد، خم a را هموار مینامیم و اگر خم در نامتناهی نقطه مماس نداشته باشد، آن را ناهموار میگوییم. اگر تعداد نقاط بدون مماس متناهی و شمارا باشد، خم را قطعهقطعه هموار میگوییم.
انواع روشهای انتگرال گیری در ریاضیات عمومی
انتگرال خط نوع اول
برای تابع چندمتغیره
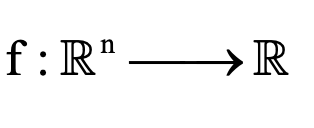
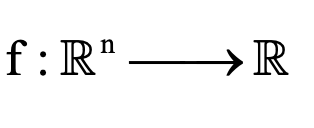
هر انتگرال خط نوع اول به فرم
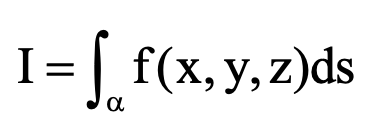
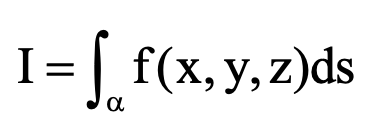
که در آن a یک خم قطعه قطعه هموار روی دامنه است نمایش میدهیم. به ds جز سطح با المان طول قوس میگوییم و برای حالات مختلف داریم:
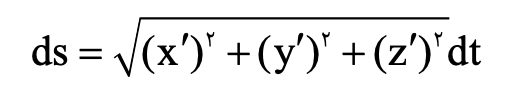
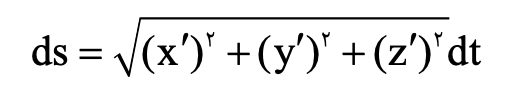
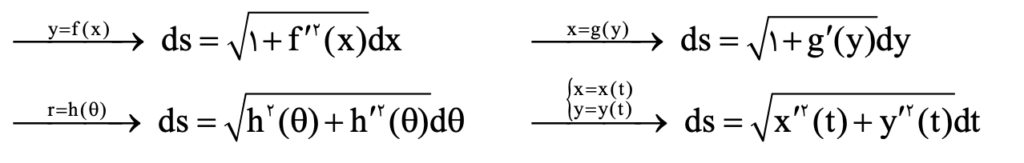
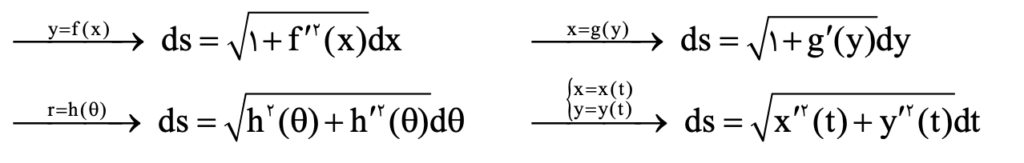
نکات:
- اگر تابع تحت انتگرال برابر ۱ باشد، حاصل انتگرال خط طول قوس خم روی بازه مفروض است.
- اگر تابع تحت انتگرال را به چگالی یک سیم تعبیر کنیم، انتگرال خط همان جرم سیم را می دهد.
- اگر z برحسب x و y باشد و خم در صفحه xoy باشد، در این حالت انتگرال روی خم برابر مساحت سطح خواهد بود.
- هر انتگرال خط خاصیت خطبودن و جمعپذیری دارد و مقدار انتگرال مستقل از نحوه پارامتریکردن خم یا جهت حرکت روی خم است.
انتگرال خط نوع دوم
در نوع اول این انتگرال یک تابع با میدان اسکالر روی خم گرفته میشود. در انتگرال نوع دوم انتگرال یک تابع با میدان برداری روی خم بررسی میشوم.
کار
کار انجامشده توسط نیروی میدان F روی هم a بهاین صورت نشان داده میشود که به آن چرخش میدان F نیز میگویند.
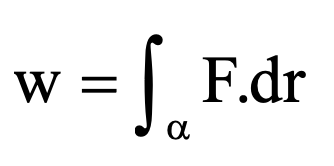
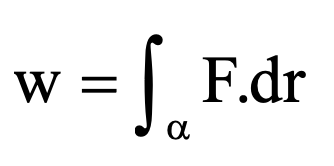
انتگرال روی مرز پارامتری را بهاین صورت حل خواهیم کرد:
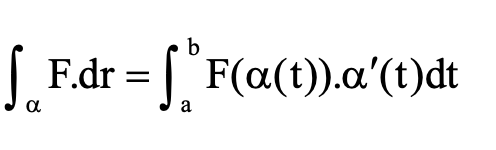
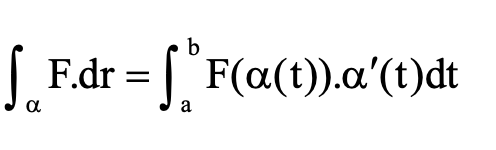
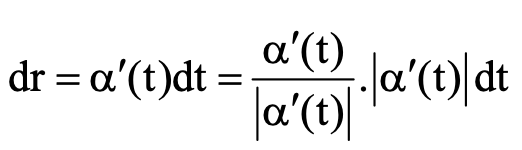
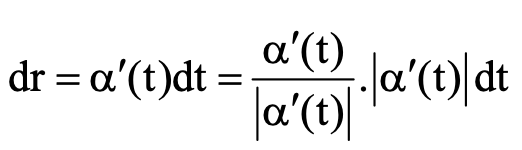
نکات
- انتگرال خط کار خطی است.
- انتگرال کار جمعپذیر است.
- کار انجامشده مستقل از نحوه پارامتریکردن مسیر خم است.
کار انجامشده در خلاف جهت خم قرینه خواهد بود.
میدان پایستار (ابقایی)
از آنجا که کار انجامشده توسط برخی از توابع تنها به ابتدا و انتهای بازه وابستگی دارد و وابسته به مسیر نیست، میتوان روش دیگری برای محاسبه انتگرال کار براساس این میدانها ارائه کرد.
به این دسته توابع پایستار گفته میشود. برای بررسی پایستاری تابع از این روش استفاده میکنیم:
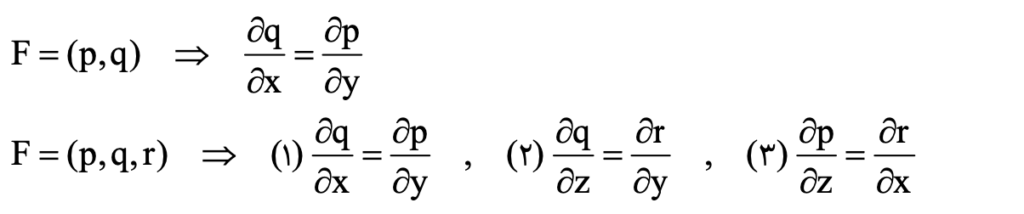
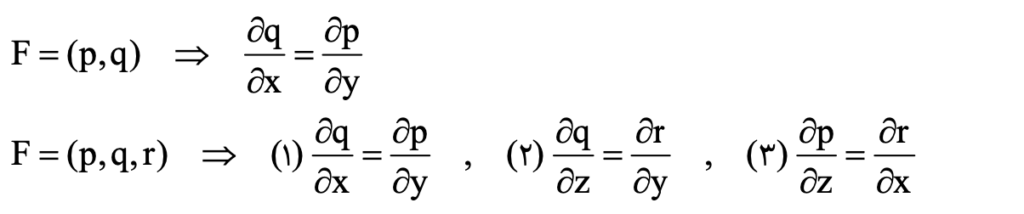
از آنجا که کار انجامشده توسط یک میدان برابر اختلاف پتانسیل میان دو نقطه مدنظر است، برای میدانهای پایستار داریم:
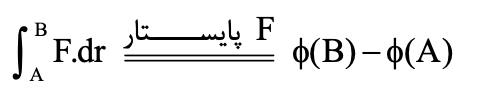
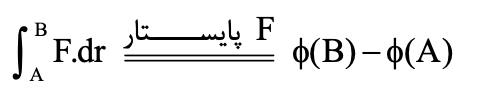
برای محاسبه تابع پتانسیل و جاگذاری نقاط در آن از این فرمول استفاده میکنیم:
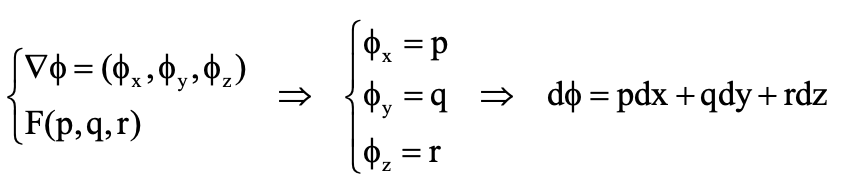
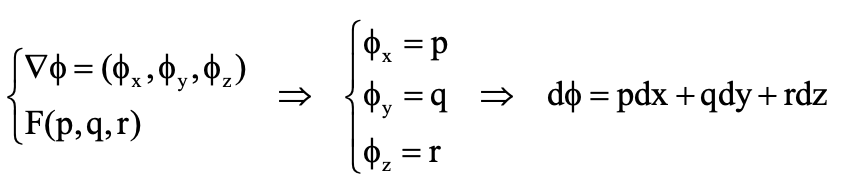
قضیهگرین
این قضیه، ارتباط میان انتگرال خط و انتگرال داخل ناحیه محصور توسط خم بسته را بیان میکند. در این فضیه اگر خم بسته، ساده و قطعه قطعه هموار باشد و ناحیه محصور را داشته باشم برای میدان برداری داریم:
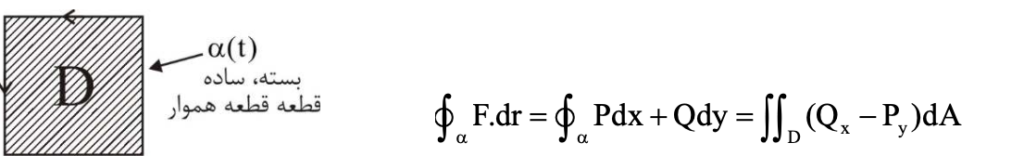
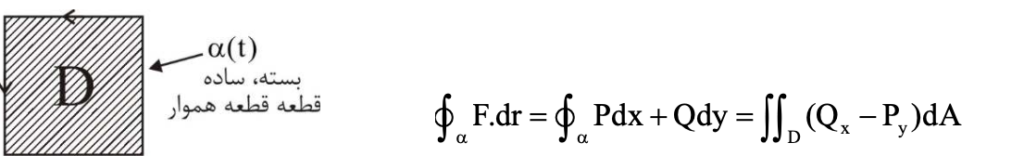
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

