تابع دومتغیرهی f(x,y) را در نظر بگیرید؛ اگر بخواهیم از این تابع انتگرال بگیریم، x ،y یا هردوی آنها متغیر هستند؟ این جا است که مفهوم انتگرال دوگانه مطرح میشود. انتگرالهای دوگانه در مسائل فیزیک و مهندسی کاربرد بسیاری دارند.
انتگرال دوگانه
انتگرال دوگانه معرف حجم زیر تابع است که دو متغیر دارد. اگر D ناحیهای کراندار در فضای دوبعدی باشد و f(x,y) یک تابع پیوسته روی D باشد، انتگرال دو گانه تابع f روی ناحیه D گویند:
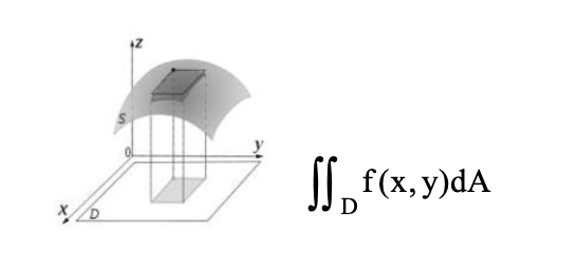

نکتههای انتگرالهای دوگانه


خواص انتگرالهای دوگانه
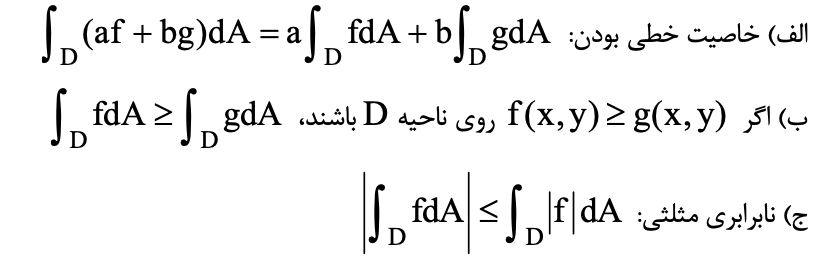
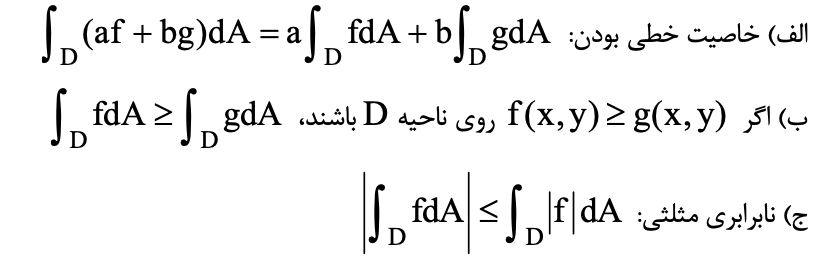
محاسبه انتگرال دوگانه
در انتگرالهای دوگانه از سه روش برای محاسبه استفاده میکنیم:
محاسبه در دستگاه مختصات دکارتی
براساس مفهوم dA که جزئی از یک سطح است و تعبیر dxdy یا dydx دارد، در محاسبه انتگرالهای دوگانه ترتیب المان ها در جایگذاری کرانها اهمیت دارد.
سطح S نسبت به محور منتظم است، هرگاه هر خط به موازات آن محور سطح را حداکثر در دو نقطه قطع کند.


در حالت دکارتی مزیتی که انتگرال چندگانه نسبت به انتگرال ساده دارد این است که گاهی برای محاسبه انتگرال داخلی اگر انتگرالده نسبت به متغیر اول انتگرال دشواری داشته باشد، میتوان با جابهجایی المان انتگرالگیری و تغییر کرانها برحسب این جابهجایی، انتگرال را به فرم ساده تری محاسبه کنیم.
انواع روشهای انتگرال گیری در ریاضیات عمومی
محاسبه در مختصات قطبی
اگر انتگرالگیری در مختصات دکارتی انتگرالهای دوگانه به فرمی باشد که از محاسبه آن در مختصات قطبی دشوارتر باشد، از مختصات قطبی با جایگزینیهای زیر و تغییر کرانها برحسب r و استفاده می کنیم:
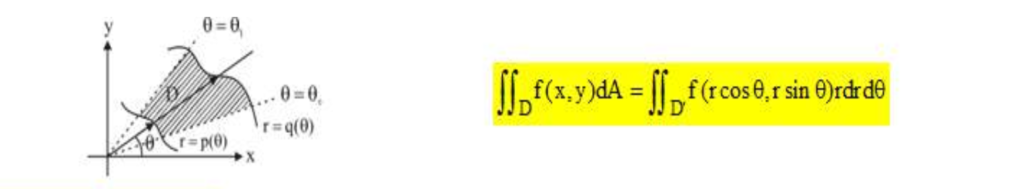
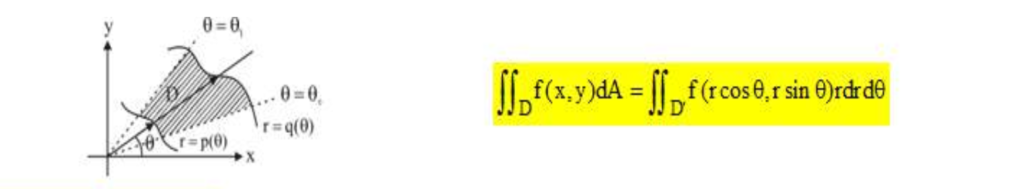
برای مختصات بیضوی نیز با تغییر متغیرهای مرتبط برای محاسبه انتگرال دوگانه می توانیم از این روش استفاده کنیم.
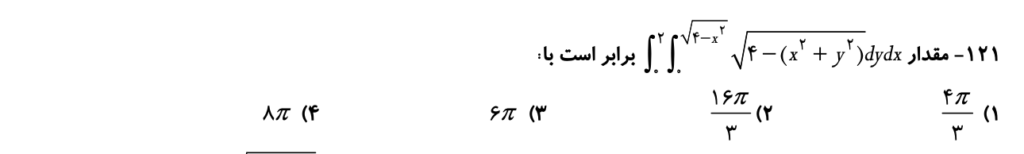
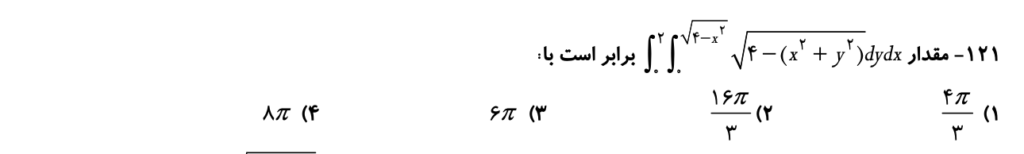


محاسبه با تغییر متغیر
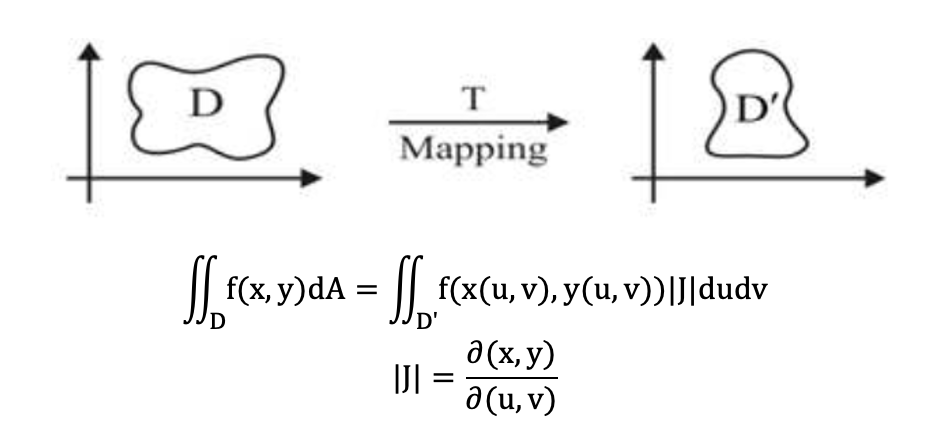
مانند تغییر متغیر در انتگرالهای ساده ریاضی ۱، در انتگرال چندگانه و در اینجا دوگانه تغییر متغیر خاص داریم که در آن بیش از یک عبارت را تغییر داده و بهجای دیفرانسیل، ماتریس بردار گرادیان این تبدیلات را به شکلی که در ادامه نشان دادهایم بهعنوان ضریب خواهیم داشت. با تغییر متغیر از یک ناحیه نگاشتی به ناحیه جدید داریم و انتگرال ناحیه جدید بهاین صورت خواهد بود:

نمونه سوال
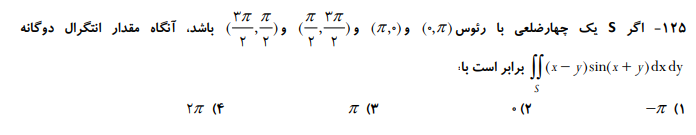
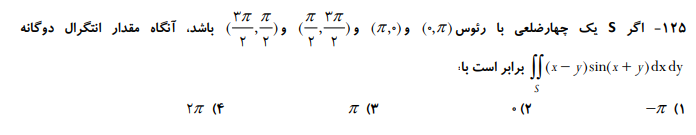


کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

