انتگرال سطح یا Surface integral در ریاضیات یک انتگرال معین است که روی یک سطح گرفته میشود. با داشتن یک سطح، انتگرالگیری میتواند روی میدانهای برداری آن (توابعی که مقدار آنها یک بردار اقلیدسی است) انجام گیرد. در این مطلب با انتگرال سطح و انواع آن بهصورت کامل آشنا میشوید.
انتگرال سطح
در اصل ایده انتگرال روی سطح نیز مشابه با انتگرال دوگانه است. تنها تفاوت این است که ناحیه انتگرالگیری روی صفحه سهبعدی قرار میگیرد؛ بههمین دلیل، نمادهای استفادهشده برای انتگرال سطحی بسیار مشابه با انتگرال دوگانه است. درحقیقت انتگرال سطحی را بهاین صورت نمایش میدهند:
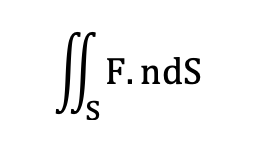
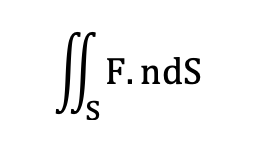
انتگرالگیری روی سطوح در فیزیک و بهویژه در نظریهٔ کلاسیک الکترومغناطیس کاربرد دارد. انتگرال سطحی بهعنوان یکی از ابزارهای مهم در محاسبات مساحت سطحی در فضا و در حوزههایی مانند گرافیک کامپیوتری، فیزیک و مهندسی نیز استفاده میشود.
میزان انتگرال سطحی مساحت یک سطح سهبعدی را به ما نشان خواهد داد.
برای آشنایی با انتگرال دوگانه این مطلب را مطالعه کنید:
انتگرال سطحی توابع برداری یک مفهوم ریاضی است که به محاسبه مساحت سطحی در فضا میپردازد. در اینجا توابع برداری معمولاً توسط یک بردار توابع f(u,v)=(x(v,v),y(u,v),z(u,v))توصیف میشوند که در آن (u) و (v) پارامترهای دوبعدی هستند.
انتگرال سطحی تابع برداری روی دامنهٔ دوبعدی (D) را میتوان با استفاده از فرمول انتگرال سطحی محاسبه کرد.
روی هر سطح رویه دو نوع انتگرال سطحی قابلتعریف است.
انتگرال سطحی نوع اول
نوعی انتگرال سطحی که روی سطح منحنی شکل و تابعی اسکالر گفته میشود. بر این اساس هر انتگرال دوگانه
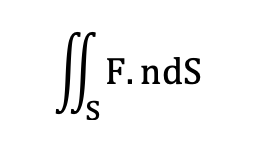
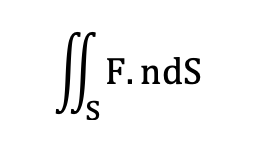
که در آن S بیانگر سطح یک رویه و dS المان مساحت روی S است به انتگرال سطحی نوع اول معرفی شده است.


انتگرال سطحی نوع دوم
برای میدان برداری پیوسته شار برونسوی میدان F در جهت بردار n که n بردار یکه قائم به خم قطعهقطعه هموار a است بهاین شکل است: ادمخ هر سیهرا خم صبا هص ثادثصخه بض صثا صث با خصث اب صخا صث هاخ صاب
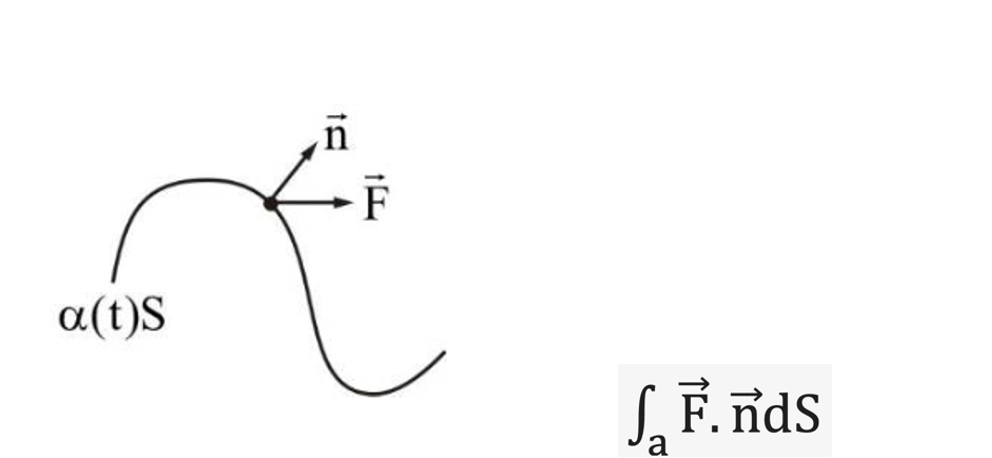



انتگرال سطح توابع برداری یک مفهوم ریاضی است که به محاسبه مساحت انتگرال سطح توابع برداری یک مفهوم ریاضی است
قضیه دیورژانس
اگر S سطحی قطعهقطعه هموار و بسته باشد که ناحیه w را محصور کند و n بردار یکه قائم رو به خارج سطح S در هر نقطه باشد، اگر میدان
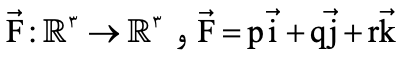
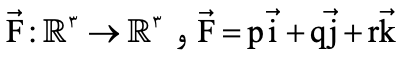
وجود داشته باشد که
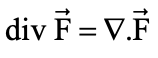
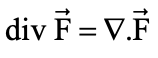
در ناحیه W پیوسته باشد، برای محاسبه شار با استفاده از قضیه دیورژانس داریم:
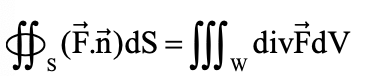
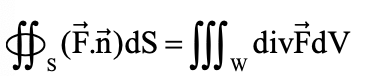
بر این اساس شار خروجی از سطح S معادل شار داخل ناحیه W خواهد بود.
نمونه سوال
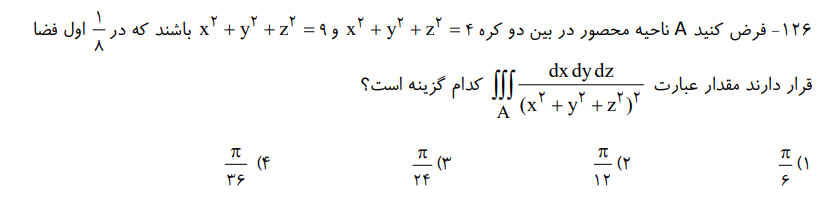
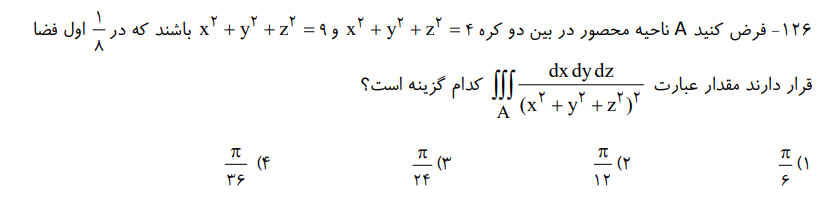


کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

