موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد. ضریب این درس در کنکور رشته مدیریت کسب و کار ۲ است و اهمیت آن بر داوطلبان پوشیده نیست. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید.
اهمیت درس ریاضی عمومی ۱ و ۲
ریاضی عمومی ۱ و ۲ از دروس پایهای رشتههای مختلف است. اهمیت این درس به سه دلیل عمده بازمیگردد؛ اولین دلیل این است که این درس جزو سرفصلهای امتحانی بسیار مهم رشتههای مختلف است. دلیل دوم به محتوای ارائهشده در این درس بازمیگردد. محتوای این درس بهقدری مهم است که آشنایی با مفاهیم آن به درک مفاهیم سایر درسهای دورهی کارشناسی و سایر مواد آزمون کارشناسیارشد کمک شایانی میکند. سومین دلیل اهمیت این درس و کلاس آنلاین ریاضی عمومی ۱ و ۲ نوع نگاهی است که در حل مسائل این درس وجود دارد؛ این نگاه عاملی اساسی در شکلگیری تفکر انتقادی در حل مسائل است.
طرز اصولی مطالعه ریاضی عمومی ۱ و ۲ چگونه است؟
در این سری از مقالات برخی از موضوعات مهم دروس را با نگاه آموزشی و به صورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید.
تابع به زبان ساده
تابع در ریاضی به مجموعهای از قوانین و روابطی گفته میشود که برای دادههای مختلف ورودی، خروجی مشخصی تولید میکند. به عبارت دیگر، تابع یک نوع محاسبه است که برای هر ورودی، یک خروجی مشخص دارد. به عنوان مثال، تابع جمع دو عدد، هر دو عدد را ورودی گرفته و خروجی آن جمع این دو عدد است. در ریاضیات، توابع با نماد f(x) نشان داده میشوند که در آن x ورودی تابع است و f(x) خروجی آن است.
معرفی انواع تابع
براساس فرم معادله توابع، دستههای مختلفی از توابع را در ریاضیات خواهیم داشت. در ادامه این توابع را معرفی خواهیم کرد:
توابع همانی
در تابع همانی مقدار ورودی به عنوان خروجی باز میگردد. به عبارت دیگر، در تابع همانی مقدار ورودی و خروجی باهم برابرند. یک نمایش زوج مرتبی از تابع به صورت زیر است:
R={(1,1)(2,2)(3,3)}
مهمترین خواص تابع همانی عبارت هستند از:
- تابع همانی، یک تابع خطی با مقادیر حقیقی است.
- شیب نمودار تابع همانی نسبت به محورهای x و y برابر با ۴۵ درجه است.
- تابع همانی و وارون آن، با یکدیگر برابر بوده و دارای نمودار یکسان هستند.
توابع جبری
توابع جبری یا چندجملهای از پرکاربردترین انواع توابع در ریاضی هستند که به فرم زیر نوشته میشوند.
در توابع جبری بزرگترین توان x، درجه تابع را مشخص میکند. این توابع خود انواع مختلفی دارند که ساده ترین آنها، تابع ثابت است. توابع با درجه یک، توابع خطی نامیده میشوند. در حقیقت تابع همانی، تابع جبری با درجه یک است.
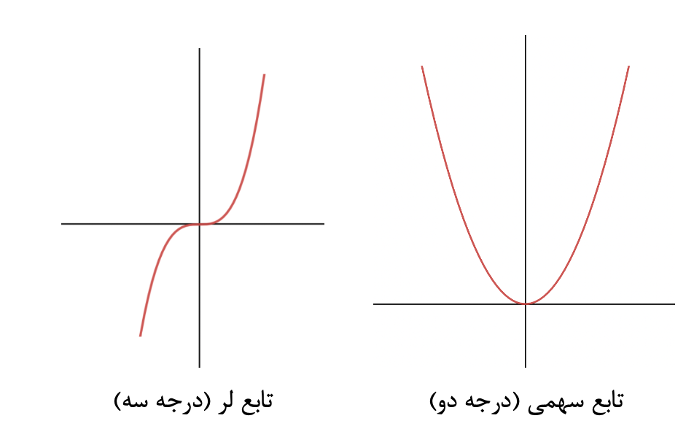
توابع با درجه دو، سهمی و توابع با درجه سه، به خاطر شکلشان لر نامیده میشوند.

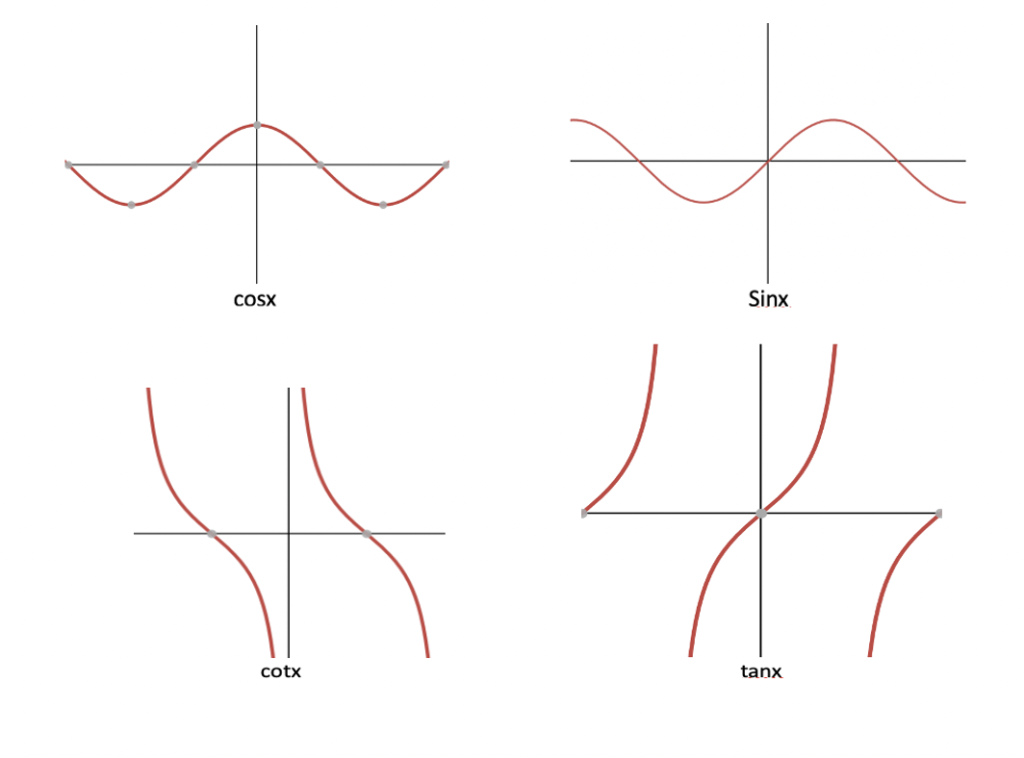
توابع مثلثاتی
در ریاضیات، منظور از توابع مثلثاتی شش تابع سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت است. این توابع رابطهٔ میان زاویهها و ضلعهای یک مثلث قائمالزاویه را نشان میدهند و به همین دلیل توابع مثلثاتی نامیده میشوند. دامنه توابع sinx و cosx، R و برد آنها [۱,۱-] میباشد.

تابع قدرمطلق
تابع قدر مطلق تابعی است که علامت خروجی آن، به مثبت یا منفی بودن ورودی بستگی ندارد. خروجی تابع قدر مطلق، همیشه غیرمنفی (۰ یا مثبت) است. در توابع قدر مطلق، مقدار خروجی، به مقدار ورودی بستگی دارد. با این وجود، علامت خروجی، همواره غیر منفی است. به عنوان مثال، تابع زیر را در نظر بگیرید:
F(x)=|x|
اگر علامت ورودی x مثبت یا مقدار x برابر با ۰ باشد، f(x)برابر با x خواهد بود. در صورت منفی بودن x، مقدار f(x) برابر با x- میشود.
تابع علامت
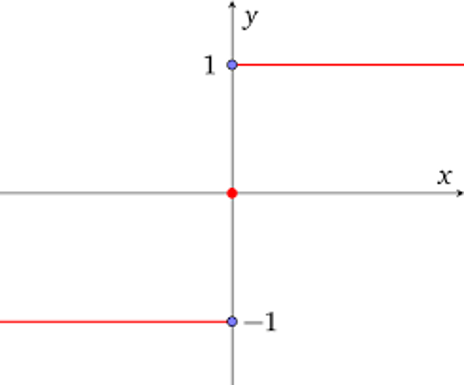
تابع علامت یکی از انواع تابع است که در ورودی، اعداد مثبت را با یک و اعداد منفی را با منفی یک برمیگرداند. به عنوان مثال، تابع علامت برای عدد ۵ برابر ۱ و برای عدد -۳ برابر -۱ خواهد بود. نماد تابع علامت به صورت sgn(x) نمایش داده میشود.
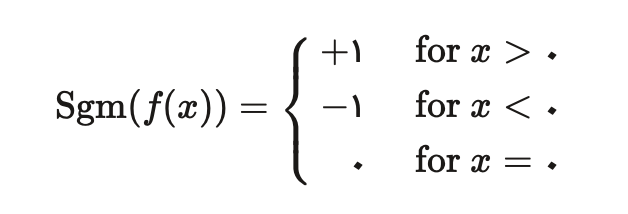
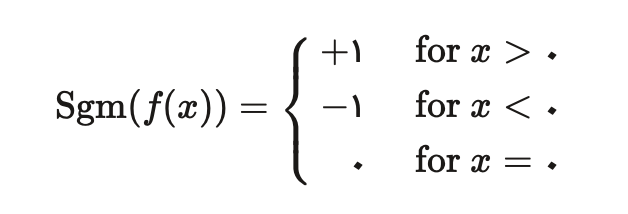
نمودار تابع علامت به صورت زیر است:

تابع لگاریتمی
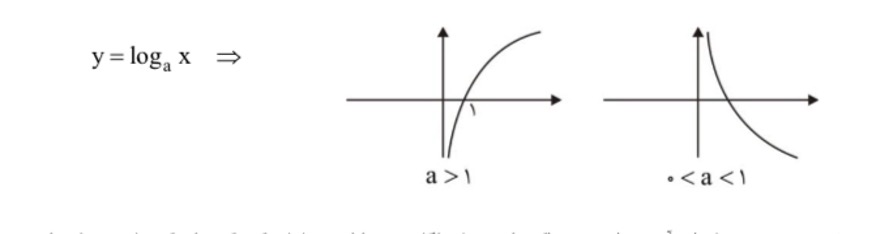
تابع لگاریتمی، تابعی است که برای یک عدد مثبت x، لگاریتم نسبی آن به اساس a را برمیگرداند. به صورت ریاضی، تابع لگاریتمی به صورت زیر تعریف میشود:
log_a(x) = y
که در آن، a اساس لگاریتم و x عدد مثبت و y مقدار لگاریتم نسبی است. به عنوان مثال، log_10(100) برابر با 2 است؛ به این معنی که ۱۰ به توان ۲ برابر با ۱۰۰ است.

تابع نمایی
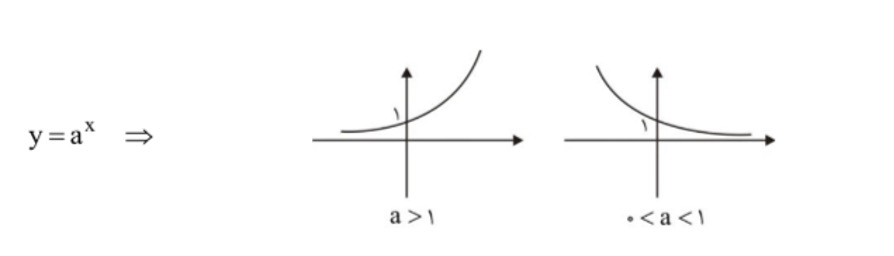
تابع نمایی، تابعی است که به صورت توانی از یک عدد ثابت e (نمادی برای عدد اویلر) تعریف میشود. به صورت ریاضی، تابع نمایی به صورت زیر تعریف میشود:
f(x) = e^x
در اینجا، e عدد اویلر و x پارامتر ورودی تابع است. مقدار خروجی تابع نمایی برای هر مقدار x، برابر با e به توان x است. به عنوان مثال، e^2 برابر با 7.389 است.

کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

