انواع مشتق توابع در ریاضیات عمومی چیست؟ موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد. ضریب این درس در کنکور رشته مدیریت کسب و کار ۲ است و اهمیت آن بر داوطلبان پوشیده نیست. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید. برای مشتقگیری باید انواع توابع مشتق را بشناسید. انواع مشتق را در ادامه معرفی کردهایم.
اهمیت درس ریاضی عمومی ۱ و ۲
ریاضی عمومی ۱ و ۲ از دروس پایهای رشتههای مختلف است. اهمیت این درس به سه دلیل عمده بازمیگردد؛ اولین دلیل این است که این درس جزو سرفصلهای امتحانی بسیار مهم رشتههای مختلف است. دلیل دوم به محتوای ارائهشده در این درس بازمیگردد. محتوای این درس بهقدری مهم است که آشنایی با مفاهیم آن به درک مفاهیم سایر درسهای دورهی کارشناسی و سایر مواد آزمون کارشناسیارشد کمک شایانی میکند. سومین دلیل اهمیت این درس و کلاس آنلاین ریاضی عمومی ۱ و ۲ نوع نگاهی است که در حل مسائل این درس وجود دارد؛ این نگاه عاملی اساسی در شکلگیری تفکر انتقادی در حل مسائل است.
در این وبلاگ کافهتدریس برخی از موضوعهای مهم درسها را با نگاه آموزشی و به صورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید.
مشتق بهزبان ساده
حد نسبت تغییرات تابع به متغیر زمانی را که بسیار کوچک شود به میزانی که به صفر میل کند تابع گوییم. مشتق را با یا نشان میدهیم.
درواقع مشتق همان شیب خط مماس در نقطهی مدنظر است.
حد در ریاضیات عمومی ۱ و ۲ چیست؟
انواع مشتق توابع
مشتقها باتوجه به نوع تابعی که از آن مشتقگیری میکنیم با یکدیگر متفاوت هستند و روش محاسبه متفاوت دارند. در ادامه مطلب انواع مشتق توابع و هر یک از توابع را بررسی میکنیم.
توابع متعالی
توابع متعالی توابعی هستند که یک تابع به توان تابعی دیگر رسیده باشد، بهعبارتی متغیر به توان متغیر است. برای توان سادهترین راهی که میتوان استفاده کرد خاصیت توانشکنی لگاریتم است. برای اینکه از این دسته از توابع بتوانیم مشتق بگیریم،
- از طرفین ln میگیریم؛
- از دو طرف عبارت بهدستآمده مشتق میگیریم؛
- دو طرف عبارت را مجددا به توان e میرسانیم.
توابع قدر مطلق و براکتی
در اکثر زمانهایی که با توابع قدر مطلقی یا براکتی مواجه میشویم، قدرمطلق را تعیین علامت و براکت را تعیین مقدار میکنیم. در مشتق تیز از این قاعده مستثنى نیستیم. در این توابع ابتدا ریشه درون عبارت را یافته و تابع را به قبل و بعد ریشه میشکنیم. در این حالت یک تابع چندضابطهای خواهیم داشت که مشتق هر یک را می توانیم در بازه یا در نقطه مدنظر خود بیابیم.
در برخی از حالات که عدد مشتق ریشه عبارت نیست نیاز به بهدستآوردن تابع نداریم و تنها میتوانیم تعیین مقدار یا تعیین علامت کنیم و مشتق را به دست آوریم.
توابع مرکب
توابع مرکب توابعی هستند که یک تابع در دل یک تابع دیگر قرار گرفته است توابعی مانند fog=f(g(x)) از این دسته از توابع هستند. در این توابع باید هم مشتق کل عبارت و هم مشتق تابع درون آن را به دست آوریم. بهعبارتی:
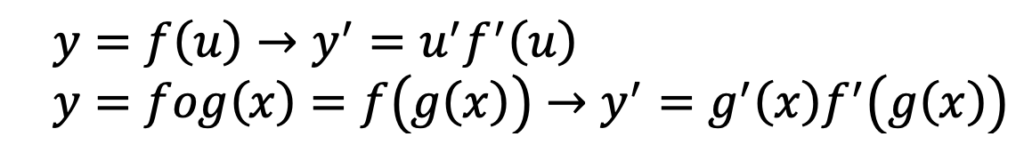
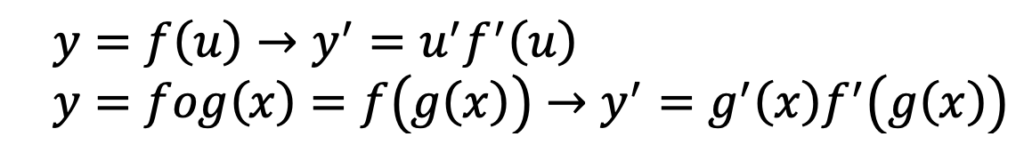
توابع انتگرالی
انتگرال عملگری است که عکس دیفرانسیل عمل میکند. زمانی که انتگرال روی دیفرانسیل تابع اعمال میشود، تابع اولیه برگردانده میشود. انتگرالهایی را که در آن حداقل یکی از کرانها متغیر باشد تابع انتگرالی می نامیم. برای مشتقگیری از این توابع، از قضیه اول بنیادی انتگرال استفاده میکنیم.
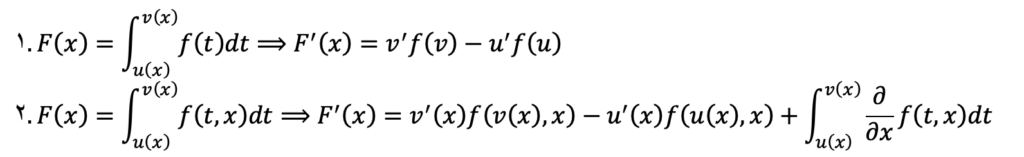
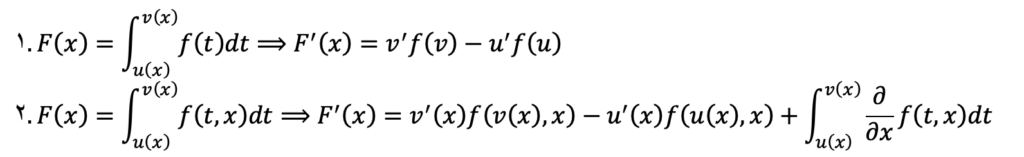
نمونه سوال
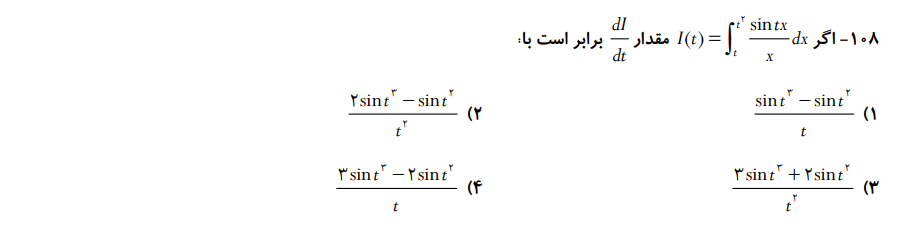
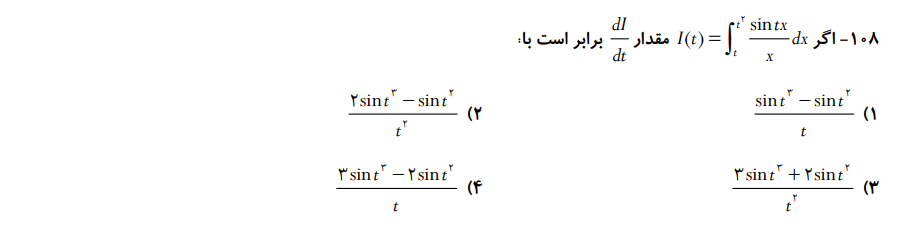
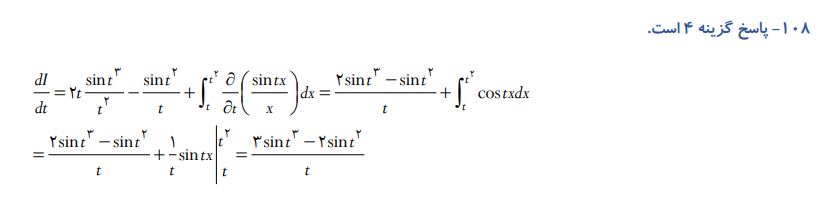
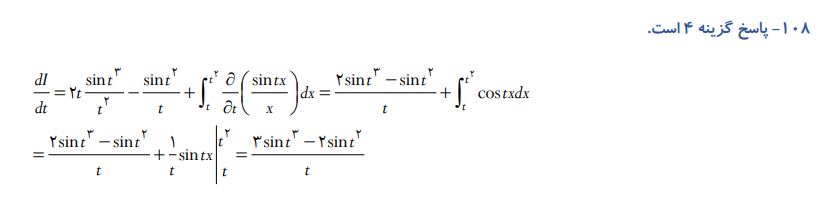
تابع تابع
اگر y تابعی برحسب u و خود u نیز تابعی برحسب x باشد، به آن تابع یا قاعده زنجیرهای گویند. در این صورت برای تعیین مشتق y نسبت به x داریم:
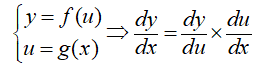
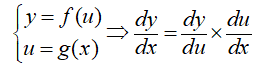
تابع ضمنی و پارامتری
توابع ضمنی توابعی هستند که متغیرهای مستقل و وابسته آن بهصورتی باهم ترکیب شدهاند که امکان نوشتن یکی برحسب دیگری وجود ندارد. برای محاسبه این توابع از قرینه و عکس توابع نسبت به متغیرهای وابسته و مستقل استفاده میکنیم.
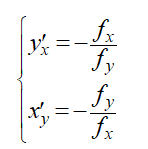
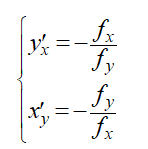
برای توابع پارامتری که x و y به طور غیرمستقیم و از طریق پارامتر سومی باهم ارتباط دارند، بهطور جداگانه از هر یک از متغیرها نسبت به متغیر سوم مشتقگیری میکنیم:
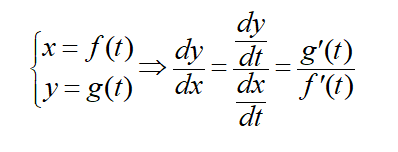
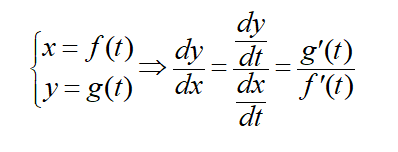
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

