موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد. ضریب این درس در کنکور رشته مدیریت کسب و کار ۲ است و اهمیت آن بر داوطلبان پوشیده نیست. در بسیاری دیگر از رشتهها هم این درس ضریب بالایی دارد. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید. قضایای انتگرالگیری معین از سرفصلهای بخش انتگرال است.
اهمیت درس ریاضی عمومی ۱ و ۲
ریاضی عمومی ۱ و ۲ از دروس اصلی رشتههای مختلف است. اهمیت این درس به دلیل این است که جزو سرفصلهای امتحانی رشتههای مختلف است. محتوای این درس و آشنایی با مفاهیم آن به درک مفاهیم سایر درسهای دورهی کارشناسی و سایر مواد آزمون کارشناسیارشد کمک میکند.
طرز اصولی مطالعه ریاضی عمومی ۱ و ۲ چگونه است؟
در این سری از مقالات برخی از موضوعات مهم دروس را با نگاه آموزشی و به صورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید. قضایای انتگرالگیری یکی از این موضوعات مهم است.
انتگرال
انتگرال، روشی برای اختصاص اعداد به توابع است؛ به گونهای که جابهجایی مساحت، حجم و دیگر مفاهیم برآمده از ترکیب دادههای بینهایت کوچک را به وسیله آن بتوان توصیف کرد. انتگرالگیری یکی از دو عمل مهم در حساب دیفرانسیل و انتگرال است.
قضایای انتگرالگیری معین
در انتگرالها، دو نوع انتگرال معین و نامعین داریم. قضایای انتگرالگیری معین خاصی وجود دارد که برای محاسبه راحتتر انتگرالها از آنها استفاده میشود. انتگرالهای معین بازه ابتدا و انتهای آن مشخص است.
قضیه اول: انتگرالهای توابع زوج و فرد در بازه متقارن
اولین قضيه در قضایای انتگرالگیری معین انتگرال توابع زوج و فرد است. اگر بازه ابتدا و انتهایی انتگرال مشخص شده متقارن باشد، باتوجه به اینکه تابع تحت انتگرال زوج باشد یا فرد مقادیر انتگرال متفاوت خواهد بود.
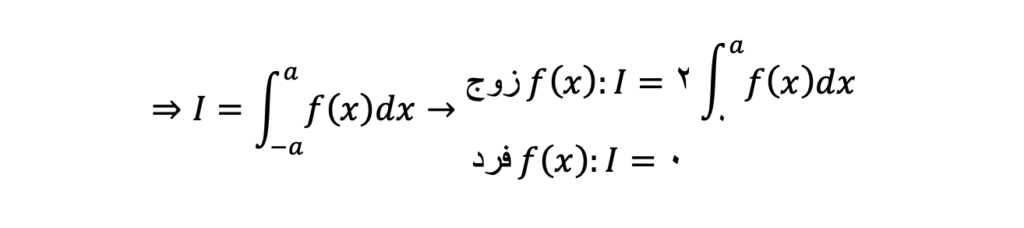
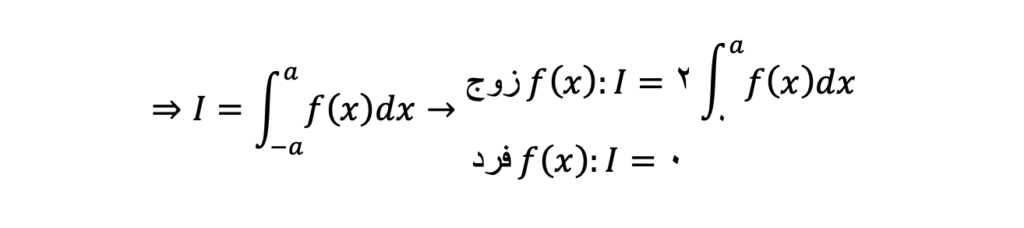
انتگرال براکت و قدر مطلق
در انتگرالهای براکتی و قدرمطلقی ممکن است بازه متقارن داشته باشیم اما محدودیت توابع در این بازه باشد. در این انتگرالها باید نقاط محدودیت را محاسبه کرده و در فواصل بدست آمده آنها را تعیین وضعیت کنیم. برای اینکار کافیست قدرمطلق را اطراف ریشههای عبارت درون آن تعیین علامت و براکت را در مقادیری که صحیح میشود تعیین مقدار میکنیم. و انتگرال را اطراف آن میشکنیم.
قضیه دوم: حد مجموع ریمان
در برخی از مواقع شما با حد مجموع یکسری از توابع با مقدار محدود روبرو میشوید. در این مواقع با اینکه ممکن است به نظر نرسد اما در واقع با انتگرال مواجه هستیم. برای محاسبه اینگونه از توابع میتوانیم به شکل زیر عمل کنیم:
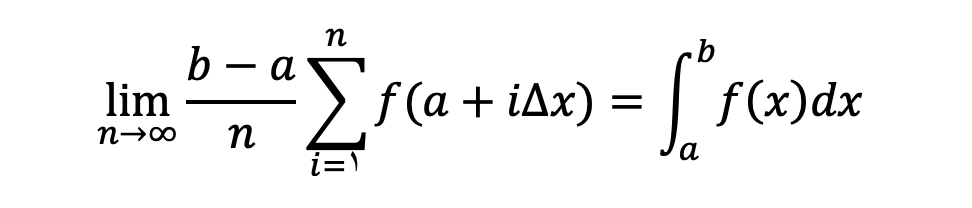
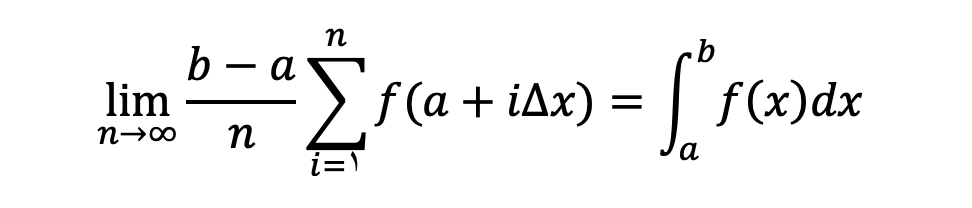
با محاسبه انتگرال به دست آمده در حقیقت مجموع دنباله خواسته شده به دست میآید.
نمونه سوال
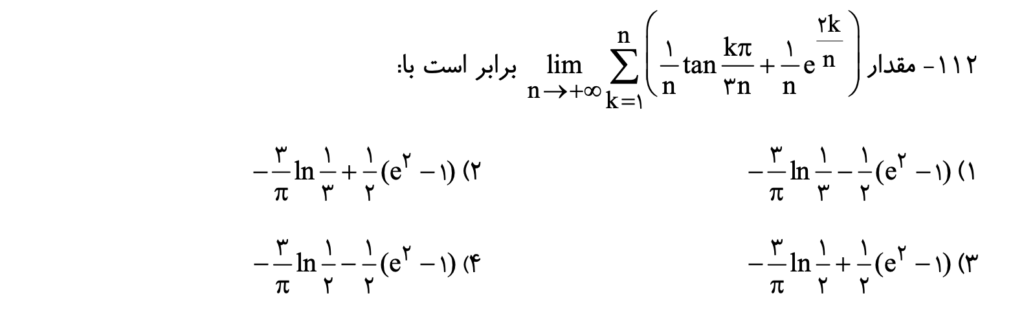
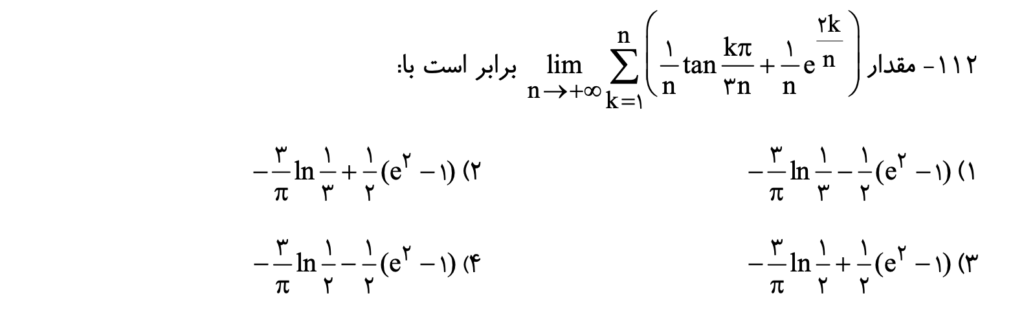


قضیه سوم: مقدار میانگین
اگر تابع y=f(x) بر بازه [a,b] انتگرالپذیر باشد، در این صورت باتوجه به قضایای انتگرالگیری ، مقدار میانگین تابع در نقطه c عضو این بازه برابر است با:
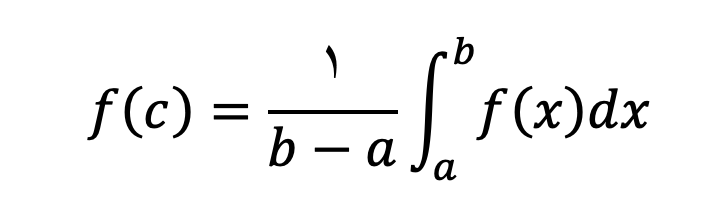
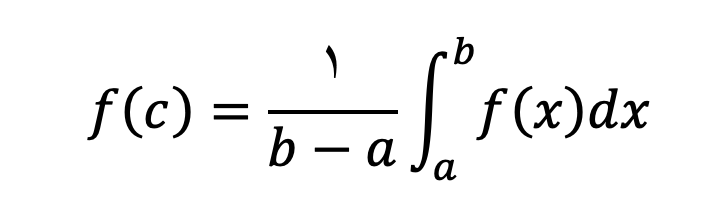
باتوجه به رابطه بالا اگر مینیمم و ماکزیمم تابع را داشته باشیم حدود انتگرال تابع را میتوانیم بدست آوریم.
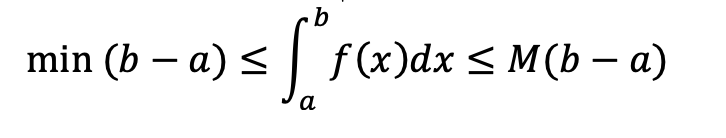
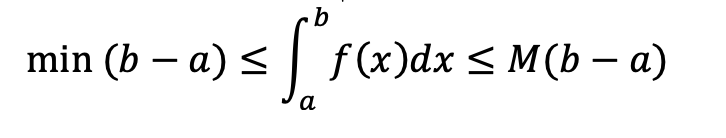
قضیه چهارم: انتگرال مثلثاتی
برای انتگرالهایی که تابع تحت انتگرال آنها مثلثاتی باشد، قضایای انتگرالگیری زیر برقرار است:
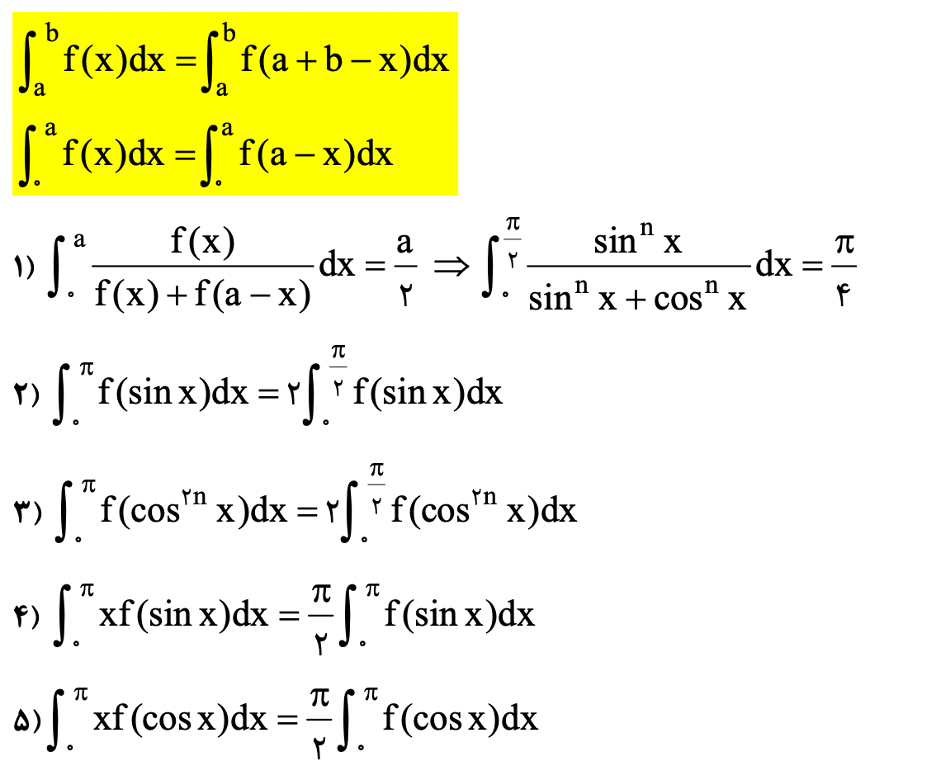
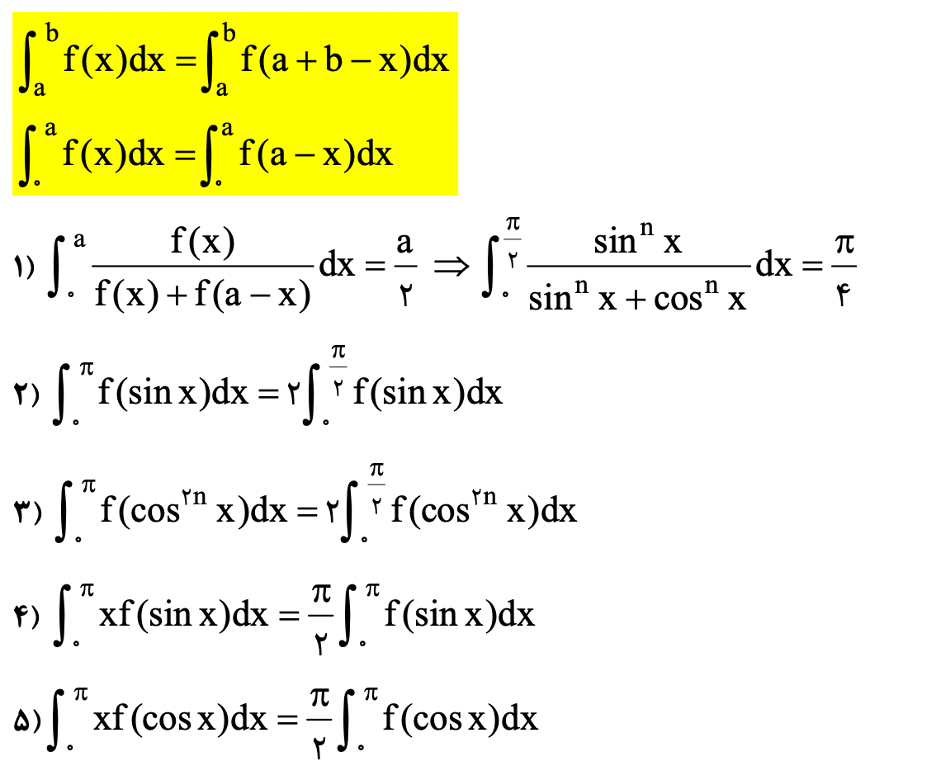
قضیه پنجم: انتگرال معین توابع متناوب
در توابع متناوب قضایای انتگرالگیری بدون صورت است که اگر تابع متناوب و با دوره تناوب T باشد آنگاه اگر بازه انتگرال مضربی از T باشد آنگاه مضرب در یک بازه انتگرال ضرب خواهد شد و مقدار انتگرال در هریک از تناوبهای آن برابر خواهد بود. مقدار توابع sin و cos که متناوب هستند در یک دوره تناوب صفر خواهد بود.
قضیه ششم: انتگرال تابع معکوس
اگر تابع f تابعی پیوسته با مشتقات پیوسته و اکیدا صعودی روی بازه [a,b] باشد. باتوجه به قضایای انتگرالگیری حاصل مجموع دو انتگرال تابع و معکوسش از رابطه زیر پیروی میکند:
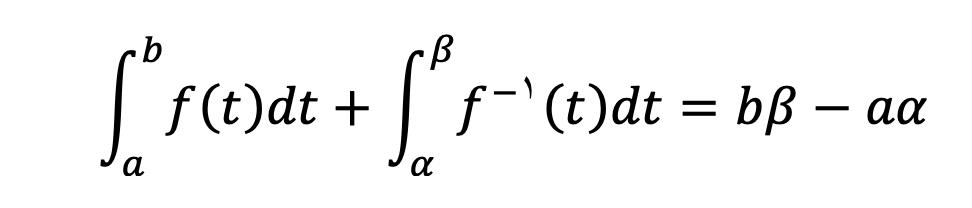
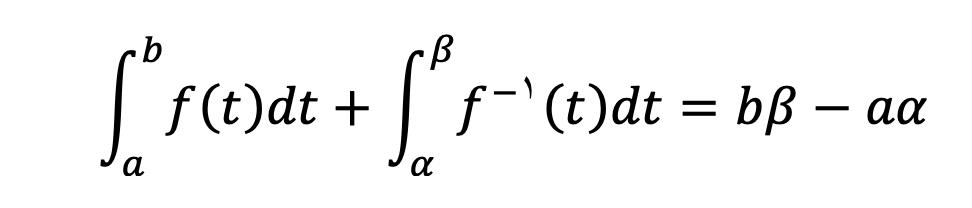
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

