چقدر با ماتریس و قوانین آن در ریاضی عمومی آشنا هستید؟ یکی از مفاهیم مهم در دنیای ریاضی ماتریسها هستند که امروزه در سراسر زندگی کاربردهای گوناگونی دارد. بهصورت کلی ماتریس یک ساختار مستطیلی است که اعداد و عبارتهایی در آن قرار میگیرند و یک حالت را به وجود میآورند. در این مطلب ماتریس و قوانین آن در ریاضی عمومی را توضیح دادهایم.
ماتریس و قوانین آن در ریاضی عمومی
ماتریسها یک آرایش مستطیلی (یا آرایه) از اعداد هستند که بهوسیله یک براکت محصور شده است. هر عدد در این آرایش عنصری از ماتریس نامیده می شود که به آن درایه میگویند.


ماتریسی مانند شکل بالا m سطر و n ستون را شامل است و m.n تا درایه دارد.
مرتبه ماتریس
به تعداد سطرها و ستونهای ماتریسها که بهصورت (ستون×سطر) نوشته میشود مرتبه آن می گوییم. ماتریسی که تنها یک سطر داشته باشد، ماتریسسطری و ماتریسی که تنها یک ستون داشته باشد، ستونی نامیده میشود. البته ماتریسهایی بهشکل تهی هم داریم که ماتریسی است که هیچ درایهای ندارد. به ماتریسی که تعداد سطرها و ستونهایش برابر باشند ماتریس مربعی گفته میشود.
جمع و تفریق ماتریسها
برای جمع دو ماتریس اعداد هم مرتبه آنها را با هم جمع کنید:
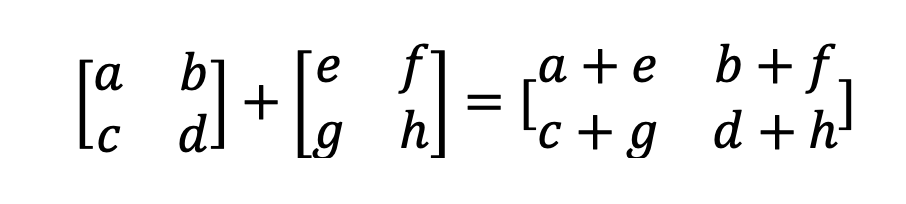
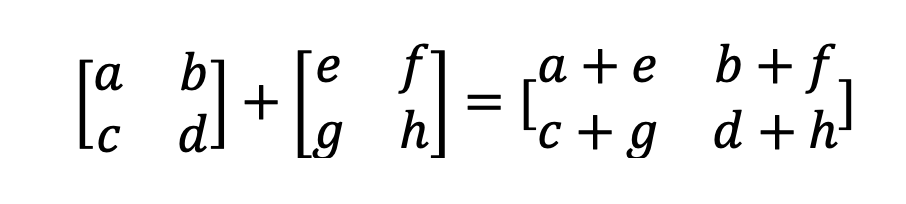
تفریق ماتریسها نیز بهاین شکل است با این تفاوت که اعداد هم مرتبه از هم کم خواهند شد.
ضرب ماتریسها
در ضرب ماتریسها اگر عدد در ماتریس ضرب شده باشد، آن عدد در تکتک درایهها ضرب خواهد شد و نتیجه در ماتریسی جدید به دست خواهد آمد. اگر ضرب دو ماتریس را در یکدیگر داشته باشیم، باید اعداد ستونهای ماتریس سمت چپ با تعداد سطرهای ماتریسی که در سمت راست است برابر باشد. مثالی از ضرب ماتریسها را در زیر میبینید:
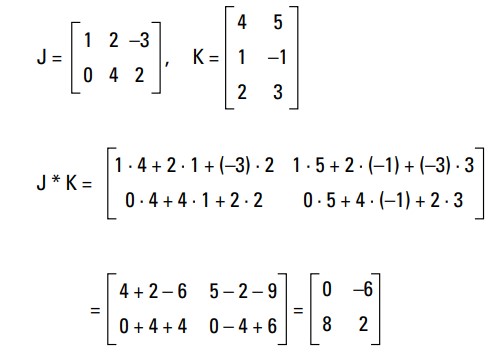
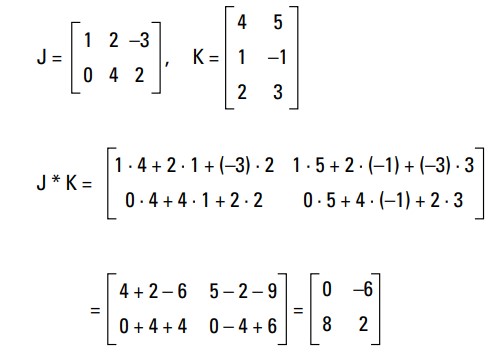
در ضرب ماتریسها درایه اول ماتریسجواب، از ضرب سطر اول ماتریساول در ستون اول ماتریسدوم به دست میآید.
دترمینان ماتریس
برای هر ماتریسمربعی عدد منحصربهفردی وجود دارد که ویژگی آن است و به آن دترمینان گفته میشود. دترمینان ماتریس A را با |A| یا det(A) نمایش میدهند.
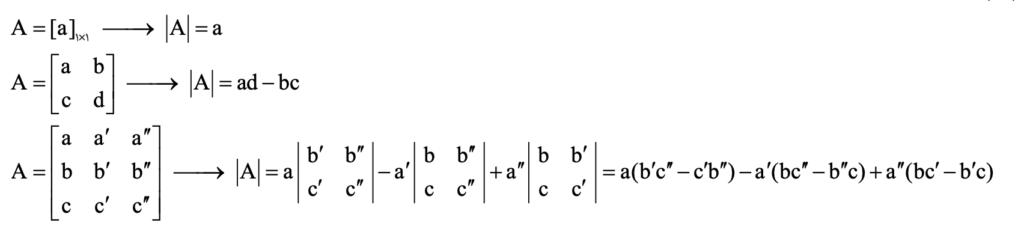
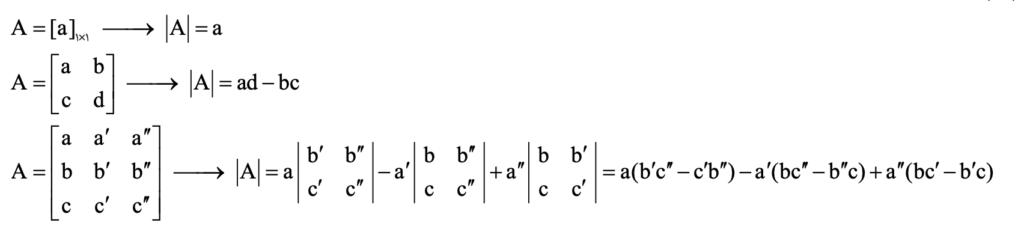
در ماتریسی که سطر یا ستونی صفر باشد یا دو یا چند سطر یا ستون ضریب یکدیگر باشند، دترمینان ماتریس صفر است.
ترانهاده
برای یافتن «ترانهاده» (Transpose)، جای سطرها و ستونها را عوض میکنیم. از حرف «T» در سمت بالا و راست ماتریس، بهعنوان نماد ترانهاده استفاده میشود.
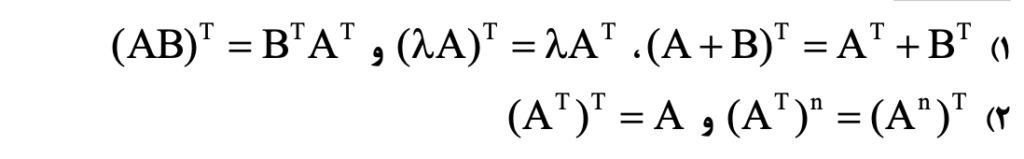
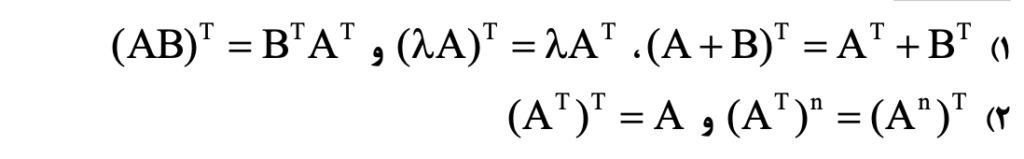
ویژگیهای ماتریس
ماتریسها هنگامی که عملیات ماتریسی رویشان اعمال می شود از چند ویژگی اساسی تبعیت می کنند. این ویژگی ها پایه و اساس جبر ماتریسی به حساب میآیند:
قانون شرکتپذیری
فرض کنید که A، B و C ماتریس هایی با ابعاد مساوی باشند. قانون شرکتپذیری برای عملیات جمع بهاین صورت است:
A+(B+C)=(A+B)+C
فرض کنید A یک ماتریس m×p و B ماتریسی p×q باشد و C ماتریسی q×n باشد. قانون شرکتپذیری برای ضرب اینگونه است:
A(BC)=(AB)C
قانون توزیعپذیری
فرض کنید که A یک ماتریس m×p باشد و B و C ماتریسهای p×n باشند. در این حالت قانون توزیعپذیری اینطور بیان میشود:
A(B+C)=AB+AC
همینطور اگر A یک ماتریس p×n باشد و B و C ماتریسهای m×p باشند، قانون توزیعپذیری بهاین صورت بیان میشود:
(B+C)A=BA+CA
برای آشنایی با طرز مطالعه ریاضی عمومی برای کنکور کارشناسی ارشد این مطلب را مطالعه کنید:
طرز اصولی مطالعه ریاضی عمومی ۱ و ۲ چگونه است؟
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

