موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد. ضریب این درس در کنکور رشته مدیریت کسب و کار ۲ است و اهمیت آن بر داوطلبان پوشیده نیست. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید. حد و محدودیت های آن از مباحث فصل دوم ریاضی عمومی است.
اهمیت درس ریاضی عمومی ۱ و ۲
ریاضی عمومی ۱ و ۲ از دروس پایهای رشتههای مختلف است. اهمیت این درس به سه دلیل عمده بازمیگردد؛ اولین دلیل این است که این درس جزو سرفصلهای امتحانی بسیار مهم رشتههای مختلف است. دلیل دوم به محتوای ارائهشده در این درس بازمیگردد. محتوای این درس بهقدری مهم است که آشنایی با مفاهیم آن به درک مفاهیم سایر درسهای دورهی کارشناسی و سایر مواد آزمون کارشناسیارشد کمک شایانی میکند. سومین دلیل اهمیت این درس و کلاس آنلاین ریاضی عمومی ۱ و ۲ نوع نگاهی است که در حل مسائل این درس وجود دارد؛ این نگاه عاملی اساسی در شکلگیری تفکر انتقادی در حل مسائل است.
طرز اصولی مطالعه ریاضی عمومی ۱ و ۲ چگونه است؟
در این سری از مقالات برخی از موضوعات مهم دروس را با نگاه آموزشی و به صورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید.
حد
حد در لغت به معنای مرز و محدودیت میباشد. در ریاضیات، حد (به انگلیسی: Limit)، مقداری است که یک تابع با نزدیک شدن ورودی به مقداری، به آن نزدیک میشود ولی هیچگاه به آن نمیرسد. حد، یک مفهوم اساسی در حسابان و در حالت کلی، در آنالیز ریاضی است و در تعریف پیوستگی، مشتق و انتگرال کاربرد دارد. حد، رفتار یک تابع را بیان میکند. در واقع، رفتار آن را در نقاط روی صفحه یا در بینهایت ارزیابی میکند.
محدودیتهای حدی
در توابع اگر محدودیتی در آنها وجود نداشته باشد عدد را به سادگی در تابع جایگذاری کرده و نیازی به محاسبه حد چپ و راست ندارین. در برخی دیگر از توابع به دلیل محدودیت های حدی نیاز به محاسبه جداگانه حد چپ و راست داریم.
توابع کسری
محدودیت در توابع کسری، در ریشه مخرج وجود دارد. هرگاه در توابع کسری حد به سمت ریشه مخرج برود نیاز است تا حد را شکسته و جداگانه محاسبه کنیم. تنها در صورتی که بتوانیم با روشهایی مانند همارزی یا هوپیتال، ریشه مخرج را از بین ببریم تابع در آن نقطه دارای حد خواهد بود.


توابع رادیکالی
در توابع رادیکالی در صورتیکه رادیکال فرجه فرد باشد محدودیت حدی نداریم. در صورتیکه رادیکال فرجه زوج باشد، ریشه عبارت زیر رادیکال محدودیت ماست. از آنجاییکه در توابع رادیکالی با فرجه زوج زیر رادیکال نمیتواند منفی شود به همین دلیل محدودیت حدی است.
توابع لگاریتمی
محدودیت در توابع لگاریتمی ریشه عبارت جلوی لگاریتم است. در این توابع چون می تواند یک شاخه وجود نداشته باشد تابع در ریشه عبارات وجود ندارد.
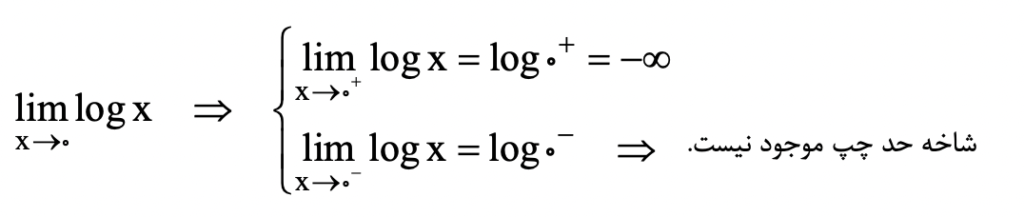
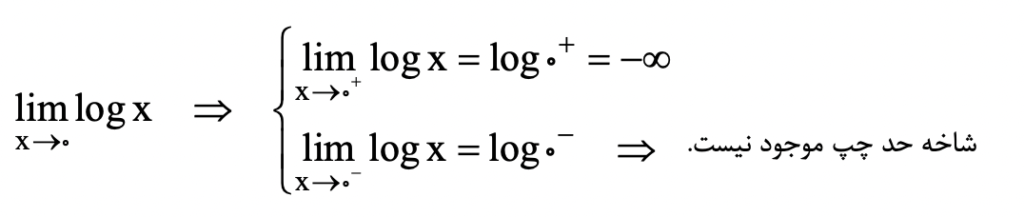
توابع قدر مطلق
در توابع قدرمطلقی، علامت تابع درون قدرمطلق قبل و بعد ریشه تابع متفاوت است. به همین دلیل در این توابع محدودیت وجود دارد. باید ابتدا حد چپ و راست را جدا کنیم تا علامت تابع مورد نظر را بدست آوریم. سپس باید حد چپ و راست را محاسبه کنیم و درصورتی که حد در چپ و راست برابر باشد تابع دارای حد است.
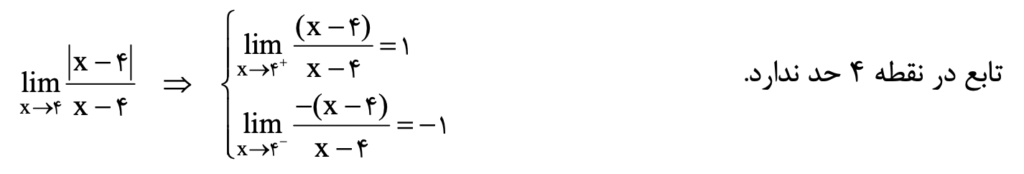
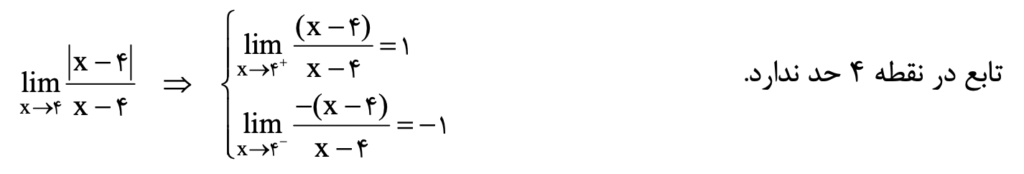
تابع براکتی
محدودیت توابع براکتی نیز مشابه قدرمطلق است. در این توابع تعیین مقدار میکنیم. در توابع براکتی عددی که داخل براکت را صحیح کند اهمیت دارد. در این نقاط باید حد چپ و راست تابع در نقاطی که تابع صحیح میشود محاسبه شود. در صورتی که حد چپ و راست برابر باشند تابع دارای حد است.
توابع چندضابطهای
در توابع چندضابطهای محدودیت میتواند در عدد مرزی ضابطهها وجود داشته باشد. در صورتی که مقدار تابع در مرز دو ضابطه برابر نباشد، تابع حد نخواهد داشت.
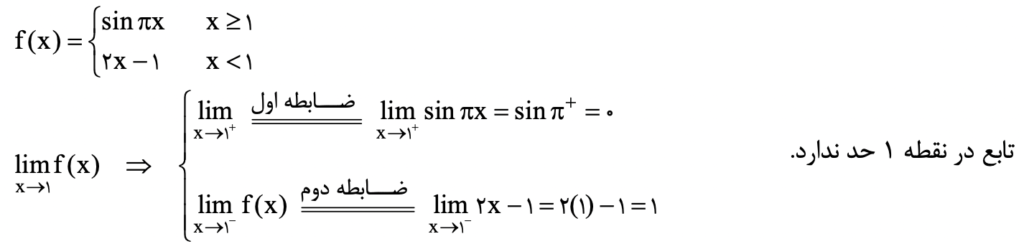
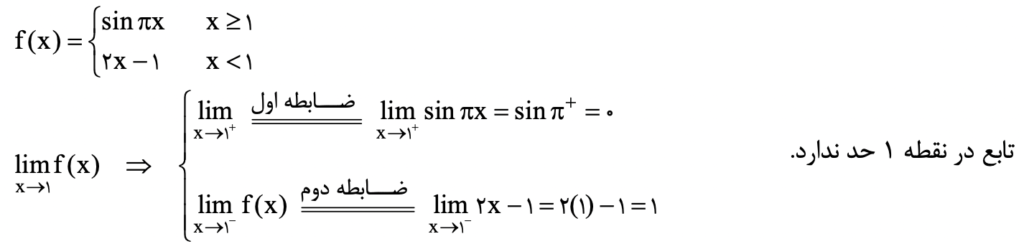
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

