نظریه گراف – پلی بین ریاضیات و دنیای واقعی

نظریه گراف (Graph Theory) یکی از شاخه‌های مهم و کاربردی در ریاضیات و علوم کامپیوتر است که به مطالعه گراف‌ها و خواص آن‌ها می‌پردازد. گراف‌ها ابزاری قدرتمند برای مدل‌سازی روابط و تعاملات پیچیده در دنیای واقعی هستند. با استفاده از گراف‌ها، می‌توان ساختارهای مختلفی را مدل‌سازی کرد، از شبکه‌های اجتماعی گرفته تا مسیرهای حمل و نقل و حتی ساختارهای مولکولی. در این مقاله، به بررسی نظریه گراف، تاریخچه، انواع، کاربردها، مفاهیم پایه‌ای و پیشرفته، الگوریتم‌ها و پژوهش‌های جدید در این زمینه خواهیم پرداخت. هدف این است که با فهم بهتر این نظریه، بتوانیم از آن در حل مسائل پیچیده استفاده کنیم.

تعریف نظریه گراف

نظریه گراف شاخه‌ای از ریاضیات است که به مطالعه گراف‌ها می‌پردازد. یک گراف شامل مجموعه‌ای از راس‌ها (یا گره‌ها) و یال‌ها (یا لبه‌ها) است که این راس‌ها را به هم متصل می‌کنند. راس‌ها نماینده اشیاء یا نقاطی هستند و یال‌ها روابط یا اتصالات بین این اشیا را نشان می‌دهند. این ساختار ساده اما قدرتمند می‌تواند برای مدل‌سازی بسیاری از سیستم‌های پیچیده مورد استفاده قرار گیرد. به عنوان مثال، یک شبکه اجتماعی می‌تواند به صورت یک گراف مدل‌سازی شود که در آن کاربران به عنوان راس‌ها و روابط دوستانه به عنوان یال‌ها نشان داده می‌شوند.

تاریخچه نظریه گراف

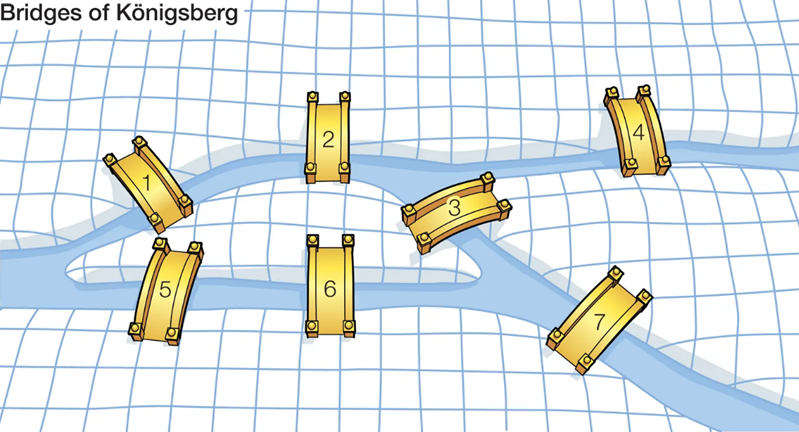
نظریه گراف در قرن هجدهم میلادی توسط لئونارد اویلر (Leonhard Euler) پایه‌گذاری شد. اویلر مسئله پل‌های کونیگسبرگ را که به مسئله گذر از همه پل‌ها بدون عبور دوباره از هیچ پلی مربوط بود، با استفاده از گراف‌ها حل کرد و اساس این نظریه را بنا نهاد. این مسئله به عنوان نخستین مسئله نظریه گراف شناخته می‌شود و الهام‌بخش بسیاری از پژوهش‌های بعدی در این زمینه بوده است.

مسئله پل‌های کونیگسبرگ

شهر کونیگسبرگ، که امروزه به‌نام کالینینگراد و در روسیه است، بر روی رودخانه پرگول قرار داشت و شامل چهار بخش اصلی بود که توسط هفت پل به یکدیگر متصل می‌شدند. سؤال اصلی این بود که آیا می‌توان مسیری پیدا کرد که هر پل را دقیقاً یک بار عبور کرده و به نقطه شروع بازگشت. اویلر با استفاده از یک مدل گراف، این مسئله را حل کرد و نشان داد که چنین مسیری وجود ندارد. او با معرفی مفاهیم راس‌ها و یال‌ها، پایه‌گذار نظریه گراف شد.

تحولات قرن نوزدهم

پس از اویلر، نظریه گراف به طور گسترده‌ای مورد توجه ریاضی‌دانان قرار گرفت. در قرن نوزدهم، ریاضی‌دانانی چون آرتور کیلی و جیمز جوزف سیلوستر به توسعه این نظریه پرداختند. کیلی نیز در سال ۱۸۵۷ مطالعاتی در زمینه درخت‌ها (گراف‌های بدون حلقه) انجام داد و مفاهیم اساسی مرتبط با درخت‌ها را معرفی کرد. گوستاو کیرشهف، فیزیک‌دان آلمانی نیز در سال ۱۸۴۵ قوانین مدارهای الکتریکی خود را با استفاده از گراف‌ها فرموله کرد که به تحلیل شبکه‌های الکتریکی کمک کرد.

آغاز قرن بیستم و توسعه‌های مدرن

در آغاز قرن بیستم، نظریه گراف به طور فزاینده‌ای مورد توجه قرار گرفت و کاربردهای جدیدی پیدا کرد. ریاضی‌دانانی مانند کامیل جوردن (Camille Jordan) و ویلیام توماس تات (William Thomas Tutte) در توسعه مفاهیم جدید و کاربردهای نظریه گراف نقش داشتند. جوردن در سال ۱۸۶۹ قضیه جوردن (Jordan curve theorem) را معرفی کرد که به ساختار گراف‌ها مرتبط است. تات نیز با کارهای خود در زمینه گراف‌های مسطح و چندجمله‌ای‌های گراف‌ها، به توسعه این نظریه کمک کرد.

در نیمه دوم قرن بیستم، نظریه گراف به یکی از ابزارهای اصلی در علوم کامپیوتر تبدیل شد. الگوریتم‌های گراف مانند الگوریتم دایجسترا (۱۹۵۹) برای یافتن کوتاه‌ترین مسیرها و الگوریتم پریم (۱۹۵۷) برای یافتن درخت پوشای کمینه، به طور گسترده‌ای در مسیریابی و بهینه‌سازی شبکه‌ها مورد استفاده قرار گرفتند.

مفاهیم پایه‌ای در نظریه گراف

نظریه گراف شامل چندین مفهوم پایه‌ای است که برای فهم بهتر گراف‌ها و تحلیل آن‌ها ضروری هستند.

راس

راس‌ها (Vertex) یا گره‌ها (Nodes) اجزای اصلی یک گراف هستند که می‌توانند نماینده اشیا یا افراد باشند. هر راس می‌تواند با یک یا چند راس دیگر از طریق یال‌ها در ارتباط باشد. دو راسی که به‌واسطه حداقل یک یال به‌یکدیگر متصل شده باشند را دو راس مجاور می‌گویند. مجموعه رئوس یک گراف را عموما با V نشان می‌دهند. در یک شبکه اجتماعی، راس‌ها می‌توانند نماینده افراد و در یک شبکه کامپیوتری، نماینده سرورها یا دستگاه‌ها باشند.

یال

یال‌ها یا لبه‌ها (Edges) ارتباطات بین راس‌ها را نشان می‌دهند و می‌توانند جهت‌دار یا بدون جهت باشند. یال‌ها می‌توانند نمایانگر روابط، جریان‌ها یا اتصالات بین عناصر مختلف باشند. مجموعه یال‌های یک گراف را عموما با E نشان می‌دهند. در یک شبکه جاده‌ای، یال‌ها می‌توانند نشان‌دهنده جاده‌ها باشند و در یک شبکه ارتباطی، نشان‌دهنده لینک‌های ارتباطی بین دستگاه‌ها.

درجه راس

درجه (Degree) راس تعداد یال‌هایی است که به یک راس متصل می‌شوند. این مفهوم می‌تواند اطلاعاتی درباره مرکزیت و اهمیت یک راس در گراف ارائه دهد. به عنوان مثال، در یک شبکه اجتماعی، درجه یک راس می‌تواند نشان‌دهنده تعداد دوستان یا ارتباطات یک فرد باشد و در یک شبکه ارتباطی، نشان‌دهنده تعداد لینک‌های یک دستگاه باشد.

گذر

گذر (Trail) یک دنباله‌ای از رئوس و یال‌ها است که در آن هیچ یالی تکراری وجود ندارد. به عبارتی دیگر، در گذر هر یال حداکثر یک بار ظاهر می‌شود اما ممکن است رئوس تکرار شوند.

مدار

مدار (Circuit) یک نوع خاص از گذر است که شروع و پایان آن در یک راس مشترک است. به عبارتی دیگر، مدار یک گذر بسته است که در آن هیچ یالی تکراری وجود ندارد و آغاز و پایان در یک راس قرار دارند.

مسیر

مسیر (Path) یک دنباله‌ای از رئوس و یال‌ها است که در آن هیچ یالی و هیچ راس تکراری‌ای وجود ندارد. یعنی در مسیر، هر راس و هر یال حداکثر یک بار ظاهر می‌شوند.

دور

دور (Cycle) یک نوع خاص از مسیر است که شروع و پایان آن در یک راس مشترک است. به عبارتی دیگر، دور یک مسیر بسته است که در آن هیچ یال و هیچ راس تکراری‌ای وجود ندارد به جز راس شروع و پایان که مشترک هستند.

مکمل گراف

مکمل گراف (Complement Graph) یک گراف G که به صورت G=(V,E)  تعریف می‌شود، گرافی است که مجموعه راس‌های آن با مجموعه راس‌های گراف اصلی G برابر است، اما مجموعه یال‌های آن شامل تمام یال‌هایی است که در G وجود ندارند. به عبارت دیگر، اگر ‘G مکمل گراف G باشد، بین هر دو راس U و V یک یال در ‘G وجود دارد اگر و تنها اگر این یال در G وجود نداشته باشد.

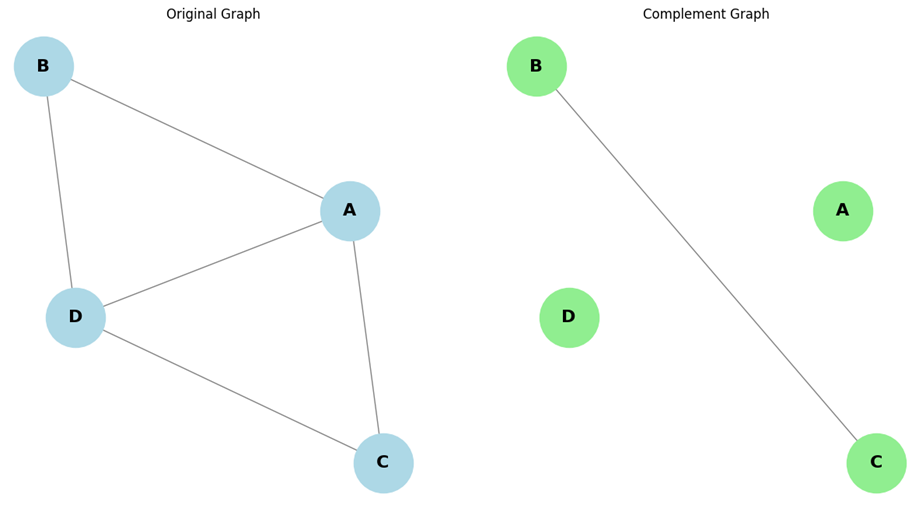
ویژگی‌های مکمل یک گراف

• مجموعه راس‌ها: مجموعه راس‌های گراف مکمل با گراف اصلی یکسان است.
• مجموعه یال‌ها: مجموعه یال‌های گراف مکمل شامل تمام یال‌های ممکن است که در گراف اصلی وجود ندارند.
• تعداد یال‌ها: اگر گراف اصلی G دارای n راس و e یال باشد، مکمل آن دارای n(n-1)/2 - e یال خواهد بود

گراف هم‌ریخت

دو گراف G₁ و G₂ هم‌ریخت (Isomorphic Graph) هستند اگر بین مجموعه راس‌های آن‌ها یک نگاشت یک‌به‌یک وجود داشته باشد به طوری که هر یال بین دو راس در G₁​ با یال بین تصاویر آن‌ها در G₂ ​مطابقت داشته باشد. به عبارت دیگر، گراف‌های هم‌ریخت ساختارهای مشابه دارند، حتی اگر ظاهر آن‌ها متفاوت باشند.

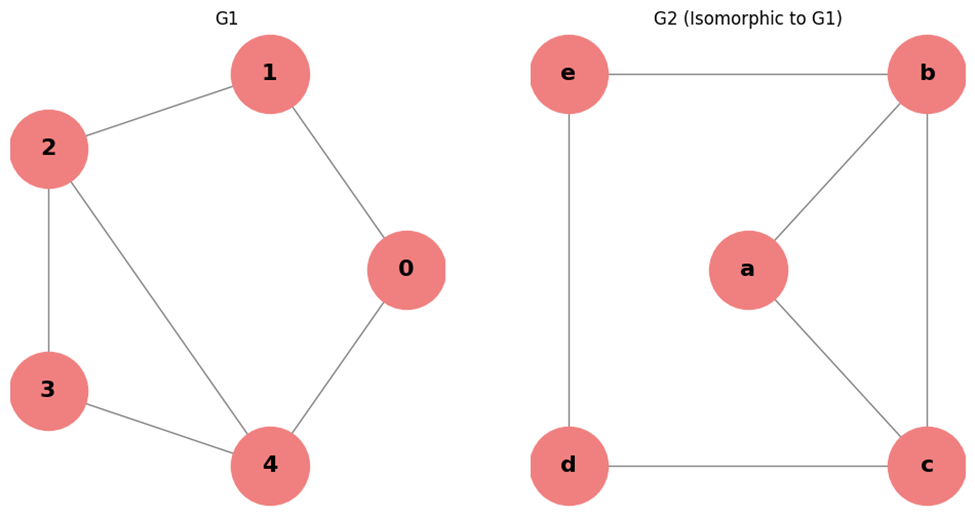
در این دو گراف اگر نگاشت:

\large 0 \rightarrow d
\large 1 \rightarrow e
\large 2 \rightarrow b
\large 3 \rightarrow a
\large 4 \rightarrow c

را در نظر بگیریم، می‌بینیم که گراف G₂ هم‌ریخت گراف G₁ است. برای بررسی این موضوع نیز می‌توانیم درجه رئوس همتا را بررسی کنیم. مثلا گره‌های ۲ و ۴ در گراف G₁ درجه ۳ هستند و گره‌های b و c نیز در گراف G₂ درجه ۳ هستند. یا اینکه بین گره‌های ۰ و ۱ در گراف نخست یک یال قرار دارد و بین گره‌های d و e در گراف دوم نیز دقیقا یک یال قرار دارد. با ادامه این بررسی‌ها می‌توان هم‌ریختی این دو گراف را اثبات کرد.

ویژگی‌های گراف‌های هم‌ریخت

• نگاشت یک‌به‌یک: بین راس‌های دو گراف هم‌ریخت یک نگاشت یک‌به‌یک وجود دارد که یال‌ها را حفظ می‌کند.
• حفظ ساختار: گراف‌های هم‌ریخت ساختارهای مشابه دارند و به همین دلیل از نظر توپولوژیکی یکسان هستند.
• درجه راس‌ها: در گراف‌های هم‌ریخت، درجات راس‌های متناظر برابر است.

گراف‌ها ساختارهای بنیادین متنوعی دارند که هر کدام ویژگی‌ها و کاربردهای خاص خود را دارند. در این بخش، به بررسی انواع مختلف گراف‌ها و ویژگی‌های هر کدام می‌پردازیم.

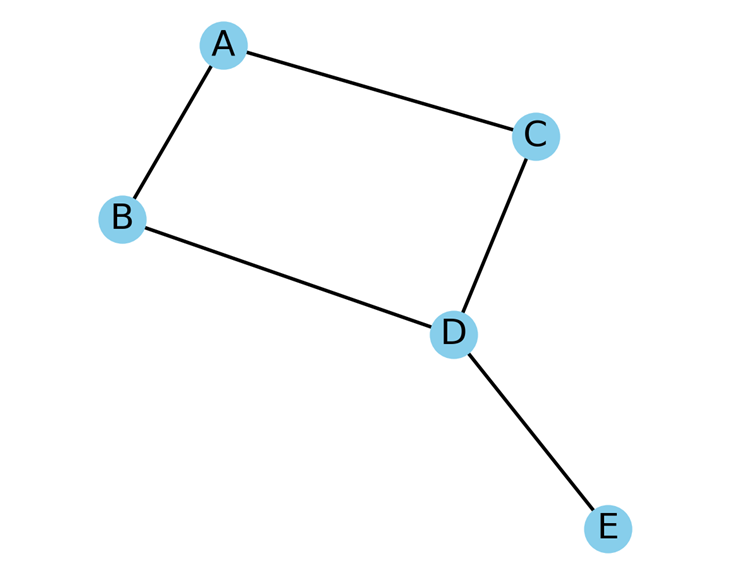
گراف ساده

گراف ساده یک نوع گراف است که در آن هر یال دو راس را به هم متصل می‌کند و هیچ یال تکراری یا طوقه‌ای (یالی که از یک راس به همان راس می‌رود) وجود ندارد. در گراف ساده، هر دو راس می‌توانند حداکثر با یک یال به هم متصل باشند و هیچ راسی به خودش متصل نیست. این نوع گراف‌ها ساده‌ترین شکل گراف‌ها هستند و معمولاً برای مدل‌سازی ساختارهای پایه‌ای و ابتدایی استفاده می‌شوند. به عنوان مثال، یک گراف ساده می‌تواند یک شبکه اجتماعی ابتدایی را نشان دهد که در آن هر فرد تنها یک رابطه مستقیم با هر فرد دیگر دارد.

گراف جهت‌دار

گراف جهت‌دار یا دیگراف (Directed Graph) نوعی گراف است که در آن یال‌ها دارای جهت هستند. به عبارت دیگر، هر یال در یک گراف جهت‌دار از یک راس شروع شده و به یک راس دیگر ختم می‌شود. این جهت‌دار بودن نشان می‌دهد که ارتباط یا جریان تنها در یک جهت خاص برقرار است.

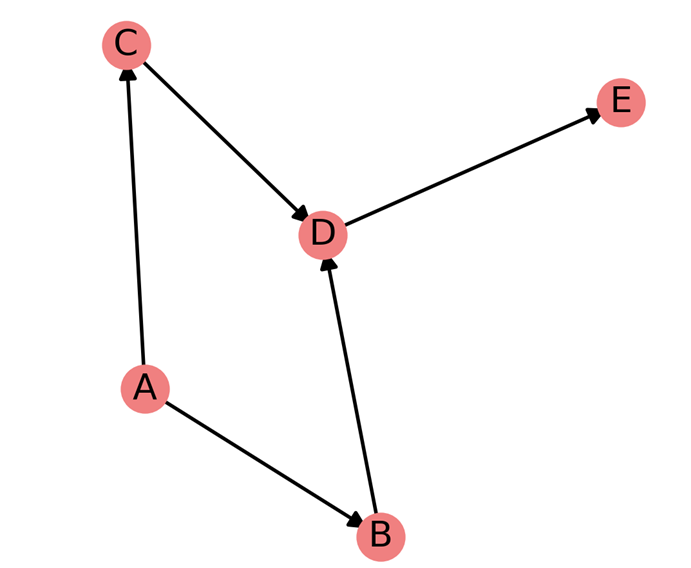
ویژگی‌های گراف جهت‌دار

گراف جهت‌دار ویژگی‌هایی دارد که در زیر به آن‌ها اشاره می‌کنیم:

جهت یال‌ها

در گراف‌های جهت‌دار، هر یال به صورت یک جفت مرتب (u, v) نمایش داده می‌شود که نشان‌دهنده یالی است که از راس u به راس v می‌رود.

درجه ورودی و خروجی

در یک گراف جهت‌دار، هر راس دارای درجه ورودی (in-degree) و درجه خروجی (out-degree) است. درجه ورودی تعداد یال‌هایی است که به یک راس وارد می‌شوند و درجه خروجی تعداد یال‌هایی است که از آن راس خارج می‌شوند.

مسیر جهت‌دار

مسیری که در آن جهت یال‌ها رعایت شود، به‌عنوان مسیر جهت‌دار شناخته می‌شود. به‌عنوان مثال، اگر یال (u, v) و یال (v, w) در یک گراف وجود داشته باشند، مسیر جهت‌دار u → v → w برقرار است.

حلقه‌ها

در گراف‌های جهت‌دار، حلقه‌ها (Cycles) نیز جهت‌دار هستند. یک حلقه جهت‌دار مسیری است که از یک راس شروع شده و پس از عبور از چند راس دیگر به همان راس بازمی‌گردد.

کاربردهایی از گراف جهت‌دار

گراف‌های جهت‌دار در بسیاری از کاربردهای واقعی مورد استفاده قرار می‌گیرند. برخی از مثال‌های آن عبارتند از:

شبکه‌های جاده‌ای

در شبکه‌های جاده‌ای، برخی جاده‌ها ممکن است یک‌طرفه باشند. گراف جهت‌دار می‌تواند این شبکه‌ها را به خوبی مدل‌سازی کند. این امر به یافتن کوتاه‌ترین مسیرها و جلوگیری از اشتباهات مسیریابی در جاده‌های یک‌طرفه کمک می‌کند. همچنین در سیستم‌های ناوبری و GPS، گراف‌های جهت‌دار برای مدل‌سازی دقیق جاده‌های یک‌طرفه و ارائه مسیرهای بهینه به کاربران استفاده می‌شوند.

شبکه‌های اجتماعی

در بسیاری از شبکه‌های اجتماعی، روابط بین کاربران جهت‌دار هستند. به عنوان مثال، در توییتر، یک کاربر می‌تواند کاربر دیگری را دنبال کند بدون اینکه لزوماً توسط آن کاربر دنبال شود. این روابط یک‌طرفه با استفاده از گراف‌های جهت‌دار مدل‌سازی می‌شوند. گراف‌های جهت‌دار به تحلیل دقیق‌تر و جامع‌تر این روابط کمک می‌کنند. از سویی دیگر، بسیاری از روابط در شبکه‌های اجتماعی به صورت یک‌طرفه هستند، مانند لایک‌ کردن‌ها، اشتراک‌گذاری‌ها و دنبال کردن‌ها. گراف‌های جهت‌دار به مدل‌سازی این روابط و بررسی الگوهای تعامل کاربران کمک می‌کنند. با استفاده از این گراف‌ها، می‌توان تأثیرات مختلف کاربران بر رفتار یکدیگر را تحلیل و بررسی کرد. این تحلیل‌ها به شناسایی افراد تأثیرگذار و بررسی دینامیک‌های اجتماعی کمک می‌کنند.

گراف وزن‌دار

گراف وزن‌دار نوعی گراف است که در آن هر یال دارای یک وزن (یا هزینه) مشخص است. این وزن می‌تواند نشان‌دهنده مقادیر مختلفی مانند فاصله، هزینه، زمان یا هر معیار دیگری باشد که به روابط بین راس‌ها مرتبط است. گراف وزن‌دار می‌تواند جهت‌دار یا بدون جهت باشد.

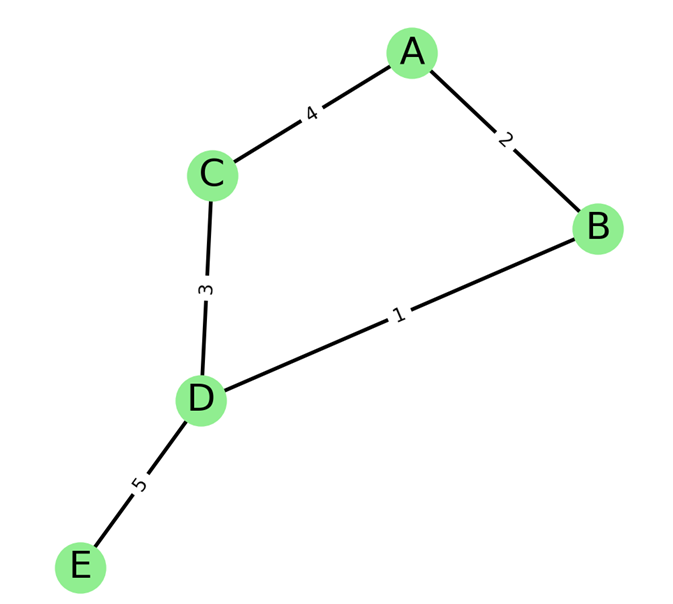
ویژگی‌های گراف وزن‌دار

گراف وزن‌دار ویژگی‌هایی دارد که در زیر به آن‌ها اشاره می‌کنیم:

وزن یال‌ها

هر یال در گراف وزن‌دار دارای یک وزن مشخص است که به صورت یک عدد نشان داده می‌شود. این وزن‌ها می‌توانند مقادیر مثبت، منفی یا صفر باشند، هرچند در بسیاری از کاربردهای واقعی وزن‌ها معمولاً مثبت هستند.

ماتریس مجاورت وزن‌دار

برای نمایش گراف وزن‌دار، می‌توان از ماتریس مجاورت وزن‌دار استفاده کرد. در این ماتریس، هر ورودی نشان‌دهنده وزن یال بین دو راس است. اگر بین دو راس یالی وجود نداشته باشد، مقدار ورودی صفر یا بی‌نهایت خواهد بود.

مسیر وزن‌دار

در یک گراف وزن‌دار، مجموع وزن‌های یال‌های موجود در یک مسیر، وزن کلی آن مسیر را تعیین می‌کند. این مفهوم در مسائل مسیریابی و بهینه‌سازی بسیار مهم است.

کاربردهایی از گراف وزن‌دار

گراف‌های وزن‌دار در بسیاری از کاربردهای واقعی مورد استفاده قرار می‌گیرند. برخی از مثال‌ها عبارتند از:

شبکه‌های حمل و نقل

در شبکه‌های جاده‌ای و حمل و نقل، وزن یال‌ها می‌تواند نشان‌دهنده معیارهای مختلفی باشد که برای بهینه‌سازی و مسیریابی استفاده می‌شوند. برخی از این معیارها را در زیر بررسی می‌کنیم:

• فاصله: وزن یال‌ها می‌تواند نشان‌دهنده فاصله بین دو نقطه باشد. استفاده از این اطلاعات می‌تواند به یافتن کوتاه‌ترین مسیر بین دو نقطه کمک کند.
• زمان سفر: وزن یال‌ها می‌تواند نشان‌دهنده زمان مورد نیاز برای سفر بین دو نقطه باشد. این اطلاعات برای بهینه‌سازی زمان سفر و یافتن سریع‌ترین مسیر استفاده می‌شوند.
• هزینه سوخت: وزن یال‌ها می‌تواند نشان‌دهنده هزینه سوخت برای سفر بین دو نقطه باشد. استفاده از این اطلاعات می‌تواند به کاهش هزینه‌های سفر و بهینه‌سازی مصرف سوخت کمک کند.

شبکه‌های ارتباطی

در شبکه‌های کامپیوتری و مخابراتی، وزن یال‌ها می‌تواند نشان‌دهنده معیارهای مختلفی باشد که برای بهینه‌سازی انتقال داده‌ها و ارتباطات استفاده می‌شوند. برخی از این معیارها عبارتند از:

• پهنای باند: وزن یال‌ها می‌تواند نشان‌دهنده پهنای باند موجود برای انتقال داده‌ها بین دو نقطه باشد. این اطلاعات برای بهینه‌سازی استفاده از پهنای باند و جلوگیری از ازدحام شبکه مفید هستند.
• تأخیر: وزن یال‌ها می‌تواند نشان‌دهنده تأخیر زمانی در انتقال داده‌ها بین دو نقطه باشد. استفاده از این اطلاعات می‌تواند به کاهش تأخیر و بهبود کیفیت خدمات ارتباطی کمک کند.
• هزینه انتقال: وزن یال‌ها میک‌تواند نشان‌دهنده هزینه انتقال داده‌ها بین دو نقطه باشد. استفاده از این اطلاعات می‌تواند به کاهش هزینه‌های انتقال داده‌ها و بهینه‌سازی هزینه‌ها کمک کند.

مدل‌سازی اقتصادی

در مدل‌های اقتصادی، وزن یال‌ها می‌تواند نشان‌دهنده هزینه‌ها یا سودهای مربوط به روابط اقتصادی بین عوامل مختلف باشد. برخی از این کاربردها عبارتند از:

• روابط تجاری بین کشورها: وزن یال‌ها می‌تواند نشان‌دهنده حجم تجارت و تبادلات اقتصادی بین کشورها باشد. استفاده از این اطلاعات می‌تواند به تحلیل و بهبود روابط تجاری بین‌المللی کمک کند.
• سودها و درآمدها: وزن یال‌ها می‌تواند نشان‌دهنده سودها و درآمدهای حاصل از روابط اقتصادی بین عوامل مختلف باشد. این اطلاعات می‌تواند به تحلیل و پیش‌بینی سودآوری و بازدهی سرمایه‌گذاری‌ها کمک کند.
• هزینه‌های تولید و توزیع: وزن یال‌ها می‌تواند نشان‌دهنده هزینه‌های تولید و توزیع کالاها و خدمات بین عوامل اقتصادی باشد. استفاده از این اطلاعات می‌تواند به بهینه‌سازی هزینه‌های تولید و توزیع کمک کند.

گراف چندگانه

گراف چندگانه یا مولتی‌گراف (Multigraph) نوعی گراف است که در آن می‌تواند بیش از یک یال بین هر جفت راس وجود داشته باشد. به عبارت دیگر، در یک گراف چندگانه، بین دو راس می‌توان چندین یال موازی وجود داشته باشد که هر کدام نمایانگر یک نوع رابطه یا مسیر مختلف بین آن دو راس هستند.

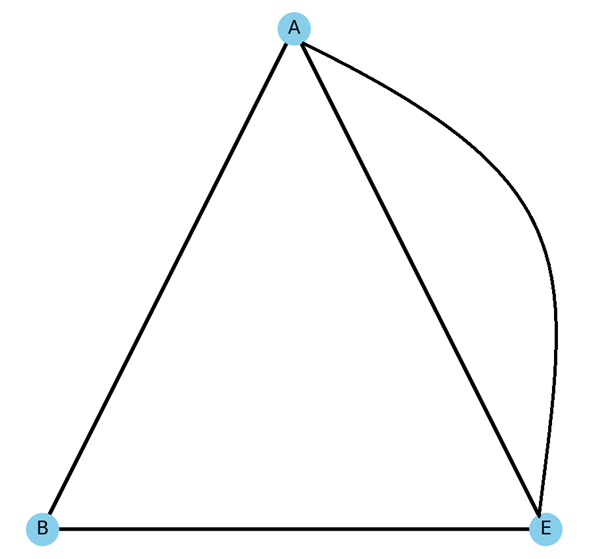
ویژگی‌های گراف چندگانه

گراف چندگانه ویژگی‌هایی دارد که در زیر به آن‌ها اشاره می‌کنیم:

یال‌های موازی

اصلی‌ترین ویژگی گراف چندگانه این است که بین هر جفت راس ممکن است بیش از یک یال وجود داشته باشد. این یال‌ها به عنوان یال‌های موازی شناخته می‌شوند.

یال‌های جهت‌دار و بدون جهت

گراف چندگانه می‌تواند شامل یال‌های جهت‌دار و بدون جهت باشد. در گراف‌های جهت‌دار چندگانه، یال‌های موازی می‌توانند جهت‌های مختلفی داشته باشند.

کاربردهایی از گراف چندگانه

گراف‌های چندگانه در بسیاری از کاربردهای واقعی مورد استفاده قرار می‌گیرند. برخی از این مثال‌ها عبارتند از:

مدل‌سازی روابط اجتماعی

در مدل‌سازی روابط اجتماعی، ممکن است چندین نوع رابطه بین دو فرد وجود داشته باشد، مانند روابط خانوادگی، دوستانه و کاری. هر نوع رابطه می‌تواند یک یال در گراف چندگانه باشد. مثلا دو نفر می‌توانند در عین اینکه دوست یکدیگر هستند، همکار نیز باشند. این ویژگی به تحلیل دقیق‌تر و جامع‌تر روابط اجتماعی کمک می‌کند.

شبکه‌های حمل و نقل

در شبکه‌های حمل و نقل، ممکن است چندین مسیر مختلف بین دو شهر وجود داشته باشد. هر مسیر می‌تواند یک یال در گراف چندگانه را نشان دهد. این ویژگی به مدل‌سازی و تحلیل دقیق‌تر شبکه‌های حمل و نقل کمک می‌کند.

شبکه‌های کامپیوتری

در شبکه‌های کامپیوتری، ممکن است بین دو دستگاه چندین لینک فیزیکی مانند کابل‌های اترنت یا فیبر نوری وجود داشته باشد که هر کدام نمایانگر یک یال در گراف چندگانه هستند. در شبکه‌های مخابراتی، ممکن است بین دو دستگاه چندین لینک منطقی مانند تونل‌های VPN یا ارتباطات بی‌سیم وجود داشته باشد که هر کدام نمایانگر یک یال در گراف چندگانه هستند.

گراف کامل

گراف کامل (Complete Graph) نوعی گراف است که در آن هر جفت راس توسط یک یال به هم متصل شده‌اند. یعنی در یک گراف کامل با n راس، هر راس به n-1 راس دیگر متصل است. گراف کامل به صورت K_n نشان داده می‌شود.

ویژگی‌های گراف کامل

گراف کامل ویژگی‌هایی دارد که در زیر به آن‌ها اشاره می‌کنیم:

تعداد یال‌ها

یک گراف کامل بدون جهت با n راس، n(n−1)/2  یال دارد. این فرمول به این دلیل است که هر راس با n−1 راس دیگر در ارتباط است، اما به دلیل عدم تکرار یال‌ها (یال‌ها دو بار شمرده نمی‌شوند)، تقسیم بر ۲ می‌شود. در گراف کامل جهت‌دار چون می‌توان بین هر دو راس دو یال رسم کرد (یکی از راس اول به سمت راس دوم و دیگری از راس دوم به سمت راس اول) تعداد یال‌ها برابر n(n-1) خواهد بود.

همبندی بالا

گراف‌های کامل دارای بالاترین میزان همبندی ممکن هستند، به این معنا که تعداد زیادی یال برای اتصال راس‌ها وجود دارد. این ویژگی باعث می‌شود که گراف کامل بسیار پایدار و مقاوم در برابر خرابی باشد؛ زیرا حتی با حذف برخی یال‌ها یا رئوس، ارتباطات بین رئوس باقی می‌ماند.

متقارن بودن

گراف‌های کامل به صورت متقارن هستند، به این معنا که ساختار گراف از هر نقطه مشاهده یکسان است. به عبارت دیگر، هیچ راسی نسبت به سایر رئوس برتری یا تفاوتی ندارد و تمامی رئوس نقش یکسانی در ساختار گراف ایفا می‌کنند. این ویژگی باعث می‌شود که تحلیل و بررسی گراف‌های کامل ساده‌تر باشد.

مثال‌هایی از گراف کامل بدون جهت

گراف کامل K₃: این گراف یک مثلث است که در آن سه راس وجود دارد و هر راس به دو راس دیگر متصل است. بنابراین ۳ یال دارد.

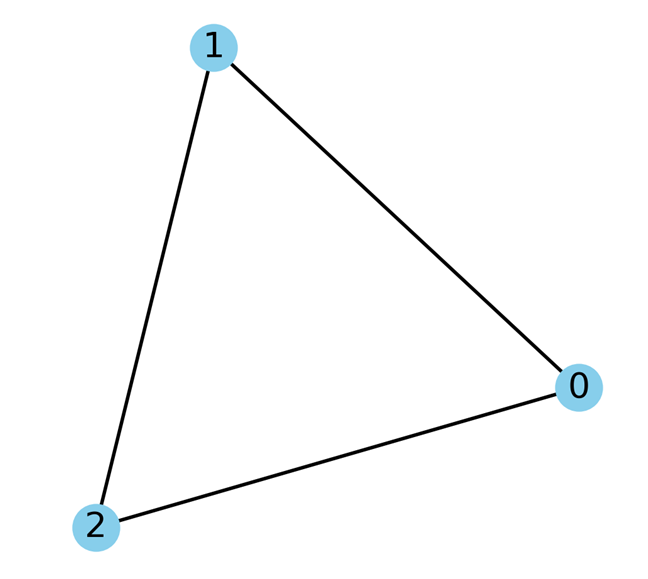
گراف کامل K₄: این گراف یک چهارضلعی است که در آن چهار راس وجود دارد و هر راس به سه راس دیگر متصل است. بنابراین ۶ یال دارد.

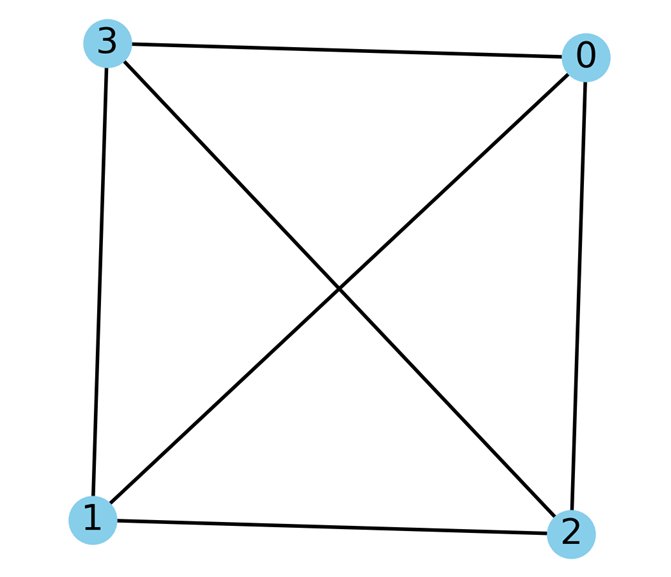
کاربردهای گراف کامل

گراف‌های کامل در بسیاری از کاربردهای واقعی مورد استفاده قرار می‌گیرند. برخی از این مثال‌ها عبارتند از:

مسائل بهینه‌سازی و تحقیق در عملیات

گراف‌های کامل در مسائل بهینه‌سازی و تحقیق در عملیات کاربرد فراوانی دارند. یکی از معروف‌ترین این مسائل، مسئله فروشنده دوره‌گرد (Travelling salesman problem) است. در این مسئله، یک فروشنده باید به چندین شهر سفر کند و به نقطه شروع بازگردد به گونه‌ای که مجموع مسافت طی شده حداقل باشد. از آنجایی که فروشنده باید تمامی مسیرهای ممکن بین شهرها را بررسی کند، گراف کامل بهترین مدل برای این مسئله است.

طراحی و تحلیل مدارهای الکترونیکی

در طراحی و تحلیل مدارهای الکترونیکی، گراف‌های کامل برای نمایش اتصالات بین نقاط مختلف مدار استفاده می‌شوند. در برخی از این مدارها، هر نقطه باید به تمامی نقاط دیگر متصل باشد تا در صورت ایجاد قطعی یا اختلال در یکی از مسیرها، ارتباط قطع نشود. در این حالت، گراف کامل بهترین مدل برای نمایش این اتصالات است.

گراف دو بخشی

گراف دو بخشی (Bipartite Graph) گرافی است که راس‌های آن را می‌توان به دو مجموعه مجزا تقسیم کرد به طوری که هیچ یالی بین راس‌های یک مجموعه وجود نداشته باشد. در گراف‌های دو بخشی، یال‌ها فقط بین رئوس دو بخش مختلف قرار دارند و هیچ یالی داخل یک بخش خاص نیست.

گراف‌ دو بخشی کامل

یک گراف دو بخشی کامل گرافی است که در آن هر راس از مجموعه اول به تمامی راس‌های مجموعه دوم متصل است. این نوع گراف‌ها به صورت K_m,n​ نشان داده می‌شوند که m تعداد راس‌های مجموعه اول و n تعداد راس‌های مجموعه دوم است. در این صورت، گراف m + n راس و m×n یال خواهد داشت.

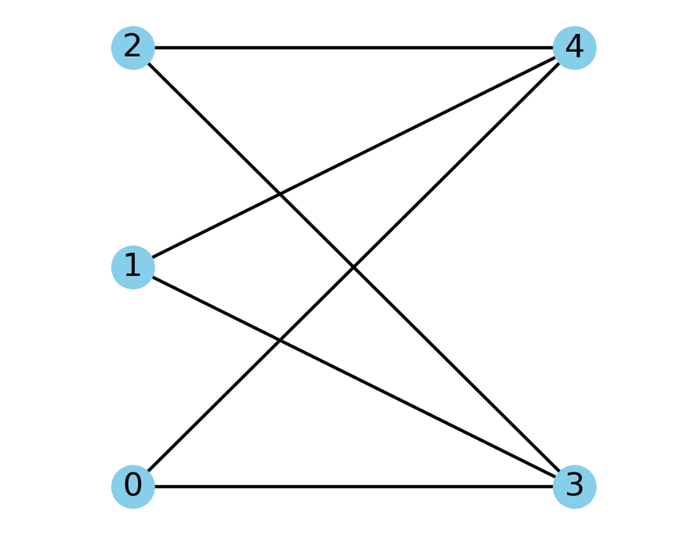
ویژگی‌های گراف دو بخشی

گراف دو بخشی ویژگی‌هایی دارد که در زیر به آن‌ها اشاره می‌کنیم:

نحوه شناسایی گراف دو بخشی

یک گراف تنها در صورتی دو بخشی است که بتوان رئوس آن را به دو مجموعه مجزا تقسیم کرد به گونه‌ای که هیچ یالی داخل یک مجموعه نباشد. یک راه دیگر برای شناسایی گراف دو بخشی، بررسی وجود دورهای (چرخه‌های) فرد طول است؛ اگر هیچ دور فرد طول در گراف وجود نداشته باشد، گراف دو بخشی است.

راه دیگری که برای تشخیص گراف‌های دو بخشی وجود دارد. به این صورت که اگر بتوان رئوس گراف را با دو رنگ طوری رنگ‌آمیزی کرد که هیچ دو راس مجاوری هم‌رنگ نباشند، آن گراف دو بخشی است.

حداکثر تعداد یال‌ها

تعداد یال‌های یک گراف دو بخشی محدود به تعداد رئوس در دو بخش مختلف است. اگر تعداد رئوس مجموعه اول برابر m و تعداد رئوس مجموعه دوم برابر n باشد، حداکثر تعداد یال‌های گراف دو بخشی برابر n×m خواهد بود. این تعداد یال در حالتی تشکیل خواهد شد که گراف، دو بخشی کامل باشد. تعداد یال‌های هر گراف دو بخشی دیگر کمتر از این عدد خواهد بود.

کاربردهای گراف دو بخشی

گراف‌های دو بخشی در بسیاری از کاربردهای واقعی مورد استفاده قرار می‌گیرند. برخی از مثال‌ها عبارتند از:

• مدل‌سازی سیستم‌های تطابق: مانند تطابق کارگران با مشاغل، دانشجویان با دانشگاه‌ها، بیماران با اهداکنندگان عضو و غیره.
• شبکه‌های کامپیوتری و ارتباطات: مدل‌سازی شبکه‌هایی که در آن‌ها دستگاه‌ها به سرورها یا روترها متصل می‌شوند.
• تحلیل داده‌های اجتماعی: مدل‌سازی ارتباطات بین گروه‌های مختلف مانند کاربران و محصولات، افراد و سازمان‌ها.
• تخصیص وظایف: در تخصیص وظایف به کارکنان، می‌توان از گراف دو بخشی استفاده کرد تا اطمینان حاصل شود که هیچ کارمندی بیش از حد مشغول نمی‌شود.

گراف اویلری

گراف اویلری یک نوع گراف است که در آن یک مدار اویلری وجود دارد، یعنی گذری که هر یال را دقیقاً یک بار ملاقات کند و به راس ابتدایی برگردد. اگر چنین گذری در گراف وجود داشته باشد، گراف اویلری نامیده می‌شود.

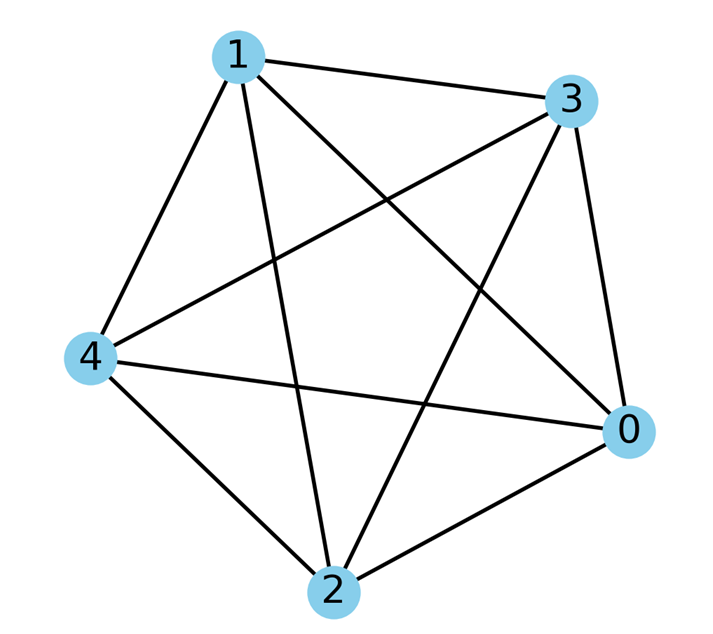
ویژگی‌های گراف اویلری

گراف اویلری ویژگی‌هایی دارد که در زیر به آن‌ها اشاره می‌کنیم:

گذر اویلری

گذر اویلری (Eulerian Trail) گذری در گراف است که هر یال را دقیقاً یک بار بازدید می‌کند، اما نیازی به بازگشت به راس ابتدایی نیست. به عبارت دیگر، گذر اویلری از یک راس شروع شده، به تمام یال‌ها می‌رود و در یک راس متفاوت پایان می‌یابد.

مدار اویلری

مدار اویلری (Eulerian Circuit) نوع خاصی از گذر اویلری است که در آن گذر به راس ابتدایی بازمی‌گردد. این بدین معناست که یک گذر اویلری از یک راس شروع کرده، هر یال را دقیقاً یک بار بازدید کرده و در پایان به همان راس شروع برمی‌گردد. وجود یک مدار اویلری در گراف، آن را به یک گراف اویلری تبدیل می‌کند.

شناسایی گراف اویلری

برای تشخیص اویلری بودن گراف باید دو شرط زیر هم‌زمان برقرار باشند:

• گراف باید متصل (همبند) باشد: به این معنی که بین هر دو راس یک مسیر وجود داشته باشد.
• در گراف‌های بدون جهت، همه رئوس باید دارای درجه زوج باشند: در این صورت، یک مدار اویلری وجود خواهد داشت که از هر راس شروع شده و به همان راس بازمی‌گردد.
• در گراف‌های جهت‌دار، درجه ورودی هر راسی باید با درجه خروجی‌‌اش برابر باشد، به‌جز احتمالا دو راس که در یکی از آن‌ها درجه ورودی‌ یک واحد بیشتر از درجه خروجی‌اش است و در دیگری درجه خروجی یک واحد بیشتر از درجه ورودی‌اش است.

کاربردهای گراف اویلری

گراف‌های اویلری در مسائل مختلفی از جمله موارد زیر کاربرد دارند:

طراحی مسیرهای خدماتی

یکی از کاربردهای اصلی گراف‌های اویلری در طراحی مسیرهای خدماتی مانند جمع‌آوری زباله، پست، خدمات تحویل کالا و غیره است. این مسائل شامل یافتن مسیرهایی هستند که از تمامی خیابان‌ها (یال‌ها) یک بار عبور کنند و در صورت امکان به نقطه شروع بازگردند.

شبکه‌های برق و آب

در طراحی و مدیریت شبکه‌های برق و آب، نیاز به بازدید و بررسی تمامی خطوط انتقال وجود دارد. گراف‌های اویلری به مهندسین کمک می‌کنند تا مسیرهای بهینه برای بازدید و نگهداری از این خطوط را طراحی کنند.

حل مسائل ریاضی و نظریه گراف

گراف‌های اویلری در حل مسائل ریاضی و نظریه گراف کاربرد دارند. این گراف‌ها به تحلیل و بررسی خواص مختلف گراف‌ها و ارتباطات بین رئوس و یال‌ها کمک می‌کنند.

گراف همیلتونی

گراف همیلتونی گرافی است که شامل یک دور (سیکل) همیلتونی باشد، یعنی مسیری که از هر راس دقیقاً یک بار عبور کند و به نقطه شروع بازگردد. اگر چنین مسیری در گراف وجود داشته باشد، گراف همیلتونی نامیده می‌شود.

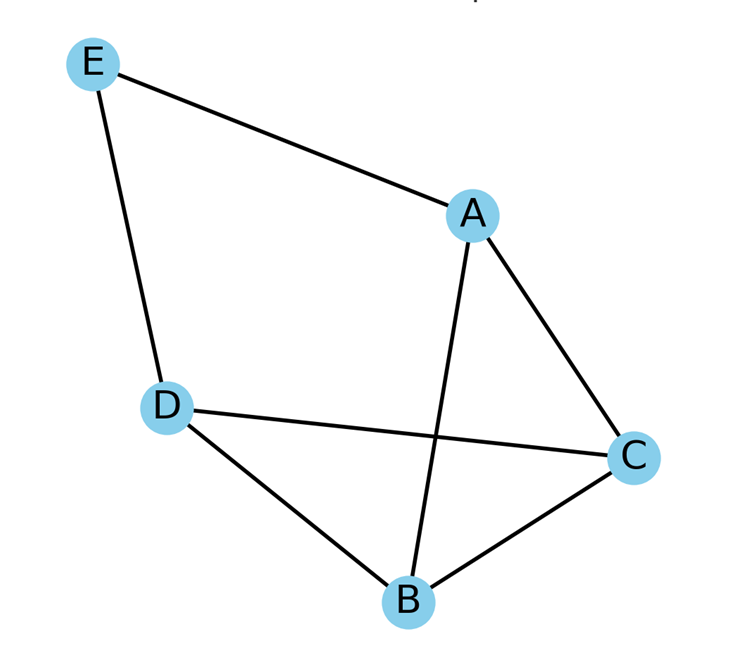
ویژگی‌های گراف همیلتونی

گراف همیلتونی ویژگی‌هایی دارد که در زیر به آن‌ها اشاره می‌کنیم:

مسیر همیلتونی

مسیر همیلتونی (Hamiltonian Path) مسیری در گراف است که هر راس را دقیقاً یک بار بازدید می‌کند، اما نیازی به بازگشت به راس ابتدایی نیست. به عبارت دیگر، مسیر همیلتونی از یک راس شروع شده، به تمام رئوس دیگر می‌رود و در یک راس متفاوت پایان می‌یابد.

دور همیلتونی

دور همیلتونی (Hamiltonian Cycle) یا چرخه همیلتونی نوع خاصی از مسیر همیلتونی است که در آن مسیر به راس ابتدایی بازمی‌گردد. این بدین معناست که دور همیلتونی از یک راس شروع کرده، هر راس را دقیقاً یک بار بازدید می‌کند و در پایان به همان راس شروع برمی‌گردد. وجود یک دور همیلتونی در گراف، آن را به یک گراف همیلتونی تبدیل می‌کند.

شناسایی گراف همیلتونی

شناسایی یک گراف همیلتونی چالش‌برانگیز است زیرا هیچ الگوریتم کلی و سریعی برای تعیین همیلتونی بودن گراف وجود ندارد. برخلاف گراف‌های اویلری که معیارهای مشخصی برای شناسایی دارند، برای گراف‌های همیلتونی باید بررسی دقیقی انجام شود. روش‌هایی مانند جستجوی جامع (Backtracking) یا استفاده از الگوریتم‌های تقریبی برای یافتن مسیرهای همیلتونی مورد استفاده قرار می‌گیرند.

کاربردهای گراف همیلتونی

گراف‌های همیلتونی در مسائل مختلفی از جمله موارد زیر کاربرد دارند:

مسائل مسیریابی و لجستیک

در مسائل مسیریابی و توزیع کالا، یافتن مسیرهایی که بهینه باشند و تمامی نقاط توزیع را پوشش دهند، مهم است. استفاده از گراف‌های همیلتونی می‌تواند به کاهش هزینه‌ها و افزایش کارایی کمک کند.

طراحی شبکه‌های توزیع

در طراحی شبکه‌های توزیع مانند شبکه‌های برق، آب و گاز، نیاز به بازدید از تمامی نقاط شبکه و بازگشت به نقطه شروع وجود دارد. استفاده از گراف همیلتونی در این موارد به بهینه‌سازی مسیرهای توزیع و کاهش هزینه‌ها کمک می‌کند.

مسئله فروشنده دوره‌گرد

یکی از معروف‌ترین مسائل بهینه‌سازی که از گراف‌های همیلتونی استفاده می‌کند، مسئله فروشنده دوره‌گرد (TSP) است. در این مسئله، یک فروشنده باید به چندین شهر سفر کند و به نقطه شروع بازگردد به گونه‌ای که مجموع مسافت طی شده حداقل باشد. مدل‌سازی این مسئله با استفاده از گراف همیلتونی به فروشنده کمک می‌کند تا کوتاه‌ترین مسیر ممکن را پیدا کند.

گراف‌ متصل

گراف متصل (همبند) گرافی است که در آن برای هر جفت راس یک مسیر وجود دارد که آن دو را به هم متصل می‌کند. به عبارت دیگر، در گراف متصل می‌توان از هر راس به هر راس دیگر با دنبال کردن یال‌ها رسید. توجه کنید که این تعریف برای گراف‌های همبند بدون جهت است. درمورد گراف‌های جهت‌دار، همبندی یعنی اگر جهت‌ها را نادیده بگیریم، حداقل یک مسیر بین هر دو راس وجود داشته باشد.

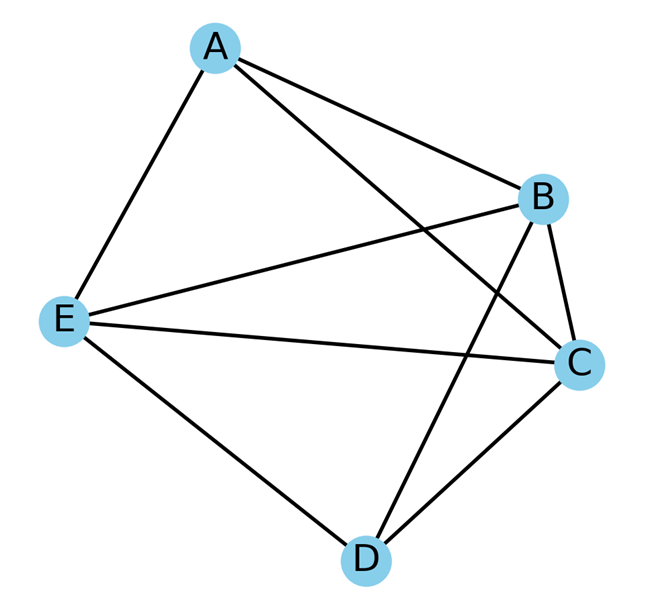
حداکثر تعداد یال‌ در گراف بدون جهت متصل

در یک گراف بدون جهت متصل با n راس، حداکثر تعداد یال‌ها زمانی است که گراف به صورت یک گراف کامل بدون جهت باشد. در این حالت، هر راس به تمامی n-1 راس دیگر متصل است، یعنی n(n-1) یال داریم اما چون جهت در این نوع گراف معنایی ندارد و یال بین هر دو راس را باید یک بار بشماریم، حاصل را تقسیم بر دو می‌کنیم. این یعنی بیشینه تعداد یال‌ها در این حالت برابر است با:

\large \frac{n(n-1)}{2}

حداکثر تعداد یال‌ در گراف جهت‌دار متصل

در یک گراف جهت‌دار متصل با n راس، حداکثر تعداد یال‌ها زمانی است که گراف به صورت یک گراف کامل جهت‌دار باشد. در این حالت، هر راس به تمامی n-1 راس دیگر متصل است و به‌همین دلیل بیشینه تعداد یال‌ها در این حالت برابر است با:

\large n(n-1)

کاربردهای گراف متصل

درادامه به بررسی برخی از کاربردهای گراف‌های متصل می‌پردازیم:

طراحی و بهینه‌سازی شبکه

در طراحی شبکه‌های کامپیوتری و مخابراتی، مدل‌سازی گراف‌های متصل به طراحان کمک می‌کند تا اطمینان حاصل کنند که تمامی دستگاه‌ها و سرورها به یکدیگر متصل هستند. این مدل‌سازی به بهینه‌سازی توپولوژی شبکه و کاهش تأخیر و افزایش پهنای باند کمک می‌کند.

مدیریت شبکه

در مدیریت شبکه، استفاده از گراف‌های متصل به مدیران شبکه کمک می‌کند تا به سرعت نقاط قطعی و مشکلات ارتباطی را شناسایی و رفع کنند. این امر به افزایش پایداری و قابلیت اطمینان شبکه کمک می‌کند.

شبکه‌های حسگر بی‌سیم

در شبکه‌های حسگر بی‌سیم، اتصال کامل بین حسگرها برای جمع‌آوری و انتقال داده‌ها بسیار مهم است. گراف‌های متصل به بهینه‌سازی مسیرهای ارتباطی و کاهش مصرف انرژی کمک می‌کنند.

گراف نامتصل

گراف نامتصل (ناهمبند) گرافی است که حداقل یک جفت راس وجود دارد که هیچ مسیری آن‌ها را به هم متصل نمی‌کند.  به عبارت دیگر، در گراف نامتصل برخی از رئوس به هیچ طریق نمی‌توانند به برخی دیگر از رئوس دسترسی داشته باشند. گراف نامتصل از چندین جزء متصل تشکیل شده است.

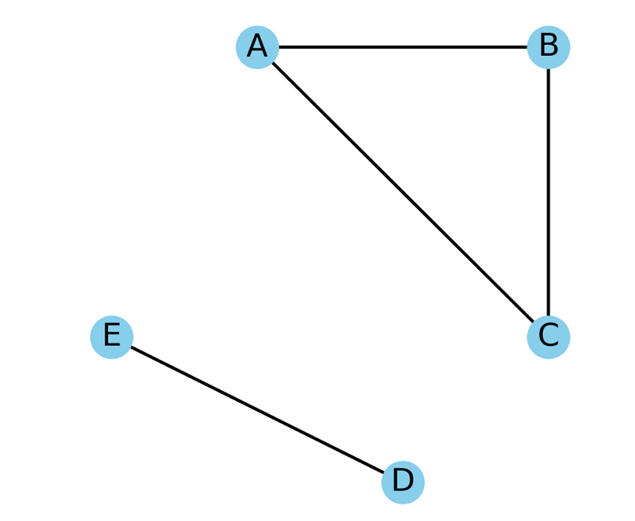
کاربردهای گراف نامتصل

درادامه به بررسی برخی از کاربردهای گراف‌های نامتصل می‌پردازیم:

تشخیص و تحلیل خرابی‌ها

در شبکه‌های ارتباطی، مانند شبکه‌های کامپیوتری و مخابراتی، اتصال پایدار بین دستگاه‌ها و سرورها بسیار مهم است. اگر بخشی از شبکه به دلایلی مانند خرابی سخت‌افزار، قطع کابل‌ها یا مشکلات نرم‌افزاری قطع شود، گراف شبکه نامتصل می‌شود. با تحلیل این گراف‌های نامتصل می‌توان نقاط ضعف و خرابی‌ها را شناسایی کرد و برای بهبود و تعمیر شبکه اقدام کرد.

سیستم‌های تولیدی

در برخی صنایع، نیاز به مدل‌سازی و تحلیل خطوط تولید مجزا وجود دارد. هر خط تولید می‌تواند به عنوان یک جزء متصل مستقل در یک گراف نامتصل مدل‌سازی شود. این مدل‌سازی به تحلیل و بهینه‌سازی عملکرد هر خط تولید کمک می‌کند.

گراف‌ مسطح

گراف مسطح (Planar Graphs) گرافی است که می‌توان آن را بر روی یک صفحه رسم کرد به گونه‌ای که هیچ دو یالی یکدیگر را قطع نکنند. به عبارت دیگر، یال‌های این گراف در صفحه به هم نمی‌خورند و تلاقی ندارند.

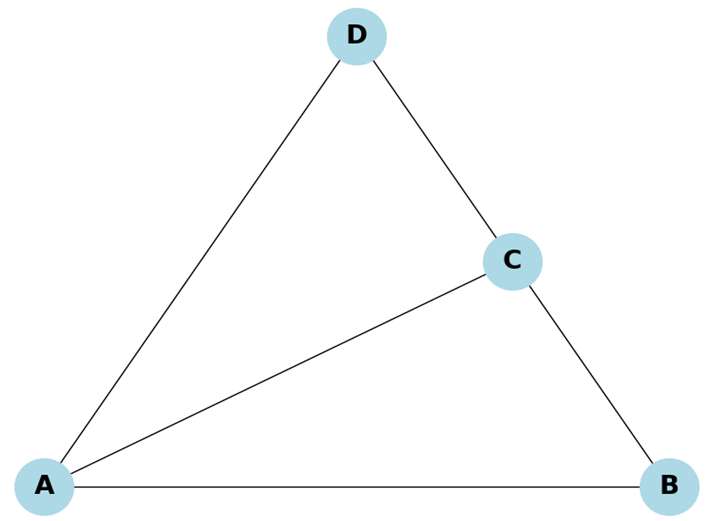
ویژگی‌های گراف‌ مسطح

گراف مسطح ویژگی‌های منحصربه‌فردی دارد که در زیر به آن‌ها اشاره می‌کنیم:

ناحیه

در گراف‌های مسطح، یک ناحیه (Region) به قسمتی از صفحه گفته می‌شود که توسط یال‌های گراف محصور شده باشد. نواحی شامل قسمت‌هایی از صفحه هستند که توسط یال‌ها به قسمت‌های کوچک‌تر تقسیم شده‌اند.

فرمول اویلر

برای یک گراف مسطح همبند با V راس، E یال و R ناحیه، فرمولی موسوم به فرمول اویلر به صورت زیر برقرار است:

\large R = E - V + 2

حداکثر تعداد یال‌ها

در یک گراف مسطح ساده با تعداد رئوس بیشتر یا مساوی ۳ رابطه زیر برقرار است:

\large E \leq 3V - 6

قضیه کوراتوفسکی

طبق قضیه کوراتوفسکی (Kuratowski’s theorem) اگر گرافی شامل زیرگراف K₅ یا K_3,3  به‌صورت جزیی نباشد، آن گراف مسطح است.

کاربردهای گراف مسطح

گراف مسطح کاربردهایی دارد که در زیر به آن‌ها می‌پردازیم:

طراحی مدارهای الکترونیکی

در طراحی مدارهای چاپی (Printed Circuit Board یا PCB)، از گراف‌های مسطح به عنوان یک ابزار موثر برای اطمینان از عدم تلاقی و تداخل بین خطوط مسی استفاده می‌شود. مدارهای چاپی بخش‌های پیچیده‌ای از دستگاه‌های الکترونیکی هستند که نیاز به طراحی دقیق و بهینه دارند.

طراحی شبکه‌های ارتباطی

در طراحی شبکه‌های ارتباطی بدون تداخل و تلاقی، از گراف‌های مسطح بهره گرفته می‌شود. مثلا در طراحی نقشه‌های مترو که در آن ایستگاه‌ها به عنوان راس و خطوط مترو به عنوان یال‌ها در نظر گرفته می‌شوند و خطوط نباید یکدیگر را قطع کنند، از گراف‌های مسطح و ویژگی‌های آن استفاده می‌شود. همچنین در طراحی شبکه‌های آب و فاضلاب شهری که باید به گونه‌ای طراحی شوند که لوله‌ها یکدیگر را قطع نکنند این گراف‌ها مورد استفاده قرار می‌گیرند.

درخت‌

درخت (Tree) یک گراف همبند بدون دور (حلقه) است. همبند بودن درخت‌ها باعث می‌شود، هر دو راس با یک مسیر یکتا به هم متصل هستند. بدون دور بودن درخت‌ها نیز به این معنی است که هیچ مسیری وجود ندارد که از یک راس شروع شده و به همان راس بازگردد بدون اینکه یال‌ها تکرار شوند. این ویژگی‌ها درخت‌ها را به ساختارهای بسیار منظم و قابل پیش‌بینی تبدیل می‌کند.

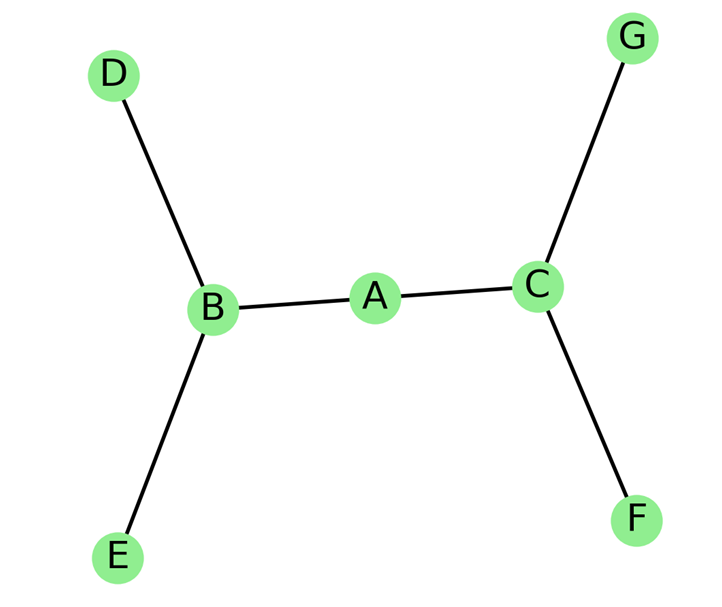
ویژگی‌های درخت

درخت‌ها ویژگی‌های منحصربه‌فردی دارند که در ادامه آن‌ها را بررسی می‌کنیم:

تعداد یال‌ها

یک درخت با n راس، دارای n-1 یال است. این ویژگی به این دلیل است که درخت‌ها بدون دور هستند و اضافه کردن هر یال اضافی باعث ایجاد یک دور می‌شود. تعداد یال‌های کمتر در درخت‌ها نشان‌دهنده ساختار ساده‌تر و منظم‌تر آن‌ها است.

اتصال با یک مسیر یکتا

در درخت‌ها، بین هر دو راس دقیقاً یک مسیر یکتا وجود دارد. این ویژگی باعث می‌شود که درخت‌ها ساختارهای بسیار منظم و پیش‌بینی‌پذیر باشند. این خاصیت درخت‌ها را از گراف‌های دیگر که ممکن است دارای مسیرهای متعدد بین دو راس باشند، متمایز می‌کند.

درخت‌های ریشه‌دار

در درخت‌های ریشه‌دار، یک راس به عنوان ریشه در نظر گرفته می‌شود و تمام یال‌ها جهت‌دار هستند و از ریشه به سمت برگ‌ها جریان دارند. این ساختار سلسله‌مراتبی به سازمان‌دهی و تجزیه و تحلیل داده‌ها کمک می‌کند.

کاربردهای درخت

درادامه به بررسی برخی از کاربردهای درخت می‌پردازیم:

ساختارهای داده در علوم کامپیوتر

درخت‌ها به طور گسترده‌ای در ساختارهای داده مانند درخت‌های جستجوی دودویی، درخت‌های AVL و درخت‌های B استفاده می‌شوند. این ساختارها به بهینه‌سازی عملیات مختلف مانند جستجو، درج و حذف کمک می‌کنند.

• درخت‌های جستجوی دودویی (Binary Search Trees): این درخت‌ها به گونه‌ای طراحی شده‌اند که عملیات جستجو، درج و حذف عناصر به صورت بهینه انجام شود. در این درخت‌ها، هر گره دارای حداکثر دو فرزند است و گره‌های زیرین به گونه‌ای مرتب شده‌اند که عملیات جستجو به سادگی انجام شود.

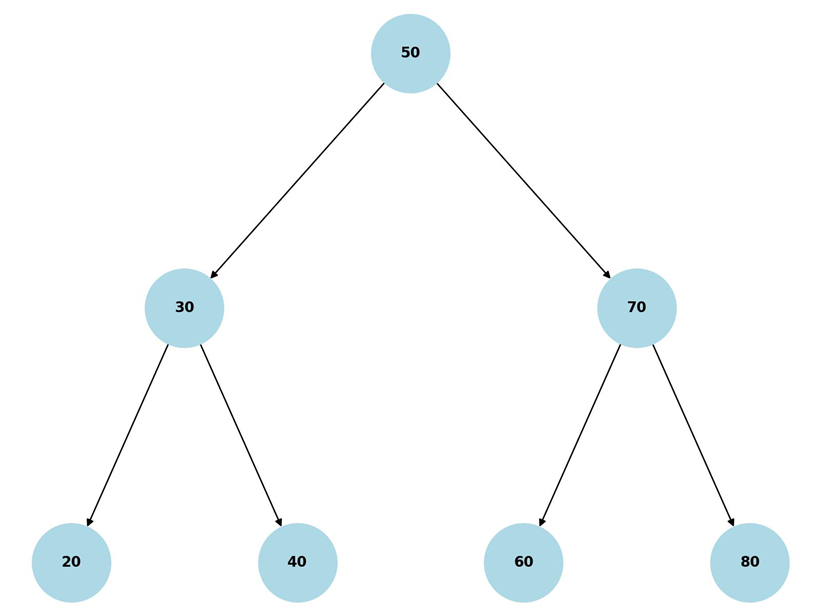
• درخت‌های AVL: این درخت‌ها نوعی درخت جستجوی دودویی متوازن هستند که به طور خودکار توازن خود را حفظ می‌کند. یعنی اختلاف ارتفاع زیر درخت‌های هر گره آن حداکثر یک واحد است. این ویژگی باعث می‌شود که عملیات جستجو، درج و حذف در آن‌ها همواره در زمان O(logn) انجام شود.

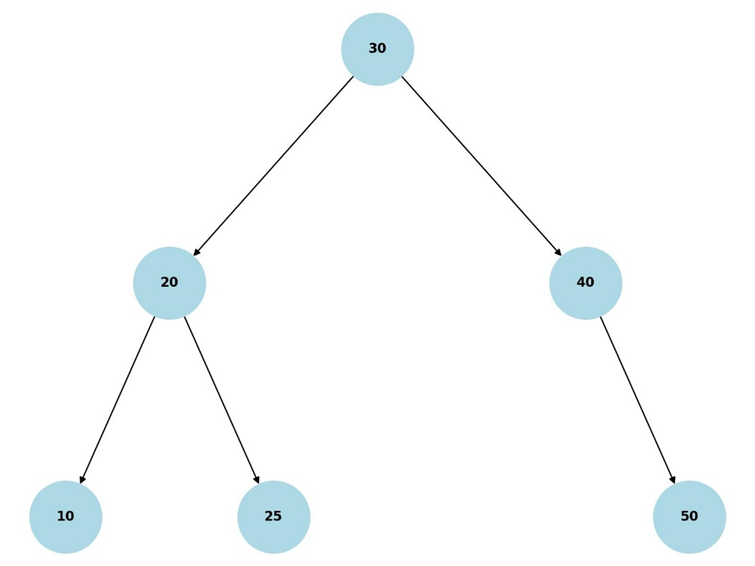
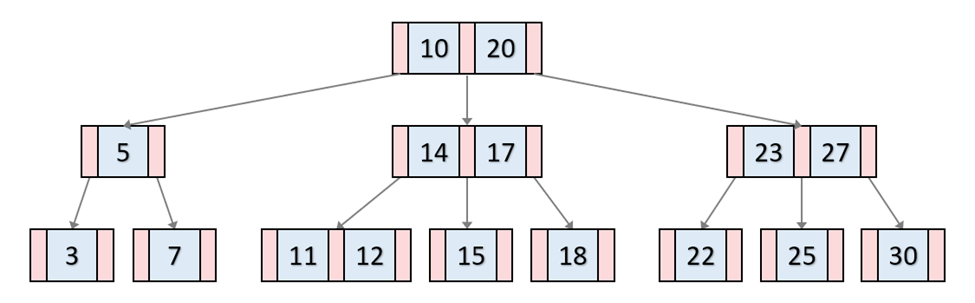
• درخت‌های B: این نوع درخت‌ها، بیشتر در سیستم‌های مدیریت پایگاه داده مورد استفاده قرار می‌گیرند و به بهینه‌سازی عملیات جستجو و دسترسی به داده‌ها در پایگاه‌های داده بزرگ کمک می‌کنند.

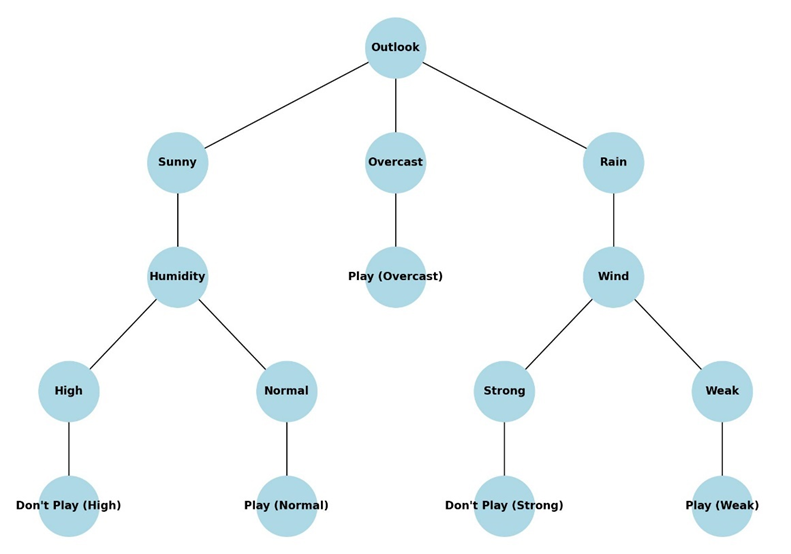
درخت‌های تصمیم‌گیری

درخت‌های تصمیم‌گیری (Decision Trees) برای تصمیم‌گیری و طبقه‌بندی داده‌ها بر اساس ویژگی‌های مختلف استفاده می‌شوند. هر درخت تصمیم‌گیری یک ساختار سلسله‌مراتبی است که داده‌ها را بر اساس معیارهای مختلف تجزیه و تحلیل می‌کند. درنهایت مجموعه این درخت‌ها که یک جنگل را تشکیل می‌‌دهند، نتیجه نهایی را مشخص خواهند کرد.

شبکه‌های ارتباطی

درخت‌ها برای مدل‌سازی و طراحی شبکه‌های ارتباطی نیز استفاده می‌شوند که در آن‌ها نیاز به یک ساختار سلسله‌مراتبی برای مسیریابی و مدیریت ترافیک وجود دارد.

• شبکه‌های محلی (LAN): درخت‌ها برای طراحی و مدیریت توپولوژی شبکه‌های محلی استفاده می‌شوند. در این شبکه‌ها، روترها و سوئیچ‌ها به گونه‌ای متصل می‌شوند که یک ساختار درختی تشکیل دهند که به بهینه‌سازی مسیریابی و کاهش تراکم ترافیک کمک می‌کند.
• شبکه‌های بی‌سیم: در شبکه‌های بی‌سیم، از درخت‌ها برای سازمان‌دهی و مدیریت اتصال دستگاه‌ها به یکدیگر استفاده می‌شود. این ساختار سلسله‌مراتبی به بهبود کارایی شبکه و کاهش مصرف انرژی کمک می‌کند.

سیستم‌های سلسله‌مراتبی

درخت‌ها برای مدل‌سازی سیستم‌های سلسله‌مراتبی مانند سازمان‌ها، طبقه‌بندی‌ها و سلسله‌مراتب فایل‌ها در سیستم‌های عامل استفاده می‌شوند.

• سازمان‌ها و شرکت‌ها: درخت‌ها به مدل‌سازی ساختار سازمانی و روابط بین مدیران، کارکنان و دپارتمان‌ها کمک می‌کنند. این مدل‌سازی به تحلیل و بهبود ارتباطات و فرآیندهای کاری در سازمان‌ها کمک می‌کند.
• طبقه‌بندی‌ها: درخت‌ها برای مدل‌سازی طبقه‌بندی‌های مختلف مانند دسته‌بندی محصولات، گونه‌های زیستی و دسته‌بندی‌های علمی استفاده می‌شوند.
• سلسله‌مراتب فایل‌ها: در سیستم‌های عامل، فایل‌ها و پوشه‌ها به صورت درختی سازماندهی می‌شوند. این ساختار به کاربران و سیستم‌عامل اجازه می‌دهد که فایل‌ها را به سادگی جستجو، دسترسی و مدیریت کنند.

جنگل

جنگل‌ها مجموعه‌ای از درخت‌ها هستند که در آن‌ها هیچ دوری (حلقه‌ای) وجود ندارد. هر جنگل از چندین درخت مجزا تشکیل شده است که هر کدام به عنوان یک زیرگراف متصل مستقل عمل می‌کنند. جنگل‌ها به دلیل ویژگی‌های خاص خود در بسیاری از کاربردهای علمی و عملی استفاده می‌شوند.

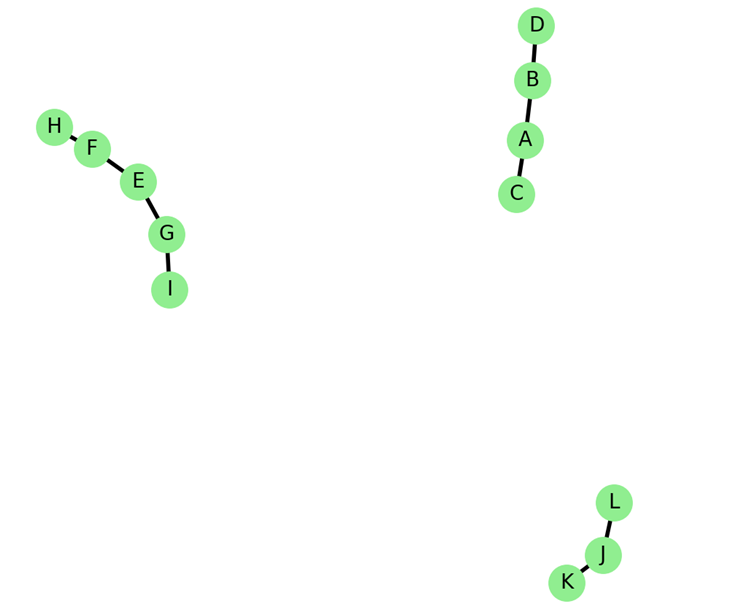
ویژگی‌های جنگل

در زیر به توضیح بیشتر در مورد ویژگی‌های جنگل‌ها می‌پردازیم:

تعداد یال‌ها

اگر جنگلی دارای n راس و k درخت باشد، تعداد یال‌های آن برابر با n-k است. این ویژگی به این دلیل است که هر درخت دارای ni – 1 یال است که ni تعداد رئوس آن درخت است. درواقع اگر مجموع رئوس را n در نظر بگیریم، خواهیم داشت:

\large n = n_1 + n_2 + \ldots + n_k

و مجموع یال‌ها برابر است با:

\large (n_1 - 1) + (n_2 - 1) + \ldots + (n_k - 1)

که می‌توان آن را به صورت زیر ساده کرد:

\large (n_1 + n_2 + \ldots + n_k) - k = n - k

زیرگراف‌های متصل

هر زیرگراف متصل از یک جنگل، خود یک درخت است. این ویژگی باعث می‌شود که تجزیه و تحلیل بخش‌های مختلف یک جنگل به راحتی انجام شود و هر زیرگراف متصل به عنوان یک ساختار مستقل مورد بررسی قرار گیرد.

کاربردهای جنگل

در ادامه کاربردهای جنگل را بررسی می‌کنیم:

جنگل‌های تصادفی

جنگل‌ها در ساختارهای داده پیشرفته مانند جنگل‌های تصادفی استفاده می‌شوند. این ساختارها به بهبود کارایی و دقت در تحلیل و پردازش داده‌ها کمک می‌کنند. جنگل‌های تصادفی (Random Forests) در الگوریتم‌های یادگیری ماشین برای مدل‌سازی و پیش‌بینی استفاده می‌شوند. جنگل‌های تصادفی از مجموعه‌ای از درخت‌های تصمیم‌گیری تشکیل شده‌اند که به صورت تصادفی ایجاد می‌شوند.

مدل‌سازی سیستم‌های غیرمتصل

در برخی موارد، نیاز است که سیستم‌های مجزا و مستقل از یکدیگر مدل‌سازی شوند و جنگل‌ها برای این نوع مدل‌سازی مناسب هستند.

• سیستم‌های تولیدی: در صنایع تولیدی، خطوط تولید مجزا و مستقل به صورت جنگل مدل‌سازی می‌شوند. هر خط تولید به عنوان یک درخت مستقل در جنگل عمل می‌کند.
• شبکه‌های توزیع: در شبکه‌های توزیع کالا و خدمات، شبکه‌های توزیع محلی و منطقه‌ای به صورت جنگل مدل‌سازی می‌شوند. هر شبکه توزیع به عنوان یک درخت مستقل در جنگل عمل می‌کند.

این تنوع در انواع گراف‌ها نشان می‌دهد که چگونه می‌توانیم با استفاده از ساختارهای گرافی مختلف، مسائل پیچیده را مدل‌سازی و تحلیل کنیم. هر نوع گراف با ویژگی‌ها و خصوصیات خاص خود می‌تواند به حل مسائل مختلف در حوزه‌های گوناگون کمک کند و ابزار قدرتمندی برای مدل‌سازی و تحلیل سیستم‌های پیچیده فراهم کند.

گراف‌ همگن

گراف‌های همگن (Homogeneous graphs)، گراف‌هایی هستند که تمامی راس‌ها و یال‌های آن‌ها از یک نوع و دارای خصوصیات یکسانی هستند. به عبارت دیگر، در گراف‌های همگن، نوع و ویژگی‌های تمامی عناصر (راس‌ها و یال‌ها) مشابه هستند و هیچ تفاوتی بین آن‌ها وجود ندارد.

ویژگی‌های گراف همگن

در ادامه به توضیح بیشتر در مورد ویژگی‌های گراف همگن می‌پردازیم:

یکنواختی راس‌ها

در گراف‌های همگن، راس‌ها دارای ویژگی‌های یکسانی هستند. این ویژگی‌ها می‌توانند شامل موارد زیر باشند:

• نوع راس‌ها: تمامی راس‌ها از یک نوع هستند و هیچ راسی با ویژگی یا رفتار متفاوت وجود ندارد.
• درجه راس‌ها: تعداد یال‌های متصل به هر راس (درجه راس) در یک گراف همگن یکسان است، به این معنا که همه راس‌ها تعداد مشابهی از یال‌ها دارند.
• وزن راس‌ها: اگر گراف وزن‌دار باشد، وزن اختصاص داده شده به تمامی راس‌ها یکسان است.

یکنواختی یال‌ها

یال‌ها نیز در گراف‌های همگن دارای ویژگی‌های یکسانی هستند. این ویژگی‌ها می‌توانند شامل موارد زیر باشند:

• نوع یال‌ها: تمامی یال‌ها از یک نوع هستند؛ به عنوان مثال، همه یال‌ها مستقیم (بدون جهت) یا جهت‌دار (با جهت مشخص) هستند.
• وزن یال‌ها: اگر گراف وزن‌دار باشد، تمامی یال‌ها وزن یکسانی دارند. به عبارت دیگر، هزینه یا فاصله‌ی مرتبط با هر یال برابر است.
• طول یال‌ها: در گراف‌های فضایی یا شبکه‌های فیزیکی، طول یا فاصله‌ی هر یال بین دو راس برابر است.

کاربردهای گراف همگن

در این بخش کاربردهای گراف همگن را بررسی می‌کنیم:

شبکه‌های اجتماعی ساده

در شبکه‌های اجتماعی ساده که روابط بین کاربران به شکل یکسانی تعریف شده است، از گراف‌های همگن استفاده می‌شود. به عنوان مثال، یک شبکه دوستانه که همه کاربران با یک نوع رابطه (مثلاً دوستی) به هم متصل هستند.

مدل‌سازی مسائل مسیریابی

در مسائل مسیریابی ابتدایی مانند یافتن کوتاه‌ترین مسیر در یک نقشه ساده که همه جاده‌ها ویژگی‌های مشابهی دارند، گراف‌های همگن به کار می‌روند.

شبکه‌های ارتباطی

در شبکه‌های ارتباطی ساده که تمامی لینک‌ها و دستگاه‌ها (راس‌ها) خصوصیات یکسانی دارند، از گراف‌های همگن استفاده می‌شود. مانند یک شبکه محلی (LAN) که تمامی دستگاه‌ها و کابل‌ها مشابه هستند.

گراف‌های ناهمگن

گراف‌های ناهمگن (Heterogeneous graphs)، گراف‌هایی هستند که راس‌ها و یال‌های آن‌ها می‌توانند دارای انواع و ویژگی‌های مختلفی باشند. این نوع گراف‌ها پیچیدگی بیشتری دارند زیرا عناصر آن‌ها متفاوت هستند و ممکن است روابط مختلفی بین آن‌ها وجود داشته باشد.

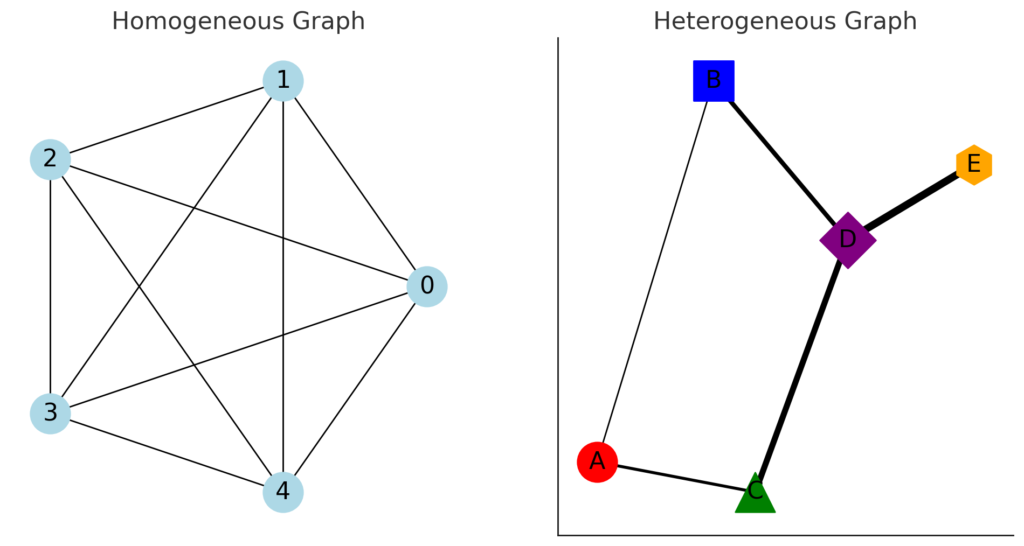
ویژگی‌های گراف ناهمگن

در ادامه به توضیح بیشتر در مورد ویژگی‌های گراف ناهمگن می‌پردازیم:

تنوع راس‌ها

راس‌ها در گراف‌های ناهمگن می‌توانند دارای ویژگی‌ها و خصوصیات متفاوتی باشند. این ویژگی‌ها می‌توانند شامل موارد زیر باشند:

• نوع راس‌ها: راس‌ها می‌توانند از انواع مختلفی باشند. به عنوان مثال، در یک شبکه اجتماعی، راس‌ها می‌توانند نمایانگر افراد، گروه‌ها، صفحات، و محتواهای مختلف باشند.
• وزن راس‌ها: در برخی گراف‌ها، هر راس می‌تواند وزنی داشته باشد که نشان‌دهنده اهمیت یا تأثیر آن راس است. به عنوان مثال، در یک گراف شبکه ترافیکی، یک رأس می‌تواند نشان‌دهنده یک شهر باشد و وزن آن تعداد جمعیت آن شهر را نشان دهد.
• ویژگی‌های راس‌ها: راس‌ها می‌توانند دارای ویژگی‌های مختلفی باشند مانند سن، جنسیت، موقعیت جغرافیایی و دیگر خصوصیات. این ویژگی‌ها می‌توانند در تحلیل و مدل‌سازی گراف نقش مهمی ایفا کنند.

تنوع یال‌ها

یال‌ها نیز در گراف‌های ناهمگن می‌توانند دارای ویژگی‌ها و خصوصیات مختلفی باشند:

• نوع یال‌ها: یال‌ها می‌توانند از انواع مختلفی باشند؛ به عنوان مثال، یال‌های جهت‌دار و بدون جهت، یا یال‌های مستقیم و غیرمستقیم. در یک گراف شبکه حمل و نقل، یال‌ها می‌توانند نمایانگر مسیرهای جاده‌ای، خطوط هوایی، یا مسیرهای ریلی باشند.
• وزن یال‌ها: یال‌ها می‌توانند دارای وزن‌های مختلفی باشند که نشان‌دهنده هزینه یا فاصله بین دو راس است. به عنوان مثال، در یک گراف ارتباطات، وزن یال‌ها می‌تواند نشان‌دهنده قدرت سیگنال یا هزینه تماس بین دو دستگاه باشد.
• ویژگی‌های یال‌ها: یال‌ها می‌توانند ویژگی‌های مختلفی مانند ظرفیت، تأخیر، یا پهنای باند داشته باشند. این ویژگی‌ها می‌توانند در تحلیل شبکه‌های ارتباطی یا حمل و نقل بسیار مهم باشند.

کاربردهای گراف ناهمگن

در این بخش کاربردهای گراف ناهمگن را بررسی می‌کنیم:

شبکه‌های اجتماعی پیچیده

در شبکه‌های اجتماعی پیچیده که انواع مختلفی از روابط بین کاربران وجود دارد، از گراف‌های ناهمگن استفاده می‌شود. به عنوان مثال، یک شبکه اجتماعی که شامل کاربران، گروه‌ها، صفحات و محتواهای مختلف با روابط متنوع است.

مدل‌های بیولوژیکی

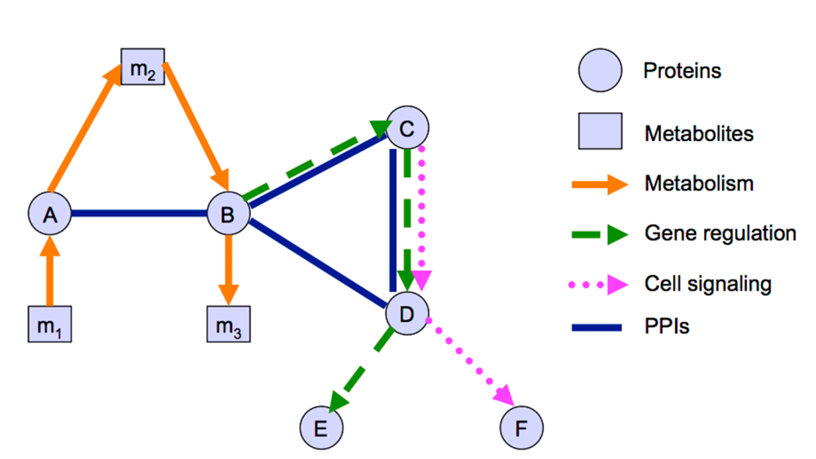
در مدل‌های بیولوژیکی مانند شبکه‌های ژنی و پروتئینی که انواع مختلفی از مولکول‌ها و تعاملات بین آن‌ها وجود دارد، از گراف‌های ناهمگن استفاده می‌شود. به عنوان مثال، در یک شبکه ژنی، راس‌ها می‌توانند نمایانگر ژن‌ها، پروتئین‌ها و متابولیت‌ها باشند.

تحلیل بازار

در تحلیل بازار که شامل انواع مختلفی از محصولات، مشتریان و تعاملات بین آن‌ها است، از گراف‌های ناهمگن استفاده می‌شود. به عنوان مثال، در یک بازار آنلاین، رأس‌ها می‌توانند نمایانگر محصولات، فروشندگان و خریداران با روابط خرید و فروش باشند.

سیستم‌های توصیه‌گر

در سیستم‌های توصیه‌گر که نیاز به مدل‌سازی روابط پیچیده بین کاربران و آیتم‌ها دارند، از گراف‌های ناهمگن استفاده می‌شود. به عنوان مثال، در یک سیستم توصیه فیلم، رأس‌ها می‌توانند نمایانگر کاربران، فیلم‌ها، ژانرها و کارگردانان باشند.

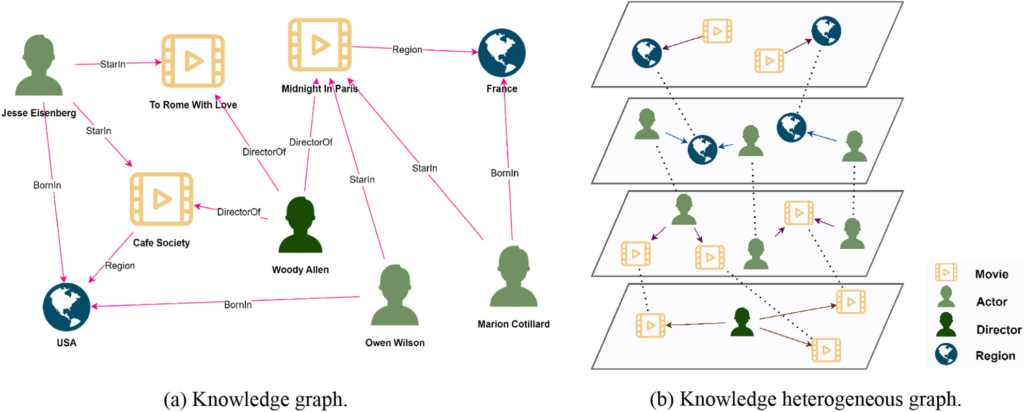
جمع‌بندی انواع گراف

در جدول زیر می‌توانید به‌طور خلاصه مطالب گفته‌شده درباره نظریه گراف را ببینید:

نوع گراف	ویژگی‌ها	کاربردها
گراف ساده	بدون یال‌های تکراری و طوقه	مدل‌سازی روابط ساده
گراف جهت‌دار	دارای جهت در یال‌ها	مدل‌سازی جریان‌ها و روابط جهت‌دار مانند شبکه‌های اجتماعی
گراف وزن‌دار	دارای وزن برای یال‌ها	مسیریابی و بهینه‌سازی هزینه‌ها در شبکه‌های حمل و نقل و ارتباطی
گراف چندگانه	امکان وجود یال‌های موازی بین دو راس	مدل‌سازی شبکه‌های پیچیده مانند مسیرهای متعدد بین دو نقطه
گراف کامل	اتصال تمامی جفت رئوس با یک یال	طراحی مدارهای الکترونیکی
گراف دو بخشی	تقسیم رئوس به دو مجموعه مجزا	مدل‌سازی تطابق‌ها مانند تخصیص کارها به کارمندان
گراف اویلری	دارای مدار اویلری	طراحی مسیرهای خدماتی
گراف همیلتونی	دارای دور همیلتونی	مسیریابی و بهینه‌سازی مسیرها مانند مسئله فروشنده دوره‌گرد
گراف همبند	وجود حداقل یک مسیر بین هر دو راس	طراحی و مدیریت شبکه‌های ارتباطی
گراف ناهمبند	عدم وجود مسیر بین حداقل دو راس	تحلیل و شناسایی خرابی‌ها در شبکه‌ها
درخت	گراف همبند بدون دور	ساختارهای داده‌ای مانند درخت‌های جستجو
جنگل	مجموعه‌ای از درخت‌ها	مدل‌سازی سیستم‌های غیر متصل و مستقل
گراف مسطح	امکان رسم گراف روی صفحه  بدون تلاقی یال‌ها	نقشه‌کشی متروها
گراف همگن	تمامی رئوس و یال‌ها دارای نوع یکسان	مدل‌سازی مسائل مسیریابی
گراف ناهمگن	رئوس و یال‌ها دارای انواع مختلف	مدل‌های بیولوژیکی

الگوریتم‌های مهم در نظریه گراف

در نظریه گراف، الگوریتم‌های متعددی برای حل مسائل مختلف وجود دارد که از مهم‌ترین آن‌ها می‌توان به موارد زیر اشاره کرد.

الگوریتم بلمن-فورد

الگوریتم بلمن-فورد (Bellman–Ford algorithm) یکی از الگوریتم‌های مهم در نظریه گراف و علوم کامپیوتر است که برای یافتن کوتاه‌ترین مسیر از یک راس مبدأ به سایر رئوس در یک گراف وزن‌دار استفاده می‌شود. این الگوریتم به ویژه زمانی مفید است که گراف حاوی یال‌هایی با وزن منفی باشد، زیرا می‌تواند به درستی با این نوع یال‌ها برخورد کند و همچنین تشخیص دهد که آیا گراف دارای دور منفی است یا خیر.

الگوریتم دایجسترا

الگوریتم دایجسترا (Dijkstra’s algorithm) برای یافتن کوتاه‌ترین مسیر از یک راس شروع به تمام رئوس دیگر در یک گراف وزن‌دار با یال‌های غیرمنفی استفاده می‌شود. این الگوریتم از یک روش حریصانه استفاده می‌کند و به صورت تکراری عمل می‌کند.

الگوریتم فلوید-وارشال

الگوریتم فلوید-وارشال (Floyd-Warshall Algorithm) یکی از الگوریتم‌های مهم در نظریه گراف است که برای یافتن کوتاه‌ترین مسیرها بین تمامی زوج رئوس در یک گراف وزن‌دار استفاده می‌شود. این الگوریتم از تکنیک برنامه‌ریزی پویا (Dynamic Programming) بهره می‌برد و می‌تواند هم برای گراف‌های جهت‌دار و هم برای گراف‌های بدون جهت به‌کار رود.

الگوریتم کراسکال

الگوریتم کراسکال (Kruskal’s algorithm) برای یافتن درخت پوشای کمینه (Minimum Spanning Tree) یک گراف وزن‌دار استفاده می‌شود و از روش حریصانه بهره می‌برد. این الگوریتم با انتخاب یال‌ها به ترتیب از کمترین به بیشترین وزن عمل می‌کند و برای گراف‌های همبند و ناهمبند مناسب است.

الگوریتم پریم

الگوریتم پریم (Prim’s algorithm) نیز مانند کراسکال برای یافتن درخت پوشای کمینه یک گراف وزن‌دار استفاده می‌شود و از روش حریصانه بهره می‌برد. الگوریتم پریم از روش حریصانه برای ساختن درخت پوشای کمینه استفاده می‌کند، به این معنا که در هر مرحله یالی را انتخاب می‌کند که کمترین وزن را دارد و باعث ایجاد دور در درخت نمی‌شود.

 کاربردهای نظریه گراف

نظریه گراف کاربردهای گسترده‌ای در علوم مختلف دارد که در این بخش آن‌ها را بررسی خواهیم کرد:

کاربرد در شبکه‌های عصبی گرافی

شبکه‌های عصبی گرافی (Graph Neural Networks – GNN) یک دسته از مدل‌های یادگیری عمیق هستند که برای کار با داده‌های گرافی طراحی شده‌اند. برخلاف شبکه‌های عصبی سنتی که با داده‌های جدولی یا تصاویر سروکار دارند، GNN‌ها می‌توانند اطلاعات موجود در ساختار گراف‌ها را مستقیماً پردازش و تحلیل کنند. این ویژگی GNN‌ها را برای کاربردهای متنوع و پیچیده‌ای مناسب می‌سازد.

GNN‌ها بر پایه اصول شبکه‌های عصبی مکرر (RNN) و شبکه‌های عصبی پیچشی (CNN) ساخته شده‌اند، اما به جای داده‌های خطی یا شبکه‌های منظم، با داده‌های گرافی کار می‌کنند. هر گراف از گره‌ها (راس‌ها) و یال‌ها (لبه‌ها) تشکیل شده است. GNN‌ها اطلاعات را از گره‌ها و یال‌ها دریافت کرده و با استفاده از الگوریتم‌های خاص خود این اطلاعات را پردازش می‌کنند.

کاربرد در بیوانفورماتیک

در بیوانفورماتیک، نظریه گراف برای مدل‌سازی و تحلیل شبکه‌های ژنتیکی و پروتئینی استفاده می‌شود. این مدل‌ها می‌توانند روابط پیچیده بین ژن‌ها و پروتئین‌ها را نشان دهند و به فهم بهتر فرآیندهای بیولوژیکی کمک کنند. مثلا، در مطالعه شبکه‌های پروتئینی، گراف‌ها می‌توانند به شناسایی پروتئین‌های کلیدی و مسیرهای بیولوژیکی کمک کنند که در نتیجه می‌تواند به توسعه داروهای جدید منجر شود.

پیشنهاد می‌کنیم مقاله راهنمای کامل پیاده‌سازی الگوریتم‌ ژنتیک در پایتون را هم بخوانید.

در تحلیل شبکه‌های ژنتیکی، گراف‌ها می‌توانند ارتباطات میان ژن‌های مختلف را نشان دهند و به درک بهتر وراثت و بیماری‌های ژنتیکی کمک کنند. استفاده از گراف‌ها در بیوانفورماتیک می‌تواند به شناسایی هدف‌های دارویی، پیش‌بینی واکنش‌های دارویی و در نهایت به توسعه درمان‌های مؤثرتر کمک کند.

 کاربرد در مسیریابی شبکه

در شبکه‌های کامپیوتری و ارتباطی، گراف‌ها برای مسیریابی و یافتن کوتاه‌ترین مسیرها بین گره‌های مختلف استفاده می‌شوند. الگوریتم‌های نظریه گراف می‌توانند به بهبود کارایی و کاهش هزینه‌های مسیریابی کمک کنند. به عنوان مثال، الگوریتم دیکسترا می‌تواند برای یافتن کوتاه‌ترین مسیر در شبکه‌ای از سرورها استفاده شود که به بهینه‌سازی انتقال داده‌ها کمک می‌کند. همچنین، در شبکه‌های مخابراتی، گراف‌ها می‌توانند برای طراحی شبکه‌های بهینه و توزیع منابع استفاده شوند. علاوه بر این، در شبکه‌های حسگر بی‌سیم و شبکه‌های ادهاک موبایل، الگوریتم‌های مسیریابی مبتنی بر گراف می‌توانند به بهبود کارایی شبکه و کاهش تأخیر در انتقال داده‌ها کمک کنند.

 کاربرد در مهندسی برق و الکترونیک

در مهندسی برق و الکترونیک، گراف‌ها برای مدل‌سازی و تحلیل مدارهای الکتریکی استفاده می‌شوند. با استفاده از نظریه گراف می‌توان مدارهای پیچیده را به صورت ساده‌تری مدل‌سازی و تحلیل کرد. به عنوان مثال، با استفاده از گراف‌های جهت‌دار، می‌توان جریان‌های الکتریکی و ولتاژها را در یک مدار تحلیل و نقاط ضعف و قوت آن را شناسایی کرد.

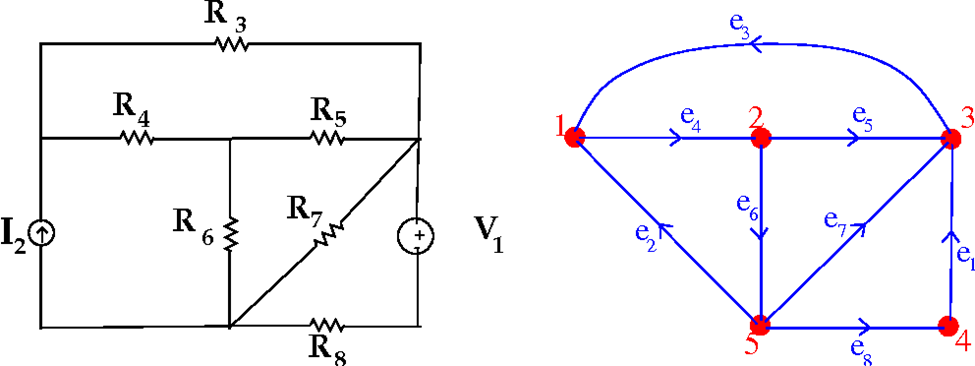
همچنین، با استفاده از گراف‌های وابستگی، می‌توان تعاملات بین عناصر مختلف مدار را مدل‌سازی و بهینه‌سازی کرد. این کاربردها می‌توانند به بهبود طراحی مدارها، کاهش مصرف انرژی و افزایش کارایی سیستم‌های الکتریکی کمک کنند.

 کاربرد در علوم کامپیوتر

در علوم کامپیوتر، نظریه گراف برای حل مسائل مختلف از جمله طراحی الگوریتم‌ها، بهینه‌سازی و تحلیل داده‌ها استفاده می‌شود. به عنوان مثال، الگوریتم‌های جستجوی گراف مانند الگوریتم جستجوی عمق‌اول (DFS) و الگوریتم جستجوی سطح‌اول (BFS) برای جستجو و مسیریابی در ساختارهای داده‌ای مختلف به کار می‌روند.

در تحلیل داده‌ها نیز گراف‌ها می‌توانند برای کشف الگوها و روابط پنهان بین داده‌ها استفاده شوند. به عنوان مثال، در تحلیل شبکه‌های ارتباطی، گراف‌ها می‌توانند به شناسایی گره‌های مهم و مسیرهای بحرانی کمک کنند. علاوه بر این، در یادگیری ماشین و هوش مصنوعی، گراف‌ها می‌توانند برای مدل‌سازی روابط پیچیده بین داده‌ها و بهبود دقت مدل‌های پیش‌بینی استفاده شوند.

 کاربرد در حمل و نقل و لجستیک

در حوزه حمل و نقل و لجستیک، نظریه گراف برای بهینه‌سازی مسیرها و کاهش هزینه‌ها استفاده می‌شود. به عنوان مثال، با استفاده از گراف‌ها می‌توان بهترین مسیرها برای حمل و نقل کالاها را تعیین کرد و به بهبود کارایی و کاهش زمان و هزینه‌های حمل و نقل کمک کرد.

در مدیریت زنجیره تامین، گراف‌ها می‌توانند برای مدل‌سازی و بهینه‌سازی جریان کالاها و اطلاعات بین نقاط مختلف زنجیره تامین استفاده شوند. استفاده از گراف‌ها در حمل و نقل می‌تواند به بهبود سیستم‌های حمل و نقل عمومی، کاهش تراکم ترافیک و بهبود زمان‌بندی سفرها کمک کند. همچنین، در حمل و نقل هوشمند، گراف‌ها می‌توانند برای مدل‌سازی و تحلیل شبکه‌های حمل و نقل و بهبود ایمنی و کارایی سیستم‌های حمل و نقل استفاده شوند.

به طور کلی، نظریه گراف به عنوان یک ابزار قدرتمند و چندکاربردی در علوم مختلف استفاده می‌شود و توانایی مدل‌سازی و تحلیل روابط پیچیده را به ما می‌دهد. این توانایی‌ها باعث شده است که گراف‌ها در بسیاری از حوزه‌ها به عنوان یک ابزار اساسی و ضروری مورد استفاده قرار گیرند.

پژوهش‌های جدید در حوزه نظریه گراف

پژوهش‌های جدید در نظریه گراف به بررسی مسائل پیچیده‌تر و کاربردهای نوین این نظریه در علوم مختلف می‌پردازند. از جمله این پژوهش‌ها می‌توان به تحلیل شبکه‌های پیچیده، کاربردهای هوش مصنوعی و یادگیری ماشین در گراف‌ها اشاره کرد. این تحقیقات می‌توانند به توسعه الگوریتم‌ها و مدل‌های جدید برای حل مسائل مختلف کمک کنند. به عنوان مثال، استفاده از نظریه گراف در تحلیل داده‌های بزرگ و شبکه‌های پیچیده می‌تواند به بهبود روش‌های تحلیل و پیش‌بینی کمک کند.

جمع‌بندی

نظریه گراف یکی از شاخه‌های پرکاربرد و تاثیرگذار در ریاضیات و علوم کامپیوتر است که به مطالعه گراف‌ها و ویژگی‌های آن‌ها می‌پردازد. این نظریه به دلیل توانایی بالا در مدل‌سازی و تحلیل روابط پیچیده در دنیای واقعی، به یکی از ابزارهای اصلی در حل مسائل مختلف علمی و عملی تبدیل شده است. از شبکه‌های اجتماعی گرفته تا بیوانفورماتیک، مهندسی برق و الکترونیک، و حتی مسائل مسیریابی و لجستیک، نظریه گراف نقش کلیدی در بهینه‌سازی و تحلیل سیستم‌ها ایفا می‌کند.

در این مقاله، ما به بررسی تاریخچه، مفاهیم پایه‌ای و پیشرفته، انواع گراف‌ها، و الگوریتم‌های مهم در نظریه گراف پرداختیم. همچنین کاربردهای گسترده این نظریه در حوزه‌های مختلف علمی و صنعتی مورد بحث قرار گرفت. پژوهش‌های جدید نشان می‌دهد که نظریه گراف همچنان در حال توسعه است و با استفاده از هوش مصنوعی و یادگیری ماشین، پتانسیل‌های بیشتری برای حل مسائل پیچیده و تحلیل داده‌های بزرگ فراهم می‌شود.

به طور کلی، فهم و تسلط بر نظریه گراف می‌تواند ابزارهای موثری برای تحلیل و بهینه‌سازی سیستم‌های پیچیده فراهم کند و به پیشرفت‌های علمی و فناوری‌های نوین کمک کند. این نظریه به عنوان یک زبان مشترک برای مدل‌سازی و تحلیل در بسیاری از حوزه‌ها، از اهمیت ویژه‌ای برخوردار است و پژوهش‌ها و کاربردهای جدید آن به ما امکان می‌دهد تا از این ابزار قدرتمند به بهترین نحو استفاده کنیم.

سوالات متداول

نظریه گراف چیست؟

نظریه گراف شاخه‌ای از ریاضیات است که به مطالعه گراف‌ها و خواص آن‌ها می‌پردازد. گراف‌ها شامل مجموعه‌ای از راس‌ها و یال‌ها هستند که این راس‌ها را به هم متصل می‌کنند. این نظریه برای مدل‌سازی و تحلیل ساختارهای پیچیده مورد استفاده قرار می‌گیرد.

گراف همیلتونی چیست؟

گراف همیلتونی گرافی است که شامل مسیری باشد که از هر راس دقیقا یک بار عبور کند و به نقطه شروع بازگردد. این نوع گراف‌ها در مسائل سفر فروشنده و بهینه‌سازی مسیرها کاربرد دارند و می‌توانند به پیدا کردن بهترین مسیر در شرایط مختلف کمک کنند.

کاربردهای نظریه گراف کدامند؟

کاربردهای نظریه گراف شامل تحلیل شبکه‌های اجتماعی، بیوانفورماتیک و مسیریابی شبکه‌های کامپیوتری است. این نظریه می‌تواند به فهم بهتر روابط پیچیده و بهینه‌سازی فرآیندها کمک کند و در حوزه‌های مختلف از جمله علوم اجتماعی، زیست‌شناسی و مهندسی مورد استفاده قرار گیرد.

الگوریتم دایجسترا چیست؟

الگوریتم دایجسترا برای یافتن کوتاه‌ترین مسیر از یک راس به تمام راس‌های دیگر در یک گراف وزن‌دار استفاده می‌شود. این الگوریتم برای مسائل مسیریابی و بهینه‌سازی کاربرد دارد و می‌تواند به بهبود کارایی و کاهش هزینه‌ها در شبکه‌های ارتباطی کمک کند.

چگونه می‌توان از نظریه گراف در مهندسی برق و الکترونیک استفاده کرد؟

در مهندسی برق و الکترونیک، گراف‌ها برای مدل‌سازی و تحلیل مدارهای الکتریکی استفاده می‌شوند. با استفاده از گراف‌های جهت‌دار، می‌توان جریان‌های الکتریکی و ولتاژها را در یک مدار تحلیل و نقاط ضعف و قوت آن را شناسایی کرد. این تحلیل‌ها می‌توانند به بهبود طراحی مدارها، کاهش مصرف انرژی و افزایش کارایی سیستم‌های الکتریکی کمک کنند.