همگرایی و واگرایی در سری ها یکی از مباحث مهم ریاضی عمومی است. موفقیت در درس ریاضی عمومی یک شبه به دست نمیآید، برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید.
سری در ریاضیات عمومی
در ریاضیات یک سریِ متناظر با یک دنباله مانند {an}، از مجموع جزئی تمامی اعضای دنباله {an} به دست میآید.
سریها به این دو صورت است:
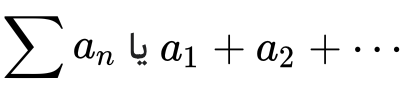
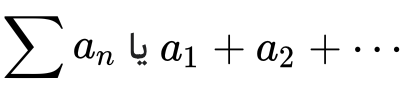
سریها انواع مختلفی مانند حسابی، هندسی، p سری، تلسکوپی و متناوب دارند.
واگرایی
اگر {an} دنبالهای از اعداد باشد و سری بهاین صورت باشد:
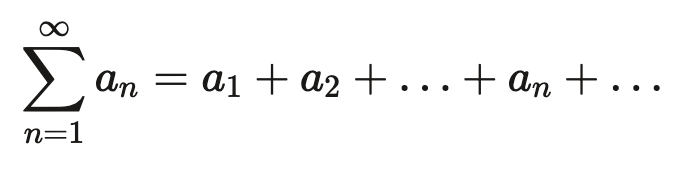
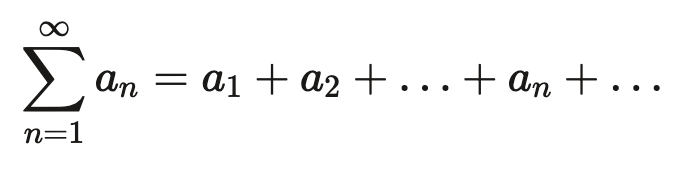
سری را واگرا میگوییم. درحقیقت، این سری در بینهایت به عددی نزدیک نمیشود. برای این دسته از سریها عدد مجموع مشخصی وجود ندارد.
همگرایی
در سری ها اگر سری در بینهایت به عدد ثابتی میل کند، سری را همگرا گویند که آن را بهاین صورت نشان میدهند:
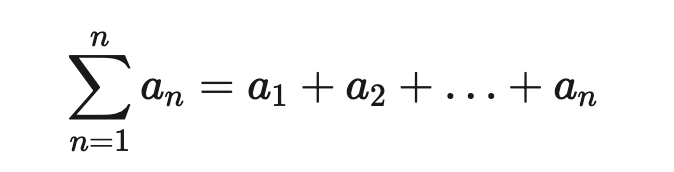
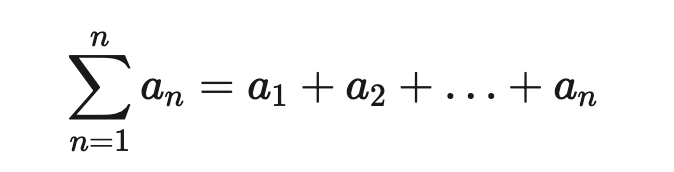
حاصل این عبارت را با Sn نشان میدهند. در حالتی که n→∞ برقرار باشد و Sn به L میل کند، در این صورت سری Sn را همگرا مینامند.
شرط لازم همگرایی
شرط لازم برای همگرایی سری صفرشدن حد جمله عمومی سری (an) در بینهایت است.


برای آشنایی با انتگرال ریاضی عمومی ۱ و ۲ این مطلب را مطالعه کنید:
کاربرد انتگرال در ریاضی عمومی ۱
آزمونهای همگرایی و واگرایی در سری ها
برای بررسی همگرایی و واگرایی سریها از برخی از آزمونهای همگرایی استفاده میکنیم. اگر شرط لازم همگرایی برقرار نباشد به سراغ این آزمون ها نرفته و سری را واگرا مینامیم.
آزمون مقایسه


آزمون نسبت حدی
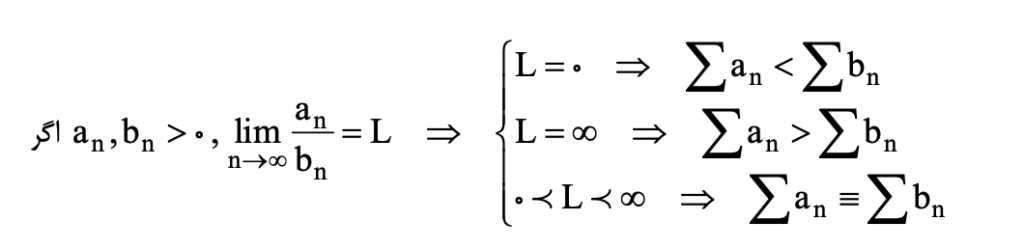
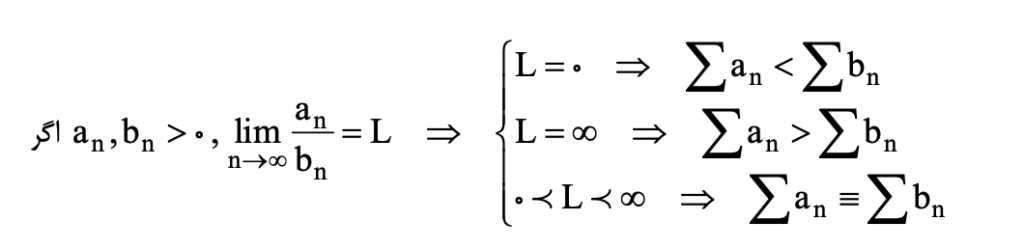
آزمون دالامبر


آزمون ریشه
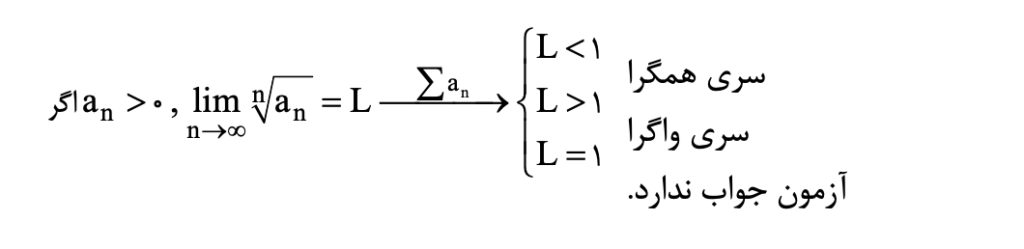
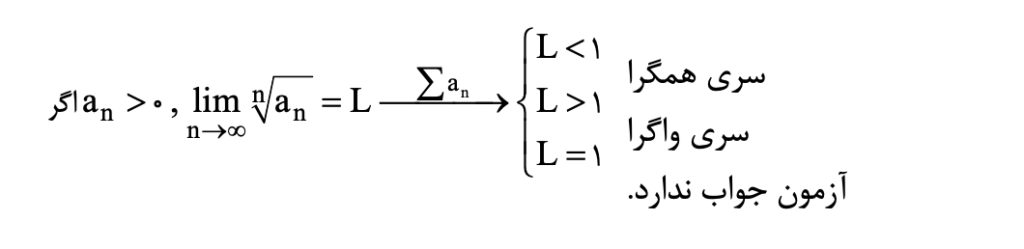
آزمون انتگرال


آزمون رابه


آزمون تراکم کوشی


آزمون آبل
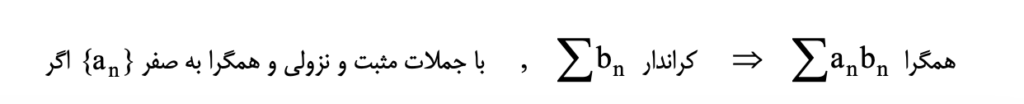
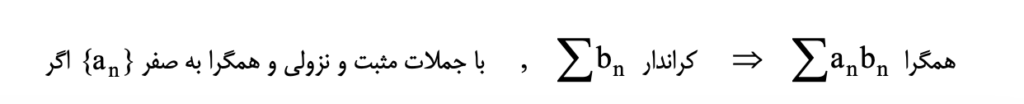
آزمون سریهای متناوب (لایپ نیتز)
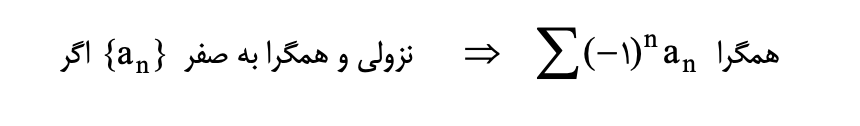
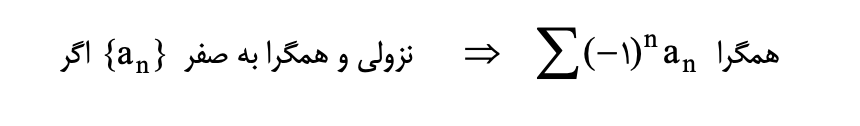
باتوجه به نوع سری با یک یا دو آزمون از آزمونهای بالا میتوانیم به همگرایی و واگرایی سری ها پی ببریم.
نکات همگرایی سریها


نمونه سوال




کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:


خوب است ولی تستها راندیدم
باسلام
ممنون از توجه شما
عالی
ممنون از توجه شما