کاربرد انتگرال در ریاضی عمومی ۱ چقدر است؟ در این مطلب بهصورت مفصل کاربردهای انتگرال را بررسی کردهایم. نکته مهم این است که موفقیت در درس ریاضی عمومی به تمرین زیاد نیاز دارد. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و تستهای زیادی حل کنید. در این متن کاربردهای انتگرال در ریاضی عمومی ۱ را بررسی میکنیم.
انتگرال
در ریاضیات انتگرال روشی است برای اختصاص اعداد به توابع، بهگونهای که جابهجایی مساحت، حجم و دیگر مفهومهای حاصل از ترکیب دادههای بینهایت کوچک را با آن بتوان توصیف کرد. انتگرالگیری یکی از دو عمل مهم در حساب دیفرانسیل و انتگرال است؛ عمل معکوس آن مشتقگیری است.
انتگرال و قواعد آن در ریاضیات چیست؟
کاربرد انتگرال
انتگرال در زندگی کاربردهای مختلفی دارد. در ادامه برخی از کاربردهای انتگرال در ریاضیات را بررسی میکنیم.
محاسبه مساحت محسور
از مهمترین کاربردهای انتگرال محاسبه مساحت میان دو تابع یا مساخت زیر نمودار یک تابع در بازه مشخص است. در محاسبه مساحت با انتگرالها باید توجه کنیم که هدف ما محاسبه مساخت است. پس قدرمطلق انتگرالهایی را که زیر محور xها قرار دارد در زمان محاسبه باید به دست آوریم.


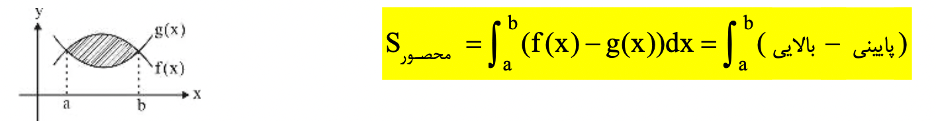
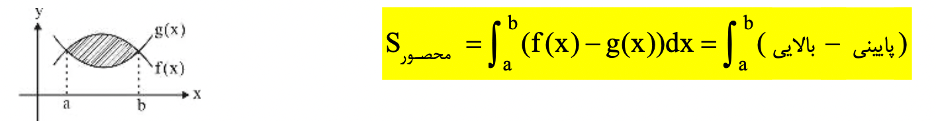
محاسبه حجم حاصل از دوران
یکی از کاربرد انتگرال ها محاسبه حجم است. از انتگرالها میتوان برای محاسبه حجم نمودارها و اجسامی که دوران میکنند استفاده کرد. با توجه به اینکه نمودار حول کدامیک از محورهای مختصات دوران میکند، روش محاسبه متفاوت خواهد بود. اگر نمودار حول محور xها دوران کند از روش دیسک استفاده میکنیم.


درصورتیکه سطح دوران یافته میان دو منحنی و در حالت کلی حول محور y=B دوران کند:
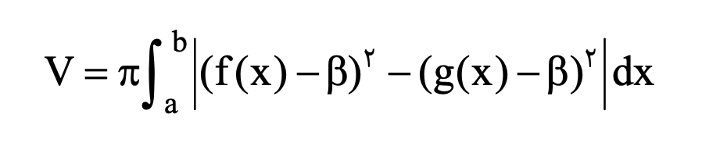
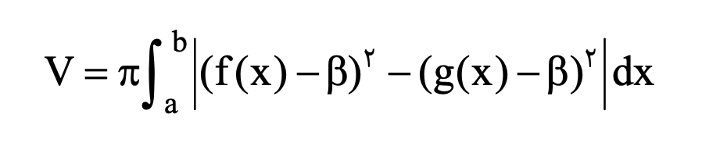
اگر دوران حول محور x=a باشد، از روش پوسته استوانه و این فرمول استفاده میکنیم:


اگر ناحیه با محور خود تقاطع نداشته باشد:


نمونه سوال




طول قوس
برای آنکه بتوانیم طول بخشی از یک نمودار را به دست آوریم نمیتوانیم از خطکش استفاده کنیم. یکی از موارد کاربرد انتگرال، محاسبه طول نموداردر بازه مشخص است. برای محاسبه طول قوس از این فرمول استفاده میکنیم:
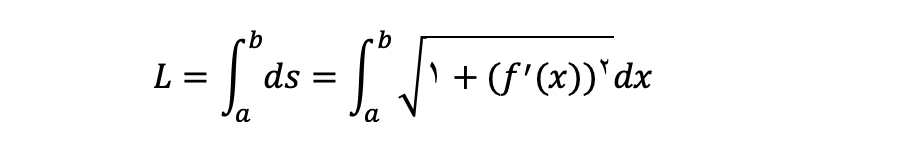
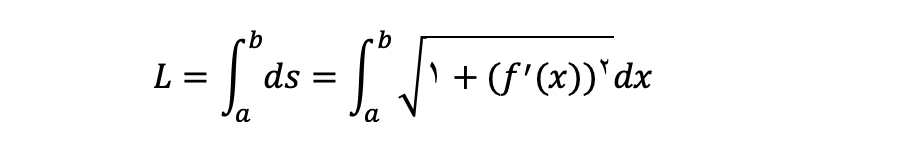
که به ds جز طول قوس میگویند.
سطح حاصل از دوران
از کاربردهای انتگرال محاسبه سطح حاصل از دوران است. درصورتیکه طول قوس را دوران دهیم، پوستهای حاصل میشود که مساحت آن از این رابطه به دست میآید:


اگر ناحیه با محور خود تقاطع نداشته باشد:


کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

