موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد. ضریب این درس در کنکور رشته مدیریت کسب و کار ۲ است و اهمیت آن بر داوطلبان پوشیده نیست. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید. مجانب و انواع آن از مباحث اصلی حد هستند که آن را معرفی خواهیم کرد.
اهمیت درس ریاضی عمومی ۱ و ۲
ریاضی عمومی ۱ و ۲ از دروس پایهای رشتههای مختلف است. اهمیت این درس به سه دلیل عمده بازمیگردد؛ اولین دلیل این است که این درس جزو سرفصلهای امتحانی بسیار مهم رشتههای مختلف است. دلیل دوم به محتوای ارائهشده در این درس بازمیگردد. محتوای این درس بهقدری مهم است که آشنایی با مفاهیم آن به درک مفاهیم سایر درسهای دورهی کارشناسی و سایر مواد آزمون کارشناسیارشد کمک شایانی میکند. سومین دلیل اهمیت این درس و کلاس آنلاین ریاضی عمومی ۱ و ۲ نوع نگاهی است که در حل مسائل این درس وجود دارد؛ این نگاه عاملی اساسی در شکلگیری تفکر انتقادی در حل مسائل است.
در این سری از مقالات برخی از موضوعات مهم دروس را با نگاه آموزشی و به صورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید.
مجانبها
مجانبها خطوطی هستند که رفتار تابع را در بی نهایت مشخص می کند.به طوری که درحالت حدی نمودار تابع و خط مجانب در بینهایت به هم نزدیک می شوند و نمودار تابع به هیچ عنوان در بی نهایت به این مجانب نمی رسد یعنی فقط به آن نزدیک می شود و فاصله نمودار تا خط آن، کم و کمتر می شود طوری که به صفر میل می کند. در هندسهٔ تحلیلی مُجانب یک منحنی، خطی است که فاصلهٔ منحنی از آن در بینهایت به صفر نزدیک میشود. در برخی حوزههای دیگر، مثلاً هندسهٔ جبری، مُجانب به صورت خطی تعریف میشود که در بینهایت بر منحنی مماس است.
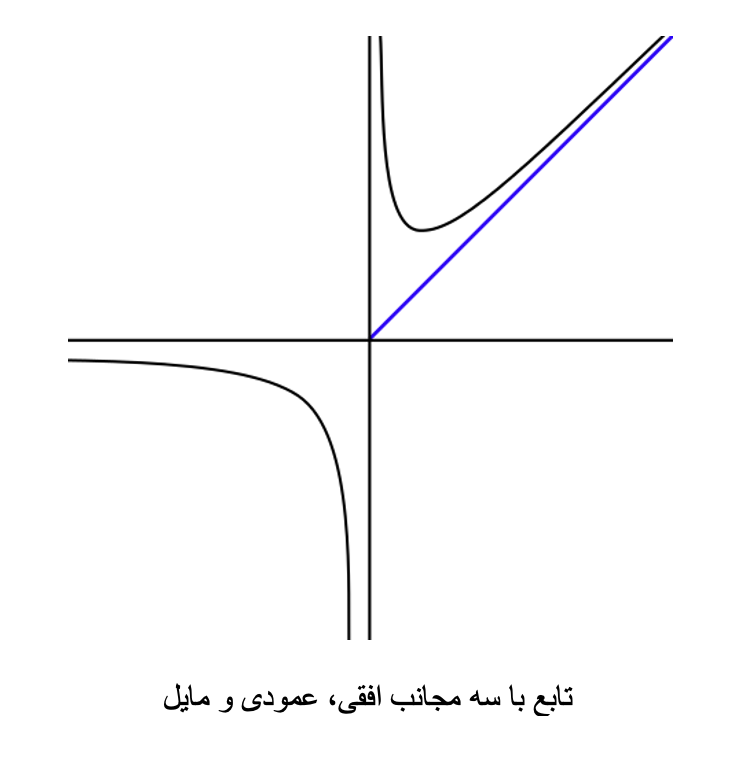

مجانبها سه نوع دارند: افقی، عمودی، و مایل. برای منحنیهای به شکل نمودار تابع y=f(x) ، مجانبهای افقی خطوطی هستند که نمودار تابع به هنگامی که x به +∞ یا −∞ میل میکند، به آن خطوط نزدیک میشود. مجانبهای عمودی خطوطی عمودی هستند که تابع در نزدیکی آنها بیکران افزایش یا کاهش مییابد. وهمچنین مجانبها به دو زاویه ای در هندسه گفته میشود که مجاور و مکمل یکدیگر باشند
مجانب قائم
مجانب قائم خطی است عمودی که در کنار منحنی حرکت می کند و در بی نهایت بر آن مماس می شود.یعنی خطی موازی محور Y هاست. در واقعاگر در تابعی به ازای x=a مقدارتابع یعنی y به سمت مثبت یا منفی بینهایت برود، آنگاه خط x=a مجانب قائم آن تابع می باشد. عموما توابع کسری و لگاریتمی دارای مجانب قائم هستند. شکل زیر نمونه ای از انواع مجانب قائم می باشد.


محاسبه
برای بدست آوردن مجانب قائم در توابع کسری به ترتیب زیر عمل میکنیم:
- ریشههای مخرج را بدست می آوریم.
- حد چپ و راست تابع را در هریک از ریشهها بدست میآوریم.
- هرکدام از ریشهها که در آن تابع به سمت بینهایت میل کند، آن ریشه مجانب قائم است.
- زمانی که ریشه مخرج ریشه صورت نیز باشد، باید حد تابع را برای بررسی شرایط بدست آورد.
مجانب افقی
زمانی تابع مجانب افقی دارد که مقدار تابع در =x ،به سمت یک عدد ثابت مثل y=a نزدیک می شود.در آن صورت می گوییم خـط y=a مجانب افقی تابع می باشد. توابعی که دامنه آنها محدود است، این نوع از مجانبها را ندارند زیرا مجانب افقی در ∞=x اتفاق می افتد. در توابع کسری اگر درجه صورت مساوی درجه مخرج یا بیشتر از درجه مخرج باشد، مجانب افقی داریم.که با استفاده از حد گیری در حالت اول y=aمجانب افقی خواهد بود (aیک عدد است) و در حالت دوم y=0مجانب افقی خواهد بود. شکل زیر نمونه ای از انواع مجانب افقی می باشد.
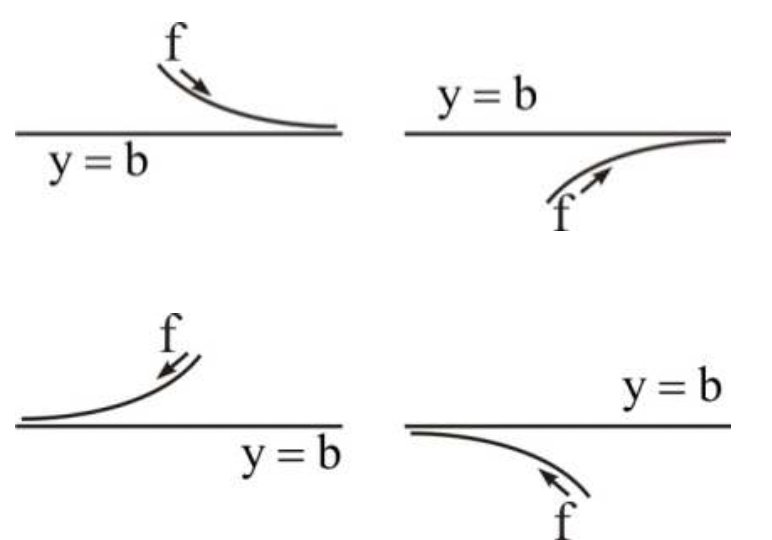

محاسبه
برای تعیین این دسته از مجانبها:
- باید دامنه تابع را مشخص کنیم.
- X را به سمت
و
سوق میدهیم تا در صورت موجود بودن مجانب افقی بدست میآید.
مجانب مایل
مجانب مایل خطی است که تحت آن اگر x به سمت بینهایت میل کند،y نیز در راستای آن به سمت بینهایت میل می کند. پس همx و هم y به سمت بی نهایت می روند.بنابر این اگر دامنه و یا برد تابعی محدود باشد، آن تابع مجانب مایل ندارد.
فرم کلی مجانبهای مایل به صورت خط y=ax+b می باشد.
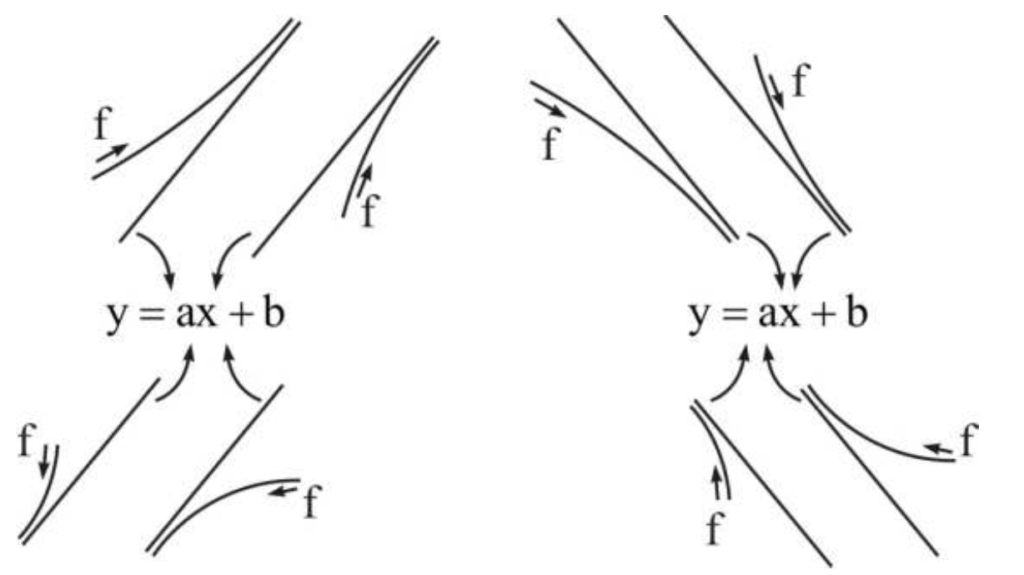

محاسبه
برای محاسبه مجانب مایل باید a و b را از روایط زیر بدست آوریم:
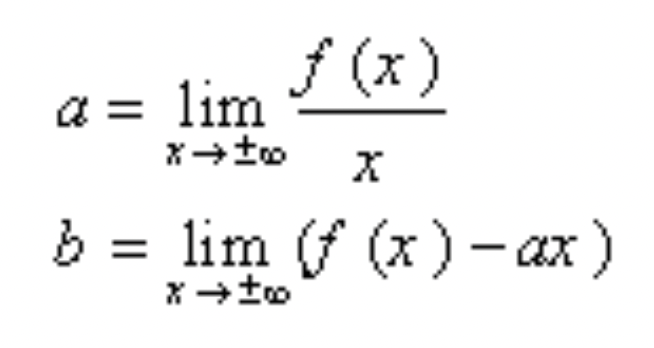
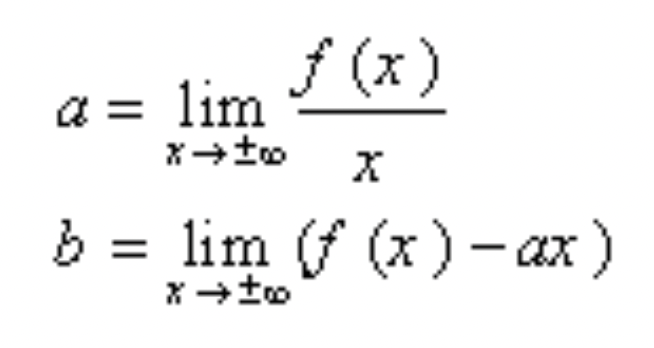
در توابع کسری که درجه صورت یک درجه از مخرج بیشتر باشد، مجانبهای مایل را با تقسیم صورت بر مخرج بدست آورد.
نمونه سوال
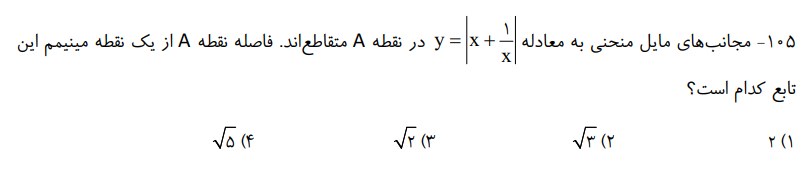
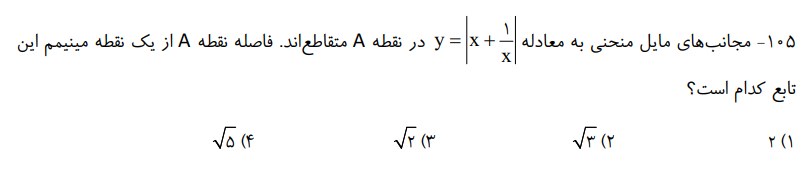
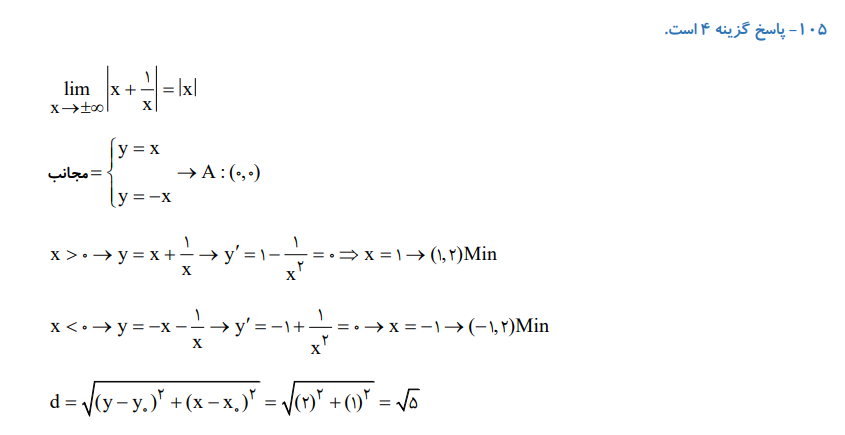
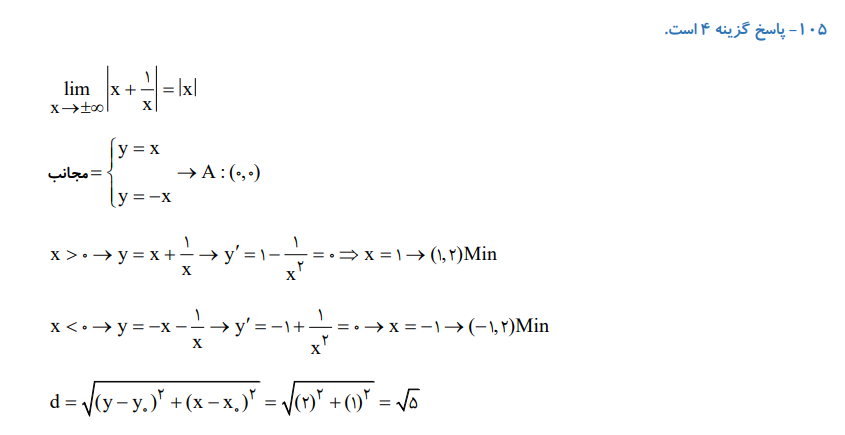
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:


به جز توابع کسری و لگاریتمی،دیگه چه توابعی میتونن مجانب قائم داشته باشن؟
باسلام
این توابع عموما مجانب قائم دارند اما توابعی مانند توابع پارامتری هم ممکن هست مجانب قائم داشته باشند