چقدر با حالات خاص هندسی در مختصات قطبی آشنا هستید؟ در این مطلب به این سرفصل از درس ریاضی عمومی ۱ و ۲ پرداختهایم. حالات خاص و مکان هندسی از موضوعهای جالب و پرکاربرد در ریاضیات است. تسلط به آن به شما کمک میکند بتوانید تستهای احتمالی آن در درس ریاضی عمومی ۱ و۲ کنکور کارشناسی ارشد را بهخوبی پاسخ دهید.
مختصات قطبی
همانطور که احتمالاً میدانید، در دستگاه مختصات کارتزینی فاصله افقی تا محور y را x و فاصله عمودی تا محور x را y مینامند. از طرفی میتوان نقطه را بهشکلی متفاوت نیز نشان داد. در این روش مختصات نقطه را با استفاده از دو پارامتر نشان میدهند. این دو پارامتر فاصله از مرکز مختصات و زاویه با محور افقی هستند.
در ریاضیات دستگاه مختصات قطبی (بهانگلیسی: Polar coordinate system) یک دستگاه مختصات دوبعدی است که در آن هر نقطه از یک صفحه با یک فاصله از یک نقطه مرجع و یک زاویه از یک جهت مرجع تعیین میشود. نقطه مرجع (معادل با مبدأ در دستگاه مختصات دکارتی) قطب نامیده میشود و پرتوی عبوری از قطب در جهت مرجع، محور قطبی شناخته میشود.
معرفی کلاس آنلاین ریاضی عمومی ۱ و ۲
حالات خاص هندسی در مختصات قطبی
اگر r=f(teta) را تابعی در مختصات قطبی در نظر بگیریم، مکانهای هندسی خاص زیر را در این فضا خواهیم داشت:
دایره به مرکز مبدا
اگر در مختصات قطبی با معادله به شکل زیر روبهرو شویم، یک دایره خواهیم داشت:


این دایره به مرکز مبدآ خواهد بود و شعاعی بهاندازه r0 خواهد داشت.
نیمخط
مکان هندسی دوم معادله بهاین شکل:
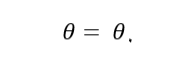
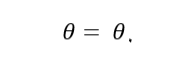
است. این مکان هندسی نیمخطی خواهد بود که از مبدآ مختصات عبور میکند و زاویه آن با جهت مثبت محور ox زاویه را خواهد ساخت. به این نیمخط شعاع گویند.
خط
در مکانهای هندسی اگر معادله زیر را داشته باشیم
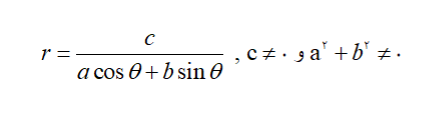
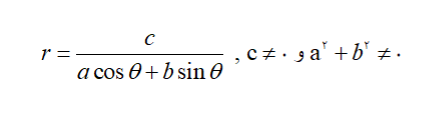
درحقیقت، معادله خط به فرم


خواهد بود.
منحنیها
از حالات خاص قطبی، منحنیها هستند که با دو معادله مشخص خواهند شد.
معادله اول به صورت:


است. برای این حالت این سه فرض را خواهیم داشت:
- اگر ab<0 باشد، منحنی هذلولی؛
- اگر ab>0 باشد، منحنی بیضی و در حالت خاصتر اگر a و b نیز با یکدیگر برابر باشند، دایره؛
- اگر ab=0 دو خط موازی.
معادله دوم منحنیهای خاص این شکل را خواهد داشت:
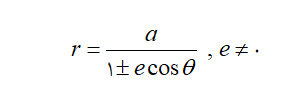
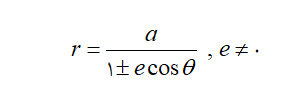
در این معادله نیز مفروضات خواهیم داشت:
- اگر e>1 هذلولی با خروج از مرکز e را خواهیم داشت؛
- اگر e<1 بیضی با خروج از مرکز e را خواهیم داشت؛
- اگر e=1 سهمی را خواهیم داشت.
مکان هندسی های قطبی
در مختصات قطبی مکان هندسی قطبی تنوع زیادی دارند. در این جدول این حالتهای خاص بههمراه فرم معادله و شکلشان آورده شدهاند. از این شکلها برای محاسبه راحتتر در مختصات قطبی میتوان استفاده کرد:
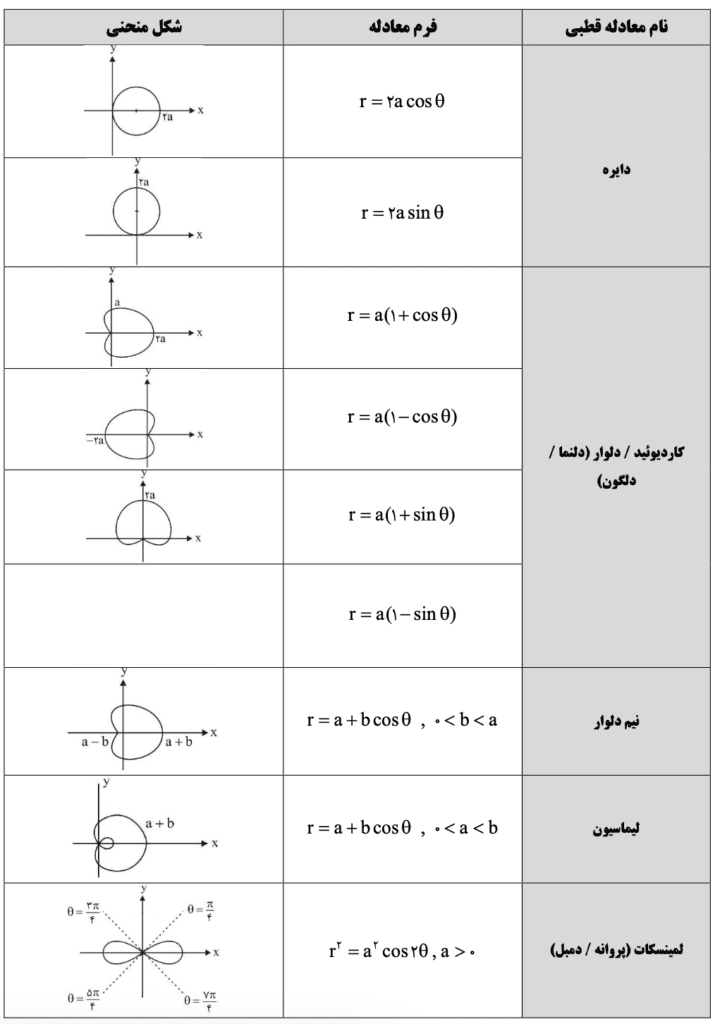

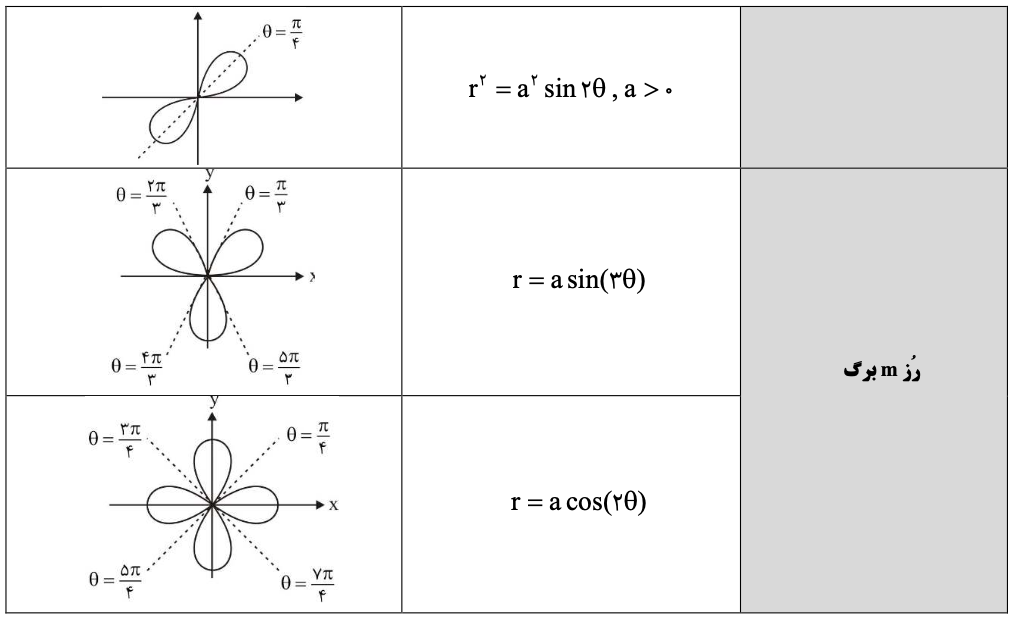

کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

