تابع هزینه یا Loss Function چیست؟ راهنمای جامع استفاده از توابع هزینه در ماشین لرنینگ

آیا تابه‌حال فکر کرده‌اید که چطور الگوریتم‌های یادگیری ماشین تصمیم می‌گیرند یک مدل خوب است یا بد؟ یکی از کلیدهای این فرایند تابع هزینه (Loss Function) است. این تابع به ما کمک می‌کند تا اختلاف میان مقدارهای پیش‌بینی‌شده و مقدارهای واقعی را اندازه‌گیری کنیم و درنتیجه، مدل‌های بهتری بسازیم. بدون داشتن یک معیار مشخص برای سنجش عملکرد مدل، بهینه‌سازی و بهبود یک مدل ماشین لرنینگ تقریباً غیرممکن است.

 اهمیت تابع هزینه

تابع هزینه‌ها نقشی اساسی در آموزش مدل‌های یادگیری ماشین دارند. بدون یک معیار مشخص برای اندازه‌گیری خطا، بهبود و تنظیم مدل‌ها تقریباً غیرممکن است. این توابع به ما نشان می‌دهند که مدل ما چقدر از هدف خود دور است و چه مقدار بهینه‌سازی نیاز دارد؛ به‌عبارت دیگر، تابع هزینه به عنوان یک راهنما عمل می‌کند که مسیر صحیح بهینه‌سازی را به ما نشان می‌دهد. هر چه مقدار این تابع کمتر باشد، نشان‌دهنده دقت بالاتر مدل است و درنتیجه، مدل بهتری داریم.

تعریف تابع هزینه

تابع هزینه یا تابع خطا معیاری است که میزان خطای مدل را نشان می‌دهد. این تابع اختلاف میان خروجی پیش‌بینی‌شده مدل و خروجی واقعی را محاسبه می‌کند و به ما کمک می‌کند تا مدل را بهبود دهیم؛ به‌عبارت دیگر، تابع هزینه تفاوت میان واقعیت و پیش‌بینی مدل را به‌صورت عددی نشان می‌دهد. هر چه مقدار این تابع کمتر باشد، نشان‌دهنده دقت بالاتر مدل است و مدل بهتری داریم. این توابع در فرایند آموزش مدل‌ها نقش کلیدی ایفا می‌کنند؛ زیرا بهینه‌سازی مدل بر اساس کاهش مقدار این توابع انجام می‌شود.

 انواع تابع هزینه

تابع هزینه‌های مختلفی برای کاربردهای متفاوت وجود دارند. هر کدام از این توابع مزایا و معایب خاص خود را دارند و انتخاب مناسب آنها بستگی به نوع مسئله و داده‌های موجود دارد. به طور کلی، انتخاب تابع هزینه مناسب می‌تواند تاثیر زیادی بر عملکرد نهایی مدل داشته باشد. در اینجا به بررسی برخی از انواع رایج تابع هزینه می‌پردازیم.

میانگین مربعات خطا

میانگین مربعات خطا یا Mean squared error (MSE) یکی از رایج‌ترین توابع هزینه است که میانگین مربع خطاهای پیش‌بینی را محاسبه می‌کند. این تابع به خاطر حساسیت به خطاهای بزرگ مورد توجه قرار گرفته است. MSE برای مسائل رگرسیون بسیار مناسب است و کمک می‌کند تا مدل‌هایی با دقت بالا ساخته شوند. با این حال، حساسیت بالای آن به خطاهای بزرگ ممکن است در برخی موارد باعث کاهش دقت مدل شود. فرمول محاسبه این تابع به‌صورت زیر است:

که در آن، n تعداد ‌داده‌ها است، y_i مقدار واقعی خروجی و ŷ_i مقدار پیش‌بینی‌شده آن است. همان‌طور که مشخص است، میانگین‌گیری از مربع اختلاف‌ها، بر روی همه نقاط داده‌ها انجام می‌شود.

لازم است بدانید که مقیاس MSE مربع واحد اصلی مقادیر برچسب (Label) است. مثلا اگر مقادیر برچسب‌ها بر حسب دلار باشند، MSE بر حسب دلار به توان دو خواهد بود. این ویژگی باعث می‌شود که MSE به خطاهای بزرگ حساس‌تر باشد، زیرا مربع خطاها را در محاسبات خود لحاظ می‌کند.

پیاده‌سازی در پایتون

برای پیاده‌سازی تابع هزینه MSE در پایتون ابتدا داده‌های نمونه‌ای را تعریف و سپس تابعی برای محاسبه خطای میانگین مربعات ایجاد می‌کنیم؛ سپس برای وزن‌های مختلف، میانگین مقادیر خطا، به‌کمک تابع تعریف‌شده محاسبه می‌شوند:

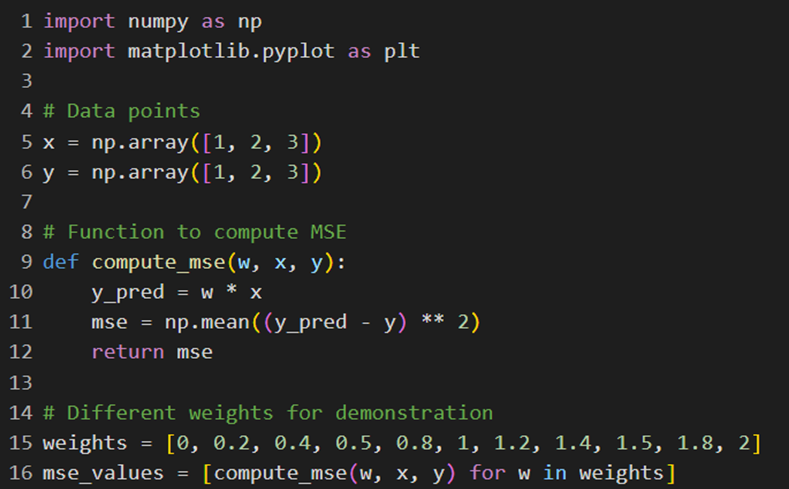
 در ادامه با این کد دو نمودار ترسیم می‌کنیم:

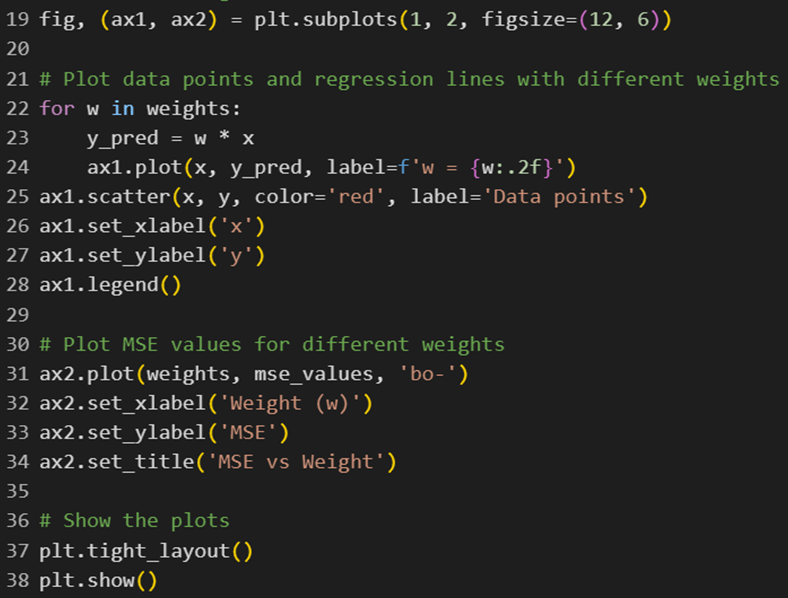
خروجی این کد در این شکل آمده است:

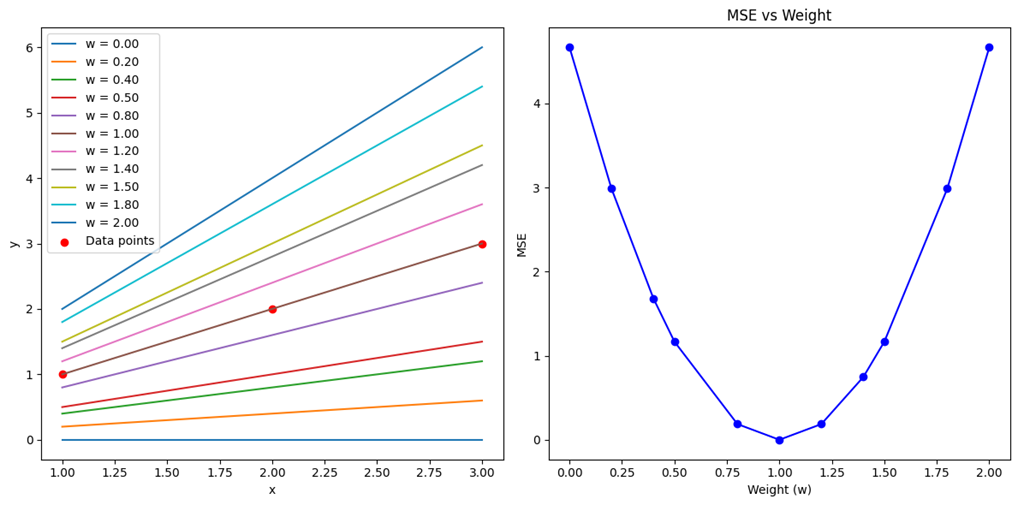
در این شکل نمودار سمت چپ نشان‌دهنده خطوط رگرسیون برای وزن‌های مختلف است و نمودار سمت راست مقدار MSE را دربرابر وزن‌ها نشان می‌دهد. این به ما کمک می‌کند تا بفهمیم چگونه تغییر وزن‌ها بر دقت مدل تأثیر می‌گذارد.

استفاده از MSE در کتابخانه‌های معروف

اغلب کتابخانه‌های معروف مربوط به ماشین لرنینگ این تابع هزینه را به‌صورت ازپیش‌ساخته‌شده در خود تعریف کرده‌اند. در ادامه نحوه استفاده از این تابع هزینه را در هر یک از این کتابخانه‌ها و فریم‌ورک‌ها می‌بینید:

Sklearn

Keras

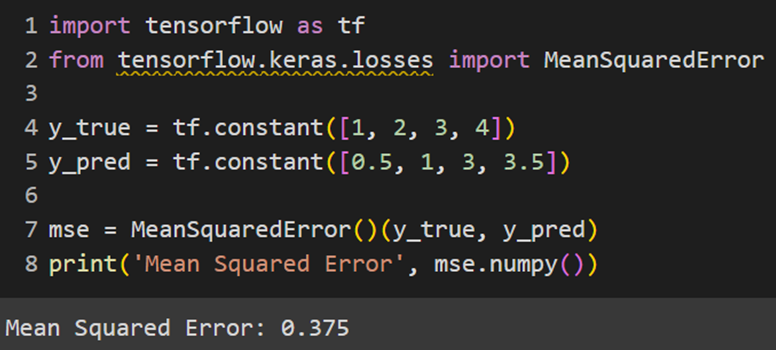
PyTorch

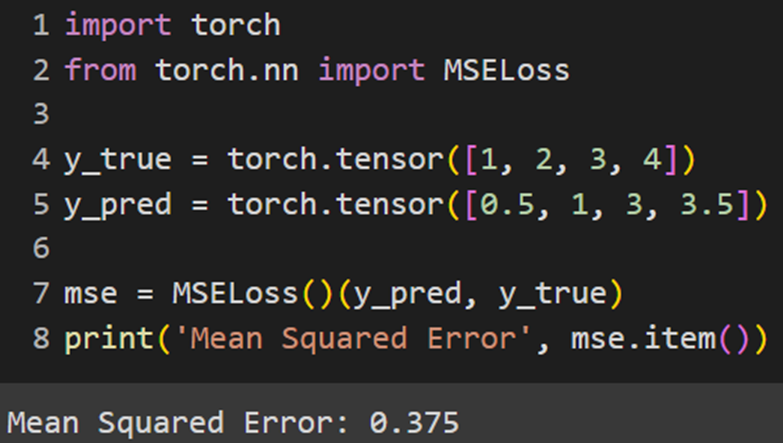
Jax

کتابخانه Jax تابع هزینه MSE را به‌صورت ازپیش‌تعیین‌شده ندارد؛ بنابراین در صورت کار با این فریم‌ورک باید این تابع را خودمان به‌این صورت تعریف کنیم:

MXNet

فرمولی که تابع L2Loss به‌عنوان تابع هزینه MSE از آن استفاده می‌کند، کمی با فرمولی که دیگر کتابخانه‌ها از آن استفاده می‌کنند متفاوت است؛ درواقع همان فرمول ارائه‌شده در قسمت توضیحات است که تقسیم بر دو شده است؛ به‌‌همین دلیل، برای مشاهده پاسخ مشابه با قسمت‌های قبل حاصل را دوبرابر می‌کنیم:

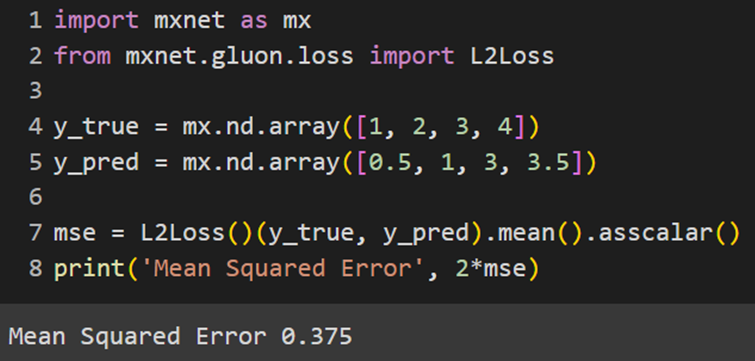
میانگین مطلق خطا

Mean absolute error (MAE) میانگین قدر مطلق خطاهای پیش‌بینی را برای مسئله‌های رگرسیون اندازه‌گیری می‌کند. این تابع در مقایسه با MSE کمتر به خطاهای بزرگ حساس است و معمولاً برای مدل‌هایی که به مقاومت دربرابر نویز نیاز دارند استفاده می‌شود. MAE، به‌دلیل سادگی و کارایی بالا، در بسیاری از مسئله‌ها کاربرد دارد و به‌خصوص در مواقعی که داده‌ها نویز دارند مفید است. فرمول محاسبه این تابع به‌این صورت است:

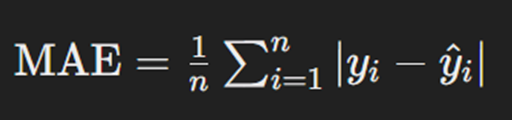
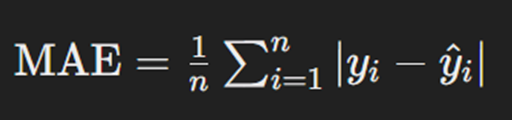
که در آن n تعداد ‌داده‌هاست، y_i مقدار واقعی خروجی و ŷ_i مقدار پیش‌بینی‌شده آن برای داده iام است. همان‌طور که از فرمول مشخص است، میانگین‌گیری از قدر مطلق اختلاف‌ها روی همه نقاط داده‌ها انجام می‌شود.

لازم است بدانید مقیاس MAE همان واحد اصلی مقدارها برچسب (Label) است؛ به‌عبارت دیگر، اگر مقدارهای برچسب‌ها مثلاً برحسب دلار باشند، MAE نیز برحسب دلار خواهد بود. این ویژگی به این می‌انجامد که تفسیر MAE ساده‌تر و مستقیماً قابل‌فهم باشد.

پیاده‌سازی در پایتون

پیاده‌سازی این تابع هزینه مشابه MSE است، با این تفاوت که این بار از فرمول MAE برای محاسبه میزان خطا استفاده می‌کنیم. در اینجا نیز مقدارهای خطا برای وزن‌های مختلف محاسبه می‌شوند:

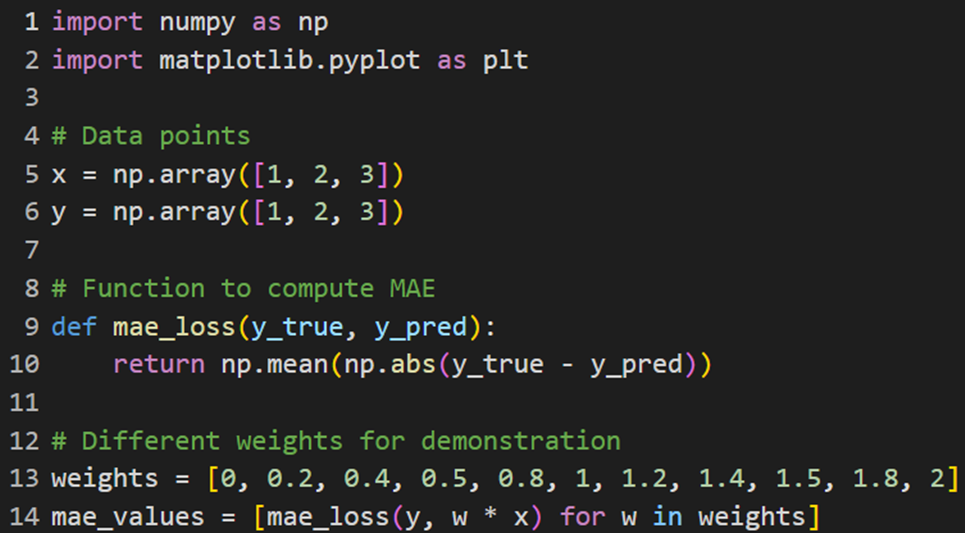
سپس نمودارهای مشابهی برای نمایش خطوط رگرسیون و مقدارهای خطا ترسیم می‌شوند:

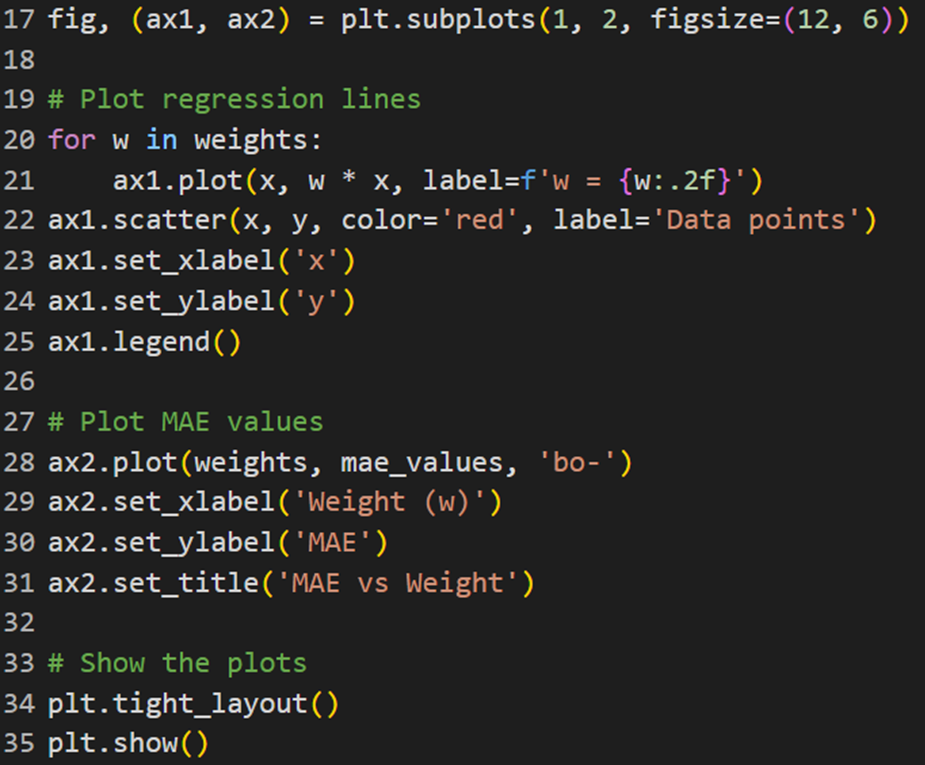
خروجی کد بالا در این شکل آمده است:

استفاده از MAE در کتابخانه‌های معروف

بیشتر کتابخانه‌های معروف پایتونی مربوط به ماشین لرنینگ این تابع هزینه را به‌صورت ازپیش‌ساخته‌شده در خود تعریف کرده‌اند. نحوه استفاده از این تابع هزینه را در هر یک از این کتابخانه‌ها و فریم‌ورک‌ها می‌بینید:

Sklearn

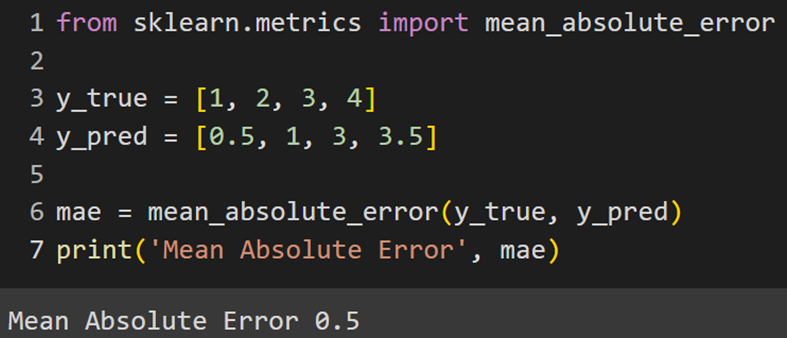
Keras

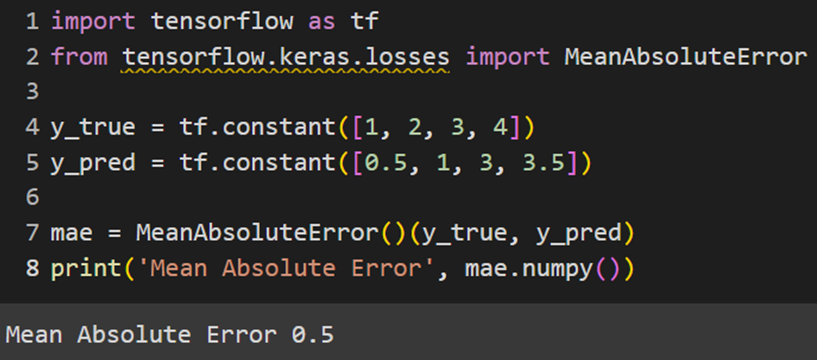
PyTorch

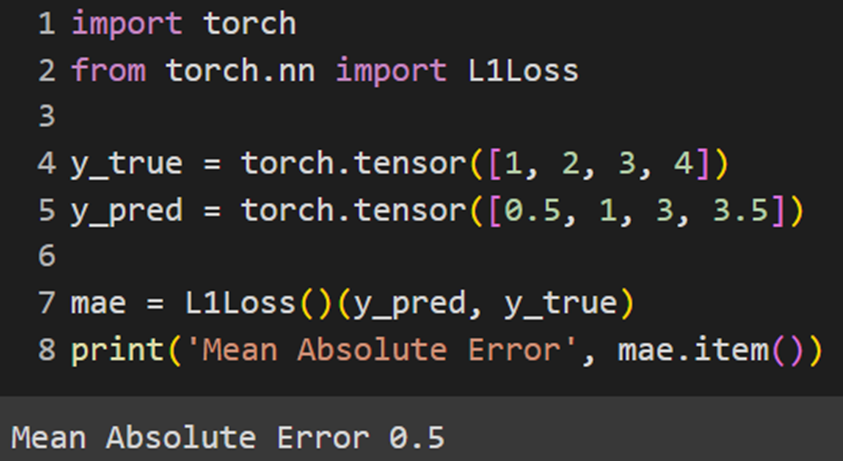
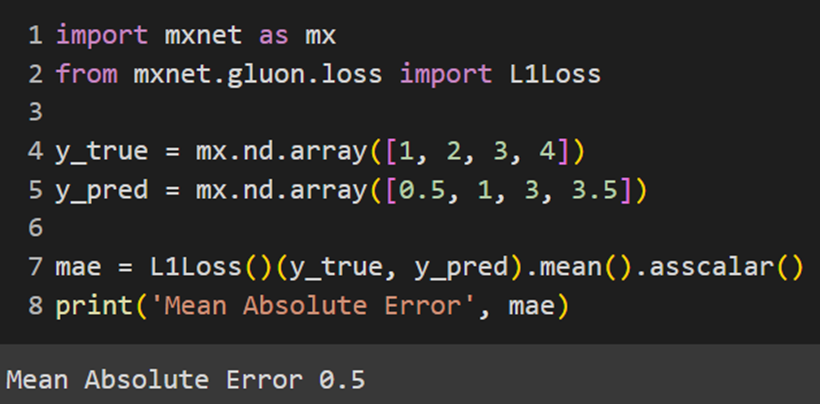
Jax

کتابخانه Jax، تابع هزینه MAE را به‌صورت ازپیش‌تعیین‌شده ندارد؛ بنابراین درصورتی‌که با این فریم‌ورک کار می‌کنیم، باید این تابع را خودمان به‌این صورت تعریف کنیم:

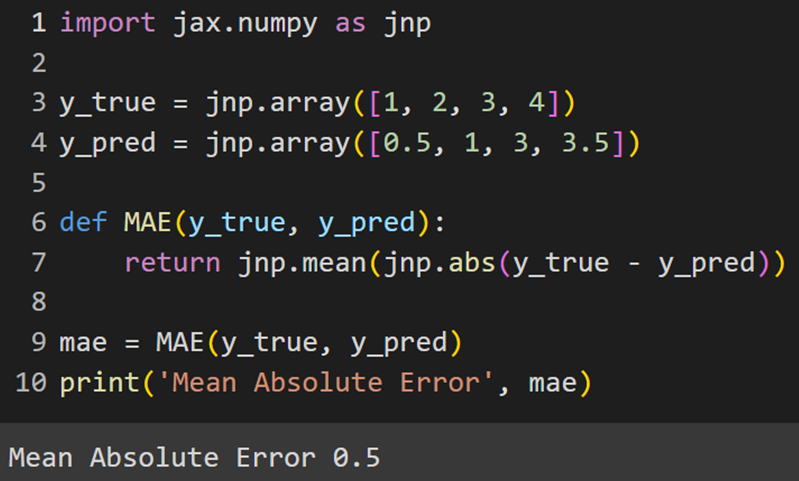
MXNet

تابع هزینه هوبر

Huber Loss ترکیبی از MSE و MAE است. این تابع در صورت کوچک‌بودن خطاها مانند MSE رفتار می‌کند و در صورت بزرگ‌بودن خطاها مانند MAE عمل می‌کند؛ به‌عبارت دیگر، Huber Loss از مزیت‌های هر دو تابع MSE و MAE بهره می‌برد و درعین‌حال معایب آن‌ها را کاهش می‌دهد. این تابع برای مسئله‌های رگرسیون که در آن‌ها خطاهای بزرگ نادر ولی مهم هستند بسیار مناسب است. فرمول محاسبه این تابع به‌این صورت است:

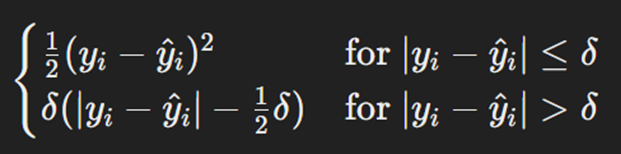
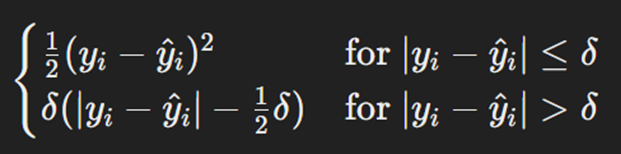
که در آن y_i مقدار واقعی خروجی و ŷ_i مقدار پیش‌بینی‌شده آن است. دلتا (δ) نیز پارامتر آستانه (Threshold) نام دارد.

پیاده‌سازی در پایتون

در این قسمت برای محاسبه خطا از فرمول تابع Huber Loss استفاده و مقدارهای خطا را برای وزن‌های مختلف محاسبه می‌کنیم:

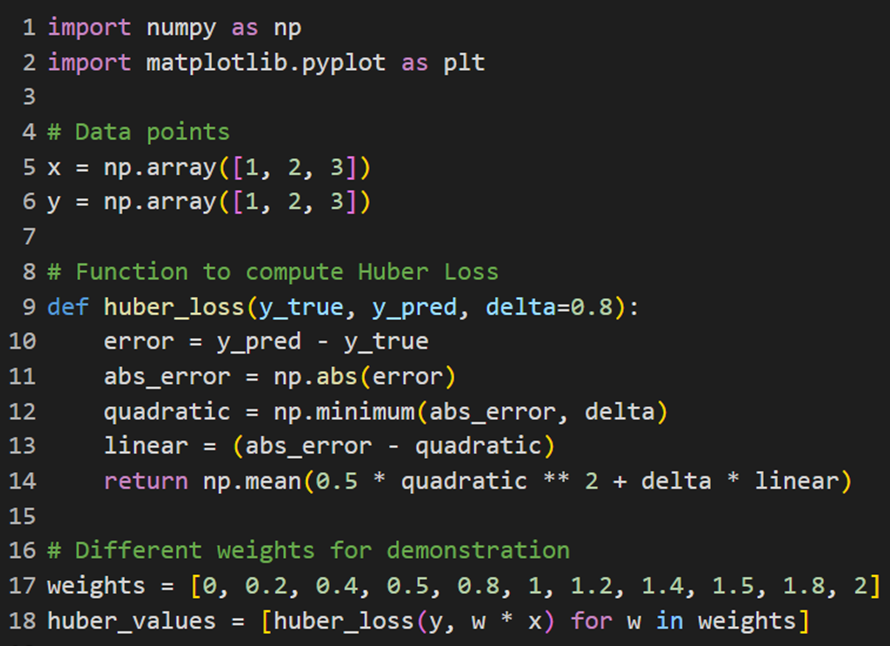
سپس از کدی که در توابع هزینه قبلی استفاده کردیم برای ترسیم نمودارهای مربوط استفاده می‌کنیم:

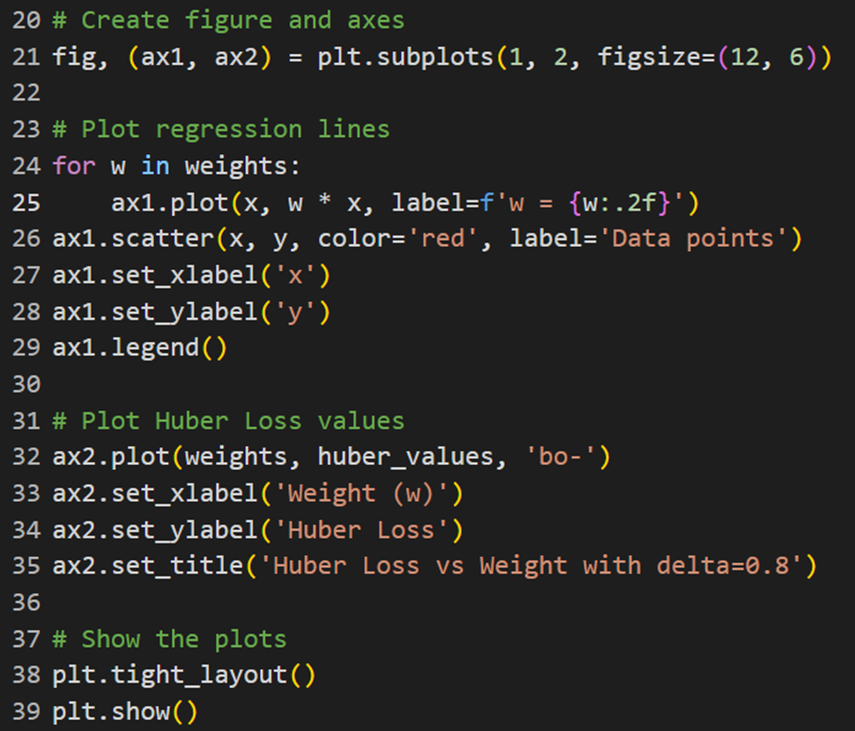
خروجی این کد در این شکل آمده است که نشان می‌دهد چگونه مقدارهای خطا با تغییر وزن‌ها تغییر می‌کنند:

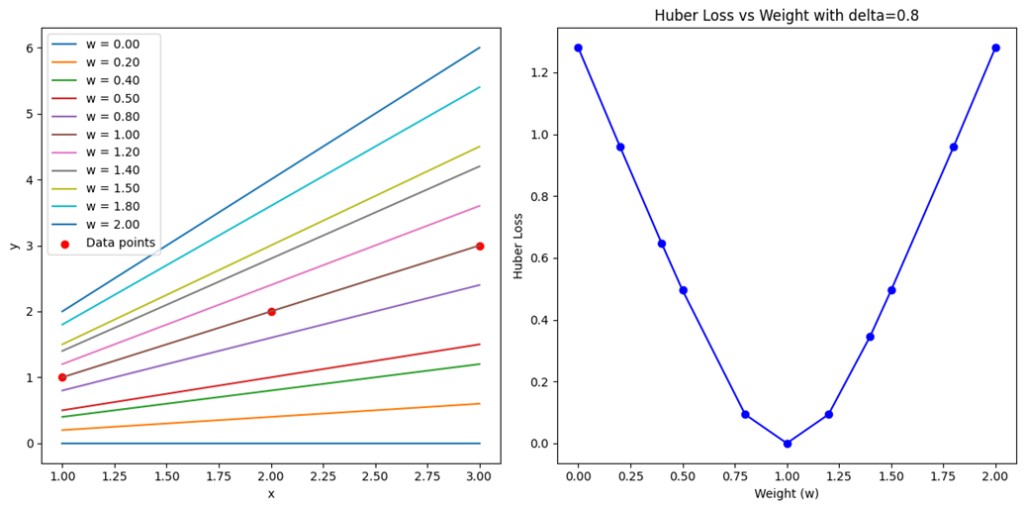
استفاده از Huber Loss در کتابخانه‌های معروف

برخی کتابخانه‌های معروف پایتونی مربوط به ماشین لرنینگ، این تابع هزینه را به‌صورت ازپیش‌ساخته‌شده در خود تعریف کرده‌اند. نحوه استفاده از این تابع هزینه را در هر یک از این کتابخانه‌ها و فریم‌ورک‌ها می‌بینید:

Sklearn

سایکیدلرن این تابع را به‌صورت آماده ندارد، اما در صورت نیاز می‌توانیم بااستفاده از این کد این تابع را به‌صورت دستی پیاده‌سازی کنیم:

Keras

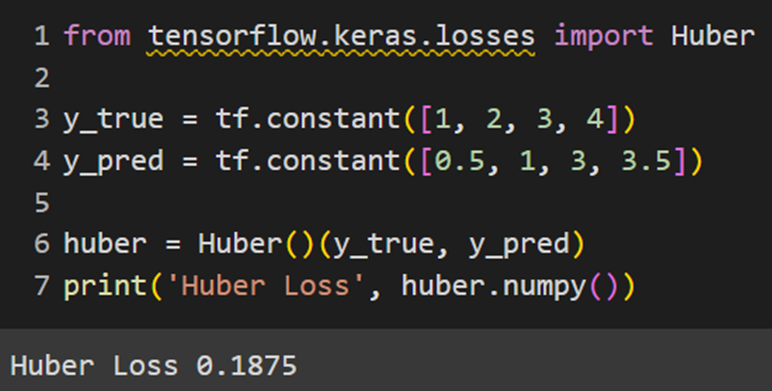
PyTorch

Jax

کتابخانه Jax تابع هزینه Huber Loss را به‌صورت ازپیش‌تعیین‌شده ندارد؛ بنابراین در صورت کار به این فریم‌ورک، باید این تابع را خودمان به‌این صورت تعریف کنیم:

MXNet

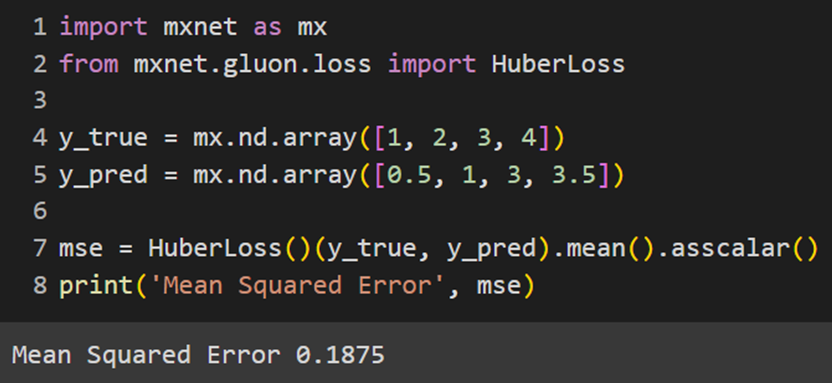
تابع هزینه ریشه میانگین مربعات خطا

RMSE یا Root Mean Squared Error یک معیار رایج برای ارزیابی دقت مدل‌های رگرسیون است. RMSE با محاسبه جذر میانگین مربع خطاها، میزان انحراف پیش‌بینی‌ها از مقدارهای واقعی را اندازه‌گیری می‌کند. این تابع، به‌دلیل حساسیت به خطاهای بزرگ، می‌تواند نشان‌دهنده دقت کلی مدل باشد. RMSE به‌ویژه در مسائلی که خطاهای بزرگ تاثیر زیادی می‌گذارند مفید است؛ برای مثال، در پیش‌بینی قیمت مسکن یا پیش‌بینی میزان فروش محصولات، RMSE می‌تواند معیار مناسبی برای ارزیابی مدل باشد. فرمول محاسبه این تابع به‌این شکل است:

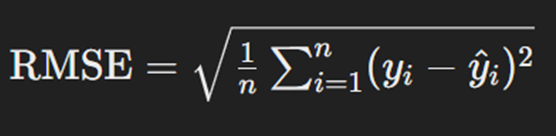
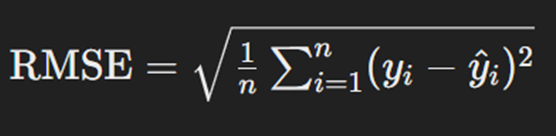
که در آن n تعداد ‌داده‌هاست، y_i مقدار واقعی خروجی و ŷ_i مقدار پیش‌بینی‌شده آن برای داده iام است. همان‌طور که از فرمول مشخص است، پیش از جذرگرفتن، میانگین‌گیری از مربع اختلاف‌ها، روی همه نقاط داده‌ها انجام می‌شود.

لازم به ذکر است که مقیاس RMSE مانند MAE همان واحد اصلی مقدارهای برچسب (Label) است؛ به‌عبارت دیگر، مثلاً اگر مقدارهای برچسب‌ها برحسب دلار باشند، RMSE نیز برحسب دلار خواهد بود. RMSE دلیل حساسیت به خطاهای بزرگ و بازگرداندن مقیاس به واحد اصلی، اغلب به‌عنوان معیاری جامع‌تر برای ارزیابی مدل‌ها در نظر گرفته می‌شود.

پیاده‌سازی در پایتون

برای پیاده‌سازی تابع هزینه RMSE نیز از این کد برای محاسبه خطای جذر میانگین مربعات استفاده می‌کنیم:

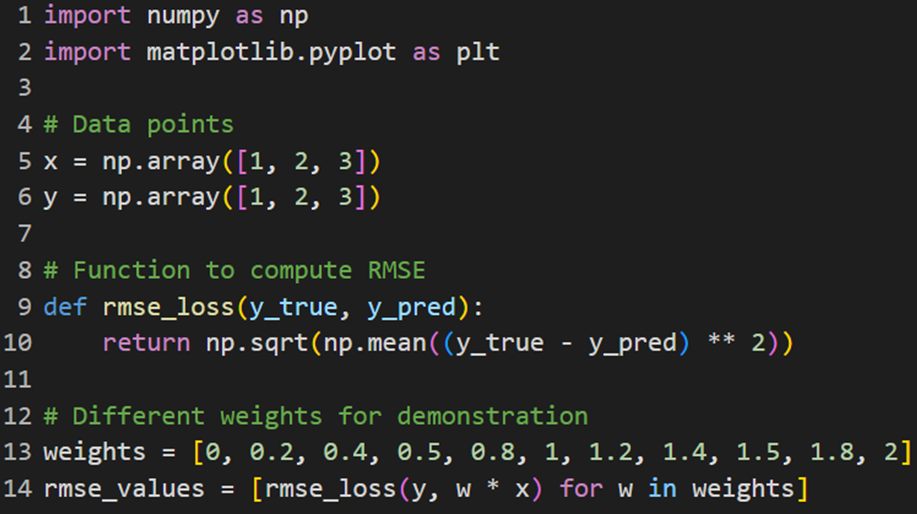
RMSE به‌نوعی مشابه MSE است، اما تفسیر آن به‌دلیل داشتن همان واحدها به مقادیر واقعی ساده‌تر است.

برای ترسیم نمودارهای این تابع هزینه نیز می‌توان مشابه توابع قبل از این کد استفاده کرد:

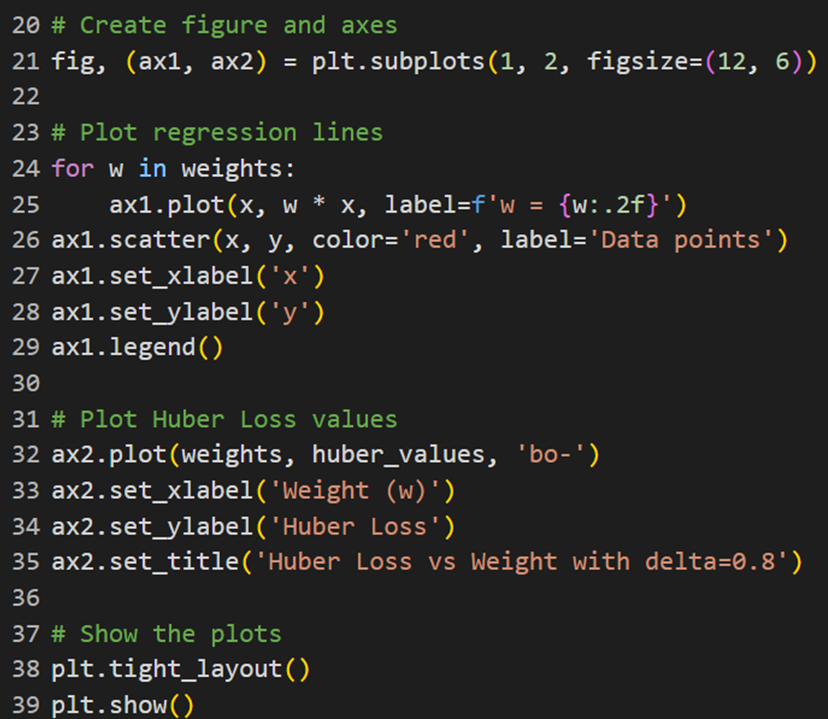
نمودارهای ترسیم‌شده به‌کمک کد بالا در‌ این شکل قابل‌مشاهده است و نشان می‌دهند چگونه مقدارهای خطا با تغییر وزن‌ها تغییر می‌کنند:

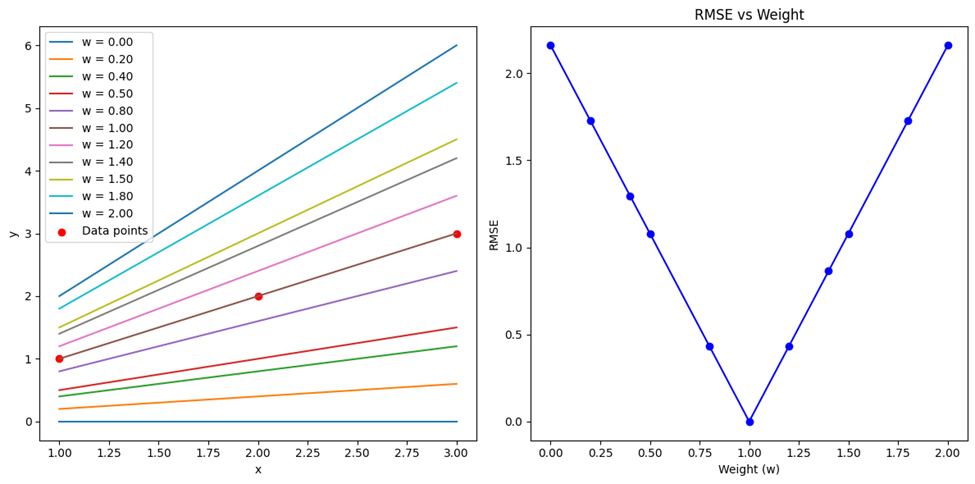
استفاده از RMSE در کتابخانه‌های معروف

برخی کتابخانه‌های معروف پایتونی مربوط به ماشین لرنینگ این تابع هزینه را به‌صورت ازپیش‌ساخته‌شده در خود تعریف کرده‌اند. نحوه استفاده از این تابع هزینه را در هر یک از این کتابخانه‌ها و فریم‌ورک‌ها می‌بینید:

Sklearn

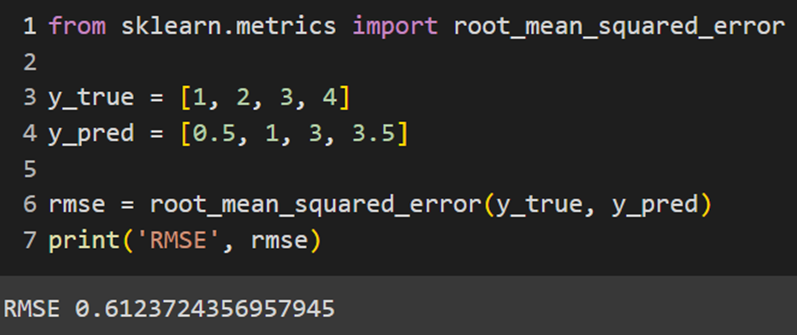
Keras

کراس ازجمله فریم‌ورک‌هایی است که این تابع را به‌صورت ازپیش‌ساخته‌شده ندارد و باید خودمان آن را به‌این صورت پیاده‌سازی کنیم:

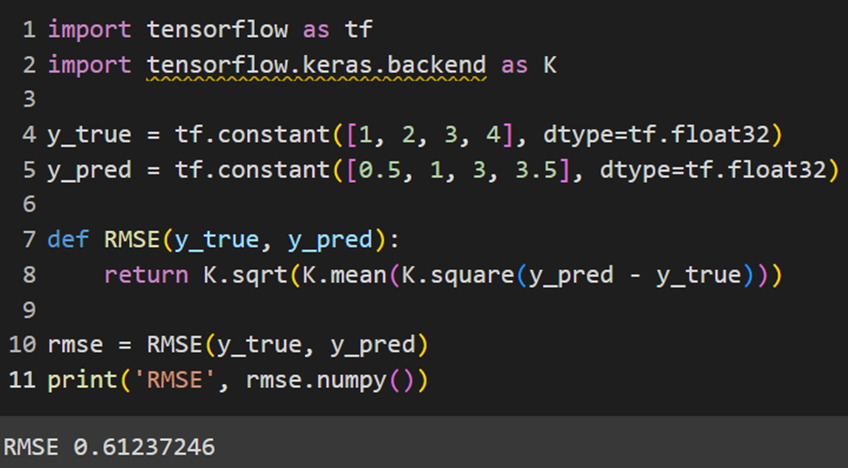
PyTorch

در پایتورچ نیز لازم است خودمان این تابع را بسازیم و از آن استفاده کنیم:

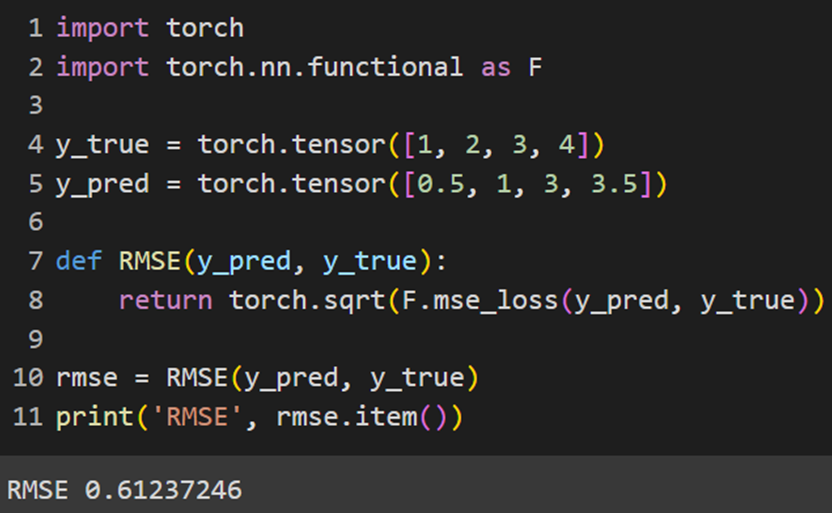
Jax

مانند کراس و پایتورچ، Jax نیز این تابع هزینه را به‌طور آماده ندارد و لازم است خودمان آن را بسازیم:

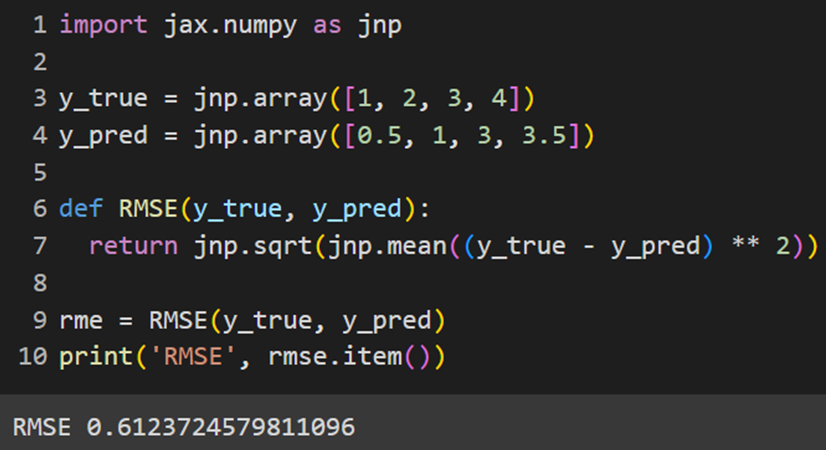
MXNet

مانند سه پکیج قبلی، MXNet نیز این تابع را ندارد و باید به‌صورت دستی آن را تعریف کنیم:

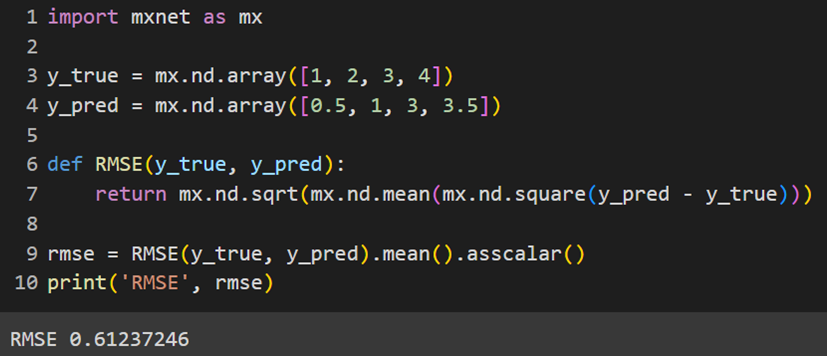
تابع هزینه مربع لگاریتمی

MSLE یا Mean Squared Logarithmic Error تابع زیان دیگری است که در مسئله‌های رگرسیون کاربرد دارد. این تابع برای مسائلی مناسب است که در آن‌ها مقدارهای پیش‌بینی‌شده و مقدارهای واقعی تفاوت‌های بزرگی دارند. MSLE، به‌جای محاسبه تفاوت‌های مستقیم، تفاوت‌های لگاریتمی مقدارها را محاسبه می‌کند که به این می‌انجامد تأثیر مقدارهای بسیار بزرگ یا کوچک کاهش یابد. این تابع به‌ویژه در مسائلی که داده‌ها به‌طور نمایی افزایش می‌یابند مفید است. فرمول محاسبه این تابع به‌این شکل است:

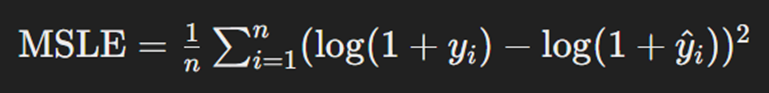
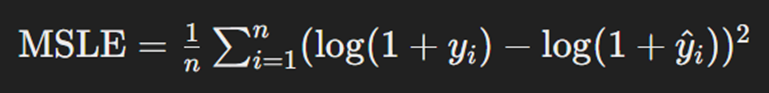
که در آن n تعداد ‌داده‌ها است، y_i مقدار واقعی خروجی و ŷ_i مقدار پیش‌بینی‌شده آن برای داده iام است. همان‌طور که از فرمول مشخص است، میانگین‌گیری از مجذور اختلاف لگاریتم‌ها، روی همه نقاط داده‌ها انجام می‌شود. این لگاریتم‌گیری برای مدیریت مقدارهایی است که ممکن است بسیار کوچک یا بسیار بزرگ باشند؛ همچنین جمع‌کردن مقدارهای پیش‌بینی‌شده و واقعی با عدد یک، از صفرشدن عبارت جلوی تابع لگاریتم که عدد منفی بی‌نهایت را به‌عنوان خروجی برمی‌گرداند جلوگیری می‌کند.

پیاده‌سازی در پایتون

در این کد از تابع خطای میانگین لگاریتم مربعات (MSLE) برای محاسبه میزان خطا استفاده و میزان خطا را برای هر وزن محاسبه می‌کنیم:

سپس از کد زیر برای ترسیم نمودارهای خطوط رگرسیون برای وزن‌های مختلف و مقدار MSLE در مقابل وزن‌ها استفاده می‌کنیم:

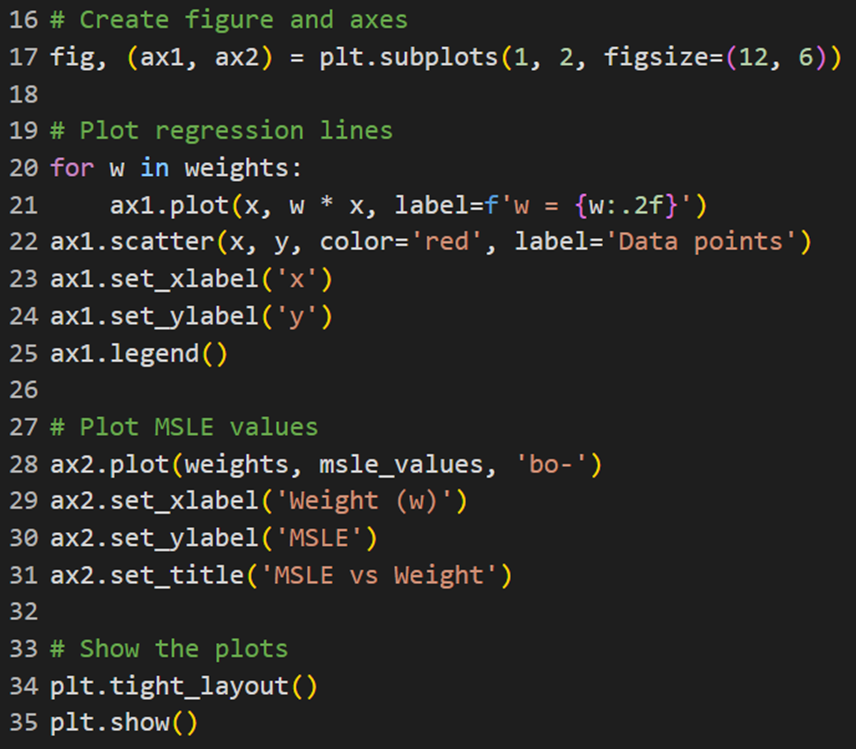
نمودارهای ترسیم‌شده در این شکل نشان می‌دهند که چگونه مقادیر خطا با تغییر وزن‌ها تغییر می‌کنند:

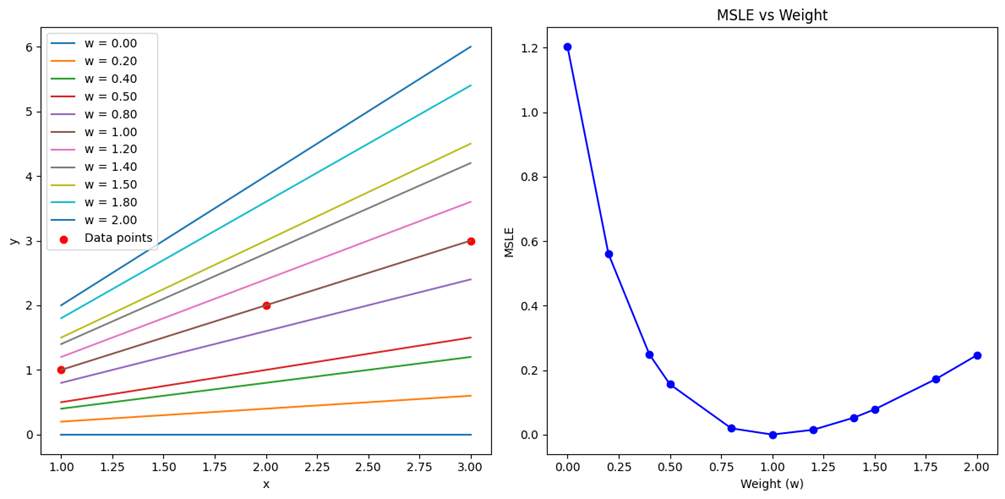
استفاده از MSLE در کتابخانه‌های معروف

برخی از فریم‌ورک‌های ماشین لرنینگ پایتون این تابع خطا را به‌صورت ازپیش‌ساخته‌شده در خود تعبیه کرده‌اند. در ادامه نحوه استفاده از این تابع هزینه را در هر یک از کتابخانه‌ها آموزش می‌دهیم:

Sklearn

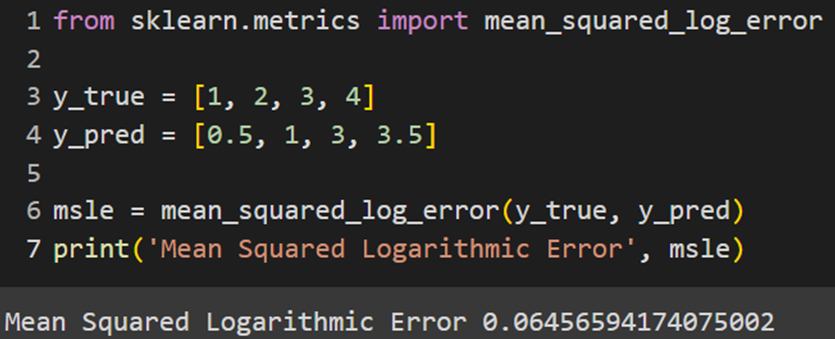
Keras

PyTorch

پکیج پایتورچ این تابع هزینه را به‌طور پیش‌فرض در خود تعبیه نکرده است؛ بنابراین برای استفاده از این تابع، باید به‌صورت دستی آن را تعریف کنیم:

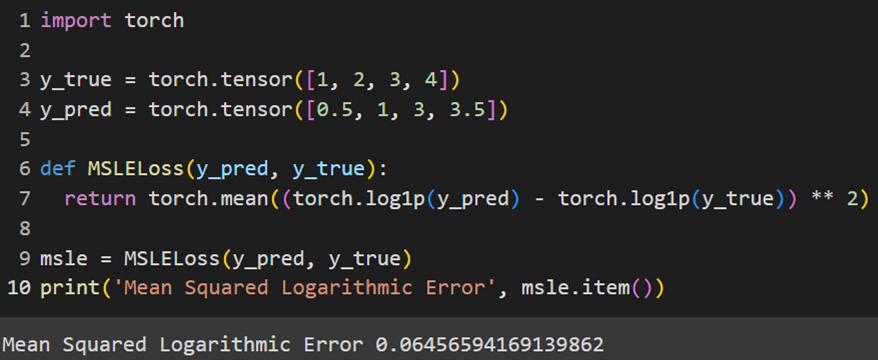
Jax

مانند پایتورچ، Jax نیز این تابع هزینه را ندارد:

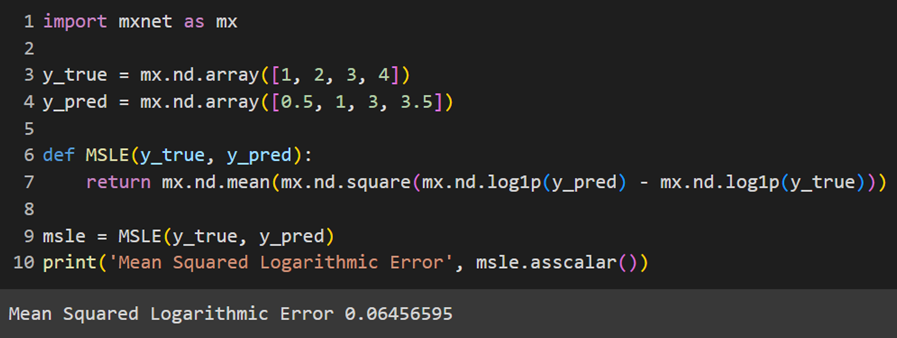
MXNet

این پکیج نیز تابع هزینه مربع لگاریتمی را به‌صورت ازپیش‌ساخته‌شده ندارد و باید آن را خودمان تعریف کنیم:

تابع هزینه لگاریتم کسینوس هیپربولیک

Log-Cosh Loss یکی دیگر از توابعی است که ویژگی‌های خوب MSE و MAE را ترکیب می‌کند. این تابع به‌سرعت تغییرات خطاهای بزرگ را کنترل می‌کند و پایداری بیشتر مدل را رقم می‌زند. Log-Cosh Loss، به‌خصوص در مواقعی که داده‌ها دارای نویز زیادی هستند، عملکرد خوبی دارد و می‌تواند دقت مدل رگرسیون را بهبود بخشد. فرمول محاسبه این تابع هزینه به‌این شکل است:

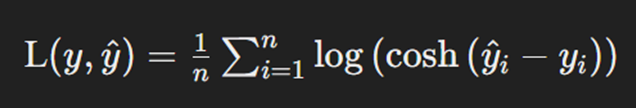
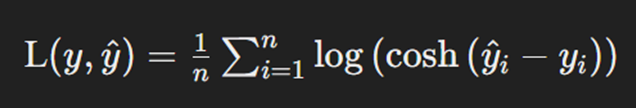
در این فرمول n تعداد ‌داده‌هاست، yi مقدار واقعی خروجی و ŷ_i مقدار پیش‌بینی‌شده آن برای داده iام است. فرمول محاسبه کسینوس هیپربولیک که پیش از لگاریتم‌گیری روی تفاضل مقدار واقعی و پیش‌بینی‌شده اعمال می‌شود به‌این صورت است:

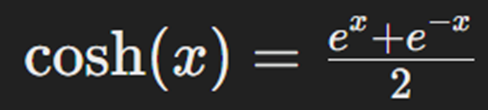
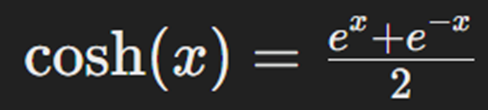
لگاریتم و کسینوس هیپربولیک به کنترل تأثیر خطاهای بزرگ کمک می‌کنند؛ زیرا رشد آن‌ها آهسته‌تر از یک تابع درجه دوم است.

پیاده‌سازی در پایتون

برای پیاده‌سازی این تابع هزینه از کد زیر برای محاسبه خطای لگاریتم کسینوس هیپربولیک (Log-Cosh Loss) استفاده و میزان خطا را برای هر وزن محاسبه می‌کنیم:

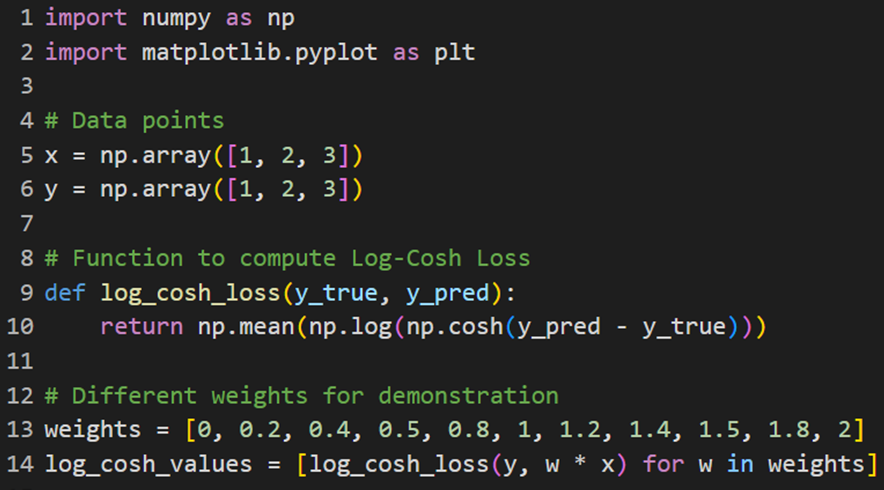
برای رسم نمودارهای مربوط نیز این کد را اجرا می‌کنیم:

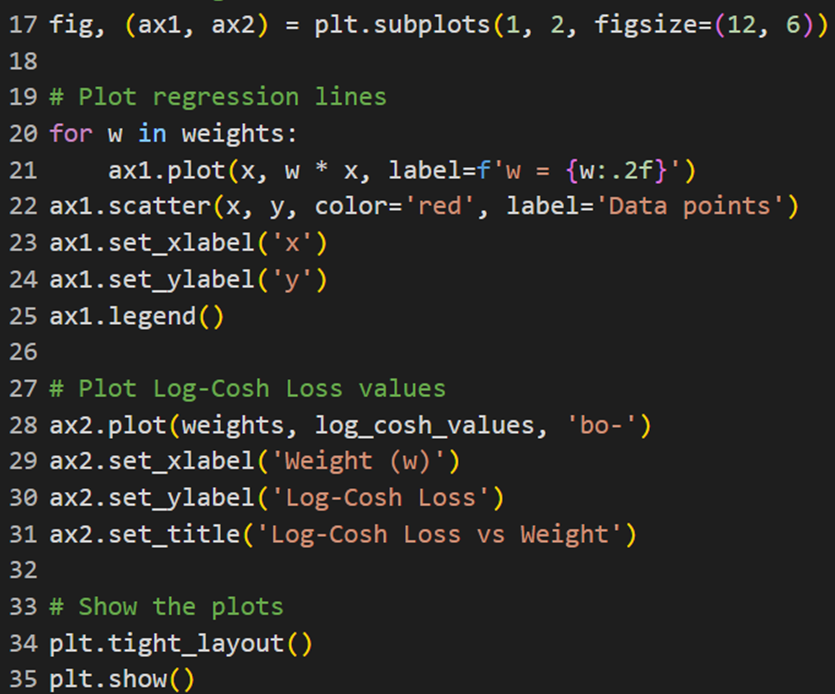
خروجی این کد نیز به‌این شکل درمی‌آید:

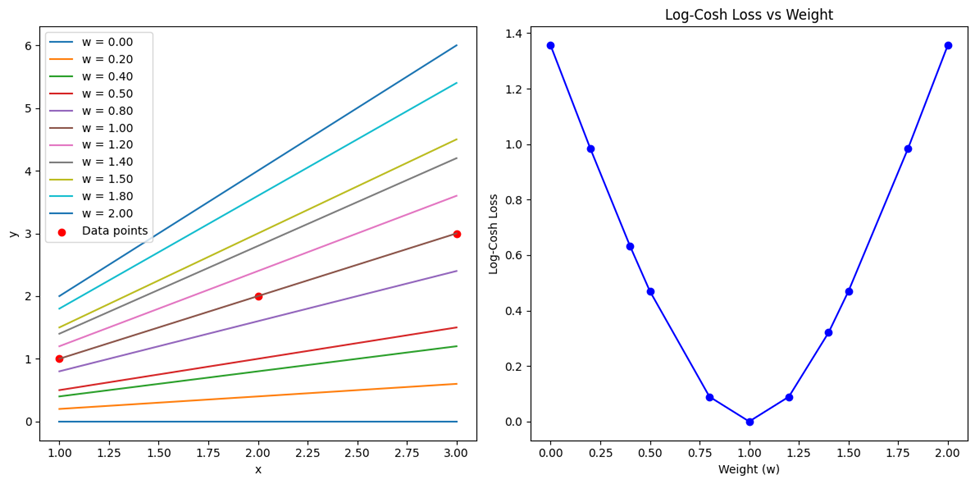
استفاده از Log-Cosh Loss در کتابخانه‌های معروف

برای استفاده از این تابع هزینه در بیشتر کتابخانه‌های معروف ماشین لرنینگ باید آن را تعریف کنیم؛ در واقع به‌جز فریم‌ورک کراس، هیچ کتابخانه‌ دیگری آن را به‌صورت ازپیش‌ساخته‌شده ندارد.

Sklearn

سایکیدلرن این تابع را به‌صورت آماده ندارد، اما درصورت نیاز می‌توانیم بااستفاده از این کد این تابع را به‌صورت دستی پیاده‌سازی کنیم:

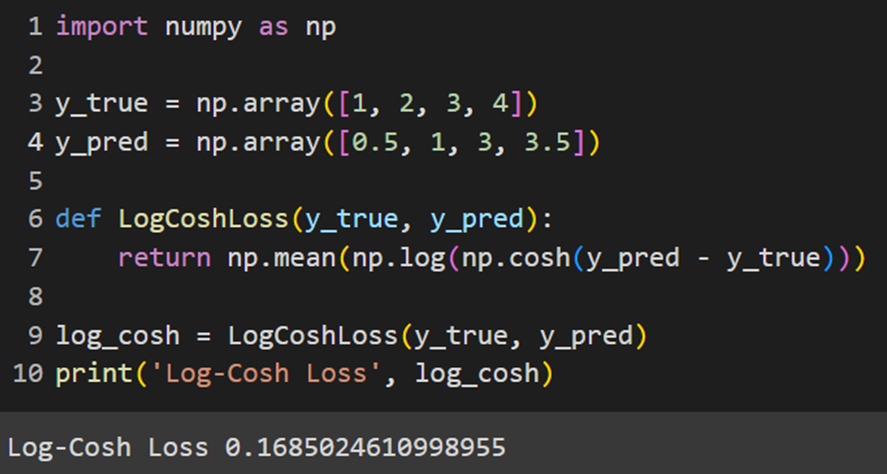
Keras

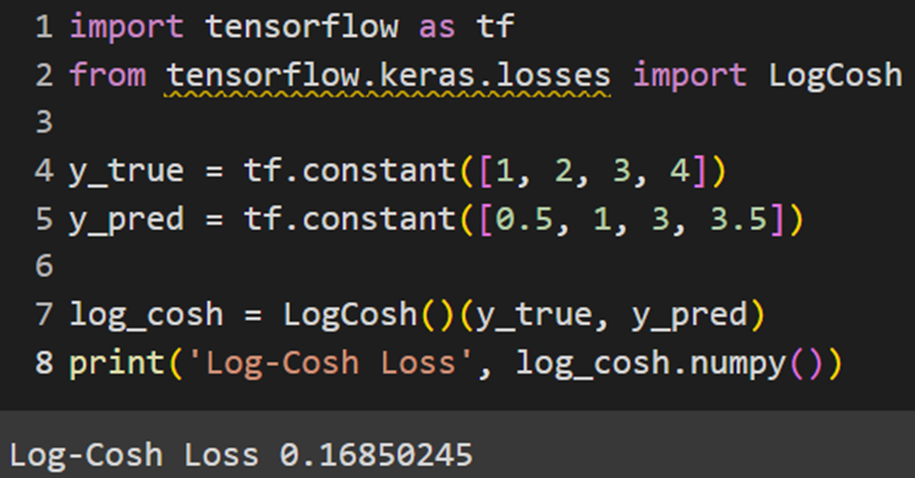
PyTorch

برای استفاده از این تابع هزینه در پایتورچ لازم است خودمان آن را تعریف کنیم:

Jax

در Jax نیز باید خودمان تابع هزینه لگاریتم کوسینوس هیپربولیک را تعریف کنیم:

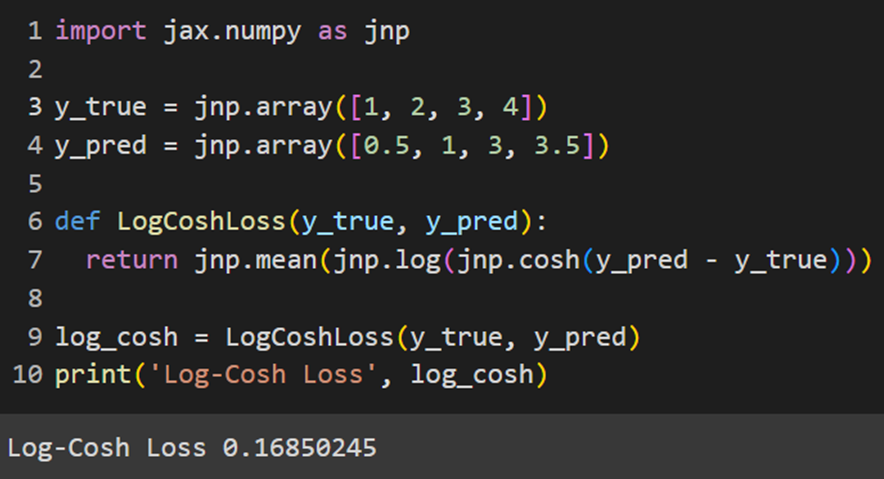
MXNet

در این پکیج نیز تابع مدنظر به‌صورت پیش‌فرض تعریف نشده است:

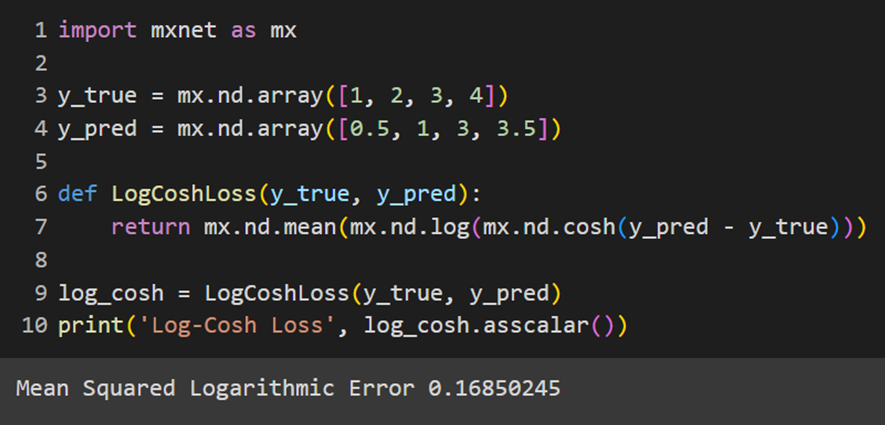
تابع هزینه کاتربار

تابع هزینه کاتربار یا Quantile Loss برای مسائل رگرسیون استفاده می‌شود. این تابع به مدل‌ها کمک می‌کند تا مقادیر مختلفی از توزیع داده‌ها را پیش‌بینی کنند، به‌جای تمرکز بر میانگین. تابع هزینه کاتربار به مدل اجازه می‌دهد تا به‌جای تمرکز بر میانگین داده‌ها، بتواند پیش‌بینی‌هایی برای بخش‌های خاصی از توزیع داده‌ها انجام دهد؛ برای مثال، در یک مجموعه داده‌ای که توزیع گسترده‌ای دارد مدل می‌تواند با استفاده از Quantile Loss مقادیر واقع در پایین‌ترین دهک (یعنی ۱۰ درصد پایینی) یا بالاترین دهک (یعنی ۱۰ درصد بالایی) را به‌خوبی پیش‌بینی کند.

این ویژگی به‌ویژه زمانی مفید است که پیش‌بینی دقیق در این نقاط توزیع داده‌ها اهمیت دارد؛ مثلاً در پیش‌بینی نوسانات بازار یا تشخیص ریسک‌های بالا در بیمه اهمیت پیدا می‌کند. این تابع به مدل‌ها امکان می‌دهد تا پیش‌بینی‌های دقیق‌تری در شرایط مختلف ارائه کنند. فرمول این تابع به‌این صورت است:

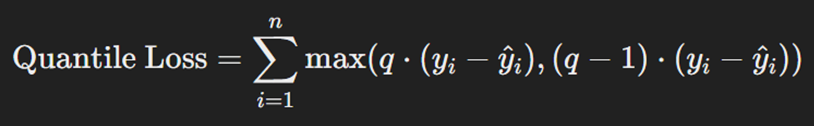
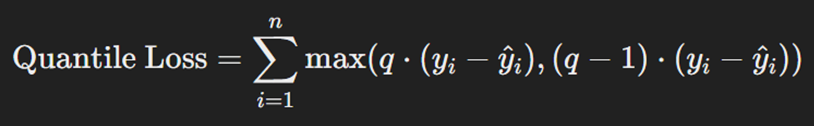
که در آن n تعداد کل داده‌ها، y_i مقدار واقعی خروجی و ŷ_i مقدار پیش‌بینی‌شده آن برای داده iام است؛ همچنین q چندک مدنظر (مثلاً برای میانه ۰.۵) است.

تابع هزینه کاتربار به‌ازای هر داده به‌صورت شرطی عمل می‌کند:

• اگر مقدار پیش‌بینی‌شده کمتر از مقدار واقعی باشد (ŷ_i < y_i)، هزینه برابر با q برابر اختلاف است.
• اگر مقدار پیش‌بینی‌شده بیشتر از مقدار واقعی باشد (ŷ_i > y_i)، هزینه برابر با 1-q برابر اختلاف است.

برای درک بهتر عملکرد این تابع هزینه یک مثال برای دو دهک خاص می‌زنیم:

پیش‌بینی پایین‌ترین دهک (۱۰ درصد پایینی)

برای اینکه مدل پایین‌ترین دهک داده‌ها را پیش‌بینی کند، q را برابر با ۰.۱ قرار می‌دهیم؛ در این حالت:

• اگر  ŷ_i < y_i، هزینه برابر با (y_i – ŷ_i)۰.۱ خواهد بود.
• اگر ŷ_i > y_i، هزینه برابر با (y_i – ŷ_i) ۰.۹- یا (ŷ_i – y_i) ۰.۹ خواهد بود.

این به‌آن معناست که مدل برای پیش‌بینی مقدارهای پایین‌تر از مقدار واقعی وزن کمتری (۰.۱) می‌دهد، اما برای پیش‌بینی مقادیر بالاتر از مقدار واقعی جریمه بیشتری (۰.۹) اعمال می‌کند. این ویژگی باعث می‌شود که مدل به‌طور عمده بر پیش‌بینی مقادیر پایین‌تر تمرکز کند و به‌این ترتیب، پایین‌ترین دهک داده‌ها را بهتر پیش‌بینی کند.

پیش‌بینی بالاترین دهک (۱۰ درصد بالایی)

برای اینکه مدل بالاترین دهک داده‌ها را پیش‌بینی کند،  q را برابر با ۰.۹ قرار می‌دهیم. در این حالت:

• اگر  ŷ_i < y_i، هزینه برابر با (y_i – ŷ_i)۰.۹ خواهد بود.
• اگر ŷ_i > y_i، هزینه برابر با (y_i – ŷ_i) ۰.۱- یا (ŷ_i – y_i) ۰.۱ خواهد بود.

این به‌آن معناست که مدل برای پیش‌بینی مقدارهای پایین‌تر از مقدار واقعی وزن بیشتری (۰.۹) می‌دهد، اما برای پیش‌بینی مقدارهای بالاتر از مقدار واقعی جریمه کمتری (۰.۱) اعمال می‌کند. این ویژگی به این می‌انجامد که مدل به‌طور عمده بر پیش‌بینی مقدارهای بالاتر تمرکز کند و به‌این ترتیب، بالاترین دهک داده‌ها را بهتر پیش‌بینی کند.

به‌طور کلی، تابع هزینه کاتربار با استفاده از فرمول‌های ارائه‌شده مدل را قادر می‌کند تا پیش‌بینی‌های دقیقی برای بخش‌های خاصی از توزیع داده‌ها انجام دهد. با تنظیم مقدار q می‌توان مدل را به‌گونه‌ای تنظیم کرد که به پیش‌بینی مقدارهای واقع در چندک‌های مختلف توزیع داده‌ها بپردازد.

پیاده‌سازی در پایتون

با این کد از تابع هزینه Quantile Loss برای برای محاسبه میزان خطا برحسب وزن‌ها استفاده می‌کنیم:

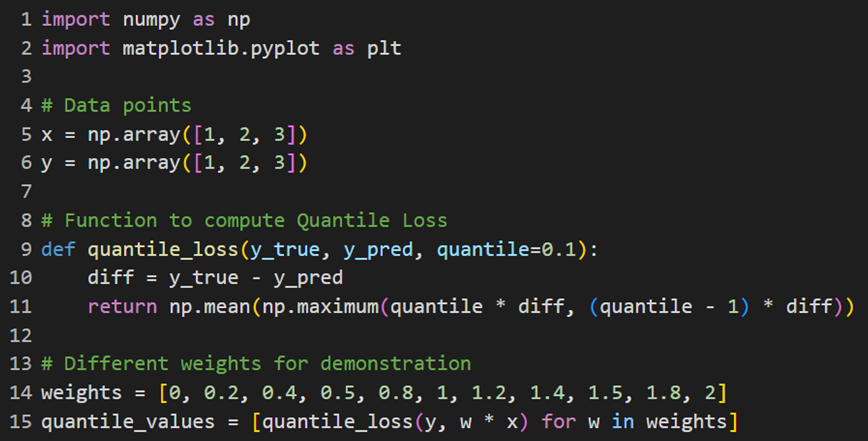
برای ترسیم نمودارهای این قسمت، با یک تغییر جزئی در کدهای مربوط ترسیم توابع قبلی، این خروجی را می‌گیریم که نشان می‌دهد چگونه مقدارهای خطا با تغییر وزن‌ها تغییر می‌کنند:

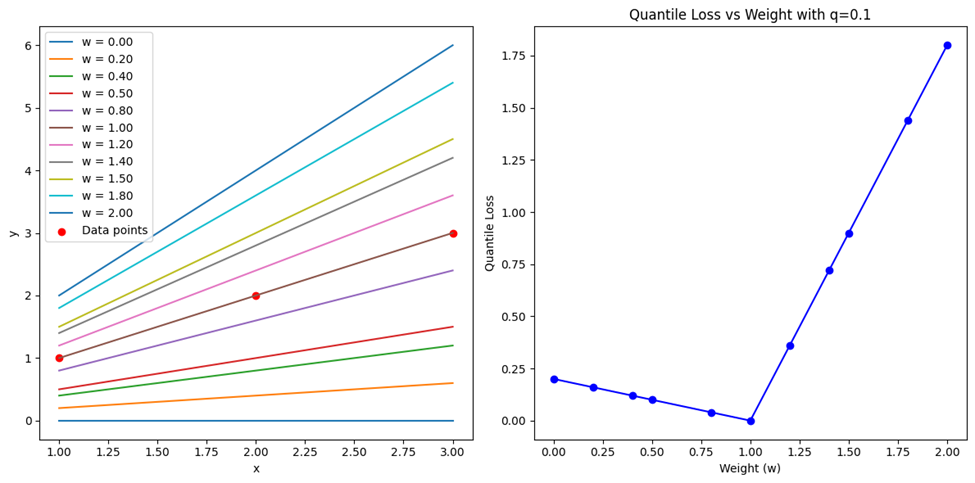
استفاده از Quantile Loss در کتابخانه‌های معروف

تنها کتابخانه‌ای که تابع هزینه کاتربار را به‌صورت ازپیش‌تعریف‌شده در خود تعبیه کرده سایکیدلرن است. در دیگر فریم‌ورک‌های ماشین لرنینگ باید این تابع را به‌صورت دستی تعریف کنیم:

Sklearn

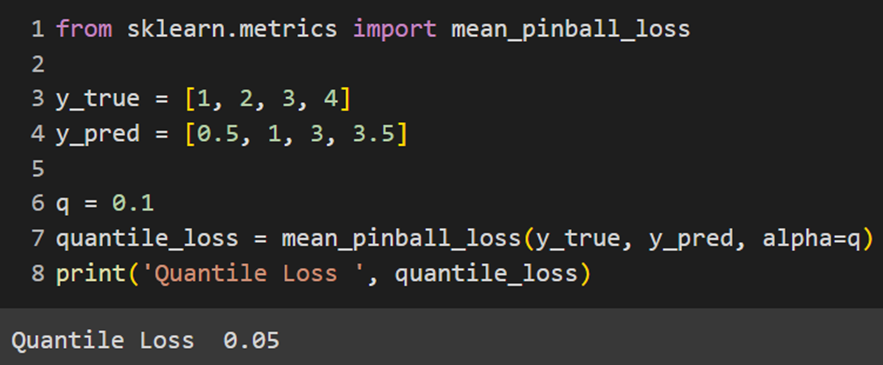
Keras

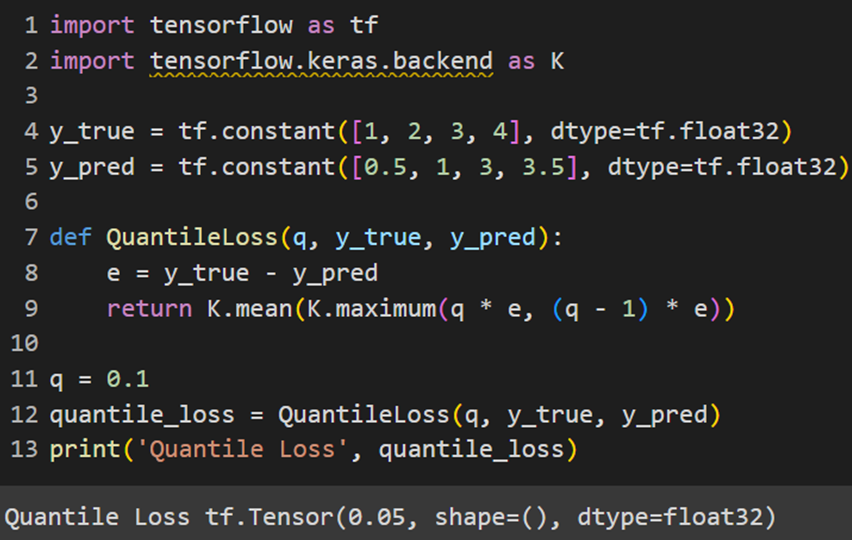
PyTorch

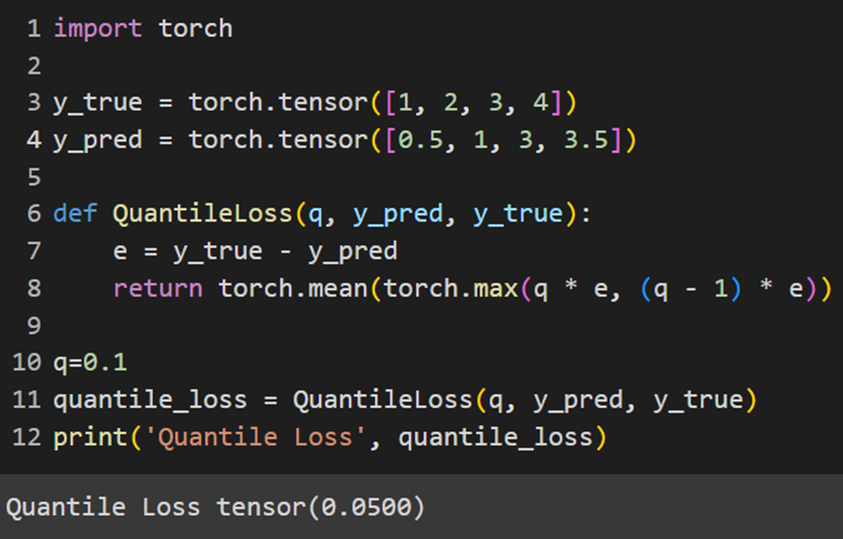
Jax

MXNet

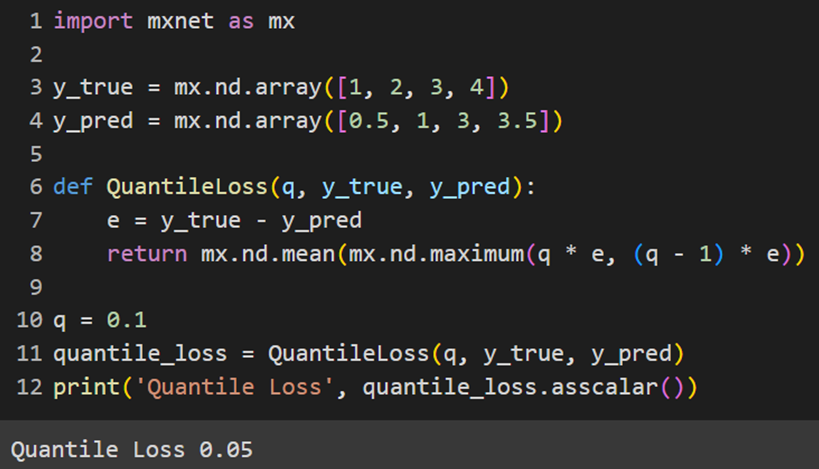
تابع هزینه کراس انتروپی

 تابع هزینه کراس انتروپی یا Cross-Entropy Loss (CE) در مسئله‌های دسته‌بندی کاربرد زیادی دارد. این تابع میزان نادرستی پیش‌بینی‌های مدل را در تعیین کلاس‌ها اندازه‌گیری می‌کند. Cross-Entropy Loss به‌دلیل کارایی بالا در مسائل دسته‌بندی باینری و چندکلاسه یکی از محبوب‌ترین توابع هزینه در یادگیری ماشین است. این تابع به‌ویژه در شبکه‌های عصبی و یادگیری عمیق استفاده می‌شود و به بهبود عملکرد مدل‌ها کمک می‌کند. ما دو نوع تابع کراس انتروپی داریم:

تابع هزینه کراس انتروپی دودویی

تابع هزینه کراس انتروپی دودویی یا Binary Cross-Entropy Loss (BCE) برای مسئله‌های دسته‌بندی باینری استفاده می‌شود، یعنی زمانی که فقط دو کلاس داریم (مثلاً بله یا خیر، درست یا نادرست). در BCE از این فرمول برای محاسبه هزینه استفاده می‌شود:

در اینجا y_i نشان‌دهنده برچسب واقعی و ŷ_i احتمال پیش‌بینی‌شده توسط مدل برای داده iام است، علامت سیگما روی n یعنی ما جمعا n داده داریم. هدف از استفاده این فرمول کمینه‌کردن اختلاف میان برچسب‌های واقعی و احتمالات پیش‌بینی شده است.

توضیح و تعبیر شهودی این تابع هزینه در کلاس علم داده مقدماتی استاد شکرزاد آمده است:

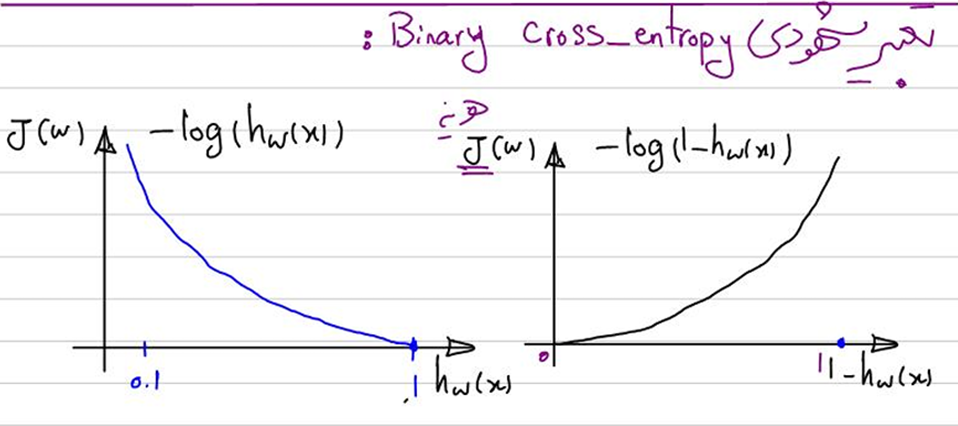
شکل سمت راست مربوط به حالتی است که برچسب (Label) صفر است و ضریب جمله اول فرمول ارائه‌شده صفر می‌شود و از میان می‌رود، اما ضریب جمله دوم یک می‌شود و باقی می‌ماند؛ به‌این ترتیب، اگر مدل داده را به دسته ۱ نسبت دهد، تابع هزینه عددی بسیار بزگ و نزدیک به‌بی‌نهایت می‌شود، اما اگر آن را به‌دسته ۰ نسبت دهد، هزینه‌ای بسیار پایین و نزدیک به صفر برایش محاسبه می‌شود؛ برعکس، در شکل سمت چپ که مربوط به حالتی است که برچسب یک است و ضریب جمله اول فرمول یک می‌شود و ضریب جمله دوم صفر. در این حالت اگر مدل داده را به‌دسته ۰ نسبت دهد، تابع هزینه عددی بسیار بزرگ اما اگر آن را یه‌دسته یک متعلق بداند، تابع هزینه مطابق انتظار عددی نزدیک به صفر را نشان خواهد داد.

نحوه استفاده از BCE در کتابخانه‌های معروف

بیشتر کتابخانه‌های ماشین لرنینگ پایتون تابع هزینه کراس انتروپی دودویی را به‌صورت پیش‌فرض در خود تعریف کرده‌اند. در ادامه نحوه استفاده از این تابع هزینه را در هر یک از فریم‌ورک‌ها بررسی می‌کنیم:

Sklearn

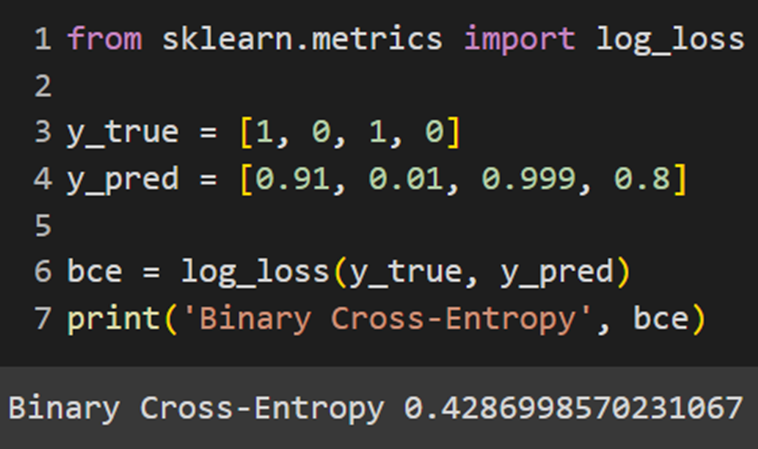
Keras

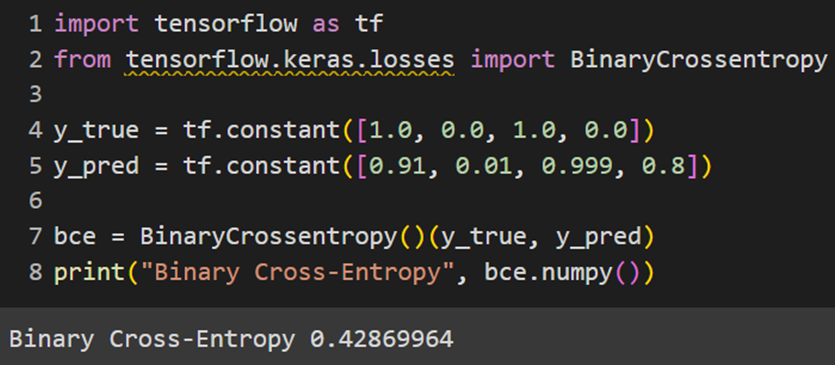
PyTorch

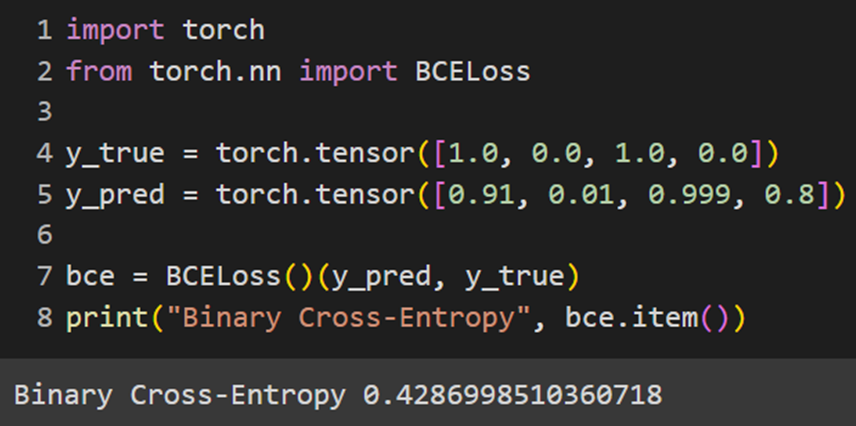
Jax

این تابع به‌صورت ازپیش‌ساخته‌شده در Jax وجود ندارد؛ لذا باید خودمان آن را تعریف کنیم:

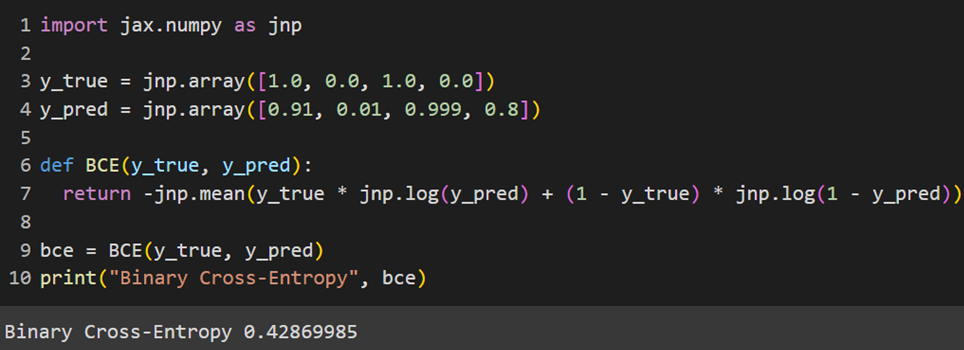
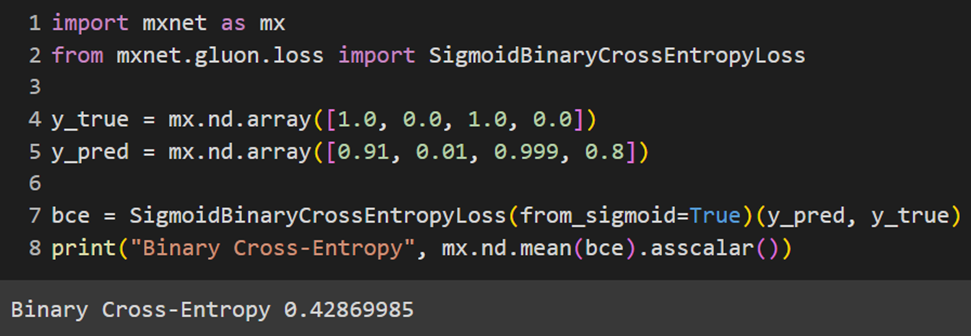
MXNet

تابع هزینه کراس انتروپی طبقه‌بندی‌شده

تابع هزینه کراس انتروپی طبقه‌بندی‌شده یا Categorical Cross-Entropy Loss (CCE) این نوع تابع هزینه برای مسائل دسته‌بندی چندکلاسه استفاده می‌شود، یعنی زمانی که بیش از دو کلاس داریم. در CCE از این فرمول برای محاسبه هزینه استفاده می‌شود:

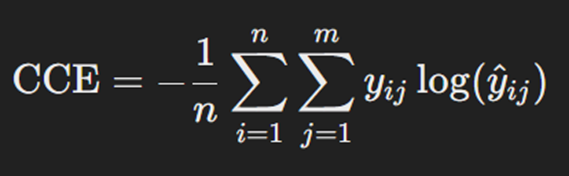
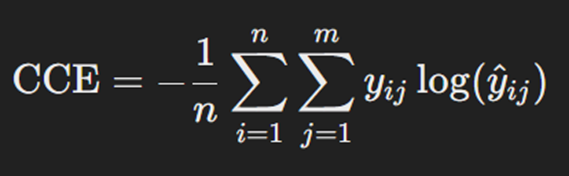
در اینجا y_ij نشان‌دهنده برچسب واقعی داده iام از کلاس jام است. علامت سیگما روی متغیرهای n و m یعنی ما درمجموع n داده و m کلاس برای دسته‌بندی این داده‌ها داریم. ŷ_ij هم​ احتمال پیش‌بینی‌شده توسط مدل برای داده iام از کلاس jام است. این فرمول کمک می‌کند تا مدل بتواند تفاوت میان پیش‌بینی‌ها و برچسب‌های واقعی را کاهش دهد و دقت کلی مدل را افزایش دهد.

تعبیر شهودی ارائه‌شده در قسمت تابع هزینه کراس انتروپی دودویی را می‌توان به‌ این‌بخش هم تعمیم داد.

نحوه استفاده از CCE در کتابخانه‌های معروف

بیشتر کتابخانه‌های ماشین لرنینگ پایتون تابع هزینه CCE را به‌صورت پیش‌فرض در خود تعریف کرده‌اند. در ادامه نحوه استفاده از این تابع هزینه را در هر یک از فریم‌ورک‌ها بررسی می‌کنیم:

Sklearn

در سایکیدلرن تابعی برای محاسبه تابع هزینه کراس انتروپی طبقه‌بندی‌شده وجود ندارد و باید خودمان آن را بسازیم:

Keras

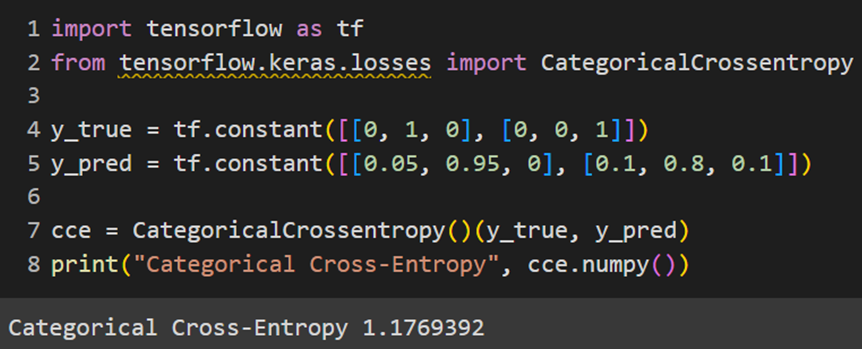
PyTorch

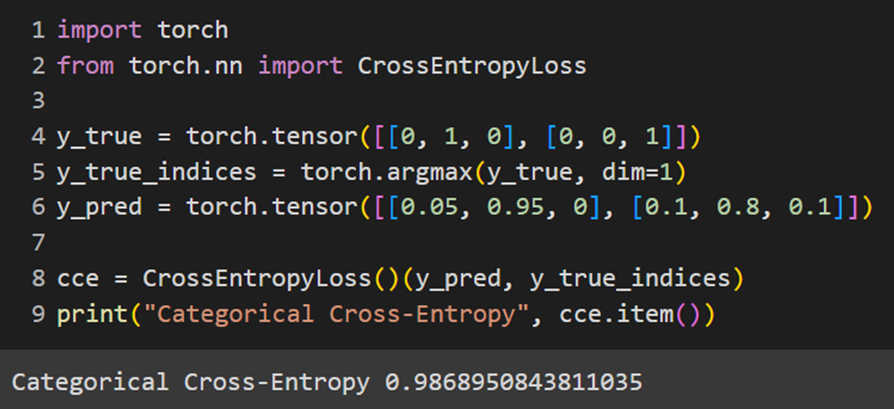
علت اختلافی که در نتیجه خروجی تابع CCE پایتورچ با کراس دیده می‌شود این است که این تابع هزینه در پایتورچ بعد از گرفتن مقدار پیش‌بینی‌شده، با فرض غیراحتمالی‌بودن خروجی مدل (یعنی همان logit)، ابتدا آن را از یک تابع Softmax رد می‌کند و سپس فرمول کراس انتروپی را روی آن اعمال می‌کند، اما در فریم‌ورک کراس این اتفاق نمی‌افتد و خروجی مدل مستقیما در فرمول کراس انتروپی استفاده می‌شود. تفاوت دیگر این تابع با تابع CCE فریم‌ورک کراس این است که لیبل‌ها را به‌صورت One-Hotشده دریافت نمی‌کند؛ به‌همین دلیل y_true که به‌صورت One-Hot تعریف‌شده است، ابتدا با تابع argmax به‌صورت یک فهرست دومولفه‌ای درمی‌‌آید که عضو اول آن ۱ و عضو دوم آن ۲ به‌معنای کلاس‌های ۱ و ۲ است؛ سپس این خروجی به‌عنوان لیبل به تابع هزینه مدنظر داده خواهد شد.

Jax

در این فریم‌ورک تابع کراس انتروپی چندتایی نیز به‌صورت پیش‌فرض تعریف نشده است؛ پس خودمان آن را می‌سازیم:

MXNet

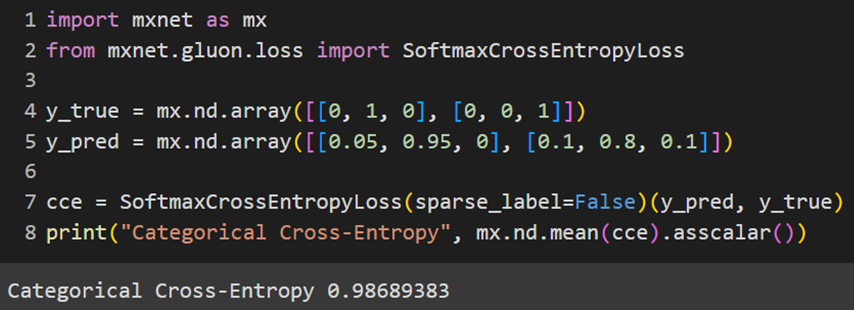
توضیحاتی که درمورد این تابع هزینه در قسمت مربوط به کتابخانه پایتورچ دادیم برای MXNet هم صادق است.

تابع هزینه هینج

Hinge Loss به‌ویژه در الگوریتم‌های ماشین بردار پشتیبان (SVM) استفاده می‌شود. این تابع برای مسئله‌های دسته‌بندی دوکلاسه مناسب است. Hinge Loss با تأکید بر جداسازی بهینه کلاس‌ها به مدل کمک می‌کند تا دقت بالاتری در پیش‌بینی دسته‌ها داشته باشد. این تابع برای مسائلی که به دقت بالا در دسته‌بندی نیاز دارند بسیار مناسب است. فرمول این تابع به‌این صورت محاسبه می‌شود:

که در آن n تعداد کل داده‌ها، y_i مقدار واقعی خروجی (که مقدارش یا ۱+ یا ۱- است) و ŷ_i مقدار پیش‌بینی‌شده آن برای داده iام است. در این تابع:

• اگر حاصل‌ضرب مقدار اصلی و پیش‌بینی‌شده برچسب بزرگ‌تر یا مساوی یک باشد، هزینه برابر با صفر خواهد بود، یعنی پیش‌بینی درست انجام شده است.
• اگر حاصل‌ضرب مقدار اصلی و پیش‌بینی‌شده برچسب کمتر از یک باشد، هزینه برابر 1-yi خواهد بود، یعنی پیش‌بینی نادرست انجام شده است.

این تابع هزینه به‌گونه‌ای طراحی شده است که تنها زمانی هزینه محاسبه می‌شود که پیش‌بینی مدل اشتباه باشد یا به‌اندازه کافی از خط جداساز دور نباشد؛ به‌همین دلیل، هینج لاس به مدل کمک می‌کند تا مرز میان دسته‌ها را بهینه‌تر تعیین کند و درنهایت، مدل‌های دقیق‌تری بسازد.

پیاده‌سازی در پایتون

کد زیر به‌منظور نمایش نحوه عملکرد تابع هزینه هینج (Hinge Loss) در مسئله‌ی طبقه‌بندی باینری طراحی شده است. داده‌ها شامل مقدارهای یک ویژگی‌ (X) با برچسب‌های (y) ۱- و ۱+ هستند:

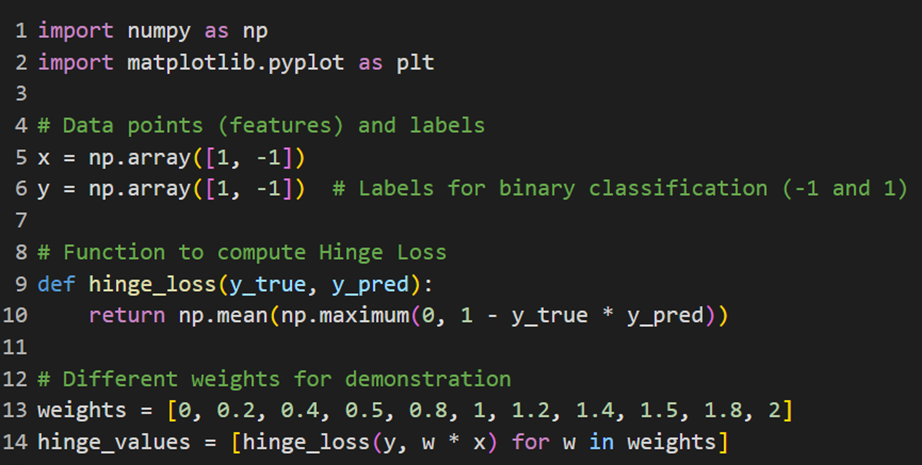
کد ترسیم نمودارهای مربوط به این تابع هزینه نیز با تغییری جزئی روی کدهای ترسیم نمودارهای توابع هزینه قبلی به دست می‌آید. خروجی را می‌توانید در این شکل ببینید:

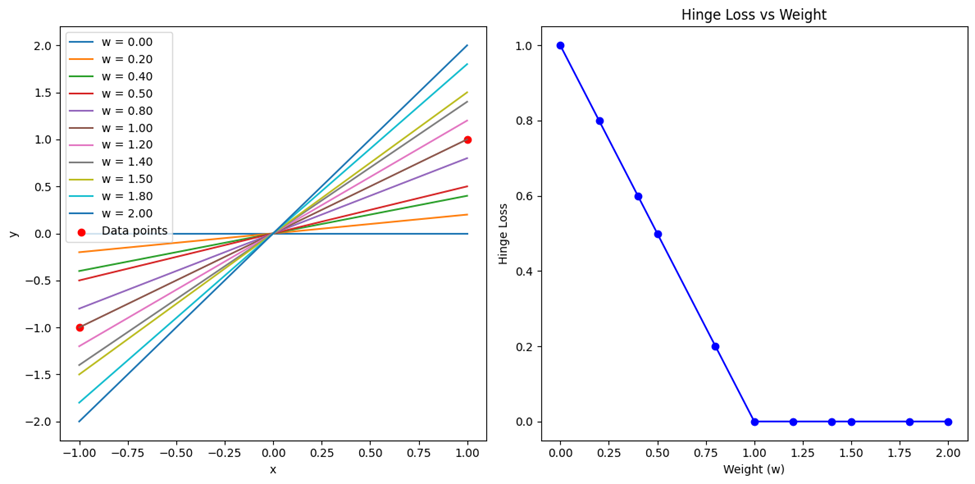
همان‌طور که مشاهده می‌کنید، در شکل سمت چپ با تغییر وزن، شیب خطوط طبقه‌بندی تغییر می‌کند. این نشان می‌دهد که وزن‌های مختلف می‌توانند تاثیر چشمگیری روی مرز تصمیم‌گیری مدل داشته باشند. نمودار سمت راست نیز هزینه Hinge را در مقایسه با وزن‌ها نشان می‌دهد. در ابتدا با افزایش وزن هزینه Hinge کاهش می‌یابد تا به یک مقدار حداقلی برسد و سپس ثابت می‌ماند.

استفاده از Hinge Loss در کتابخانه‌های معروف

برخی کتابخانه‌های معروف ماشین لرنینگ پایتون این تابع هزینه را به‌طور پیش‌فرض در خود تعریف کرده‌اند. نحوه استفاده از تابع هزینه هینج در فریم‌ورک‌های مختلف را در ادامه می‌بینید:

Skleran

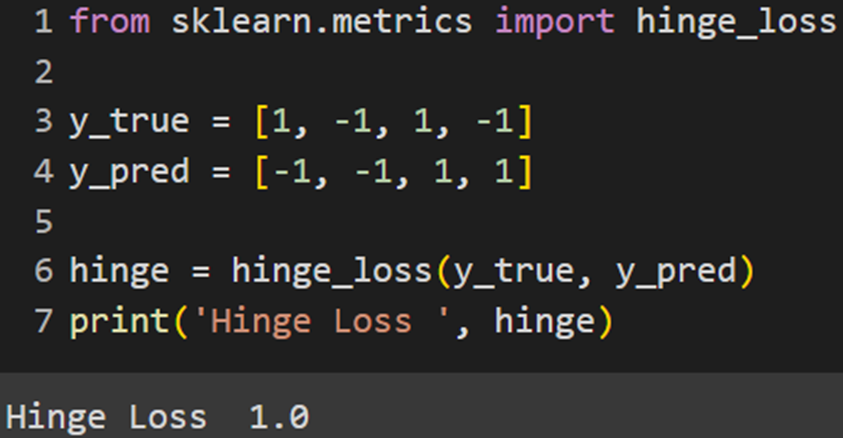
Keras

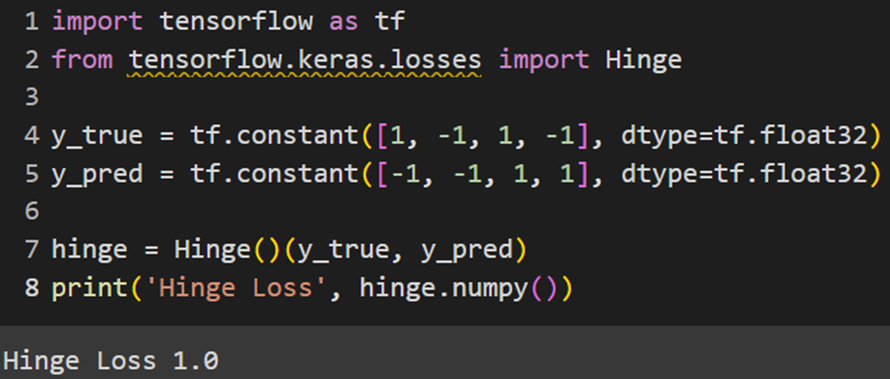
PyTorch

پایتورچ این تابع هزینه را به‌صورت پیش‌فرض در خود تعریف نکرده است؛ البته یک تابع به‌نام HingeEmbeddingLoss در کلاس torch.nn این فریم‌ورک وجود دارد، اما فرمول محاسبه آن کمی با فرمول اصلی تابع هینج متفاوت است. برای تعریف این تابع هزینه در پایتورچ به‌این شکل عمل می‌کنیم:

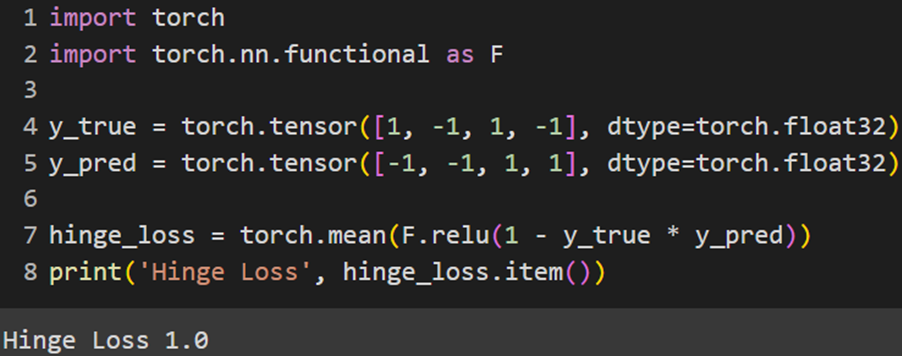
Jax

این کتابخانه مانند پایتورچ تابع هزینه هینج را به‌صورت ازپیش‌تعریف‌شده ندارد و باید آن را به‌این صورت استفاده کنیم:

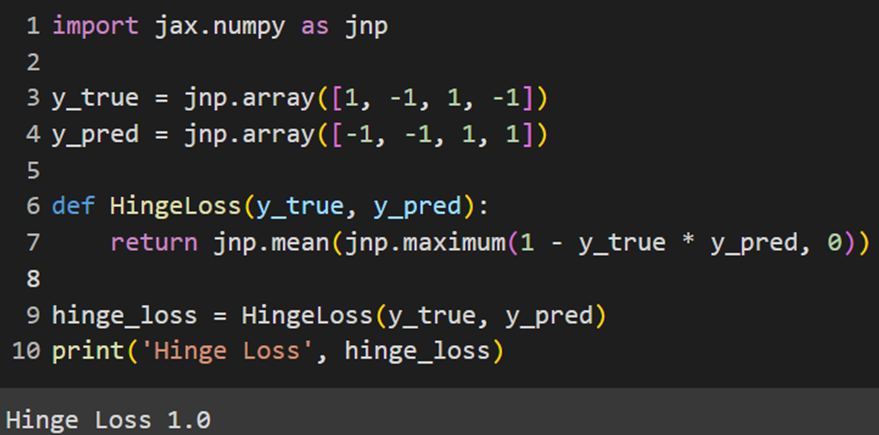
MXNet

تابع هزینه نمایی

تابع هزینه نمایی در الگوریتم‌های Boosting، مانند AdaBoost، کاربرد دارد. این تابع خطاهای پیش‌بینی را به‌صورت نمایی افزایش می‌دهد، به‌این معنا که خطاهای بزرگتر در به‌روزرسانی مدل تاثیر بیشتری می‌گذارند. Exponential Loss به این می‌انجامد که مدل به نمونه‌هایی که به‌سختی پیش‌بینی‌شدنی هستند بیشتر توجه کند. این ویژگی می‌تواند به بهبود دقت مدل بینجامد، اما ممکن است به این بینجامد که مدل به داده‌های پرت بیش‌ازحد حساس شود. فرمول این تابع هزینه به‌این شکل است:

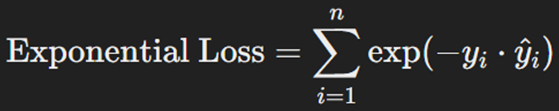
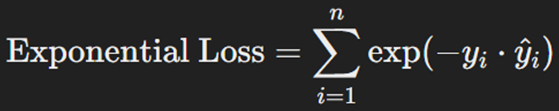
که در آن n تعداد کل داده‌ها، y_i مقدار واقعی خروجی (که مقدارش یا ۱+ یا ۱- است) و ŷ_i مقدار پیش‌بینی‌شده آن برای داده iام است.

این تابع هزینه به‌دلیل استفاده از تابع نمایی، به خطاهای بزرگ، به‌شدت بیشتر وزن می‌دهد. این ویژگی به این می‌انجامد که مدل به نمونه‌هایی که به‌اشتباه دسته‌بندی شده‌اند توجه بیشتری کند و درنتیجه، دقت کلی مدل بهبود یابد.

پیاده‌سازی در پایتون

برای پیاده‌سازی تابع هزینه نمایی (Exponential Loss) در مسئله طبقه‌بندی باینری از این کد استفاده می‌کنیم:

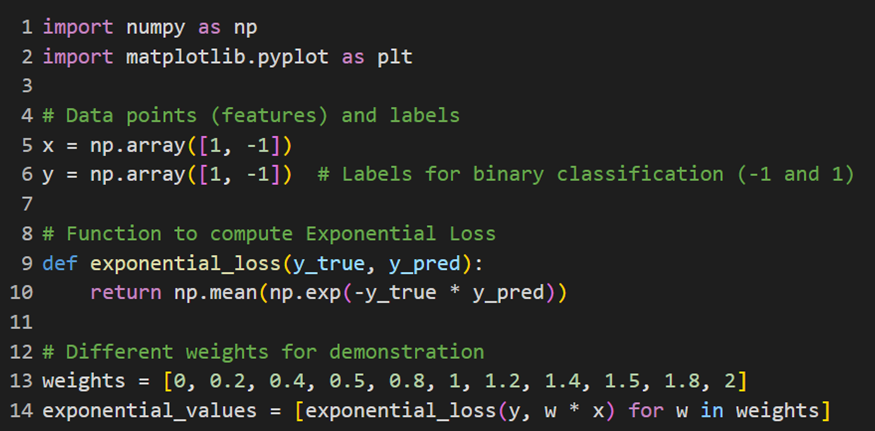
نمودارهای مربوط نیز مشابه کد قسمت‌های قبل و با تغییری جزئی به‌این شکل درمی‌آید:

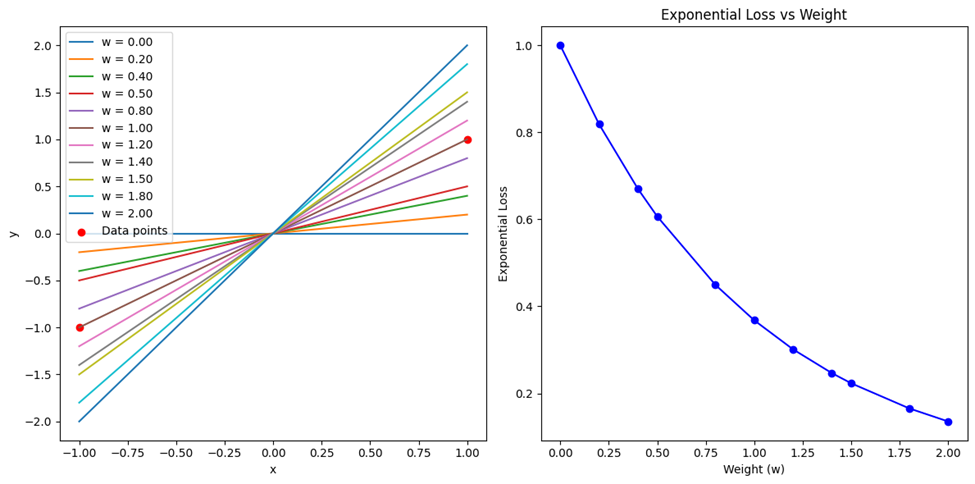
نمودار سمت چپ خطوط طبقه‌بندی را نشان می‌دهد که با تغییر وزن، شیب خطوط تغییر می‌کند و تأثیر وزن‌های مختلف بر مرز تصمیم‌گیری مدل را نشان می‌دهد. نمودار سمت راست مقدار هزینه نمایی را در مقایسه با وزن‌ها نشان می‌دهد. این نمودارها به‌خوبی نشان می‌دهند که چگونه وزن‌های مختلف می‌توانند بر مرز تصمیم‌گیری و هزینه نمایی تأثیر قابل‌توجهی بگذارند.

استفاده از تابع هزینه نمایی در کتابخانه‌های معروف

تابع هزینه نمایی در بسیاری از کتابخانه‌های یادگیری ماشین مانند Scikit-learn ،Keras ،PyTorch ،JAX و MXNet به‌صورت پیش‌فرض وجود ندارد. این تابع ممکن است در برخی کاربردهای خاص یا زمینه‌های تحقیقاتی استفاده شوند، اما برای کاربردهای عمومی و گسترده یادگیری ماشین، دیگر توابع هزینه ترجیح داده می‌شوند؛ بااین‌حال ما برای کامل‌بودن این آموزش، نحوه پیاده‌سازی آن را در هر یک از فریم‌ورک‌های نام‌برده نشان خواهیم داد:

Sklearn

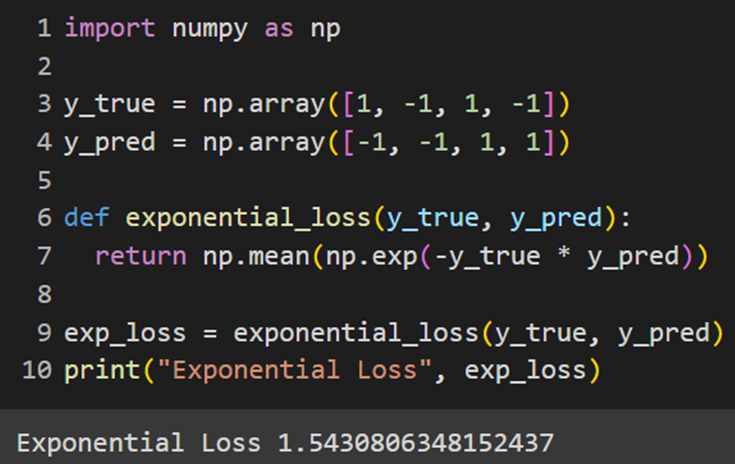
Keras

PyTorch

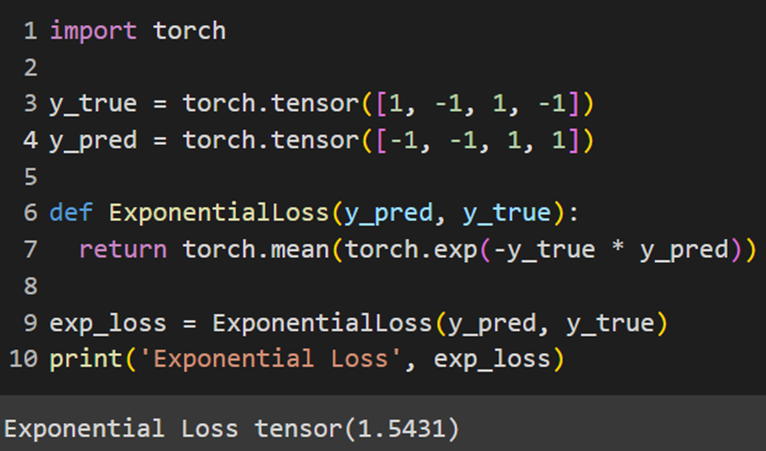
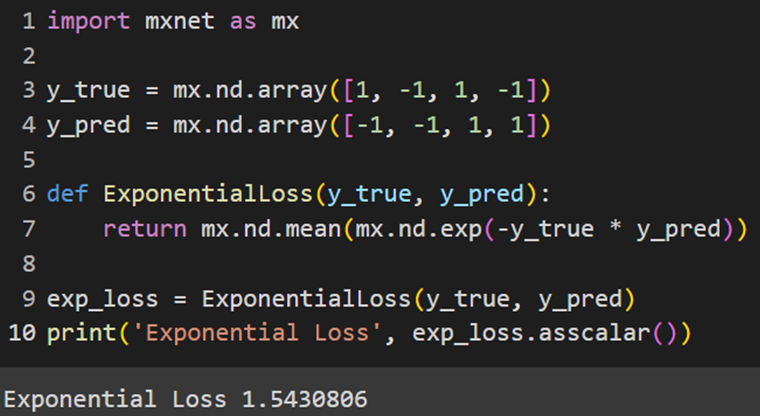
Jax

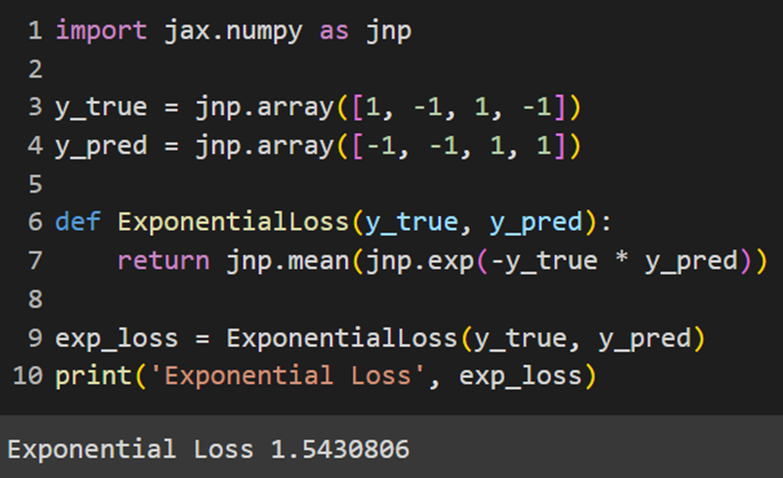
MXNet

تابع هزینه واگرایی کولبک-لایبلر

Kullback-Leibler Divergence (KL Divergence) برای اندازه‌گیری تفاوت میان دو توزیع احتمال استفاده می‌شود. KL Divergence به مدل کمک می‌کند تا توزیع پیش‌بینی‌شده را به توزیع هدف نزدیک کند. فرمول این تابع هزینه به‌این صورت است:

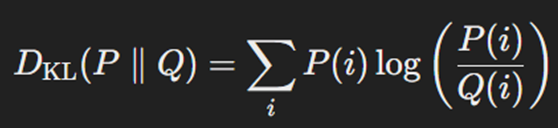
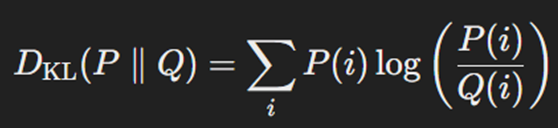
در این فرمول:

• P توزیع احتمال مرجع (توزیع واقعی) است.
• Q توزیع احتمال تقریبی (توزیع پیش‌بینی‌شده توسط مدل) است.
• P(i) احتمال وقوع حالت i در توزیع P است.
• Q(i) احتمال وقوع حالت i در توزیع Q است.

واگرایی کولبک-لایبلر همیشه غیرمنفی است و فقط زمانی برابر صفر می‌شود که دو توزیع P و Q کاملاً یکسان باشند. این ویژگی نشان می‌دهد که چقدر توزیع پیش‌بینی‌شده از توزیع واقعی دور است.

این تابع، به‌ویژه، در مدل‌های مولد مانند VAE (Variational Autoencoders) کاربرد دارد. در این مدل‌ها واگرایی کولبک-لایبلر برای اندازه‌گیری فاصله میان توزیع پیش‌بینی‌شده توسط مدل و توزیع مرجع استفاده می‌شود. این معیار به مدل کمک می‌کند تا توزیع پیش‌بینی‌شده را به توزیع واقعی نزدیک کند که این امر در بهبود کیفیت نمونه‌های تولیدشده توسط مدل مؤثر است.

نحوه استفاده از KL Divergence در کتابخانه‌های معروف

برخی کتابخانه‌های معروف پایتونی مربوط به ماشین لرنینگ این تابع هزینه را به‌صورت ازپیش‌ساخته‌شده در خود تعریف کرده‌اند. نحوه استفاده از این تابع هزینه را در هر یک از این کتابخانه‌ها و فریم‌ورک‌ها می‌بینید:

Sklearn

Keras

PyTorch

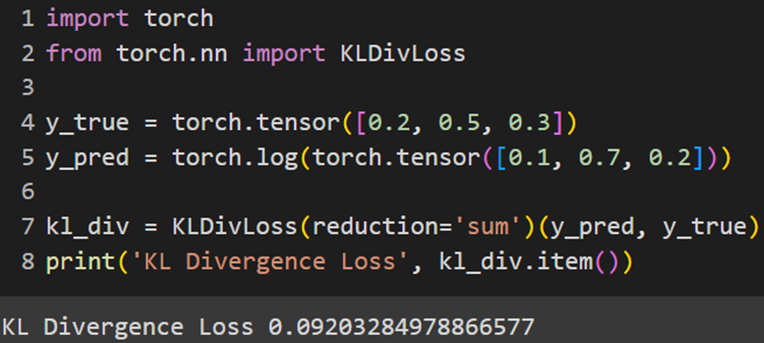
Jax

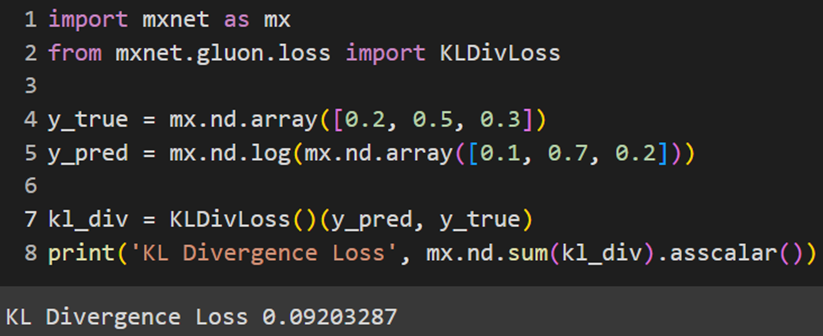
MXNet

نقش توابع هزینه در یادگیری ماشین

توابع هزینه در تمامی الگوریتم‌های یادگیری ماشین کاربرد دارند. از رگرسیون خطی گرفته تا شبکه‌های عصبی پیچیده، همه، به این توابع وابسته هستند تا عملکرد خود را بهینه کنند. به‌طور کلی، بدون استفاده از تابع هزینه، بهبود مدل‌ها و دستیابی به نتایج دقیق و معتبر غیرممکن است. توابع هزینه به ما این امکان را می‌دهند تا مدل‌های خود را بهبود دهیم و عملکرد آن‌ها را بهینه‌سازی کنیم.

ارزیابی مدل‌ها

توابع هزینه به‌عنوان معیارهایی برای ارزیابی عملکرد مدل‌ها استفاده می‌شوند. آن‌ها با اندازه‌گیری اختلاف میان خروجی‌های پیش‌بینی‌شده و مقادیر واقعی کمک می‌کنند تا کیفیت مدل‌ها سنجیده شود.

راهنمای بهینه‌سازی

توابع هزینه به الگوریتم‌های بهینه‌سازی کمک می‌کنند تا پارامترهای مدل را تنظیم کنند. با کمینه‌سازی تابع هزینه، الگوریتم‌ها می‌توانند پارامترهایی پیدا کنند که عملکرد مدل را بهینه کنند.

شناسایی داده‌های پرت

توابع هزینه می‌توانند به شناسایی داده‌های پرت کمک کنند. داده‌هایی که افزایش زیاد تابع هزینه را رقم می‌زنند ممکن است پرت باشند و می‌توانند برای بهبود مدل حذف یا بررسی شوند.

مقایسه مدل‌ها

توابع هزینه امکان مقایسه مدل‌های مختلف را فراهم می‌کنند. با محاسبه و مقایسه مقدارهای تابع هزینه، می‌توان بهترین مدل را برای یک مسئله خاص انتخاب کرد.

تأثیر انتخاب تابع هزینه مناسب

انتخاب تابع هزینه مناسب روی نتایج مدل تأثیر زیادی می‌گذارد. هر تابع هزینه ویژگی‌ها و مزیت‌های خاص خود را دارد و برای کاربردهای مختلف بهینه است؛ برای مثال، در مسئله‌های رگرسیون استفاده از تابع هزینه مربعات خطا (MSE) معمول است، درحالی‌که در مسئله‌های دسته‌بندی، استفاده از تابع هزینه کراس انتروپی رایج‌تر است.

چالش‌ها و ملاحظات

استفاده از توابع هزینه در یادگیری ماشین و هوش مصنوعی با چالش‌ها و ملاحظه‌های مختلفی همراه است که در ادامه برخی از آن‌ها را بررسی می‌کنیم:

بیش‌برازش

استفاده نادرست از توابع هزینه می‌تواند به بیش‌برازش (Overfitting) بینجامد، جایی که مدل به‌خوبی داده‌های آموزش را پیش‌بینی می‌کند، اما در داده‌های جدید عملکرد خوبی ندارد.

پیچیدگی محاسباتی

برخی توابع هزینه محاسبات پیچیده‌ای دارند که می‌تواند زمان آموزش مدل را افزایش دهد. انتخاب توابع هزینه‌ای که هم بهینه باشند و هم محاسبات را ساده نگه دارند مهم است.

حساسیت به مقیاس داده‌ها

برخی توابع هزینه به مقیاس داده‌ها حساس هستند و ممکن است نیاز به نرمال‌سازی داده‌ها قبل از استفاده داشته باشند. این نکته باید در انتخاب و استفاده از توابع هزینه مدنظر قرار گیرد.

با درنظرگرفتن این نکته‌ها توابع هزینه ابزارهای قدرتمندی در یادگیری ماشین هستند که به بهبود و بهینه‌سازی مدل‌ها کمک می‌کنند. انتخاب دقیق و استفاده هوشمندانه از این توابع می‌تواند نتایج بهتری در مسئله‌های یادگیری ماشین به همراه داشته باشد.

جمع‌بندی

توابع هزینه نقش بسیار مهمی در فرایند آموزش و بهینه‌سازی مدل‌های یادگیری ماشین ایفا می‌کنند. از انتخاب تابع مناسب تا اعمال آن در بهینه‌سازی مدل، هر جزئی از این فرایند می‌تواند بر عملکرد نهایی مدل تأثیر زیادی بگذارد. با درک صحیح و استفاده بهینه از توابع هزینه، می‌توان به مدل‌هایی دقیق‌تر و کارآمدتر دست یافت که نیازهای پیچیده و متنوع دنیای واقعی را برآورده می‌کنند.

پرسش‌های متداول

تفاوت میان تابع هزینه و تابع هدف چیست؟

تابع هزینه میزان خطا یا انحراف پیش‌بینی‌های مدل از مقدارهای واقعی را اندازه‌گیری می‌کند، درحالی‌که تابع هدف بهینه‌سازی عملکرد مدل را با توجه به تابع هزینه هدایت می‌کند. تابع هدف معمولاً شامل تابع هزینه و دیگر محدودیت‌ها یا اهداف مرتبط با مدل است.

چرا با اینکه تابع هزینه Huber از مزیت‌های MSE و MAE بهره می‌برد و درعین‌حال عیب‌های آن‌ها را کاهش می‌دهد، بازهم از MAE و MSE بیشتر استفاده می‌شود؟

به‌رغم مزیت‌های Huber، فرمول‌های MSE و MAE بسیار ساده‌تر هستند؛ به‌همین‌دلیل، محاسبات آن‌ها در مقایسه با هوبر سریع‌تر است، به‌ویژه در مجموعه داده‌های بزرگ؛ علاوه‌براین هوبر به تنظیم یک پارامتر اضافی به‌نام آستانه (δ) نیاز دارد که ممکن است به تنظیم دستی و بهینه‌سازی بیشتری نیاز داشته باشد، درحالی‌که MSE  و MAE چنین نیازی ندارند.

آیا می‌توان از چندین تابع هزینه به‌طور همزمان استفاده کرد؟

بله، در برخی موارد می‌توان از ترکیب چندین تابع هزینه برای بهینه‌سازی مدل استفاده کرد. این رویکرد به‌ویژه در مدل‌های پیچیده و شبکه‌های عصبی عمیق معمول است، جایی که ممکن است ترکیب توابع هزینه مختلف به بهبود عملکرد کمک کند.

چگونه می‌توان تأثیر نویز داده‌ها را بر انتخاب تابع هزینه مدیریت کرد؟

برای داده‌های دارای نویز زیاد، استفاده از توابع هزینه‌ای مانند MAE یا Huber Loss که کمتر به خطاهای بزرگ حساس هستند، می‌تواند مفید باشد. این توابع به مدل کمک می‌کنند تا مقاومت بیشتری دربرابر نویز داشته باشند و عملکرد بهتری ارائه کنند.

تفاوت میان MSE و MAE چیست؟

MSE به خطاهای بزرگ حساس‌تر است و به‌دلیل محاسبه مربع خطاها، خطاهای بزرگ را بیشتر وزن می‌دهد، درحالی‌که MAE به خطاهای کوچک و بزرگ به‌طور مساوی پاسخ می‌دهد و میانگین قدر مطلق خطاها را اندازه‌گیری می‌کند.

یادگیری ماشین لرنینگ را از امروز شروع کنید!

دنیای داده‌ها جذاب است و دانستن علم داده، توانایی تحلیل داده‌، یا بازاریابی مبتنی بر داده، شما را برای فرصت‌های شغلی بسیاری مناسب می‌کند. فارغ از رشته‌ و پیش‌زمینه‌، می‌توانید حالا شروع کنید و از سطح مقدماتی تا پیشرفته بیاموزید. اگر دوست دارید به این حوزه وارد شوید، پیشنهاد می‌کنیم با کلیک روی این لینک قدم اول را همین حالا بردارید.

مشاوران کافه‌تدریس به شما کمک می‌کنند مسیر یادگیری برای ورود به این حوزه را شروع کنید:

دوره جامع دیتا ساینس و ماشین لرنینگ