الگوریتم ژنتیک (Genetic Algorithm) یک رویکرد بهینهسازی و جستوجوی احتمالی است که از فرایندهای طبیعی تکامل بیولوژیکی الهام گرفته است. این الگوریتم توانایی یافتن پاسخهای نزدیک به بهینه در مسائل پیچیدهای را دارد که شاید با روشهای سنتی حلشدنی نباشند. این روش در دهه ۱۹۷۰ مطرح شده و از آن زمان تاکنون در زمینههای گوناگونی ازجمله علم داده و مهندسی نرمافزار کاربرد داشته است. در این مطلب ما، ضمن بررسی مبانی موردنیاز، به پیادهسازی الگوریتم ژنتیک در پایتون و حل مسئله کولهپشتی صفر و یک بهکمک آن میپردازیم.
- 1. تاریخچه الگوریتم ژنتیک در پایتون
- 2. مفاهیم اصلی الگوریتم ژنتیک در پایتون
- 3. پیادهسازی الگوریتم ژنتیک در پایتون
- 4. تعریف مسئله کولهپشتی ۰ و ۱
- 5. حل مسئله کولهپشتی ۰ و ۱ با استفاده از الگوریتم ژنتیک
- 6. بررسی صحت جواب الگوریتم ژنتیک با استفاده از برنامهنویسی پویا
- 7. چالشها و محدودیتهای الگوریتم ژنتیک در پایتون
- 8. خلاصه مطلب
-
9.
سوالات متداول
- 9.1. الگوریتم ژنتیک در پایتون چگونه در مسائل بهینهسازی استفاده میشود؟
- 9.2. چه فرایندهایی در الگوریتم ژنتیک وجود دارد و نقش هر یک چیست؟
- 9.3. چرا الگوریتم ژنتیک در پایتون برای حل مسئله کولهپشتی مناسب است؟
- 9.4. چگونه میتوان کارایی الگوریتم ژنتیک را در حل مسائل بهینهسازی افزایش داد؟
- 9.5. تأثیر پیشرفتهای فناوری اطلاعات بر الگوریتم ژنتیک چیست؟
- 10. یادگیری تحلیل داده و ماشین لرنینگ را از امروز شروع کنید!
تاریخچه الگوریتم ژنتیک در پایتون
جان هالند و همکارانش الگوریتمهای ژنتیک را در دهه ۱۹۷۰ در دانشگاه میشیگان توسعه دادند. این روشها بهسرعت توجه دانشمندان را در علوم کامپیوتر به خود جلب کرد. امروزه با پیشرفت تکنولوژی و دسترسی آسان به منابع محاسباتی قدرتمند، الگوریتمهای ژنتیک در حال پیشرفت و کاربرد گستردهتری هستند.
مفاهیم اصلی الگوریتم ژنتیک در پایتون
پیش از پیادهسازی الگوریتم ژنتیک در پایتون لازم است با مفاهیم اصلی این الگوریتم آشنا شویم:
ژنوم و کروموزومها
در الگوریتمهای ژنتیک هر راهحل ممکن بهصورت یک کروموزوم نمایش داده میشود که از یک سری ژن (Gene) تشکیل شده است. هر ژن در این کروموزوم میتواند یک ویژگی خاص از مسئله را نشان دهد.
تابع هدف و برازش
تابع هدف که گاهی بهعنوان تابع برازش شناخته میشود برای ارزیابی هر کروموزوم به کار میرود. این تابع میزان موفقیت هر راهحل را در حل مسئله مدنظر ارزیابی میکند.
عملگرها در الگوریتم ژنتیک
- جهش (Mutation): تغییرات تصادفی در ژنهای یک کروموزوم که به تنوع ژنتیکی کمک میکند.
- تلاقی (Cross Over): ترکیب ویژگیهای دو کروموزوم والد برای تولید فرزندان.
- انتخاب (Selection): انتخاب کروموزومهایی که براساس تابع برازش بهتر عمل میکنند برای تولید نسل بعدی.
پیادهسازی الگوریتم ژنتیک در پایتون
در این قسمت با پیادهسازی ساده الگوریتم ژنتیک در پایتون آشنا میشویم و در ادامه با دانشی که کسب میکنیم مسئله معروف کولهپشتی ۰ و ۱ را با استفاده از الگوریتم ژنتیک حل میکنیم.
فراخوانی کتابخانههای موردنیاز


کتابخانه random برای تولید اعداد تصادفی و انجامدادن انتخابهای تصادفی استفاده میشود که برای طبیعت احتمالی الگوریتمهای ژنتیکی ضروری است.
کتابخانه numpy در این کد عمدتاً برای تابع argmax آن استفاده میشود که در یافتن شاخص بیشترین مقدار در یک آرایه بسیار کارآمد است.
تابع مقداردهی اولیه جمعیت


هدف از تعریف این تابع مقداردهی اولیه جمعیتی از افراد است که هر فرد بهصورت فهرستی از بیتها (صفر یا یک) نمایش داده میشود.
در این تابع:
- pop_size تعداد کل افراد در جمعیت است.
- genome_size تعداد بیتها در هر فرد یا کروموزوم است که اندازه ژنوم را تعیین میکند.
- random.choices(range(2), k=genome_size) برای هر فرد، یک فهرست تصادفی از صفرها و یکها تولید میکند که نشاندهنده ژنهای آن فرد است.
تابع محاسبه برازندگی


تابع برازندگی تعیین میکند هر فرد چقدر خوب است. میزان خوببودن داشتن تعداد یکهای بیشتر است؛ بههمین دلیل، از تابع مجموعگیری (sum) روی بیتهای هر فرد استفاده شده است.
در این تابع:
- individual یک فرد در جمعیت است که بهصورت فهرستی از بیتها نمایش داده شده است.
- sum(individual) مجموع بیتهای یک در کروموزوم است که نشاندهنده میزان خوب بودن فرد است.
تابع انتخاب


هدف این تابع انتخاب والدین برای تولید نسل بعدی از طریق روش تورنمنت است.
در این تابع:
- population جمعیت فعلی است.
- fitnesses فهرستی از مقادیر برازندگی برای هر فرد در جمعیت است.
- tournament انتخاب تصادفی سه فرد از جمعیت است.
- np.argmax(tournament_fitnesses) یافتن شاخص فرد با بالاترین برازش در تورنمنت است.
- population[winner_index] فرد برنده را بهعنوان والد بازمیگرداند.
تابع تلاقی


هدفاین تابع تولید دو فرزند از دو والد با ترکیب بخشهایی از کروموزومهای آنهاست.
در این تابع:
- parent1 و parent2 دو والدی هستند که برای تلاقی انتخاب شدهاند.
- xo_point نقطه تقسیم تصادفی در کروموزوم است که بعد از آن بخشهای کروموزومها تعویض میشوند.
تابع جهش


هدف از این تابع افزودن تنوع ژنتیکی به جمعیت ازطریق تغییر تصادفی بیتهاست.
در این تابع:
- individual فردی است که جهش خواهد کرد.
- random.random() > rate یعنی با احتمال rate مشخصشده هر بیت میتواند جهش کند و مقدار آن تغییر کند (از ۰ به ۱ یا برعکس).
اجرای الگوریتم ژنتیک در پایتون
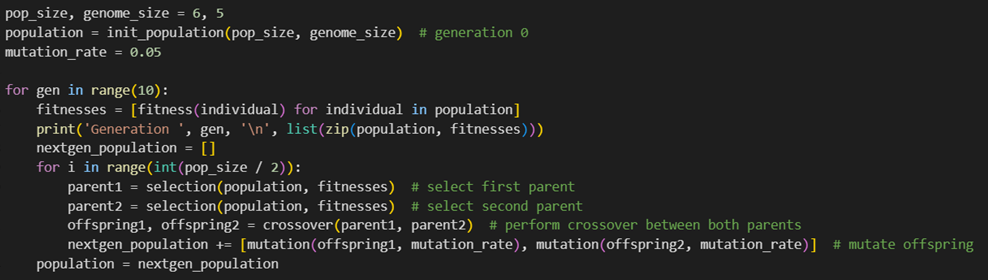

در این کد:
- خط اول مشخص میکند که جمعیت شامل ۶ فرد است و هر فرد دارای یک ژنوم (کروموزوم) با اندازه ۵ بیت است.
- population جمعیت اولیه را با استفاده از تابع تعریفشده init_population مقداردهی میکند که در آن کروموزوم هر فرد بهصورت تصادفی از بیتهای ۰ و ۱ تشکیل شده است.
- mutation_rate احتمال جهش هر ژنوم فرد را مشخص میکند.
- حلقه for خارجی برای ۱۰ نسل ادامه دارد. در هر نسل این فرایندها انجام میشود:
- fitnesses برای هر فرد در جمعیت، براساس تابع برازش (fitness) میزان برازندگیاش محاسبه میشود که نشاندهنده تعداد بیتهای ۱ در ژنوم آن فرد است. فهرست nextgen_population برای ذخیره جمعیت نسل بعد ایجاد میشود. در حلقه داخلی نیمی از جمعیت انتخاب میشوند تا والدین دو فرزند جدید در هر دور باشند. با تابع selection، دو والد از جمعیت فعلی انتخاب میشوند. با تابع crossover فرزندان جدید ازطریق تلاقی (تبادل بخشهایی از ژنوم) میان دو والد تولید میشوند. با تابع mutation به فرزندان جهش اعمال میشود تا تنوع ژنتیکی در جمعیت حفظ شود. این تنوع میتواند کمک کند تا الگوریتم در دام مینیممهای محلی نیفتد و شانس یافتن راهحلهای بهتر را افزایش دهد.
- در پایان هر دوره، جمعیت نسل جدید جایگزین جمعیت فعلی میشود تا فرایند تکامل ادامه یابد.
- این فرایند تکرار میشود و هر نسل جدید با امید به بهبود تناسب کلی جمعیت تولید میشود. از آنجا که تابع تناسب براساس تعداد یکها در ژنوم هر فرد تعریف شده هدف الگوریتم یافتن فردی است که بیشترین تعداد یک را داشته باشد. این نشاندهنده بهینهترین راهحل در مسئله مدنظر است.
خروجی این کد را میتوانید در این شکل ببینید:
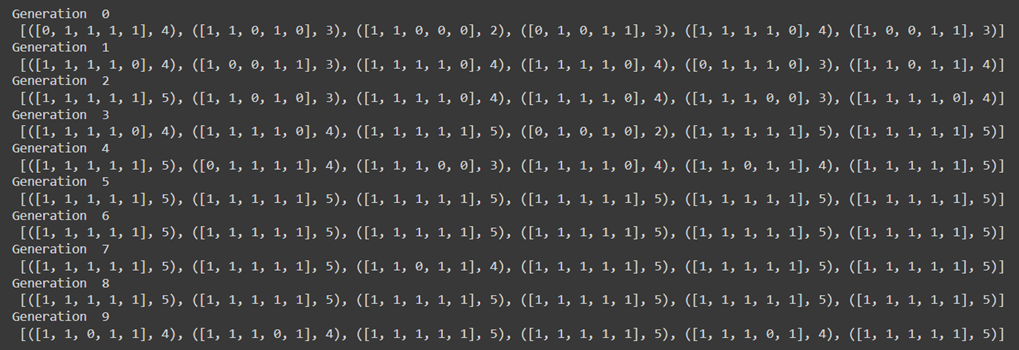
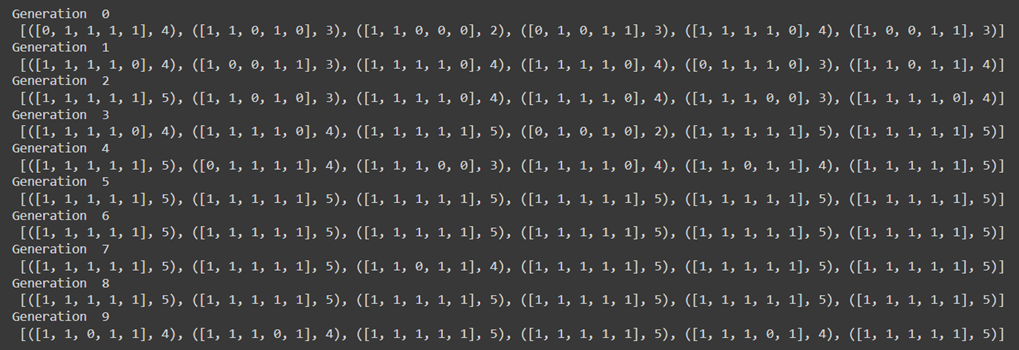
همانطور که در شکل میبینید، بهطور کلی، میزان برازندگی (خروجی تابع برازندگی) نسلهای جدیدتر بیشتر از نسلهای قدیمی است. این نشاندهنده بهبود هر نسل در مقایسه با نسل قبلی است.
تعریف مسئله کولهپشتی ۰ و ۱
مسئله کولهپشتی ۰ و ۱ (0/1Knapsack Problem) یکی از مشهورترین مسئلههای طراحی الگوریتم در زمینه بهینهسازی است. این مسئله بهاین صورت است که شما یک کولهپشتی دارید با ظرفیت وزنی محدود و تعدادی شیء با وزن و ارزش معین.
هدف این است که تا جایی که میشود ارزشمندترین اشیا را در کولهپشتی جای دهید بدون آنکه مجموع وزن آنها از ظرفیت کولهپشتی بیشتر شود. در این مسئله، هر شیء فقط دو حالت دارد: یا باید کاملاً در کولهپشتی قرار بگیرد (یعنی انتخاب شود) یا اصلاً در آن قرار نگیرد (یعنی رد شود). دقت کنید که در این مسئله باید ضمن درنظرگرفتن حداکثر ظرفیت کولهپشتی برای قراردادن اشیا سعی کنیم مجموع ارزش اشیای انتخابشده بیشینه شود.


برای آشنایی مطالعه بیشتر مطلب طراحی الگوریتم کامپیوتر و ویژگیها و کاربردهایش را بخوانید.
حل مسئله کولهپشتی ۰ و ۱ با استفاده از الگوریتم ژنتیک
در این قسمت میخواهیم مسئله کولهپشتی ۰ و ۱ را برای کولهپشتیای با ظرفیت ۵۰ و تعداد ۲۰ شیء که هر یک وزن و قیمت خود را دارند حل کنیم.
برای حل مسئله کولهپشتی (Knapsack Problem) با استفاده از الگوریتم ژنتیک باید تغییراتی در کد قبلی اعمال کنیم. این تغییرات تعریف تابع تناسب جدیدی را شامل است که براساس وزن و ارزش اشیا در کولهپشتی محاسبه میشود؛ همچنین نمایش ژنتیکی هر فرد (کروموزوم) باید بهگونهای باشد که حضورداشتن یا حضورنداشتن هر شیء در کولهپشتی را نشان دهد.
تعریف متغیرها و دادههای اولیه
فرض کنید اشیایی با وزنها و ارزشهای مشخص داریم. این دادهها را در فهرستی از تاپلها (tuples) بهاین شکل تعریف میکنیم. هر tuple وزن و ارزش شیء را شامل است:


تابع مقداردهی اولیه جمعیت
این تابع را مانند قسمت قبل تعریف میکنیم. درواقع هر فرد در جمعیت با یک کروموزوم نمایش داده شده است که بیتهای ۰ یا ۱ را در بر میگیرد. هر بیت نشاندهنده حضورداشتن (۱) یا حضورنداشتن (۰) شیء مربوط در کولهپشتی است:


تابع محاسبه برازندگی
این تابع یکی از قسمتهایی است که باید متناسب با مسئله کولهپشتی تعریف شود. تابع برازندگی ارزش کلی کروموزومها (افراد) را با درنظرگرفتن محدودیت ظرفیت کولهپشتی محاسبه میکند. اگر وزن کل بیش از ظرفیت کولهپشتی باشد، برازش آن فرد را صفر در نظر گرفته میگیریم:
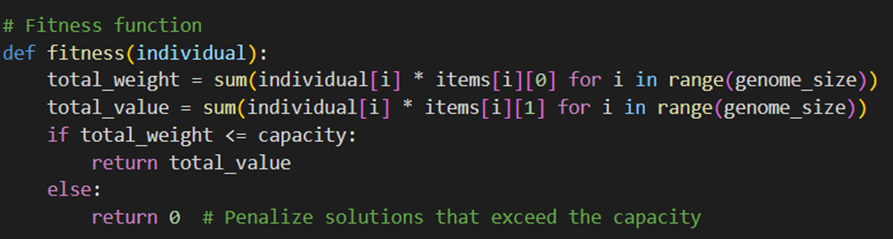

تابع انتخاب
این تابع نیز یکی از توابع تکراری و مشابه قسمت قبل است. در این تابع از روش تورنمنت برای انتخاب والدین استفاده میکنیم. سه فرد را بهصورت تصادفی انتخاب و بهترین فرد (با بالاترین برازش) بهعنوان والد انتخاب میکنیم:
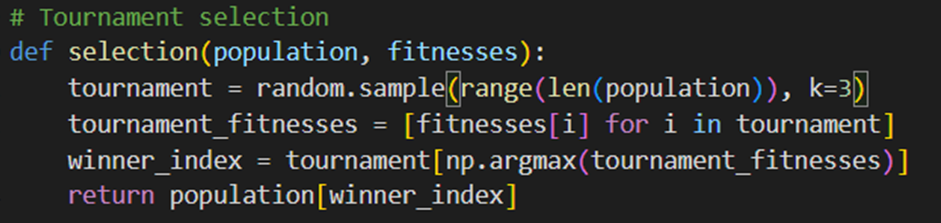

تابع تلاقی
این تابع دو والد را در یک نقطه تصادفی تقسیم و بخشهای آنها را با یکدیگر جابهجا میکند تا دو فرزند جدید تولید شود. تابع تلاقی را نیز مانند کد قبلی بهاین شکل تعریف میکنیم:


تابع جهش
در این تابع انتخاب هر شیء با احتمال مشخصی (بهاندازه rate) تغییر میکند. این تابع را هم مانند قسمت پیش مینویسیم:


تابع الگوریتم ژنتیک برای مسئله کولهپشتی
برای استفاده از الگوریتم ژنتیک در حل مسئله کولهپشتی لازم است در بخش پایانی کد قبل تغییراتی به وجود بیاوریم، هرچند کلیت کد و توصیحاتش همان است.
در این بخش یک تابع genetic_algorithm میسازیم. از این تابع برای مدیریت چرخههای تکرار الگوریتم ژنتیکی استفاده میکنیم:
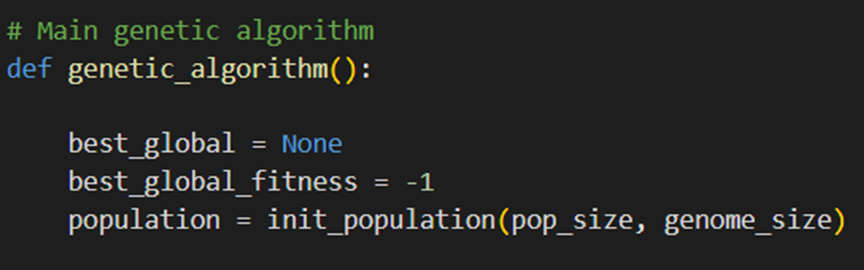

در این تابع:
- best_global بهترین راهحل کلی که تابهحال یافت شده است.
- best_global_fitness برازندگی بهترین راهحل کلی (fitness) که تا به حال یافت شده است.
- مانند کد قبل، جمعیت اولیه با استفاده از تابع init_population ایجاد میشود.
در ادامه یک حلقه for برای تعداد مشخصی نسل (generations) تکرار میشود. در هر تکرار برازش (fitness values) تمام افراد جمعیت محاسبه میشود:
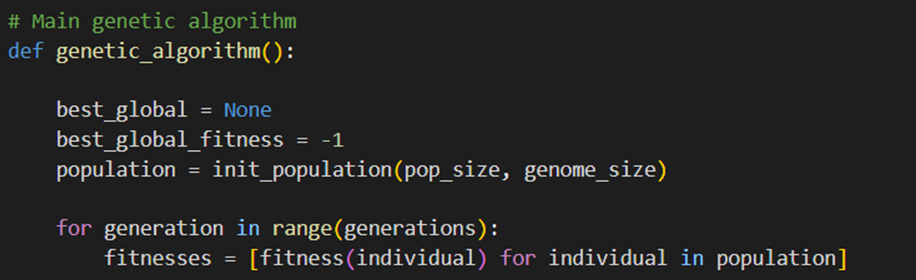

تفاوت این قسمت با کد قبل اینجا به وجود میآید که قبل از ایجاد نسل جدید بررسی میکنیم که آیا راهحل بهتری در جمعیت فعلی وجود دارد که بهتر از best_global_fitness باشد. اگر چنین راهحلی وجود داشته باشد، best_global و best_global_fitness را بهروزرسانی میکنیم:
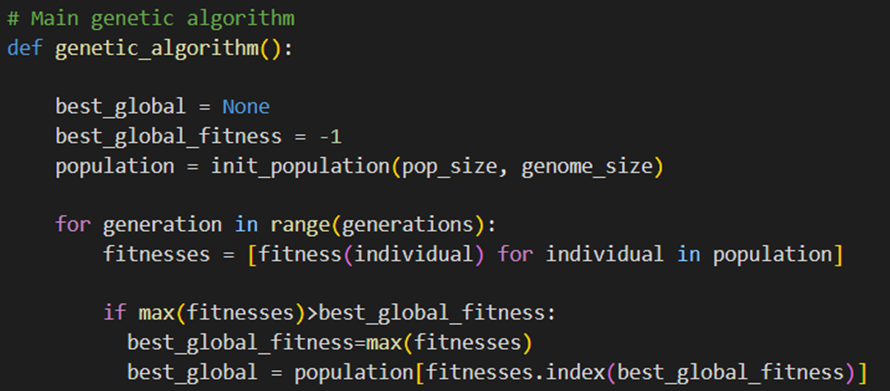

دیگر قسمتها از کد قبلیمان متفاوت نیست و به توضیح نیاز ندارد:
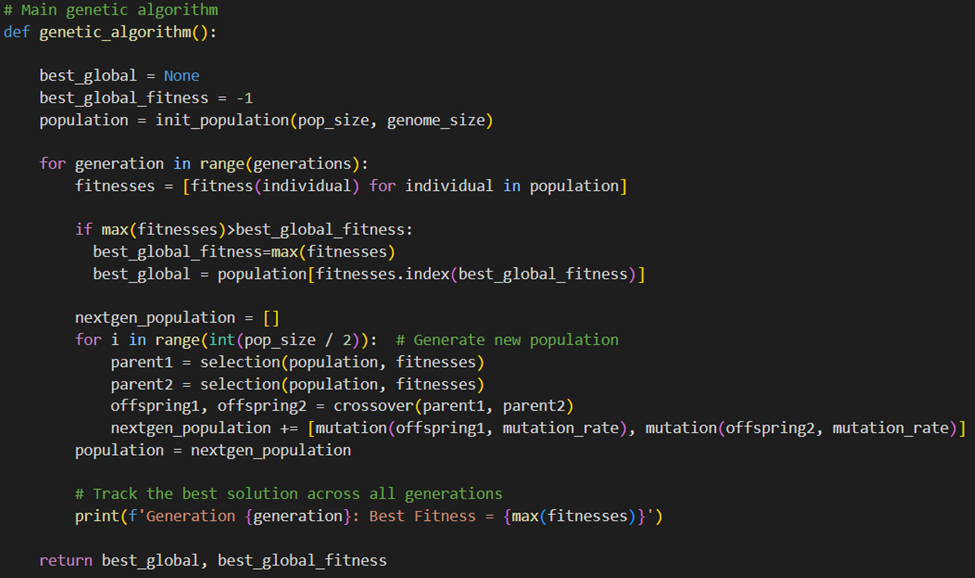

همانطور که قبلا گفتیم، هر فرد با فهرست از ژنها تعریف میشود که در این مسئله نشاندهنده انتخابشدن یا انتخابنشدن هر یک از اشیاست. در پایان، از هر نسل بهترین فرد با بیشترین برازش را چاپ میکنیم.
اجرا و چاپ بهترین راهحل
در این بخش از کد پارامترهای لازم را مقداردهی اولیه و الگوریتم ژنتیک را اجرا میکنیم. سپس بهترین راهحل بهدستآمده را بههمراه میزان برازندگی آن چاپ میکنیم:
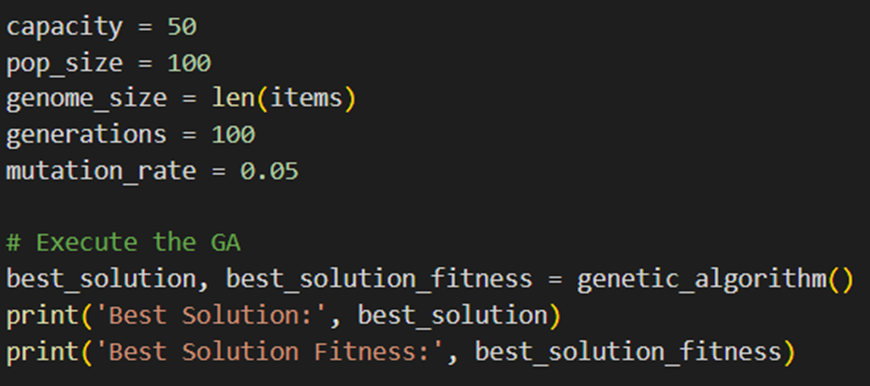

همانطور که مشخص است اندازه جمعیت ۱۰۰ و تعداد نسلها را نیز ۱۰۰ تا در نظر گرفتهایم. احتمال جهش هر ژن نیز ۵ درصد است. خروجی این قطعه کد بهاین صورت در میآید. بهعلت زیادبودن تعداد نسلها (۱۰۰) خروجی را در ۳ شکل جدا نمایش دادهایم:
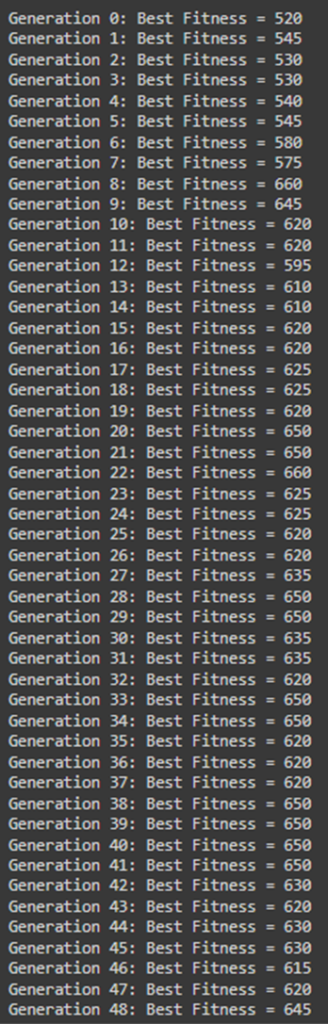

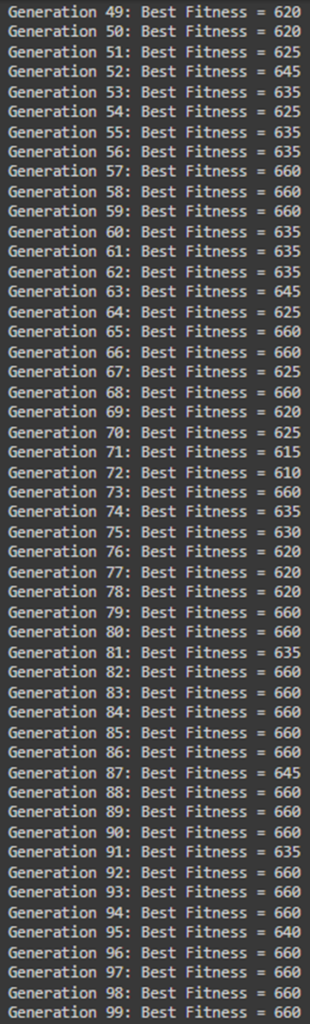



آرایه Best Solution نشاندهنده حضورداشتن یا حضورنداشتن هر شیء در کولهپشتی بهینه است. هر عنصر از این آرایه که یک باشد، نشاندهنده این است که شیء مربوط در کولهپشتی قرار دارد و هر عنصر که صفر باشد، نشاندهنده انتخابنشدن آن شیء است؛ برای مثال، در این فهرست اشیای چهارم، پنجم، ششم، هفتم، دهم، چهاردهم، پانزدهم، شانزدهم، هفدهم و هجدهم در کولهپشتی قرار گرفتهاند که حالت بهینه حل مسئله با اشیای دادهشده است.
Best Solution Fitness نشاندهنده ارزش کل اشیایی است که در کولهپشتی قرار گرفتهاند. درواقع تابع برازندگی که تعریف کردیم، ارزش کل اشیای داخل کولهپشتی را محاسبه میکند، بهشرطی که وزن کل آنها از ظرفیت کولهپشتی تجاوز نکند.


این خروجی نشاندهنده کارایی بالای الگوریتم ژنتیک در یافتن راهحلهای بهینه برای مسائل پیچیده، مانند مسئله کولهپشتی، است که در آن تعادل میان وزن و ارزش اشیا بسیار مهم است.
بررسی صحت جواب الگوریتم ژنتیک با استفاده از برنامهنویسی پویا
در این بخش میخواهیم درستی پاسخ بهدستآمده از روش الگوریتم ژنتیک را با یک قطعه کد بررسی کنیم.
تعریف تابع knapSack
برای این منظور یک تابع بهاین شکل مینویسیم:


این تابع چهار ورودی میگیرد:
- capacity ظرفیت کولهپشتی که نشاندهنده حداکثر وزنی است که کولهپشتی میتواند تحمل کند
- weights فهرست وزنهای اشیای مختلف
- values فهرست ارزشهای اشیای مختلف
- n تعداد اشیا
ایجاد فهرستی از تاپلها
در خط اول فهرستی از تاپلها ایجاد میکنیم:


هر تاپل شامل یک عدد صفر (بهمعنای ارزش اولیه) و یک فهرست خالی (بهمعنای اینکه هنوز هیچ شیئی انتخاب نشده) است. این فهرست برای ذخیره بهترین ارزش ممکن برای هر ظرفیت از 0 تاcapacity استفاده میشود.
حلقههای تکرار برای پرکردن فهرست dp
در ادامه از دو حلقه for تودرتو بهاین صورت اضافه میکنیم:
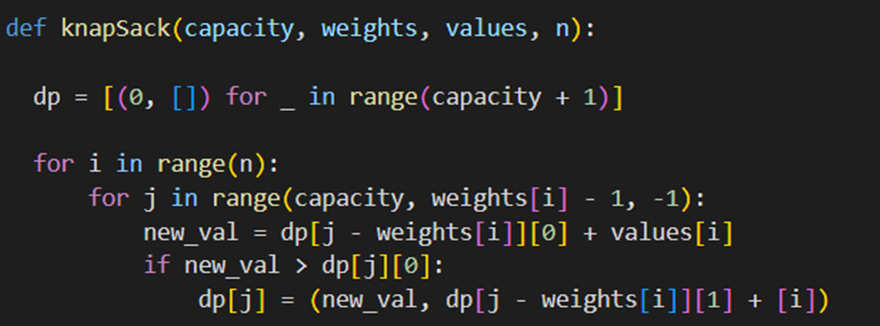

این دو حلقه برای بررسی تمامی اشیا و تمامی ظرفیتهای ممکن است. برای هر شیء از بیشترین ظرفیت شروع میکنیم و به عقب بازمیگردیم تا از تداخل جلوگیری کنیم. اگر اضافهکردن شیء جدید ارزش بیشتری ایجاد کند، آن را در فهرست dp بهروزرسانی میکنیم.
بازگرداندن نتیجه نهایی
پس از پرکردن فهرست dp، بیشترین ارزش و فهرست اشیای انتخابشده برای ظرفیت کامل کولهپشتی را برمیگردانیم و تابع ما کامل میشود:
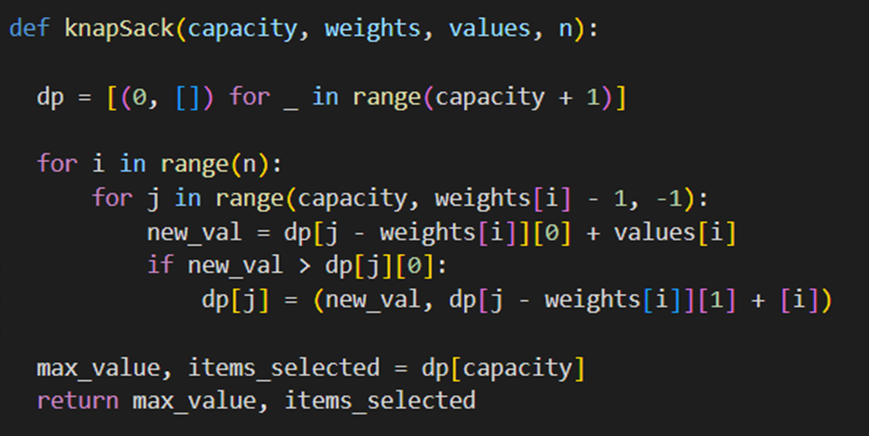

تعریف وزنها و ارزشها
با استفاده از کد زیر فهرست وزنها و ارزشها را از یک فهرست دادهها استخراج میکنیم و سپس تابع knapSack را با ظرفیت ۵۰ فراخوانی میکنیم:


چاپ نتایج
با این خطوط یک آرایه از اعداد صفر ایجاد میکنیم که نشاندهنده اشیای انتخابنشده است. برای هر شیء انتخابشده مقدار متناظر در آرایه به ۱ تغییر میدهیم؛ سپس وزن کل و اشیای انتخابشده را چاپ میکنیم:
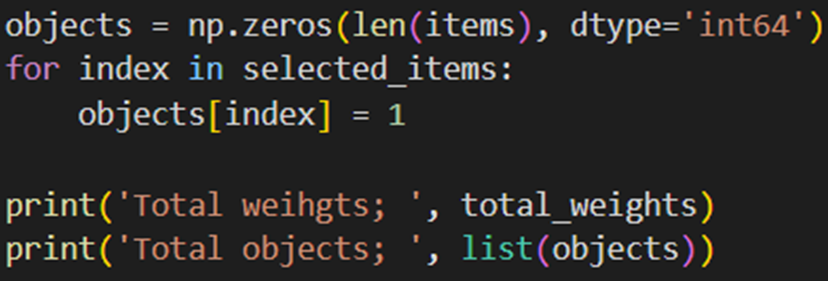

خروجی بهاین شکل درمیآید و میبینیم که با نتیجه حاصل از الگوریتم ژنتیک یکسان است:


چالشها و محدودیتهای الگوریتم ژنتیک در پایتون
- انتخاب اولیه: انتخاب نامناسب اولیه میتواند بر کیفیت نهایی جواب تأثیر منفی داشته باشد و به این بینجامد که الگوریتم به جوابهای خوب دست نیابد.
- حساسیت به پارامترها: تنظیم نادرست پارامترهای الگوریتم، مانند نرخ جهش و اندازه جمعیت، میتواند تأثیر بسزایی بر کارایی و دقت الگوریتم داشته باشد.
- تنوع ژنتیکی: در طول اجرای الگوریتم ممکن است تنوع ژنتیکی در جمعیت کاهش یابد که این امر به کاهش قابلیت اکتشاف الگوریتم و افزایش خطر گیرافتادن در بهینههای محلی میانجامد.
خلاصه مطلب
الگوریتم ژنتیک، با وجود چالشها و محدودیتهایی که دارد، یک ابزار قدرتمند و مؤثر برای حل مسئلههای بهینهسازی پیچیده است. در این مقاله مفاهیم کلیدی مانند ژنوم، کروموزومها، تابع هدف و برازش، جهش، تلاقی و انتخاب را بهدقت بررسی و الگوریتم ژنتیک را با استفاده از زبان برنامهنویسی پایتون پیادهسازی کردیم. سپس با استفاده از آن، مسئله معروف کولهپشتی ۰ و ۱ را نیز حل کردیم.
بهطور کلی، الگوریتم ژنتیک در پایتون بهعنوان یک روش بهینهسازی مؤثر توانسته است در عرصههای متفاوتی ازجمله علم داده، مهندسی و برنامهنویسی نتایج چشمگیری را ارائه کند و بهصورت مداوم در حال توسعه و بهبود است.


سوالات متداول
الگوریتم ژنتیک در پایتون چگونه در مسائل بهینهسازی استفاده میشود؟
الگوریتم ژنتیک با الهام از تکامل طبیعی به حل مسائل پیچیده بهینهسازی (Optimization Problems) میپردازند. در این روش جوابها به صورت کروموزومهایی از ژنها تعریف میشوند که هر ژن نماینده یک ویژگی از راهحل است. این الگوریتمها از عملیاتهای جهش، تلاقی و انتخاب برای تولید نسلهای جدید با ویژگیهای مطلوبتر استفاده میکنند. این فرایند تا رسیدن به شرایط خاتمه مدنظر ادامه مییابد.
چه فرایندهایی در الگوریتم ژنتیک وجود دارد و نقش هر یک چیست؟
سه فرایند اصلی در الگوریتم ژنتیک شامل جهش، تلاقی و انتخاب میشوند. جهش تغییرات تصادفی در ژنها را اعمال میکند تا تنوع ژنتیکی (Genetic Diversity) را افزایش دهد. تلاقی دو کروموزوم را ترکیب میکند تا فرزندانی با ویژگیهای مرکب ایجاد کند. انتخاب بهترین افراد را بر اساس میزان برازندگیشان برای حضور در نسل بعدی انتخاب میکند.
چرا الگوریتم ژنتیک در پایتون برای حل مسئله کولهپشتی مناسب است؟
الگوریتم ژنتیک برای حل مسائلی که به یافتن ترکیبهای بهینه از اشیا با محدودیتهای خاص نیاز دارد بسیار مؤثرند. در مسئله کولهپشتی هدف یافتن بهترین ترکیب از اشیاست که بیشترین ارزش را داشته باشد و وزن کل از ظرفیت محدود کولهپشتی تجاوز نکند که الگوریتم ژنتیک با تنظیمات مناسب میتواند بهخوبی این ترکیبها را بیابد.
چگونه میتوان کارایی الگوریتم ژنتیک را در حل مسائل بهینهسازی افزایش داد؟
کارایی الگوریتم ژنتیک را میتوان با تنظیم دقیق پارامترهایی مانند نرخ جهش، اندازه جمعیت (Population Size) و استراتژیهای انتخاب بهینهسازی کرد؛ همچنین استفاده از تکنیکهای پیشرفته مانند نخبهگرایی (Elitism) که بهترین افراد را برای حفظ ویژگیهای خوب نسل به نسل منتقل میکند، میتواند به افزایش کارایی کمک کند.
تأثیر پیشرفتهای فناوری اطلاعات بر الگوریتم ژنتیک چیست؟
با پیشرفت فناوری اطلاعات، دسترسی به منابع محاسباتی قدرتمندتر و افزایش قابلیتهای ذخیرهسازی دادهها، الگوریتم ژنتیک قادر به حل مسائل بزرگتر و پیچیدهتر با دقت بالاتر شده است. این پیشرفتها امکان پیادهسازی الگوریتمهای پیچیدهتر و کاربرد آنها در مقیاسهای وسیعتر را فراهم کرده است.
یادگیری تحلیل داده و ماشین لرنینگ را از امروز شروع کنید!
دنیای دادهها جذاب است و دانستن علم داده، توانایی تحلیل داده یا بازاریابی مبتنی بر داده یا یادگیری ماشین شما را برای فرصتهای شغلی بسیاری مناسب میکند. شما، فارغ از رشته تحصیلی و پیشزمینه شغلیتان، میتوانید یادگیری این دانش را همین امروز شروع کنید و آن را از سطح مقدماتی تا پیشرفته بیاموزید. اگر دوست دارید به این حوزه وارد شوید، پیشنهاد میکنیم با کلیک روی این لینک قدم اول را همین حالا بردارید.
مشاوران کافهتدریس به شما کمک میکنند مسیر یادگیری برای ورود به این حوزه را شروع کنید:

