الگوریتمهای پیمایش گراف (Graph traversal) مانند جستجوی عمق اول (Depth First Search – DFS) و جستجوی سطح اول (Breadth First Search – BFS)، ابزارهایی قدرتمند برای بازدید از تمامی گرهها و یالهای گراف و استخراج اطلاعات مورد نیاز از آنها میباشند. الگوریتم DFS با پیشروی عمقی در شاخههای گراف و بازگشت به عقب برای بررسی مسیرهای دیگر، به یک درخت پوشا دست مییابد که تمامی گرهها را بدون تکرار یالها نمایش میدهد. در مقابل، الگوریتم BFS با پیشروی سطحی، ابتدا تمامی گرههای همسایه را بازدید کرده و سپس به سطوح بعدی میرود. این الگوریتمها در بسیاری از مسائل علمی و عملی کاربرد دارند و درک صحیح آنها میتواند به بهبود عملکرد در تحلیل و حل مسائل گرافی کمک کند. در این مقاله به بررسی این الگوریتمها و نیز کاربردهای گسترده آنها مانند یافتن مولفههای همبند قوی یا تشخیص دو بخشی بودن گراف خواهیم پرداخت.
- 1. گراف چیست؟
- 2. الگوریتمهای پیمایش گراف
-
3.
الگوریتم جستجوی عمق اول
- 3.1. تاریخچه الگوریتم جستجوی عمق اول
- 3.2. خروجی الگوریتم جستجوی عمق اول
- 3.3. الگوریتم جستجوی عمق اول چطور کار میکند؟
- 3.4. بررسی گامبهگام مراحل اجرای الگوریتم جستجوی عمق اول
- 3.5. پیادهسازی الگوریتم جستجوی عمق اول درپایتون
-
3.6.
کاربردهای الگوریتم جستجوی عمق اول
- 3.6.1. تشخیص وجود مسیر
- 3.6.2. چطور با جستجوی عمق اول یک مسیر را در یک گراف پیدا کنیم؟
- 3.6.3. پیادهسازی الگوریتم یافتن مسیر در گراف با جستجوی عمق اول در پایتون
- 3.6.4. تشخیص دو بخشیبودن گراف
- 3.6.5. چطور با جستجوی عمق اول تشخیص دهیم یک گراف دو بخشی است؟
- 3.6.6. پیادهسازی الگوریتم تشخیص دو بخشی بودن گراف با جستجوی عمق اول در پایتون
- 3.6.7. تشخیص دور
- 3.6.8. چطور با جستجوی عمق اول تشخیص دهیم یک گراف دور دارد؟
- 3.6.9. پیادهسازی الگوریتم تشخیص دور در گراف با جستجوی عمق اول در پایتون
- 3.6.10. تشخیص مولفههای قویا همبند گراف
- 3.6.11. چطور با جستجوی عمق اول مولفههای قویا همبند یک گراف را تشخیص دهیم؟
- 3.6.12. پیادهسازی الگوریتم تشخیص مولفههای قویا همبند گراف با جستجوی عمق اول در پایتون
- 3.6.13. مرتبسازی توپولوژیکی
- 3.6.14. چطور با جستجوی عمق اول ترتیب توپولوژیکی یک گراف را پیدا کنیم؟
- 3.6.15. پیادهسازی الگوریتم تشخیص ترتیب توپولوژیکی گراف با جستجوی عمق اول در پایتون
-
4.
الگوریتم جستجوی سطح اول
- 4.1. تاریخچه الگوریتم جستجوی سطح اول
- 4.2. خروجی الگوریتم جستجوی سطح اول
- 4.3. الگوریتم جستجوی سطح اول چطور کار میکند؟
- 4.4. بررسی گامبهگام مراحل اجرای الگوریتم جستجوی سطح اول
- 4.5. پیادهسازی الگوریتم جستجوی سطح اول در پایتون
-
4.6.
کاربردهای الگوریتم جستجوی سطح اول
- 4.6.1. یافتن مسیر در گراف با استفاده از جستجوی سطح اول
- 4.6.2. چطور با جستجوی سطح اول یک مسیر را در یک گراف پیدا کنیم؟
- 4.6.3. پیادهسازی الگوریتم یافتن مسیر در گراف با جستجوی سطح اول در پایتون
- 4.6.4. یافتن کوتاهترین مسیر در گرافهای بیوزن
- 4.6.5. چطور با جستجوی سطح اول کوتاهترین مسیر را در یک گراف بیوزن را پیدا کنیم؟
- 4.6.6. پیادهسازی الگوریتم یافتن کوتاهترین مسیر گراف بیوزن با جستجوی سطح اول در پایتون
- 4.6.7. تشخیص دو بخشی بودن گراف
- 4.6.8. چطور با جستجوی سطح اول تشخیص دهیم یک گراف دو بخشی است؟
- 4.6.9. پیادهسازی الگوریتم تشخیص دو بخشی بودن گراف با جستجوی سطح اول در پایتون
- 5. جمعبندی الگوریتمهای پیمایش گراف
- 6. پیچیدگی زمانی و مکانی الگوریتمها
- 7. مزایا و معایب الگوریتمهای DFS و BFS
- 8. کلام آخر درباره الگوریتمهای پیمایش گراف
-
9.
پرسشهای متداول
- 9.1. الگوریتم جستجوی عمق اول چگونه در یافتن درخت پوشا در گرافها به کار میرود؟
- 9.2. چه تفاوتهایی بین الگوریتمهای پیمایش گراف جستجوی عمق اول و جستجوی سطح اول وجود دارد؟
- 9.3. چگونه میتوان از الگوریتم جستجوی عمق اول برای تشخیص مولفههای قویاً همبند استفاده کرد؟
- 9.4. الگوریتم جستجوی سطح اول چگونه میتواند در یافتن کوتاهترین مسیر در گرافهای بیوزن کمک کند؟
- 9.5. چه کاربردهایی برای الگوریتم جستجوی عمق اول و جستجوی سطح اول در زمینههای عملی مختلف وجود دارد؟
- 10. یادگیری تحلیل داده را از امروز شروع کنید!
گراف چیست؟
گرافها ساختارهای دادهای هستند که از مجموعهای از گرهها (نودها) و یالها (لبهها) تشکیل شدهاند. هر گره میتواند نمایانگر یک نقطه از دادهها و هر یال میتواند نمایانگر ارتباط بین دو گره باشد. گرافها میتوانند جهتدار یا غیرجهتدار باشند. در گرافهای جهتدار، یالها دارای جهت هستند و نشان میدهند که ارتباط از یک گره به گره دیگر به چه صورت است. در گرافهای غیرجهتدار، یالها جهت ندارند و ارتباط بین گرهها دوطرفه است.
برای آشنایی بیشتر با گراف و انواع آن مطالعه مقاله نظریه گراف: پلی بین ریاضیات و دنیای واقعی را پیشنهاد میکنیم.
الگوریتمهای پیمایش گراف
الگوریتمهای پیمایش گراف (Graph traversal) به ما کمک میکنند تا تمامی گرهها و یالهای یک گراف را بازدید کنیم و اطلاعات مورد نیاز را استخراج کنیم. این الگوریتمها پایه و اساس بسیاری از مسائل مهم در علوم کامپیوتر و تحلیل دادهها هستند. با استفاده از این الگوریتمها میتوانیم به درک بهتری از ساختار و ویژگیهای گرافها برسیم و مسائل پیچیدهای مانند جستجوی مسیر، دور و غیره در گرافها را حل کنیم.
الگوریتم جستجوی عمق اول
الگوریتم جستجوی عمق اول (Depth First Search – DFS) یکی از الگوریتمهای پیمایش گراف پایهای برای گرافها و درختها است. در این الگوریتم، جستجو از یک نقطه شروع میشود و به صورت عمقی به هر شاخه رفته و تا حد ممکن در همان شاخه پیش میرود تا به نقطهای برسد که دیگر امکان پیشروی نباشد، آنگاه به نقاط قبلی بازمیگردد و مسیرهای دیگر را بررسی میکند.
تاریخچه الگوریتم جستجوی عمق اول
الگوریتم جستجوی عمق اول (DFS) یکی از قدیمیترین و پرکاربردترین روشهای جستجو در علوم کامپیوتر است. ریشههای این الگوریتم به سالهای اولیهٔ دههٔ ۱۹۵۰ برمیگردد. نخستین بار، این الگوریتم به صورت ضمنی در پژوهشهای مربوط به نظریه گرافها مطرح شد. جستجوی اول عمق به طور رسمی در سال ۱۹۵۹ توسط یک ریاضیدان به نام ادوارد مور (Edward F. Moore) در دانشگاه پنسیلوانیا معرفی شد. او این روش را به عنوان بخشی از تحقیق خود در زمینهٔ ماشینهای متناهی و نظریهٔ زبانهای رسمی مطرح کرد.
پس از معرفی اولیه، الگوریتم DFS به سرعت توجه دانشمندان علوم کامپیوتر را به خود جلب کرد. در دههٔ ۱۹۷۰، پژوهشگران بیشتری به توسعه و بهبود این الگوریتم پرداختند. رابرت تارچن (Robert Tarjan) یکی از افراد برجستهای بود که در این زمینه فعالیت کرد. او در سال ۱۹۷۲ از این الگوریتم برای حل مسائل مختلفی نظیر یافتن مولفههای قویا همبند در گرافها استفاده کرد. نتایج کارهای تارچن باعث شد تا DFS به عنوان یک ابزار قدرتمند در تحلیل و حل مسائل گرافی شناخته شود.
خروجی الگوریتم جستجوی عمق اول
هنگامی که الگوریتم جستجوی عمق اول یا همان DFS از یک گره شروع به کار میکند و به صورت بازگشتی به تمامی گرههای قابل دسترس در گراف میرود، مسیری از گرهها و یالها تشکیل میشود که یک درخت پوشا (Spanning Tree) است. این درخت پوشا شامل تمامی گرههای گراف میشود و حداقل تعداد یالها را دارد به طوری که تمام گرهها به هم متصل باشند و هیچ حلقهای در گراف ایجاد نشود. به عبارتی دیگر، خروجی DFS میتواند به عنوان یک درخت پوشا در نظر گرفته شود که مسیرهای پیمایش شده در گراف را بدون تکرار یالها و ایجاد چرخه نمایش میدهد.
الگوریتم جستجوی عمق اول چطور کار میکند؟
الگوریتم DFS از یک گره شروع میکند که به عنوان گره آغازین انتخاب میشود. این گره میتواند هر گرهای از گراف باشد (پس خروجی الگوریتم DFS منحصربهفرد نیست). در بیشتر پیادهسازیها، این گره به عنوان گره «ریشه» یا گره «مبدا» شناخته میشود. از گره مبدا، به یکی از گرههای همسایه پیش میرویم. این فرایند تا زمانی ادامه پیدا میکند که به یک گره برسیم که هیچ همسایهای نداشته باشد که هنوز بازدید نشده باشد. این به معنای پیشروی به عمق گراف است. زمانی که به گرهی میرسیم که هیچ همسایهای ندارد که هنوز بازدید نشده باشد، به گره قبلی بازمیگردیم و دیگر همسایههای آن را بررسی میکنیم. این فرایند بازگشت به عقب (Back tracking) نامیده میشود. گرههای پیمایش شده را علامتگذاری میکنیم تا از بازدید مجدد آنها جلوگیری شود. این علامتگذاری میتواند با استفاده از یک مجموعه یا لیست (اغلب به نام visited) انجام شود.


بررسی گامبهگام مراحل اجرای الگوریتم جستجوی عمق اول
حال بیایید کمی عمیقتر روند اجرای الگوریتم DFS را مرور کنیم. برای این منظور فرض کنید یک گراف بهشکل زیر داریم:


گسترش گره
برای اجرای الگوریتم DFS نیاز به یک پشته (stack) و یک لیست بهنام visited برای علامتگذاری گرهها بهعنوان ملاقاتشده داریم. در گام نخست یک گره دلخواه را انتخاب کرده (مثلا گره صفر) و آن را در پشته قرار میدهیم (stack.push). سپس چون گره دیگری در پشته نیست، همین گره را گسترش میدهیم، بهاین معنی که آن را از پشته خارج (stack.pop) و – درصورتی که تاکنون ملاقات نشده – بهعنوان ملاقات شده علامتگذاری میکنیم.
پردازش گره و تولید همسایههای آن
اکنون میتوانیم گره را پردازش کنیم. عمل پردازش میتواند هرچیزی باشد، مثلا چاپ نام گره یا هر عملیات دیگری که مد نظر ما است. حال باید همسایههایی از گره صفر را که ملاقات نشدهاند، تولید کنیم. دراینجا تولید کردن بهاین معنی است که آنها را در پشته قرار دهیم:
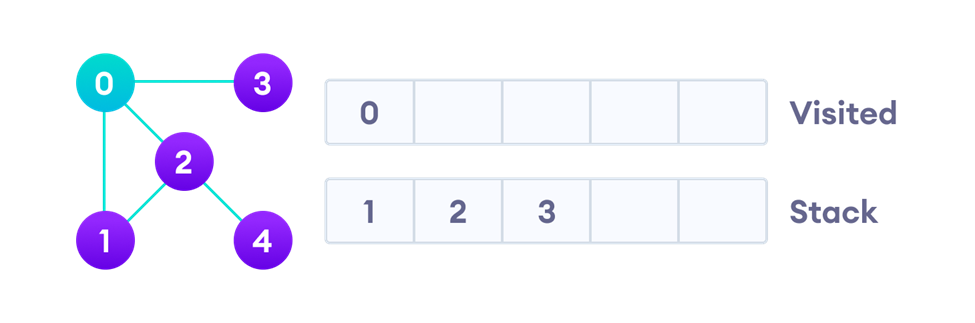

تکرار مراحل بالا برای سایر گرهها
اکنون باید همسایهای از گره صفر که در بالاترین قسمت پشته (سمت چپ) قرار دارد را گسترش دهیم، یعنی گره یک. همانطور که گفتیم، گسترش یعنی گره را از پشته خارج و سپس اگر تابهحال ملاقات نشده، آن را در لیست ملاقاتشدهها قرار دهیم:
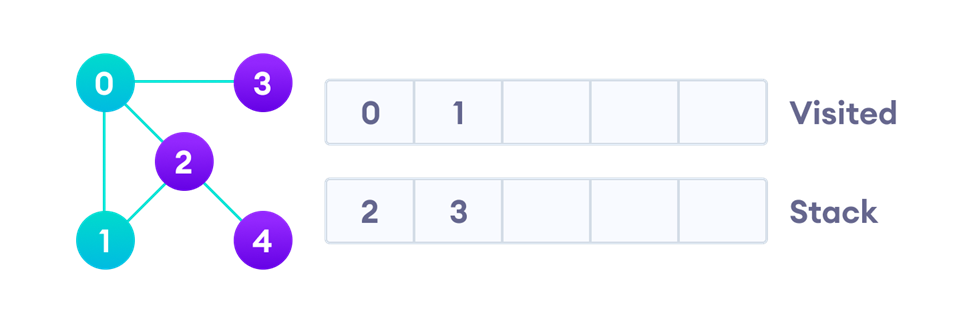

در مرحله بعد باید گره یک را پردازش کرده و همسایههای از آن را که هنوز ملاقات نشدهاند، در پشته قرار دهیم. همسایههای گره یک گرههای صفر و دو هستند که از بین آنها صفر ملاقاتشده و دو هم قبلا در پشته قرار گرفته است، بههمین درشکل بالا دلیل دوباره آن را در پشته قرار نمیدهیم. البته بعدا در پیادهسازی کد این الگوریتم نشان خواهیم داد که درچنین شرایطی واقعا گره دو مجددا وارد پشته میشود (چون هنوز ملاقات نشده) اما این موضوع روند اجرای الگوریتم را با مشکل روبهرو نمیکند چون پیش از آنکه دوباره آن را پردازش کنیم، بررسی میکنیم که در لیست ملاقاتشدهها هست یا خیر و اگر قبلا یک بار بهعنوان ملاقاتشده علامتگذاری شده باشد، دوباره پردازش نمیشود.
اکنون سراغ گره شماره دو که در بالای پشته قرار دارد میرویم و آن را گسترش میدهیم. بهاینترتیب از پشته خارج شده و در لیست ملاقاتشدهها قرار میگیرد. بعد از پردازش، همسایههایی از گره دو را که هنوز ملاقاتنشدهاند (یعنی فقط گره چهار) در بالای پشته قرار میدهیم:
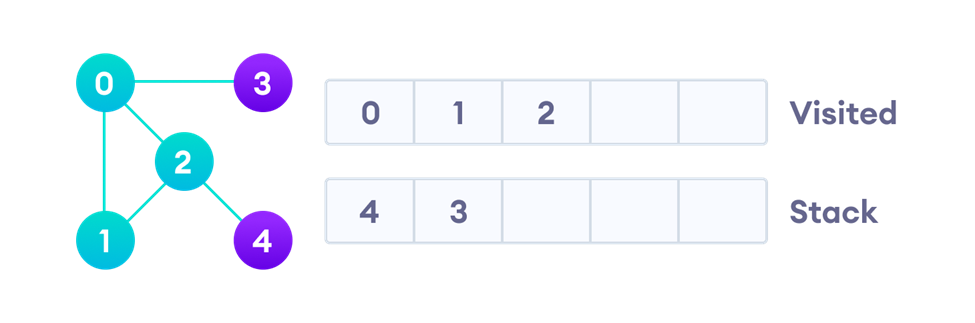

در قسمت بعد گره چهار را که در بالای پشته است، گسترش میدهیم. بهاینترتیب گره چهار در لیست ملاقاتشدهها قرار میگیرد و چون تنها همسایهاش (یعنی گره دو) قبلا بهعنوان ملاقاتشده علامت خورده، کار دیگری انجام نمیشود:
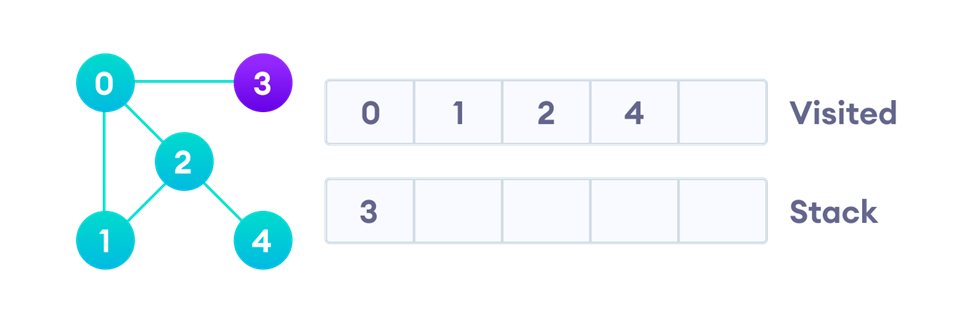

حال تنها گره سه باقیمانده است. این گره نیز گسترش یافته و از پشته خارج میشود. سپس در لیست ملاقاتشدهها قرار میگیرد و چون تنها همسایهاش که گره یک است نیز قبلا ملاقات شده، کار دیگری انجام نمیشود:
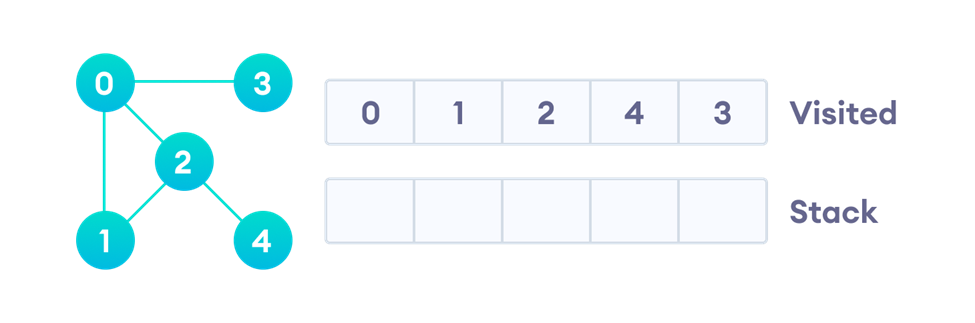

با خالی شدن پشته، الگوریتم جستجوی عمق اول به پایان میرسد.
پیادهسازی الگوریتم جستجوی عمق اول درپایتون
پیادهسازی الگوریتم DFS به عنوان یکی از الگوریتمهای پیمایش گراف میتواند به صورت بازگشتی یا غیربازگشتی انجام شود. در روش بازگشتی، از فراخوانی توابع استفاده میشود، درحالیکه در روش غیربازگشتی، از یک ساختار دادهای پشته بهصورت صریح استفاده میشود.
پیادهسازی الگوریتم جستجوی عمق اول به صورت غیربازگشتی
در ادامه، الگوریتم جستجوی عمق اول را بهصورت غیربازگشتی، با استفاده از زبان برنامهنویسی پایتون و گرافی که در بالا آن را بهعنوان نمونه بررسی کردیم، پیادهسازی خواهیم کرد. این مثال به شما کمک میکند تا با فرآیند این الگوریتم بهخوبی آشنا شوید و بتوانید آن را درمسائل مختلف بهکار بگیرید.
برای این منظور ابتدا یک تابع به نام dfs_iterative تعریف میکنیم که گراف مورد نظر و گره شروع (یک گره دلخواه) را به عنوان ورودی دریافت میکند. در ابتدای این تابع یک لیست بهنام visited تعریف میکنیم که همانطور که توضیح دادیم، نقش ذخیره گرههای بازدیدشده را دارد. لیست دیگری بهعنوان پشته به نام stack نیز تعریف میکنیم که بعد از تولید همسایههای گره جاری، آنها در آن قرار دهیم. سپس در یک حلقه while که تا خالیشدن کامل پشته برقرار خواهد بود، گره جاری را گسترش میدهیم. یعنی آن را از پشته pop کرده و در صورتی که تاکنون ملاقات نشده، آن را به لیست ملاقاتشدهها اضافه میکنیم. اکنون میتوان گره ملاقاتشده را پردازش کرد. ما در اینجا برای سادگی عمل پردازش را چاپ (print) گره تعریف میکنیم. در پایان نیز همسایههای ملاقاتنشده گره را به پشته اضافه میکنیم:
def dfs_iterative(graph, start):
# a list to store visited nodes
visited = []
# put the initial node in the stack
stack = [start]
# repeat until the stack is empty
while stack:
# extend the node
node = stack.pop()
# check if the node is not visited
if node not in visited:
# mark the node as visited
visited.append(node)
print(f'Process node: {node}') # or any other process
# produce nodes
stack.extend(sorted([n for n in graph[node] if n not in visited], reverse=True))
print(f'Stack: {stack}, Visited: {visited}\n')
ما برای سادگی کار و تمرکز روی توضیح کد اصلی برای تعریف گراف از یک دیکشنری استفاده میکنیم اما راه بهتر و اصولی آن است که گراف خود را با توجه به دستوراتی که در مقاله معرفی جامع روشهای نمایش گراف برای ساخت یک گراف در کامیپوتر توضیح دادیم، تعریف کنیم. خروجی کد بالا روی گراف طراحیشده بهصورت زیر است:
# Define the graph with nodes
graph = {
0: [1, 2, 3],
1: [0, 2],
2: [0, 1, 4],
3: [0],
4: [2]
}
dfs_iterative(graph, 0)
Process node: 0
Stack: [3, 2, 1], Visited: [0]
Process node: 1
Stack: [3, 2, 2], Visited: [0, 1]
Process node: 2
Stack: [3, 2, 4], Visited: [0, 1, 2]
Process node: 4
Stack: [3, 2], Visited: [0, 1, 2, 4]
Process node: 3
Stack: [], Visited: [0, 1, 2, 4, 3]
بررسی خروجی الگوریتم جستجوی عمق اول به صورت غیربازگشتی
همانطور که در خروجی این کد میبینید، روندی که در قسمت قبل روی شکل آن را توضیح دادیم در این قسمت نیز اجرا شده است.
نکته قابل توجه ورود دوباره گره دو به پشته است اما چون پیش از پردازش هر گره خارجشده از پشته، ابتدا حضورش در لیست ملاقاتشدهها را بررسی میکنیم، با اینکه بعد از پردازش گره چهار (خط چهارم خروجی) انتظار داریم مجددا گره شماره دو پردازش شود، این اتفاق نمیافتد و این گره فقط از پشته خارج میشود.
پیادهسازی الگوریتم جستجوی عمق اول به صورت بازگشتی
توضیحات مربوط به اجرای الگوریتم جستجوی عمق اول به صورت بازگشتی نیز تقریبا مشابه حالت غیربازگشتی است با این تفاوت که بهجای پشته از فراخوانی مجدد تابع استفاده میکند. همانطور که مشخص است، خروجی الگوریتم DFS در این حالت نیز طبق انتظار مشابه حالت غیربازگشتی است (توجه کنید که منظور از خروجی ترتیب پردازش گرهها است و چاپ پشته و لیست ملاقاتشدهها درقسمت الگوریتم غیربازگشتی صرفا برای درک بهتر روند اجرای الگوریتم بود):
def dfs_recursive(graph, start, visited=None):
# a list to store visited nodes
if visited is None:
visited = []
# mark the node as visited
visited.append(start)
print(f'Process node: {start}') # or any other process
# recursively visit all the unvisited neighbors of the current node
for neighbor in graph[start]:
if neighbor not in visited:
dfs_recursive(graph, neighbor, visited)
برای مشاهده خروجی کد بالا به صورت زیر عمل میکنیم:
# Define the graph with nodes
graph = {
0: [1, 2, 3],
1: [0, 2],
2: [0, 1, 4],
3: [0],
4: [2]
}
dfs_recursive(graph, 0)
Process node: 0
Process node: 1
Process node: 2
Process node: 4
Process node: 3
کاربردهای الگوریتم جستجوی عمق اول
الگوریتم جستجوی عمق اول یا DFS یکی از الگوریتمهای پایهای در نظریه گرافها و علوم کامپیوتر است. این الگوریتم کاربردهای زیادی دارد که به برخی از مهمترین آنها اشاره میکنیم:
تشخیص وجود مسیر
یکی از کاربردهای الگوریتم DFS، یافتن یک مسیر از یک گره به گره دیگر در یک گراف است. DFS گرهها را به ترتیب عمق بازدید میکند تا به گره هدف برسد. این روش در مسائلی که نیاز به بررسی همه مسیرهای ممکن از یک نقطه شروع تا یک نقطه هدف داریم، مفید است.
چطور با جستجوی عمق اول یک مسیر را در یک گراف پیدا کنیم؟
برای یافتن یک مسیر در یک گراف با استفاده از جستجوی عمق اول همان الگوریتم اصلی DFS را اجرا میکنیم. در این حالت، پردازش گره به معنای بررسی هدف بودن آن گره است و شرط توقف الگوریتم، رسیدن به گره هدف یا خالی شدن پشته است.
پیادهسازی الگوریتم یافتن مسیر در گراف با جستجوی عمق اول در پایتون
برای پیادهسازی الگوریتم یافتن مسیر در یک گراف با استفاده از جستجوی عمق اول از تابع dfs_search استفاده میکنیم. در این تابع، از یک پشته برای نگهداری گرهها استفاده میکنیم. گره شروع را به پشته اضافه میکنیم و سپس گرهها را از پشته خارج کرده و همسایههای آنها را به پشته اضافه میکنیم. اگر در طی این بازدید به گره هدف برسیم، جستجو متوقف میشود و True برگردانده میشود. در غیر این صورت، جستجو ادامه مییابد تا زمانی که پشته خالی شود و در این صورت False برگردانده میشود:
def dfs_search(graph, start, target):
# a list to store visited nodes
visited = []
# put the initial node in the stack
stack = [start]
while stack:
# extend the node
node = stack.pop()
# process the node
if node == target:
return True
# check if the node is not visited
if node not in visited:
# mark the node as visited
visited.append(node)
# produce nodes
stack.extend(sorted([n for n in graph[node] if n not in visited], reverse=True))
return False
خروجی کد بالا روی گراف مورد نظر را به صورت زیر میتوان دید:
# Define the graph with nodes
graph = {
0: [1, 2, 3],
1: [0, 2],
2: [0, 1, 4],
3: [0],
4: [2]
}
result = dfs_search(graph, 0, 4)
print("Found target:", result)
Found target: True
تشخیص دو بخشیبودن گراف
یکی دیگر از کاربردهای الگوریتم DFS به عنوان یکی از الگوریتمهای پیمایش گراف تشخیص دو بخشیبودن گراف است. گراف دو بخشی (Bipartite Graph) به گرافی گفته میشود که میتوان گرههای آن را به دو مجموعه مجزا تقسیم کرد به گونهای که هیچ دو گرهای در داخل یک مجموعه به هم متصل نباشند. با استفاده از DFS میتوانیم بررسی کنیم که آیا یک گراف دو بخشی است یا خیر. این کار با تلاش برای رنگآمیزی گراف با دو رنگ و تشخیص اینکه دو گره مجاور رنگ یکسان دارند یا خیر، انجام میشود. این کاربرد در مسائل مختلفی مانند تخصیص منابع و شبکههای ارتباطی مفید است.
برای آشنایی بیشتر با گرافهای دو بخشی، میتوانید مقاله نظریه گراف: پلی بین ریاضیات و دنیای واقعی را بخوانید.
چطور با جستجوی عمق اول تشخیص دهیم یک گراف دو بخشی است؟
برای تشخیص دو بخشی بودن یک گراف، از روش رنگآمیزی استفاده میکنیم. برای این کار گرهها را با دو رنگ متفاوت رنگآمیزی میکنیم به طوری که رنگ هر گره با رنگ همسایههایش متفاوت باشد. اگر در طی فرآیند رنگآمیزی به گرهای رسیدیم که مجبور شدیم آن را همرنگ با یکی از همسایههایش رنگ بزنیم، گراف دو بخشی نیست. در غیر این صورت، گراف دو بخشی است.
پیادهسازی الگوریتم تشخیص دو بخشی بودن گراف با جستجوی عمق اول در پایتون
برای پیادهسازی الگوریتم تشخیص دو بخشی بودن گراف با استفاده از جستجوی عمق اول از دو تابع اصلی dfs_bipartite و is_bipartite استفاده میکنیم. در تابع dfs_bipartite، هر گره را با رنگی (کدشده با ۰ و ۱) مشخص میکنیم و سپس به صورت بازگشتی همسایههای آن گره را با رنگ مخالف بازدید میکنیم. اگر در طی این بازدید به گرهای برسیم که قبلاً بازدید شده و رنگ آن با رنگ فعلی مطابقت داشته باشد (یعنی رنگ یک گره با رنگ همسایهاش یکی شود)، گراف دو بخشی نیست و تابع False برمیگرداند. در غیر این صورت، پس از بازدید از تمامی همسایهها، تابع True برمیگرداند. تابع is_bipartite مجموعهای از گرههای بازدید شده را نگهداری میکند و برای هر گره در گراف، اگر بازدید نشده باشد، تابع dfs_bipartite را با رنگ ابتدایی ۰ فراخوانی میکند. اگر گراف دو بخشی باشد، True برمیگرداند، در غیر این صورت False برمیگرداند:
def dfs_bipartite(graph, node, color, colors, visited):
# color the node
colors[node] = color
# mark the node as visited
visited.append(node)
for neighbor in graph[node]:
if neighbor not in visited:
if not dfs_bipartite(graph, neighbor, 1 - color, colors, visited): # swap color
return False
# if the color doesn't match, the graph is not bipartite
elif colors[neighbor] == color:
return False
return True
def is_bipartite(graph):
# dictionary to store the colors of nodes
colors = {}
# list to store visited nodes
visited = []
# recursively visit all the unvisited nodes of the graph
for node in graph:
if node not in visited:
if not dfs_bipartite(graph, node, 0, colors, visited): # start DFS with color 0
return False
return True
خروجی کد بالا روی گراف زیر را در ادامه میتوانید ببینید:
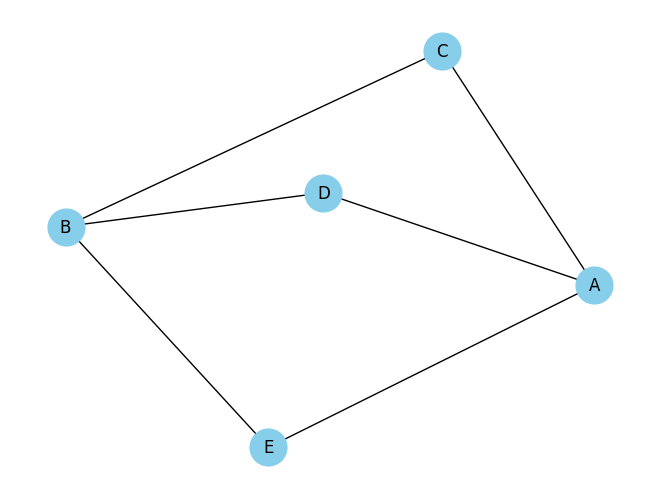

# Define the graph with nodes and edges
graph = {
'A': ['C', 'D', 'E'],
'B': ['C', 'D', 'E'],
'C': ['A', 'B'],
'D': ['A', 'B'],
'E': ['A', 'B']
}
result = is_bipartite(graph)
print("Is the graph bipartite?", result)
Is the graph bipartite? True
تشخیص دور
تشخیص دور (Cycle Detection) در گراف یکی دیگر از کاربردهای مهم الگوریتم جستجوی عمق اول است. این ویژگی به ما کمک میکند تا بررسی کنیم که آیا یک گراف شامل دور است یا خیر. این کاربرد در تحلیل پایداری سیستمها و شبکهها، جلوگیری از حلقههای بینهایت در برنامههای کامپیوتری و تحلیل وابستگیها در پروژهها اهمیت زیادی دارد.
چطور با جستجوی عمق اول تشخیص دهیم یک گراف دور دارد؟
برای تشخیص اینکه یک گراف دارای دور (حلقه) است، میتوان از جستجوی عمق اول (DFS) استفاده کرد. در حین پیمایش DFS، اگر به یک گرهای برسیم که قبلاً بازدید شده و والد فعلی گره نباشد، نشاندهنده وجود دور در گراف است.
پیادهسازی الگوریتم تشخیص دور در گراف با جستجوی عمق اول در پایتون
برای پیادهسازی الگوریتم تشخیص حلقه در گراف با استفاده از جستجوی عمق اول (DFS) از دو تابع اصلی dfs_cycle_detect و has_cycle استفاده میکنیم. در تابع dfs_cycle_detect، از هر گره شروع کرده و به صورت بازگشتی همسایههای آن گره را بازدید میکنیم. اگر در طی این بازدید به گرهای برسیم که قبلاً بازدید شده و والد فعلی گره نباشد، دور در گراف شناسایی میشود و تابع True برمیگرداند. در غیر این صورت، پس از بازدید از تمامی همسایهها، تابع False برمیگرداند. تابع has_cycle مجموعهای از گرههای بازدید شده را نگهداری میکند و برای هر گره در گراف، اگر بازدید نشده باشد، تابع dfs_cycle_detect را فراخوانی میکند. اگر حلقهای در هر یک از این بازدیدها شناسایی شود، True برمیگرداند، در غیر این صورت False برمیگرداند:
def dfs_cycle_detect(graph, node, visited, parent):
# Mark the node as visited
visited.append(node)
# Traverse neighbors
for neighbor in graph[node]:
if neighbor not in visited:
# Recursively visit the neighbor
if dfs_cycle_detect(graph, neighbor, visited, node):
return True
elif parent is not None and neighbor != parent:
# If the neighbor is visited and it is not the parent, a cycle is detected
return True
return False
def has_cycle(graph):
# List to keep track of visited nodes
visited = []
for node in graph:
if node not in visited:
if dfs_cycle_detect(graph, node, visited, None):
return True
return False
خروجی کد بالا روی گراف زیر را در ادامه میتوانید ببینید:
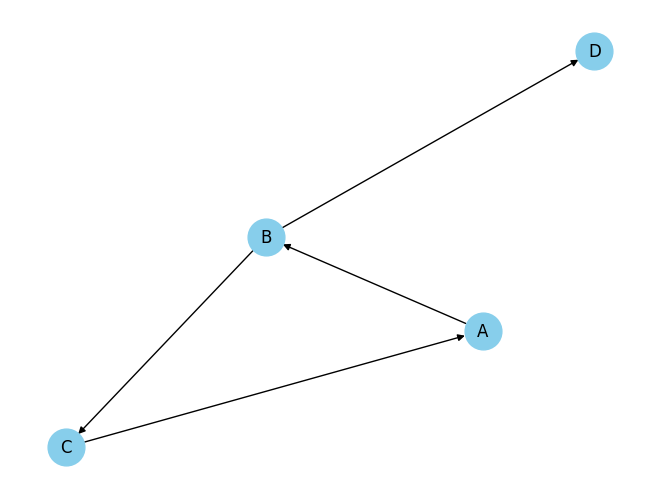

# Define the graph with nodes and directed edges using lists
graph = {
'A': ['B'],
'B': ['C', 'D'],
'C': ['A'], # Cycle: A -> B -> C -> A
'D': []
}
result = has_cycle(graph)
print("Does the graph have a cycle?", result)
Does the graph have a cycle? True
تشخیص مولفههای قویا همبند گراف
الگوریتم DFS به عنوان یکی از الگوریتمهای پیمایش گراف میتواند برای تشخیص مولفههای قویا همبند در گرافهای جهتدار استفاده شود. این کار به ما کمک میکند تا بخشهایی از گراف که هر دو گره به یکدیگر متصل هستند را شناسایی کنیم. این کاربرد در تحلیل ساختار شبکهها و درک بهتر ارتباطات داخلی مفید است.
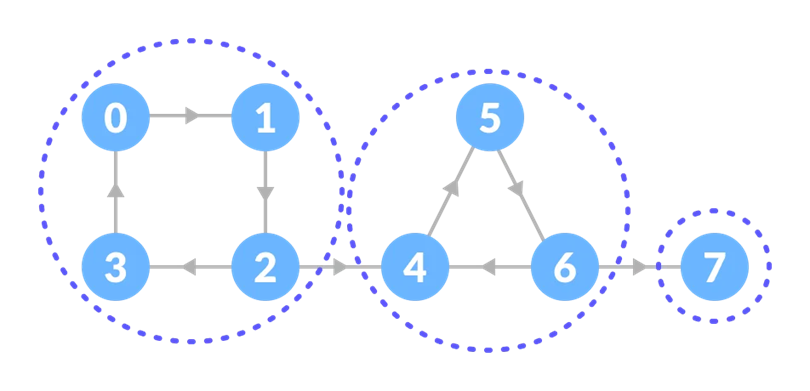

چطور با جستجوی عمق اول مولفههای قویا همبند یک گراف را تشخیص دهیم؟
درواقع الگوریتم DFS در ضمن الگوریتم کساراجو (Kosaraju Algorithm) استفاده میشود. این الگوریتم برای پیدا کردن اجزای قویاً همبند در یک گراف جهتدار استفاده میشود و شامل سه مرحله اصلی است. در مرحله اول، یک پیمایش عمق اول (DFS) بر روی گراف اصلی انجام میشود و گرهها بر اساس زمان پایان بازدیدشان به ترتیب در یک پشته قرار میگیرند. در الگوریتم جستجوی عمق اول، زمان پایان به زمانی اشاره دارد که ما یک گره و تمام همسایههای آن را ملاقات کردهایم. این مفهوم برای مرتبسازی گرهها در گراف استفاده میشود. البته ما دقیقا از زمان استفاده نمیکنیم و ترتیب اتمام کامل پردازش گرهها برایمان مهم است. این ترتیب با استفاده از push کردن گرهها به یک پشته حفظ میگردد.
سپس، جهت یالهای گراف معکوس میشود و در مرحله آخر، یک DFS دیگر بر اساس ترتیب گرههای موجود در پشته روی گراف معکوسشده انجام میشود. در هر بار فراخوانی DFS در این مرحله، یک جز قویا همبند شناسایی و در یک لیست ذخیره میشود. نهایتا، لیستی از تمام اجزای قویا همبند گراف به دست میآید.
پیادهسازی الگوریتم تشخیص مولفههای قویا همبند گراف با جستجوی عمق اول در پایتون
برای پیادهسازی الگوریتم کوساراجو برای یافتن اجزای قویا همبند در یک گراف جهتدار از دو تابع اصلی dfs و reverse_graph استفاده میکنیم. ابتدا در تابع dfs، هر گره را بازدید کرده و به لیست بازدید شدهها اضافه میکنیم. اگر component فراهم شده باشد، گره جاری را به آن اضافه میکنیم. سپس به صورت بازگشتی تمامی همسایههای آن گره را بازدید میکنیم و در نهایت، گره جاری را به پشته اضافه میکنیم.
در مرحله دوم، تابع reverse_graph را تعریف میکنیم که جهت تمامی یالهای گراف ورودی را معکوس میکند. سپس مجموعه بازدید شدهها پاک میشود تا بتوانیم دوباره از آن استفاده کنیم. در مرحله سوم، گرهها را بر اساس ترتیب موجود در پشته (که نشاندهنده ترتیب پایان بازدید در مرحله اول است) بازدید میکنیم. اگر گرهای بازدید نشده باشد، DFS را روی گراف معکوس از آن گره شروع میکنیم و تمامی گرههای مرتبط با آن گره را به لیست component اضافه میکنیم که نشاندهنده یک جزء قویاً همبند است. در نهایت، لیست اجزای قویا همبند برگردانده میشود.
def kosaraju_scc(graph):
def dfs(node, graph, visited, stack=None, component=None):
# Mark the node as visited
visited.append(node)
if component is not None:
# Collect the node if component is provided
component.append(node)
for neighbor in graph[node]:
if neighbor not in visited:
dfs(neighbor, graph, visited, stack, component)
if stack is not None:
# Add the node to the stack after visiting all neighbors
stack.append(node)
def reverse_graph(graph):
reversed_graph = {node: [] for node in graph}
for node in graph:
for neighbor in graph[node]:
reversed_graph[neighbor].append(node)
return reversed_graph
# Step 1: Order nodes by finish time in decreasing order
stack = []
visited = []
for node in graph:
if node not in visited:
dfs(node, graph, visited, stack)
# Step 2: Reverse the graph
reversed_graph = reverse_graph(graph)
# Step 3: Process all nodes in decreasing order of finish time
visited.clear()
sccs = []
while stack:
node = stack.pop()
if node not in visited:
component = []
dfs(node, reversed_graph, visited, component=component)
sccs.append(component)
return sccs
خروجی کد بالا روی گراف زیر را در ادامه میتوانید ببینید:
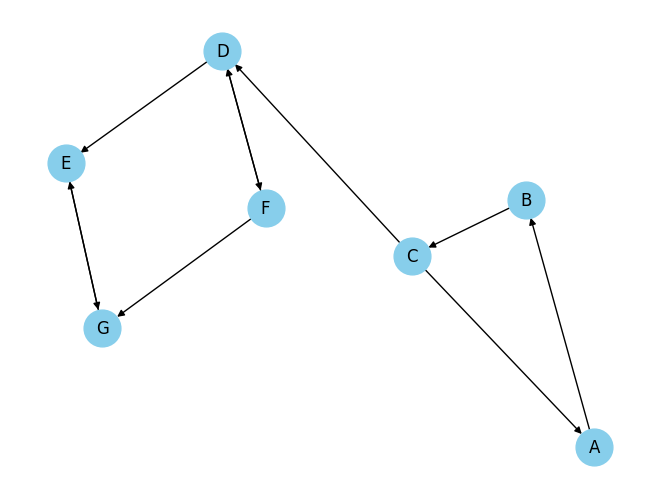

# Define the graph with nodes and directed edges
graph = {
'A': ['B'],
'B': ['C'],
'C': ['A', 'D'],
'D': ['E', 'F'],
'E': ['G'],
'F': ['D', 'G'],
'G': ['E']
}
sccs = kosaraju_scc(graph)
print("Strongly Connected Components:", sccs)
Strongly Connected Components: [[‘A’, ‘C’, ‘B’], [‘D’, ‘F’], [‘E’, ‘G’]]
مرتبسازی توپولوژیکی
یکی از کاربردهای مهم الگوریتم جستجوی عمق اول، مرتبسازی توپولوژیکی (Topological sorting) است. این مرتبسازی برای گرافهای بدون حلقه جهتدار (Directed Acyclic Graph – DAG) استفاده میشود و ترتیب خطی گرهها را به گونهای پیدا میکند که اگر یک گره به گره دیگری اشاره داشته باشد، گره اول قبل از گره دوم قرار گیرد. این الگوریتم در برنامهریزی وظایف، تحلیل پیشنیازها و ساختارهای سلسله مراتبی کاربرد دارد.


چطور با جستجوی عمق اول ترتیب توپولوژیکی یک گراف را پیدا کنیم؟
برای پیدا کردن ترتیب توپولوژیکی یک گراف با استفاده از جستجوی عمق اول، گرهها را بازدید کرده و پس از ملاقات تمامی همسایههای هر گره، آن را به یک پشته اضافه میکنیم. پس از اتمام بازدید از تمامی گرهها، محتوای پشته را که گرهها به ترتیب زمان پایانشان در آن قرار گرفتهاند، معکوس کرده و گرهها را از آن خارج میکنیم. حاصل ترتیب توپولوژیکی گراف را به ما میدهد.
پیادهسازی الگوریتم تشخیص ترتیب توپولوژیکی گراف با جستجوی عمق اول در پایتون
برای پیادهسازی الگوریتم ترتیب توپولوژیکی با استفاده از جستجوی عمق اول (DFS) به عنوان یکی از الگوریتمهای پیمایش گراف از دو تابع اصلی dfs_recursive و topological_sort_dfs استفاده میکنیم. در تابع dfs_recursive، هر گره را بازدید کرده و به لیست بازدید شدهها اضافه میکنیم. سپس به صورت بازگشتی تمامی همسایههای آن گره را بازدید میکنیم. پس از بازدید از تمامی همسایهها، گره جاری را به پشته اضافه میکنیم. در نهایت، با تابع topological_sort_dfs لیستی از گرههای بازدید شده را نگهداری کرده و برای هر گره در گراف، اگر بازدید نشده باشد، تابع dfs_recursive را فراخوانی میکنیم. پس از اتمام بازدید از تمامی گرهها، پشته را معکوس کرده و به عنوان نتیجه برمیگردانیم که نشاندهنده ترتیب توپولوژیکی گراف است:
def dfs_recursive(graph, start, visited=None, stack=None):
# a list to store visited nodes
if visited is None:
visited = []
# mark the node as visited
visited.append(start)
# a stack to keep track of the nodes for topological sorting
if stack is None:
stack = []
# recursively visit all the neighbors of the current node, if the node is unvisited
for neighbor in graph[start]:
if neighbor not in visited:
dfs_recursive(graph, neighbor, visited, stack)
# add the node to the stack after visiting neighbors
stack.append(start)
def topological_sort_dfs(graph):
visited = [] # a list to mark nodes as visited
stack = [] # a stack to store the topological order
# perform DFS algorithm for each node in the graph
for node in graph:
if node not in visited:
dfs_recursive(graph, node, visited, stack)
# return the stack in reverse order for topological sorting
return stack[::-1]
خروجی کد بالا روی گراف زیر را در ادامه میتوانید ببینید:


# Define the graph with nodes
graph = {
'A': ['C', 'D'],
'B': ['D', 'E'],
'C': ['F'],
'D': ['F'],
'E': ['F'],
'F': []
}
topological_order = topological_sort_dfs(graph)
print("Topological Order:", topological_order)
Topological Order: [‘B’, ‘E’, ‘A’, ‘D’, ‘C’, ‘F’]
الگوریتم جستجوی سطح اول
الگوریتم جستجوی سطح اول (Breadth First Search – BFS) به عنوان یکی از الگوریتمهای پیمایش گراف پایهای برای گرافها و درختها است. در این الگوریتم، جستجو از یک نقطه شروع میشود و به صورت سطحی به هر گره همسایه میرود، سپس به سطح بعدی میرود و این فرآیند را تکرار میکند تا تمام گرهها بازدید شوند.
تاریخچه الگوریتم جستجوی سطح اول
الگوریتم جستجوی اول سطح (BFS) در دهه ۱۹۵۰ توسط ادوارد مور و کلود شانون (Claude Shannon) برای مطالعه ماشینهای متناهی (Finite State Machines) و نظریه اطلاعات معرفی شد. در دههٔ ۱۹۷۰، الگوریتم BFS تحت تأثیر پژوهشهای گسترده و بهبودهای مداوم قرار گرفت. یکی از محققین برجسته در این حوزه رابرت تارچن (Robert Tarjan) بود که با بررسی و بهبود الگوریتمهای مرتبط، توانست کاربردهای جدیدی برای BFS ارائه دهد. کارهای تارچن نه تنها بر DFS، بلکه بر BFS نیز تأثیرگذار بود و باعث شد تا این الگوریتم بهعنوان یکی از ابزارهای اصلی در تحلیل و حل مسائل گرافی شناخته شود.
همچنین، BFS در دهههای بعدی به عنوان یکی از اجزای اصلی در بسیاری از سیستمهای اطلاعاتی و شبکههای کامپیوتری توسعه یافت. به ویژه در دهههای اخیر، با پیشرفت فناوری و افزایش نیاز به تحلیل شبکههای پیچیده، BFS بهطور گسترده در زمینههایی همچون هوش مصنوعی، دادهکاوی، و شبکههای اجتماعی به کار گرفته شد.
خروجی الگوریتم جستجوی سطح اول
هنگامی که الگوریتم جستجوی سطح اول یا همان BFS از یک گره شروع به کار میکند و به تمامی گرههای قابل دسترس در گراف میرود، مسیری از گرهها و یالها تشکیل میشود که میتواند به عنوان یک درخت پوشا درنظرگرفته شود. این درخت پوشا شامل تمامی گرههای گراف میشود و حداقل تعداد یالها را دارد بهطوری که تمام گرهها به هم متصل باشند و هیچ حلقهای در گراف ایجاد نشود.
الگوریتم جستجوی سطح اول چطور کار میکند؟
الگوریتم BFS از یک گره شروع میکند که به عنوان گره آغازین انتخاب میشود. این گره میتواند هر گرهای از گراف باشد. در بیشتر پیادهسازیها، این گره به عنوان گره «ریشه» یا گره «مبدا» شناخته میشود. از گره مبدا، به تمامی گرههای همسایه پیش میرویم. این فرایند تا زمانی ادامه پیدا میکند که به یک گره برسیم که هیچ همسایهای نداشته باشد که هنوز بازدید نشده باشد. این به معنای پیشروی به سطح بعدی گراف است. زمانی که به گرهی میرسیم که هیچ همسایهای ندارد که هنوز ملاقات نشده باشد، به گره قبلی بازمیگردیم و دیگر همسایههای آن را بررسی میکنیم. گرههای پیمایش شده را علامتگذاری میکنیم تا از بازدید مجدد آنها جلوگیری شود. این علامتگذاری میتواند با استفاده از یک مجموعه یا لیست (اغلب بهنام visited) انجام شود.


بررسی گامبهگام مراحل اجرای الگوریتم جستجوی سطح اول
حال بیایید کمی عمیقتر روند اجرای الگوریتم BFS را مرور کنیم. برای این منظور فرض کنید یک گراف بهشکل زیر داریم:


گسترش گره
برای اجرای الگوریتم BFS نیاز به یک صف (queue) و یک لیست بهنام visited برای علامتگذاری گرهها بهعنوان ملاقاتشده داریم. در گام نخست یک گره دلخواه را انتخاب کرده (مثلا گره صفر) و آن را در صف قرار میدهیم (queue.enqueue). سپس چون گره دیگری در صف نیست، همین گره را گسترش میدهیم، بهاین معنی که آن را از صف خارج (queue.dequeue) و – درصورتی که تاکنون ملاقات نشده – بهعنوان ملاقات شده علامتگذاری میکنیم.
پردازش گره و تولید همسایههای آن
اکنون میتوانیم گره را پردازش کنیم. عمل پردازش میتواند هرچیزی باشد، مثلا چاپ نام گره یا هر عملیات دیگری که مد نظر ما است. حال باید همسایههایی از گره صفر را که ملاقات نشدهاند، تولید کنیم. دراینجا تولید کردن بهاین معنی است که آنها را در صف قرار دهیم:
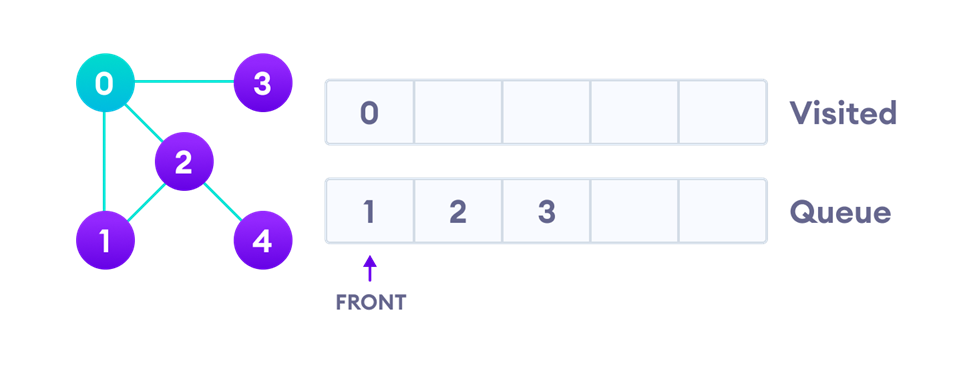

اکنون باید همسایهای از گره صفر که در سر صف (سمت چپ) قرار دارد را گسترش دهیم، یعنی گره یک. همانطور که گفتیم، گسترش یعنی گره را از صف خارج و سپس اگر تابهحال ملاقات نشده، آن را در لیست ملاقاتشدهها قرار دهیم:
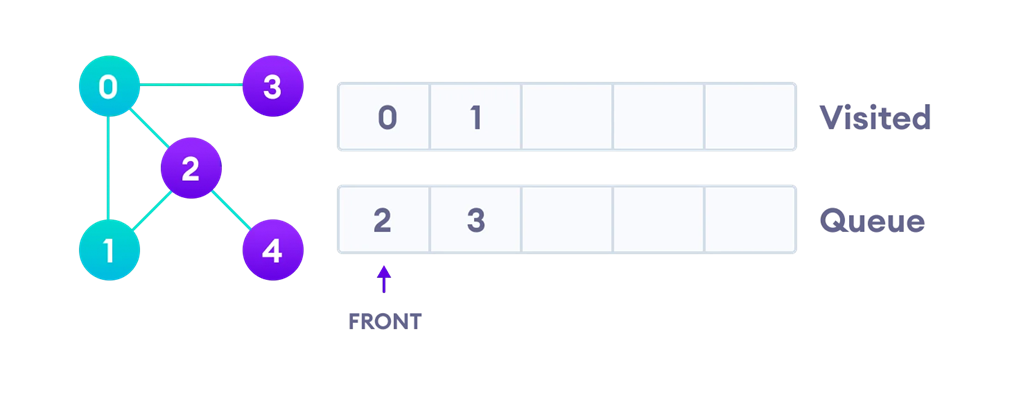

تکرار مراحل بالا برای سایر گرهها
در مرحله بعد باید گره یک را پردازش کرده و همسایههای از آن را که هنوز ملاقات نشدهاند، در انتهای صف قرار دهیم. همسایههای گره یک گرههای صفر و دو هستند که از بین آنها گره صفر ملاقاتشده و گره دو هم قبلا در صف قرار گرفته است، بههمین درشکل بالا دلیل دوباره آن را در انتهای صف قرار نمیدهیم. البته بعدا در پیادهسازی کد این الگوریتم نشان خواهیم داد که درچنین شرایطی واقعا گره دو مجددا وارد صف میشود (چون هنوز ملاقات نشده) اما این موضوع روند اجرای الگوریتم را با مشکل روبهرو نمیکند چون پیش از آنکه دوباره آن را پردازش کنیم، بررسی میکنیم که در لیست ملاقاتشدهها هست یا خیر و اگر قبلا یک بار بهعنوان ملاقاتشده علامتگذاری شده باشد، دوباره پردازش نمیشود.
اکنون سراغ گره شماره دو که سر صف قرار دارد میرویم و آن را گسترش میدهیم. به این ترتیب از صف خارج شده و در لیست ملاقاتشدهها قرار میگیرد. بعد از پردازش، همسایههایی از گره دو را که هنوز ملاقاتنشدهاند (یعنی فقط گره چهار) در انتهای صف قرار میدهیم:
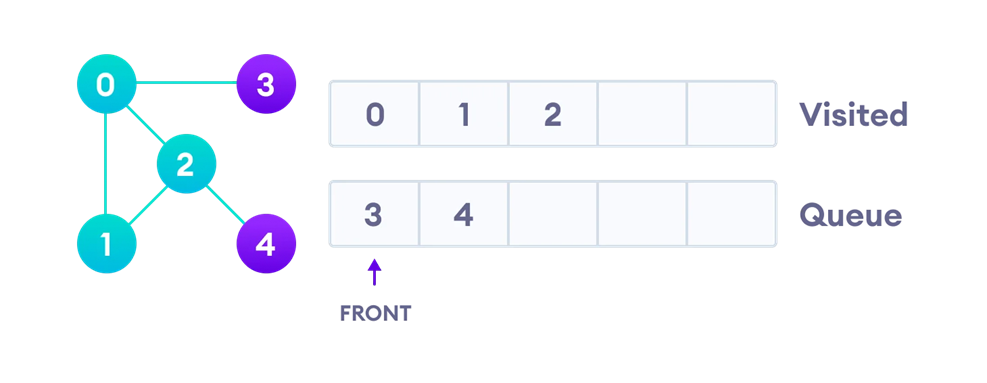

در قسمت بعد گره سه را که در سر صف قرار دارد، گسترش میدهیم. به این ترتیب گره سه در لیست ملاقاتشدهها قرار میگیرد و چون تنها همسایهاش (یعنی گره صفر) قبلا بهعنوان ملاقاتشده علامت خورده، کار دیگری انجام نمیشود:
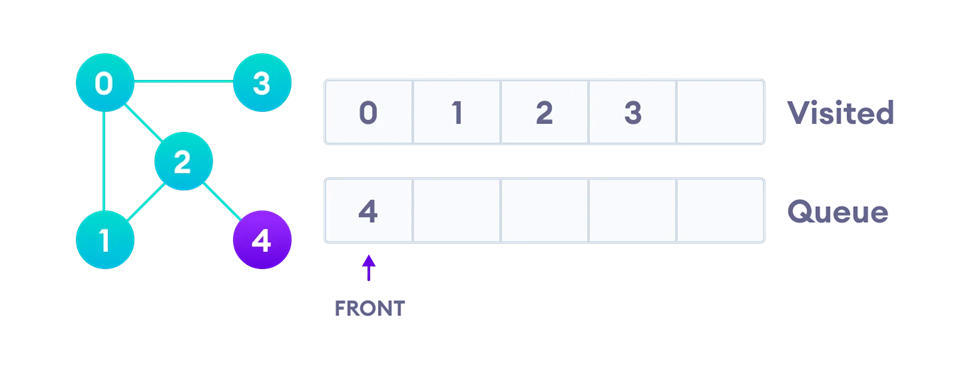

حال تنها گره چهار باقیمانده است. این گره نیز گسترش یافته و از صف خارج میشود. سپس در لیست ملاقاتشدهها قرار میگیرد و چون تنها همسایهاش که گره یک است نیز قبلا ملاقات شده، کار دیگری انجام نمیشود:


با خالی شدن صف، الگوریتم جستجوی سطح اول به پایان میرسد.
پیادهسازی الگوریتم جستجوی سطح اول در پایتون
پیادهسازی الگوریتم BFS میتواند به صورت بازگشتی یا غیربازگشتی انجام شود. در روش بازگشتی، از فراخوانی توابع استفاده میشود، درحالیکه در روش غیربازگشتی، از یک ساختار دادهای صف بهصورت صریح استفاده میشود.
پیادهسازی الگوریتم جستجوی سطح اول به صورت غیربازگشتی
درادامه، الگوریتم جستجوی سطح اول (BFS) را با استفاده از زبان برنامهنویسی پایتون و گرافی که در بالا آن را بهعنوان نمونه بررسی کردیم، پیادهسازی خواهیم کرد. این مثال به شما کمک میکند تا با فرآیند این الگوریتم بهخوبی آشنا شوید و بتوانید آن را در مسائل مختلف بهکار بگیرید.
برای این منظور ابتدا یک تابع بهنام bfs_iterative تعریف میکنیم که گراف مورد نظر و گره شروع (یک گره دلخواه) را بهعنوان ورودی دریافت میکند. در ابتدای این تابع یک لیست بهنام visited تعریف میکنیم که همانطور که توضیح دادیم، نقش ذخیره گرههای بازدیدشده را دارد. با استفاده از کتابخانه collections یک صف فراخوانی کرده و با نام queue در تابع خود تعریف میکنیم که بعد از تولید همسایههای گره جاری، آنها در آن صف قرار دهیم. سپس در یک حلقه while که تا خالیشدن کامل صف برقرار خواهد بود، گره جاری را گسترش میدهیم. یعنی آن را از صف خارج کرده و در صورتی که تاکنون ملاقات نشده، آن را به لیست ملاقاتشدهها اضافه میکنیم. اکنون میتوان گره ملاقاتشده را پردازش کرد. ما در اینجا برای سادگی عمل پردازش را چاپ گره تعریف میکنیم. در پایان نیز همسایههای ملاقاتنشده گره را به صف اضافه میکنیم:
from collections import deque
def bfs_iterative(graph, start):
# a list to store visited nodes
visited = []
# put the initial node in the queue
queue = deque([start])
# repeat until the queue is empty
while queue:
# dequeue the first node from the queue
node = queue.popleft()
# check if the node is not visited
if node not in visited:
# mark the node as visited
visited.append(node)
print(f'Process node: {node}') # or any other process
# enqueue all unvisited neighbors
queue.extend([n for n in graph[node] if n not in visited])
print(f'Queue: {list(queue)}, Visited: {visited}\n')
خروجی کد بالا روی گراف طراحیشده بهصورت زیر است:
# Define the graph with nodes
graph = {
0: [1, 2, 3],
1: [0, 2],
2: [0, 1, 4],
3: [0],
4: [2]
}
bfs_iterative(graph, 0)
Process node: 0
Queue: [1, 2, 3], Visited: [0]
Process node: 1
Queue: [2, 3, 2], Visited: [0, 1]
Process node: 2
Queue: [3, 2, 4], Visited: [0, 1, 2]
Process node: 3
Queue: [2, 4], Visited: [0, 1, 2, 3]
Process node: 4
Queue: [], Visited: [0, 1, 2, 3, 4]
بررسی خروجی الگوریتم جستجوی سطح اول به صورت غیربازگشتی
همانطور که در خروجی این کد میبینید، روندی که در قسمت قبل روی شکل آن را توضیح دادیم در این قسمت نیز اجرا شده است. با هر مرحله از اجرای الگوریتم، گرههای بازدیدشده و صف بهروز میشوند تا همه گرههای گراف بازدید شوند.
نکته قابل توجه ورود دوباره گره دو به صف است، اما چون پیش از پردازش هر گره خارجشده از صف، ابتدا حضورش در لیست ملاقاتشدهها را بررسی میکنیم، با اینکه بعد از پردازش گره سه (خط چهارم خروجی) انتظار داریم مجدداً گره شماره دو پردازش شود، این اتفاق نمیافتد و این گره فقط از صف خارج میشود.
پیادهسازی الگوریتم جستجوی سطح اول به صورت بازگشتی
توضیحات مربوط به اجرای الگوریتم جستجوی سطحی بهصورت بازگشتی نیز تقریبا مشابه حالت غیربازگشتی است. در ادامه، الگوریتم جستجوی سطح اول را به صورت بازگشتی پیادهسازی خواهیم کرد:
def bfs_recursive(graph, queue, visited):
# if the queue is empty, return
if not queue:
return
# dequeue the first node from the queue
node = queue.popleft()
# check if the node is not visited
if node not in visited:
# mark the node as visited
visited.append(node)
print(f'Process node: {node}') # or any other process
# enqueue all unvisited neighbors
for neighbor in graph[node]:
if neighbor not in visited:
queue.append(neighbor)
print(f'Queue: {list(queue)}, Visited: {visited}\n')
# recursively call bfs_recursive with updated queue and visited list
bfs_recursive(graph, queue, visited)
برای مشاهده خروجی کد بالا به صورت زیر عمل میکنیم:
# Define the graph with nodes
graph = {
0: [1, 2, 3],
1: [0, 2],
2: [0, 1, 4],
3: [0],
4: [2]
}
bfs_recursive(graph, deque([0]), [])
Process node: 0
Queue: [1, 2, 3], Visited: [0]
Process node: 1
Queue: [2, 3, 2], Visited: [0, 1]
Process node: 2
Queue: [3, 2, 4], Visited: [0, 1, 2]
Process node: 3
Queue: [2, 4], Visited: [0, 1, 2, 3]
Process node: 4
Queue: [], Visited: [0, 1, 2, 3, 4]
کاربردهای الگوریتم جستجوی سطح اول
الگوریتم جستجوی سطح اول (BFS) یکی از الگوریتمهای پایهای و مهم در نظریه گرافها و علوم کامپیوتر است که کاربردهای فراوانی در مسائل مختلف دارد. در ادامه به بررسی برخی از مهمترین کاربردهای این الگوریتم خواهیم پرداخت:
یافتن مسیر در گراف با استفاده از جستجوی سطح اول
یکی دیگر از کاربردهای الگوریتم BFS، یافتن یک مسیر از یک گره به گره دیگر در یک گراف است. BFS گرهها را به ترتیب سطح بازدید میکند تا به گره هدف برسد. این روش در مسائلی که نیاز به بررسی کوتاهترین مسیر از یک نقطه شروع تا یک نقطه هدف داریم، مفید است.
چطور با جستجوی سطح اول یک مسیر را در یک گراف پیدا کنیم؟
برای یافتن یک مسیر در یک گراف با استفاده از جستجوی سطح اول همان الگوریتم اصلی BFS را اجرا میکنیم. در این حالت، پردازش گره به معنای بررسی هدف بودن آن گره است و شرط توقف الگوریتم، رسیدن به گره هدف یا خالی شدن صف است.
پیادهسازی الگوریتم یافتن مسیر در گراف با جستجوی سطح اول در پایتون
برای پیادهسازی الگوریتم یافتن مسیر در یک گراف با استفاده از جستجوی سطح اول از تابع bfs_search استفاده میکنیم. در این تابع، از یک صف برای نگهداری گرهها استفاده میکنیم. گره شروع را به صف اضافه میکنیم و سپس گرهها را از صف خارج کرده و همسایههای آنها را به صف اضافه میکنیم. اگر در طی این بازدید به گره هدف برسیم، جستجو متوقف میشود و True برگردانده میشود. در غیر این صورت، جستجو ادامه مییابد تا زمانی که صف خالی و False برگردانده میشود:
def bfs_search(graph, start, target):
# a list to store visited nodes
visited = []
# put the initial node in the queue
queue = deque([start])
# repeat until the queue is empty
while queue:
# dequeue the first node from the queue
node = queue.popleft()
# process the node
if node == target:
return True
# check if the node is not visited
if node not in visited:
# mark the node as visited
visited.append(node)
# enqueue all unvisited neighbors
queue.extend([n for n in graph[node] if n not in visited])
return False
خروجی کد بالا روی گراف مورد نظر را به صورت زیر میتوان دید:
# Define the graph with nodes
graph = {
0: [1, 2, 3],
1: [0, 2],
2: [0, 1, 4],
3: [0],
4: [2]
}
# Call the function to search for the target node
result = bfs_search(graph, 0, 4)
print("Found target:", result)
Found target: True
با استفاده از الگوریتمهای یافتن مسیر در هر دو جستجوی سطح اول و عمیق اول، میتوان مسائلی چون پازلهای ماز، مکعب روبیک و ۸ پازل را حل کرد. در واقع در این مسائل از الگوریتمهای جستجوی مسیر برای پیدا کردن توالی حرکتها برای رسیدن به حالت هدف استفاده میشود.
یافتن کوتاهترین مسیر در گرافهای بیوزن
یکی از کاربردهای مهم الگوریتم جستجوی سطح اول به عنوان یکی از الگوریتمهای پیمایش گراف یافتن کوتاهترین مسیر در گرافهای بیوزن است. این الگوریتم تضمین میکند که کوتاهترین مسیر از گره شروع به هر گره دیگری را پیدا کند. این ویژگی در مسائل مختلفی مانند مسیریابی در نقشهها، شبکههای کامپیوتری و بازیهای کامپیوتری مفید است.
چطور با جستجوی سطح اول کوتاهترین مسیر را در یک گراف بیوزن را پیدا کنیم؟
برای پیدا کردن کوتاهترین مسیر در یک گراف بیوزن، از جستجوی سطح اول (BFS) استفاده میکنیم. در واقع با اجرای خود الگوریتم BFS روی گراف بیوزن میتوان کوتاهترین مسیر را پیدا کرد زیرا در این الگوریتم وقتی هر گره را به لیست بازدید شدهها و همسایههای بازدیدنشده آن را به صف اضافه میکنیم، هر گره با کمترین تعداد یالها به گرههای دیگر متصل میشود. به این ترتیب هنگامی که به گره هدف برسیم، کوتاهترین مسیر پیدا شده است.
پیادهسازی الگوریتم یافتن کوتاهترین مسیر گراف بیوزن با جستجوی سطح اول در پایتون
برای پیادهسازی الگوریتم یافتن کوتاهترین مسیر در یک گراف بیوزن با استفاده از جستجوی سطح اول به عنوان یکی از الگوریتمهای پیمایش گراف از تابع اصلی bfs_shortest_path استفاده میکنیم. در این تابع، از یک صف برای نگهداری گرهها و مسیرهای طی شده تا رسیدن به آنها استفاده میکنیم. گره شروع را به همراه مسیر اولیهاش به صف اضافه میکنیم و سپس گرهها را از صف خارج کرده و همسایههای آنها را به صف اضافه میکنیم. اگر در طی این بازدید به گره هدف برسیم، مسیر طی شده را برمیگردانیم. در غیر این صورت، گره فعلی را به لیست بازدید شدهها اضافه میکنیم و همسایههای بازدید نشده را به صف اضافه میکنیم:
def bfs_shortest_path(graph, start, target):
# a list to store visited nodes
visited = []
# put the initial node in the queue and the path taken to reach it
queue = deque([(start, [start])])
while queue:
# dequeue a node and the path taken to reach it
node, path = queue.popleft()
# If the target node is found, return the path
if node == target:
return path
# If the node has not been visited, mark it as visited
if node not in visited:
visited.append(node)
# Enqueue all adjacent nodes that have not been visited
for neighbor in graph[node]:
if neighbor not in visited:
queue.append((neighbor, path + [neighbor]))
return []
خروجی کد بالا روی گراف زیر را در ادامه میتوانید ببینید:
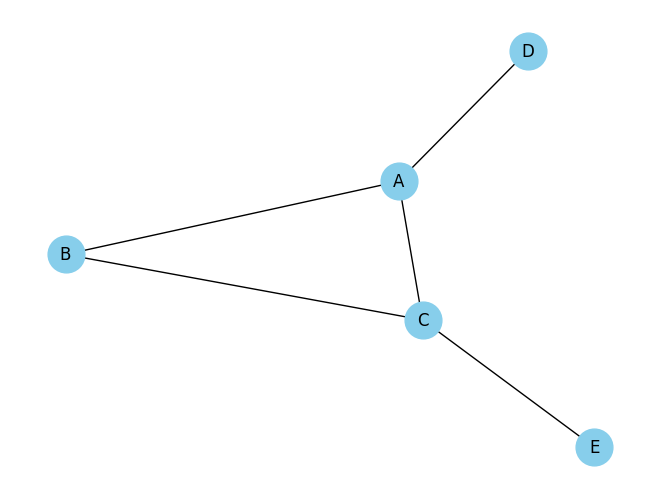

# Define the graph with nodes and edges
graph = {
'A': ['B', 'C', 'D'],
'B': ['A', 'C'],
'C': ['A', 'B', 'E'],
'D': ['A'],
'E': ['C']
}
# Find the shortest path from node 0 to node 4
shortest_path = bfs_shortest_path(graph, 'A', 'E')
print("Shortest path from A to E:", shortest_path)
Shortest path from A to E: [‘A’, ‘C’, ‘E’]
تشخیص دو بخشی بودن گراف
الگوریتم BFS نیز میتواند برای تشخیص دو بخشی بودن گراف استفاده شود. همانطور که گفتیم گراف دو بخشی به گرافی گفته میشود که میتوان گرههای آن را به دو مجموعه مجزا تقسیم کرد به گونهای که هیچ دو گرهای در داخل یک مجموعه به هم متصل نباشند. این کاربرد در مسائل مختلفی مانند تخصیص منابع و شبکههای ارتباطی مفید است.
چطور با جستجوی سطح اول تشخیص دهیم یک گراف دو بخشی است؟
برای تشخیص دو بخشی بودن یک گراف با استفاده از جستجوی سطح اول (BFS)، ابتدا یک صف ایجاد کرده و گره شروع را با یک رنگ مشخص (مثلاً رنگ ۰) به صف اضافه میکنیم. سپس، تا زمانی که صف خالی نشده است، گرههای موجود در صف را یکی یکی برداشته و بررسی میکنیم. هر گره را به لیست بازدید شدهها اضافه کرده و با رنگ مخالف رنگ گره فعلی، همسایههای آن را رنگآمیزی میکنیم. اگر در طی فرآیند رنگآمیزی به گرهای برسیم که رنگ آن با رنگ فعلی مطابقت داشته باشد، گراف دو بخشی نیست. در غیر این صورت، اگر بتوانیم همه گرهها را بدون تناقض رنگآمیزی کنیم، گراف دو بخشی است.
پیادهسازی الگوریتم تشخیص دو بخشی بودن گراف با جستجوی سطح اول در پایتون
برای پیادهسازی الگوریتم تشخیص دو بخشی بودن گراف با استفاده از جستجوی سطح اول (BFS) از دو تابع اصلی bfs_bipartite و is_bipartite استفاده میکنیم. در تابع bfs_bipartite، هر گره را با رنگی (کدشده با ۰ و ۱) مشخص میکنیم و سپس با استفاده از صف (queue) همسایههای آن گره را با رنگ مخالف بازدید میکنیم. اگر در طی این بازدید به گرهای برسیم که قبلاً بازدید شده و رنگ آن با رنگ فعلی مطابقت داشته باشد (یعنی رنگ یک گره با رنگ همسایهاش یکی شود)، گراف دو بخشی نیست و تابعFalse برمیگرداند. در غیر این صورت، پس از بازدید از تمامی همسایهها، تابع True برمیگرداند. تابع is_bipartite مجموعهای از گرههای بازدید شده را نگهداری میکند و برای هر گره در گراف، اگر بازدید نشده باشد، تابع bfs_bipartite را با رنگ ابتدایی ۰ فراخوانی میکند. اگر گراف دو بخشی باشد، True برمیگرداند، در غیر این صورت False برمیگرداند:
def bfs_bipartite(graph, start, colors, visited):
# put the initial node in the queue with color 0
queue = deque([(start, 0)])
while queue:
node, color = queue.popleft()
if node in colors:
# if the node is already colored and the color doesn't match, return False
if colors[node] != color:
return False
else:
# color the node
colors[node] = color
# mark the node as visited
visited.append(node)
# enqueue all unvisited neighbors with the opposite color
for neighbor in graph[node]:
if neighbor not in visited:
queue.append((neighbor, 1 - color))
return True
def is_bipartite(graph):
# dictionary to store the colors of nodes
colors = {}
# list to store visited nodes
visited = []
# iteratively visit all the unvisited nodes of the graph
for node in graph:
if node not in visited:
if not bfs_bipartite(graph, node, colors, visited): # start BFS with color 0
return False
return True
خروجی کد بالا روی گراف زیر را در ادامه میتوانید ببینید:
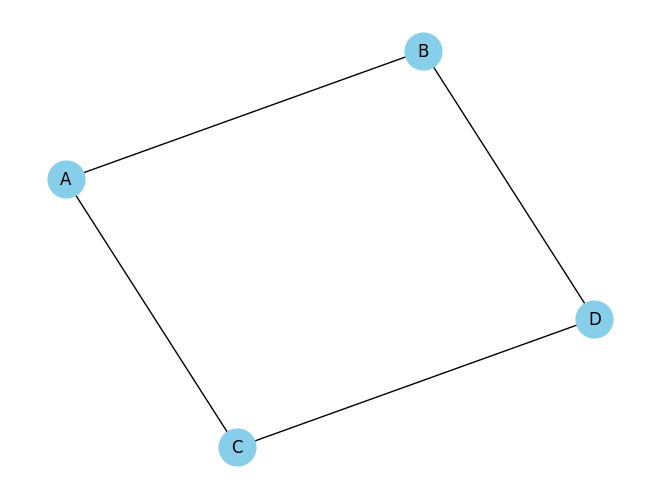

# Define the graph with nodes and edges
graph = {
'A': ['B', 'C'],
'B': ['A', 'D'],
'C': ['A', 'D'],
'D': ['B', 'C']
result = is_bipartite(graph)
print("Is the graph bipartite?", result)
Is the graph bipartite? True
مجموعه کامل کدهای استفاده شده در این مطلب، از گیتهاب ریپوزیتوری Graph Traversal قابل دسترسی است.
جمعبندی الگوریتمهای پیمایش گراف
در جدول زیر میتوانید جمعبندی نکاتی که در بالا برای الگوریتمهای پیمایش گراف مطرح شد را ببینید. البته دقت کنید که هر یک از این دو الگوریتم کاربردهای دیگری نیز دارند اما ما در این بخش مهمترین آنها را بررسی کردیم:
| نوع الگوریتم | ساختار دادهای مورد استفاده | کاربردها | توضیحات الگوریتم |
| جستجوی عمق اول | پشته (Stack) | تشخیص مولفههای قویاً همبند، تشخیص دو بخشی بودن گراف، تشخیص دور در گراف، تشخیص وجود مسیر | از یک گره شروع کرده و به عمق هر شاخه میرود تا زمانی که به یک گره بدون همسایه بازدید نشده برسد، سپس به گرههای قبلی بازمیگردد و مسیرهای دیگر را بررسی میکند. |
| جستجوی سطح اول | صف (Queue) | یافتن کوتاهترین مسیر در گرافهای بیوزن، تشخیص دو بخشی بودن گراف، تشخیص وجود مسیر | از یک گره شروع کرده و ابتدا تمامی گرههای همسایه را بازدید میکند و سپس به سطح بعدی میرود، این فرآیند را تکرار میکند تا تمام گرهها بازدید شوند. |
پیچیدگی زمانی و مکانی الگوریتمها
الگوریتمهای جستجوی عمق اول و جستجوی سطح اول هر دو از نظر زمان و فضا دارای پیچیدگیهای مختلفی هستند که بسته به نوع گراف و شرایط اجرای آنها متفاوت است.
پیچیدگی زمانی
پیچیدگی زمانی الگوریتم جستجوی عمق اول به طور کلی O(V + E) است، که در اینجا V تعداد گرهها (راسها) و E تعداد یالها (لبهها) در گراف است. این پیچیدگی به این دلیل است که هر گره و هر یال دقیقاً یک بار در طول اجرای الگوریتم بازدید میشوند.
پیچیدگی زمانی الگوریتم جستجوی سطح اول نیز O(V + E) است، چرا که مانند DFS هر گره و هر یال دقیقاً یک بار در طول اجرای الگوریتم بازدید میشوند.
پیچیدگی فضایی
پیچیدگی فضایی الگوریتم DFS به دلیل استفاده از پشته (stack) برای نگهداری مسیرهای بازگشتی،O(V) است. در بدترین حالت، عمق پشته برابر با تعداد گرههای گراف میشود.
پیچیدگی فضایی الگوریتم BFS به دلیل استفاده از صف (queue) برای نگهداری گرههای همسایه، O(V) است. در بدترین حالت، تعداد گرههای موجود در صف میتواند برابر با تعداد گرههای یک سطح از گراف باشد.
مقایسه عملکرد الگوریتمها در انواع مختلف گرافها
گرافهای پراکنده
در گرافهای پراکنده (Sparse Graphs) که تعداد یالها حدودا برابر با تعداد گرههاست (E = V) هر دو الگوریتم DFS و BFS عملکرد خوبی دارند و پیچیدگی زمانی هر دو O(V) است. فضای مورد نیاز نیز به تعداد گرهها محدود میشود.
گرافهای متراکم
در گرافهای متراکم (Dense Graphs) که تعداد یالها تقریباً برابر با مجذور تعداد گرههاست (E = V2)، هر دو الگوریتم DFS و BFS پیچیدگی زمانی O(V2) خواهند داشت. دقت کنید که بیشینه تعداد یالها در یک گراف بیجهت V(V-1)/2 و در گرافهای جهتدار V(V-1) است که در هر دو حالت، از مرتبه V2 خواهند بود. در این حالت، فضای مورد نیاز نیز به تعداد گرهها وابسته است، اما تعداد زیاد یالها ممکن است باعث افزایش زمان اجرای الگوریتمها شود.
با در نظر گرفتن این نکات، میتوان نتیجه گرفت که هر دو الگوریتم DFS و BFS در گرافهای پراکنده و متراکم پیچیدگیهای زمانی و فضایی مشابهی دارند. اما انتخاب مناسب بین این دو الگوریتم بستگی به نوع مسئله و نیازمندیهای خاص آن دارد.
در جدول زیر میتوانید جمعبندی نکات گفتهشده در این قسمت را مشاهده نمایید:
| نوع الگوریتم | پیچیدگی زمانی کلی | پیچیدگی زمانی در گرافهای پراکنده | پیچیدگی زمانی در گرافهای متراکم | پیچیدگی فضایی |
| جستجوی عمق اول | O(V + E) | O(V) | O(V2) | O(V) |
| جستجوی سطح اول | O(V + E) | O(V) | O(V2) | O(V) |
مزایا و معایب الگوریتمهای DFS و BFS
در این قسمت مزایا و معایب هر یک از الگوریتمهای پیمایش گراف مطرحشده را بررسی میکنیم:
مزایای الگوریتم DFS
- کارایی حافظه: DFS معمولاً به حافظه کمتری نسبت به BFS نیاز دارد، زیرا فقط نیاز به ذخیره مسیر فعلی دارد و عمق گراف را به صورت پشته مدیریت میکند.
- پیمایش عمیقتر: در مسائل خاصی که نیاز به بررسی عمیقتر گراف دارند، DFS انتخاب مناسبی است.
- ساده برای پیادهسازی: الگوریتم DFS ساده و به راحتی قابل پیادهسازی است.
- کاربردهای گسترده در درختها: DFS در پیمایشهای پیشمرور، پسمرور و میانمرور درختها بهطور گسترده استفاده میشود.
- کاربرد در جستجوی پازلها و بازیها: DFS برای حل مسائل پازلی و بازیهایی که نیاز به بررسی تمامی حالات دارند مناسب است.
معایب الگوریتم DFS
- احتمال رفتن به عمق بینهایت: در گرافهای با حلقههای بینهایت، DFS ممکن است به عمق بینهایت برود و در حلقههای نامحدود گرفتار شود.
- عدم تضمین یافتن کوتاهترین مسیر: DFS تضمینی برای پیدا کردن کوتاهترین مسیر بین دو گره ندارد، زیرا ممکن است به مسیرهای طولانیتری رفته و زودتر به جواب برسد.
- حساسیت به ترتیب گرهها: کارایی DFS به ترتیب بررسی گرهها بستگی دارد و ممکن است در برخی موارد مسیرهای بهینه را نادیده بگیرد.
- پیچیدگی زمانی در بدترین حالت: در گرافهای بزرگ و پیچیده، پیچیدگی زمانی DFS میتواند در بدترین حالت به اندازهٔ کل تعداد گرهها باشد.
مزایای الگوریتم BFS
- جلوگیری از گیر افتادن در حلقههای بینهایت: با استفاده از BFS، احتمال گرفتار شدن در حلقههای بینهایت کمتر است، زیرا گرهها در لحظه بازدید میشوند و از بازدید مجدد آنها جلوگیری میشود.
- پیادهسازی ساده و کارآمد: ساختار ساده الگوریتم BFS و استفاده از صف برای مدیریت گرهها باعث میشود که پیادهسازی آن نسبتاً ساده و سرراست باشد.
- پشتیبانی از پیمایش تمام گرهها: در مواقعی که نیاز به پیمایش و بررسی تمامی گرهها داریم، BFS به دلیل کامل بودن پیمایش سطح به سطح، مناسب است.
معایب الگوریتم BFS
- کارایی کمتر در گرافهای عمیق: در گرافهایی که عمق زیادی دارند و عرض کمتری دارند، BFS ممکن است کارایی کمتری نسبت به DFS داشته باشد. زیرا این الگوریتم تمام گرههای یک سطح را پیش از رفتن به عمق بررسی میکند که میتواند کارایی را کاهش دهد.
- عدم توانایی در یافتن مسیرهای پیچیده: BFS بهطور طبیعی برای یافتن کوتاهترین مسیر در گرافهای بدون وزن طراحی شده است، اما ممکن است در یافتن مسیرهای پیچیده و طولانیتر کارایی کمتری داشته باشد.
- حساسیت به ترتیب گرهها: کارایی BFS به ترتیب بررسی گرهها بستگی دارد و ممکن است در برخی موارد مسیرهای بهینه را نادیده بگیرد. ترتیب گرهها در صف میتواند بر عملکرد الگوریتم تأثیر بگذارد.
کلام آخر درباره الگوریتمهای پیمایش گراف
گرافها به عنوان ساختارهای دادهای اساسی، نقش مهمی در مدلسازی و تحلیل ارتباطات پیچیده ایفا میکنند. الگوریتمهای پیمایش گراف مانند جستجوی عمق اول (DFS) و جستجوی سطح اول (BFS) ابزارهای کلیدی برای بازدید و استخراج اطلاعات از این ساختارها هستند. الگوریتم DFS با پیشروی عمقی و الگوریتم BFS با پیشروی سطحی، هر یک به روشی خاص به تحلیل و حل مسائل مختلف در گرافها میپردازند. کاربردهای این الگوریتمهای پیمایش گراف از یافتن کوتاهترین مسیرها در شبکهها تا تشخیص مولفههای قویاً همبند و دو بخشی بودن گرافها، نشاندهنده اهمیت و گستردگی استفاده از آنها در زمینههای مختلف علمی و عملی است. با درک و تسلط بر این الگوریتمها، میتوان به بهبود عملکرد و حل بهینه مسائل پیچیده در دنیای واقعی دست یافت. امید است که این مقاله توانسته باشد شما را با اصول و کاربردهای الگوریتمهای پیمایش گراف آشنا کرده و زمینهای برای پژوهشهای بیشتر در این حوزه فراهم کند.


پرسشهای متداول
الگوریتم جستجوی عمق اول چگونه در یافتن درخت پوشا در گرافها به کار میرود؟
الگوریتم جستجوی عمق اول (DFS) با شروع از یک گره مشخص، به صورت عمقی در گراف پیشروی میکند و تا حد امکان به شاخههای عمیقتر میرود. زمانی که به گرهای برسد که دیگر امکان پیشروی نداشته باشد، به گره قبلی بازمیگردد و مسیرهای دیگر را بررسی میکند. این فرایند تا بازدید از تمامی گرهها ادامه مییابد. خروجی DFS میتواند به عنوان یک درخت پوشا در نظر گرفته شود که شامل تمامی گرههای گراف است و حداقل تعداد یالها را دارد.
چه تفاوتهایی بین الگوریتمهای پیمایش گراف جستجوی عمق اول و جستجوی سطح اول وجود دارد؟
الگوریتم جستجوی عمق اول به صورت عمقی به هر شاخه از گراف پیشروی میکند تا زمانی که به یک گره بدون همسایه بازدید نشده برسد، سپس به گرههای قبلی بازمیگردد. در مقابل، الگوریتم جستجوی سطح اول به صورت سطحی عمل میکند و ابتدا تمامی گرههای همسایه یک گره را بازدید میکند و سپس به سطح بعدی میرود. DFS برای یافتن درخت پوشا و مولفههای قویاً همبند مناسب است، در حالی که BFS برای یافتن کوتاهترین مسیر در گرافهای بیوزن کاربرد دارد.
چگونه میتوان از الگوریتم جستجوی عمق اول برای تشخیص مولفههای قویاً همبند استفاده کرد؟
برای تشخیص مولفههای قویاً همبند (Strongly Connected Components) در گرافهای جهتدار، ابتدا از یک گره دلخواه DFS اجرا میشود و گرهها بر اساس زمان پایان بازدیدشان به ترتیب در یک پشته قرار میگیرند. سپس جهت یالهای گراف معکوس میشود و DFS دیگری بر اساس ترتیب گرههای موجود در پشته روی گراف معکوسشده انجام میشود. هر بار که DFS در این مرحله فراخوانی میشود، یک مولفه قویاً همبند شناسایی میشود.
الگوریتم جستجوی سطح اول چگونه میتواند در یافتن کوتاهترین مسیر در گرافهای بیوزن کمک کند؟
الگوریتم جستجوی سطح اول به عنوان یکی از الگوریتمهای پیمایش گراف به دلیل پیشروی سطحی خود، تضمین میکند که کوتاهترین مسیر از گره شروع به هر گره دیگری را پیدا کند. در این الگوریتم، هر گره به محض بازدید به لیست ملاقاتشدهها اضافه میشود و همسایههای آن در صف قرار میگیرند. این فرایند تا زمانی ادامه مییابد که به گره هدف برسیم، که در این حالت کوتاهترین مسیر به دست میآید.
چه کاربردهایی برای الگوریتم جستجوی عمق اول و جستجوی سطح اول در زمینههای عملی مختلف وجود دارد؟
الگوریتم جستجوی عمق اول (DFS) به عنوان یکی از الگوریتمهای پیمایش گراف در مسائلی مانند تشخیص مولفههای قویاً همبند، یافتن درخت پوشا و تشخیص دو بخشی بودن گراف کاربرد دارد. الگوریتم جستجوی سطح اول (BFS) نیز در مسائلی مانند یافتن کوتاهترین مسیر در گرافهای بیوزن، تشخیص دو بخشی بودن گراف و یافتن مسیرهای ارتباطی در شبکهها به کار میرود. این الگوریتمها به دلیل تواناییشان در تحلیل و پردازش ساختارهای پیچیده گرافی، در بسیاری از زمینههای علمی و عملی مورد استفاده قرار میگیرند.
یادگیری تحلیل داده را از امروز شروع کنید!
دنیای دادهها جذاب است و دانستن علم داده، توانایی تحلیل داده، یا بازاریابی مبتنی بر داده، شما را برای فرصتهای شغلی بسیاری مناسب میکند. فارغ از رشته و پیشزمینه، میتوانید حالا شروع کنید و از سطح مقدماتی تا پیشرفته بیاموزید. اگر دوست دارید به این حوزه وارد شوید، پیشنهاد میکنیم با کلیک روی این لینک قدم اول را همین حالا بردارید.
مشاوران کافهتدریس به شما کمک میکنند مسیر یادگیری برای ورود به این حوزه را شروع کنید:

