توزیع داده و انواع آن در یادگیری ماشین: چرا شناخت آن برای هر داده‌کاوی حیاتی است؟

در دنیای امروز، یادگیری ماشین به یکی از موضوعات بسیار مهم و پرکاربرد تبدیل شده است. اما برای اینکه مدل‌های یادگیری ماشین بتوانند به درستی کار کنند، نیاز به داده‌های مناسب و با کیفیت دارند. یکی از جنبه‌های بسیار مهم داده‌ها، توزیع آن‌ها است. توزیع داده‌ (Data Distribution) می‌تواند به طور مستقیم بر عملکرد و دقت مدل‌ها تاثیر بگذارد. در این مقاله به بررسی توزیع داده و انواع آن در یادگیری ماشین می‌پردازیم و نقش حیاتی آن‌ها را در بهبود عملکرد مدل‌ها مورد بحث قرار می‌دهیم.

 توزیع داده چیست؟

توزیع داده به نحوه پخش و توزیع مقادیر در یک مجموعه داده اشاره دارد. به عبارت دیگر، توزیع داده نشان‌دهنده الگوی مقادیر در داده‌ها است. این الگو می‌تواند به صورت گرافیکی نمایش داده شود و اطلاعات زیادی درباره خصوصیات داده‌ها فراهم کند. برای مثال، می‌تواند نشان دهد که مقادیر داده‌ها بیشتر در چه بازه‌هایی متمرکز هستند یا اینکه داده‌ها تا چه اندازه پراکنده‌اند.

 اهمیت توزیع داده در یادگیری ماشین

توزیع داده تاثیر زیادی بر عملکرد مدل‌های یادگیری ماشین دارد. مدل‌های یادگیری ماشین برای یادگیری الگوها و روابط موجود در داده‌ها به توزیع صحیح و مناسبی از داده‌ها نیاز دارند. اگر توزیع داده‌ها به درستی درک نشود، مدل‌های یادگیری ماشین ممکن است نتایج نادرستی ارائه دهند و در کاربردهای عملی ناکارآمد باشند. به همین دلیل، تحلیل و درک توزیع داده‌ها یکی از گام‌های مهم در فرآیند یادگیری ماشین است.

انواع توزیع داده

توزیع داده‌ها به دو دسته کلی تقسیم می‌شوند: توزیع‌های پیوسته و توزیع‌های گسسته.

 توزیع‌های پیوسته

توزیع‌های پیوسته نقش مهمی در آمار و یادگیری ماشین ایفا می‌کنند. این توزیع‌ها به ما کمک می‌کنند تا داده‌های واقعی را مدل‌سازی کرده و الگوهای موجود در آن‌ها را شناسایی کنیم. پیش از بررسی انواع توزیع‌های پیوسته، لازم است با مفهومی به‌نام تابع چگالی احتمال آشنا شویم زیرا درادامه به‌آن نیاز خواهیم داشت.

تابع چگالی احتمال

تابع چگالی احتمال (PDF – Probability Density Function) یک مفهوم اساسی در نظریه احتمال و آمار است که برای توصیف توزیع احتمال یک متغیر تصادفی پیوسته به کار می‌رود. به بیان ساده، PDF تابعی است که احتمال مشاهده یک مقدار خاص یا یک بازه خاص از یک متغیر تصادفی پیوسته را بیان می‌کند.

حال به‌بررسی انواع توزیع داده پیوسته می‌پردازیم:

توزیع نرمال

توزیع نرمال (Normal Distribution) یا گاوسی یکی از رایج‌ترین توزیع‌های آماری است که بسیاری از پدیده‌های طبیعی از آن پیروی می‌کنند. این توزیع به صورت یک منحنی زنگوله‌ای شکل نمایش داده می‌شود که بیشترین تعداد داده‌ها در مرکز قرار دارند و با فاصله گرفتن از مرکز، تعداد داده‌ها کاهش می‌یابد. درشکل زیر یک نمونه از رسم تابع چگالی احتمال این توزیع آماری را می‌بینید:

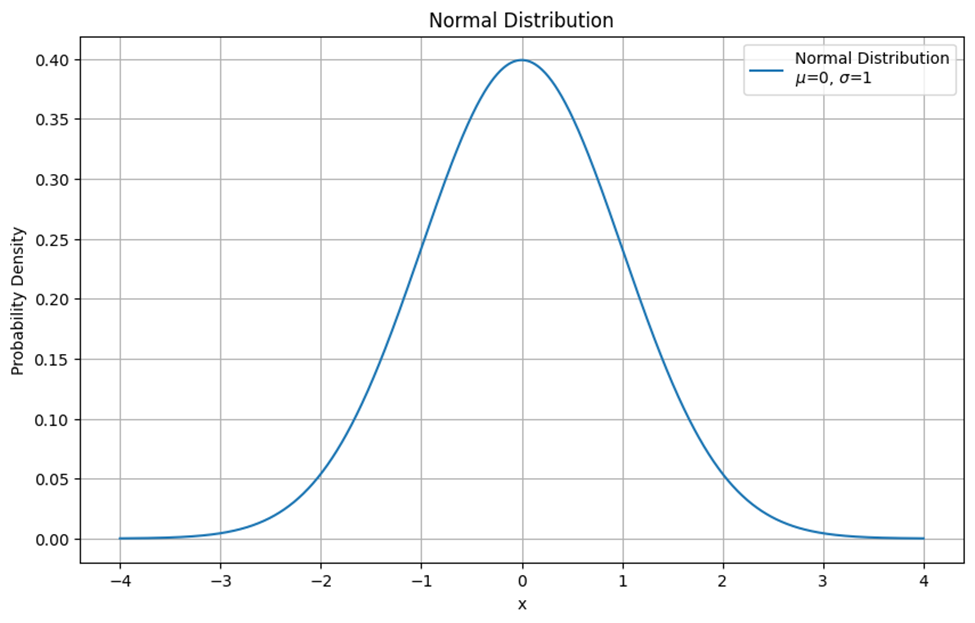
ویژگی‌های توزیع نرمال

توزیع نرمال دارای ویژگی‌هایی از قبیل تقارن حول میانگین، بیشترین تمرکز داده‌ها در نزدیکی میانگین و کاهش تعداد داده‌ها با فاصله گرفتن از میانگین است. این توزیع به طور گسترده در آمار و یادگیری ماشین به کار می‌رود زیرا بسیاری از پدیده‌های طبیعی و داده‌های واقعی از آن پیروی می‌کنند.

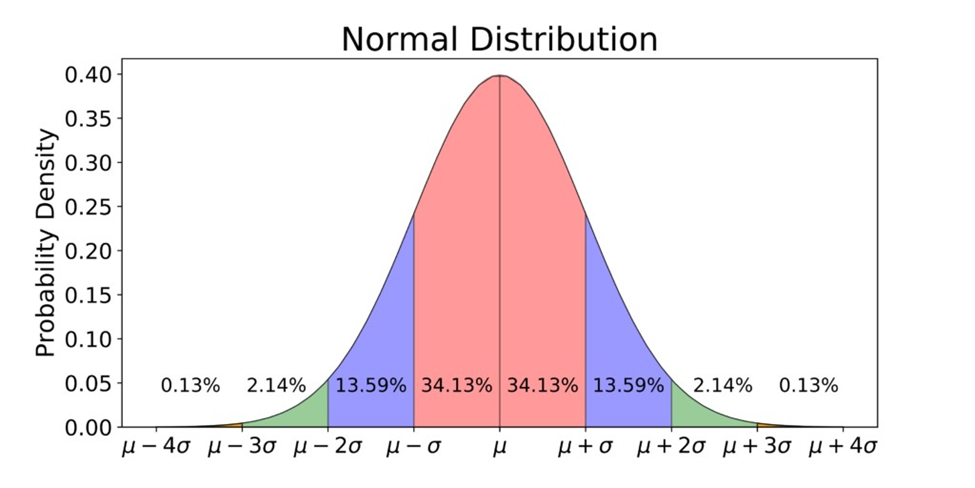
یکی دیگر از ویژگی‌های کلیدی توزیع داده نرمال این است که توزیع به صورت تقارنی حول میانگین قرار دارد و تقریباً ۶۸٪ داده‌ها در فاصله یک انحراف معیار از چپ و راست میانگین (مجموعا دو انحراف معیار)، ۹۵٪ داده‌ها در فاصله دو انحراف معیار از چپ و راست میانگین (مجموعا ۴ انحراف معیار) و ۹۹.۷٪ داده‌ها در فاصله سه انحراف معیار از چپ و راست میانگین (مجموعا ۶ انحراف معیار) قرار دارند.

درستی توضیحات مطرح‌شده در بالا را می‌توانید در شکل زیر بررسی کنید:

فرمول ریاضی

تابع چگالی احتمال توزیع نرمال به صورت زیر تعریف می‌شود:

\large f(x|\mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}

در این فرمول، هر یک از اجزا نقش خاصی در تعیین شکل و ویژگی‌های توزیع نرمال دارد. برای درک بهتر این فرمول، به توضیحات زیر توجه کنید:

میانگین

میانگین یا μ، مرکزی‌ترین نقطه توزیع نرمال است. این مقدار نشان‌دهنده مرکز تقارن توزیع است و تمامی داده‌ها حول این نقطه توزیع می‌شوند. در نمودار توزیع نرمال، μ همان نقطه اوج (Peak) منحنی زنگوله‌ای شکل است.

انحراف معیار

انحراف معیار یا σ، میزان پراکندگی داده‌ها را نسبت به میانگین نشان می‌دهد. هرچه σ بیشتر باشد، داده‌ها پراکندگی بیشتری دارند و منحنی توزیع پهن‌تر خواهد بود. برعکس، اگر σ کوچک‌تر باشد، داده‌ها به میانگین نزدیک‌تر هستند و منحنی توزیع باریک‌تر خواهد بود.

ضریب نرمال‌سازی

این ضریب برای اطمینان از این که مساحت زیر منحنی توزیع نرمال برابر با ۱ باشد، استفاده می‌شود. این اطمینان از این حاصل می‌شود که توزیع نرمال یک توزیع احتمالی معتبر است.

قسمت نمایی

قسمت نمایی فرمول بالا نشان‌دهنده نحوه کاهش مقدار چگالی احتمال با فاصله گرفتن از میانگین است. این قسمت نمایی (exp) به صورت نمایی منفی است و باعث می‌شود که چگالی احتمال به سرعت با فاصله گرفتن از μ کاهش یابد. عبارت  نشان‌دهنده فاصله مقدار x از میانگین به توان دو است که برحسب انحراف معیار نرمال شده است.

کاربردهای توزیع نرمال در یادگیری ماشین

توزیع داده نرمال در بسیاری از الگوریتم‌های یادگیری ماشین به طور گسترده استفاده می‌شود. این توزیع به دلیل ویژگی‌های منحصر به فرد خود، به مدل‌ها کمک می‌کند تا بتوانند الگوهای پیچیده‌تری را از داده‌ها استخراج کرده و پیش‌بینی‌های دقیقی انجام دهند. در ادامه، به توضیح نقش توزیع نرمال در سه الگوریتم مهم یادگیری ماشین می‌پردازیم: رگرسیون خطی (Linear Regression)، تحلیل مولفه‌های اصلی (Principle Component Analysis – PCA) و شبکه‌های عصبی (Neural Networks).

رگرسیون خطی

رگرسیون خطی یکی از ساده‌ترین و پرکاربردترین الگوریتم‌های یادگیری ماشین است که برای مدل‌سازی رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل استفاده می‌شود. در این الگوریتم، فرض می‌شود که خطاها (یا باقی‌مانده‌ها) دارای توزیع نرمال با میانگین صفر و واریانس ثابت هستند. این فرض به مدل کمک می‌کند تا بتواند پیش‌بینی‌های دقیقی انجام دهد و روابط خطی میان متغیرها را به درستی شناسایی کند.

به عنوان مثال، اگر بخواهیم رابطه بین سن و قد افراد را مدل‌سازی کنیم، فرض می‌شود که تفاوت بین قد پیش‌بینی‌شده و قد واقعی (خطاها) دارای توزیع نرمال است. این فرض به ما اطمینان می‌دهد که مدل می‌تواند با دقت بالاتری پارامترهای خط را تخمین بزند.

تحلیل مولفه‌های اصلی

تحلیل مولفه‌های اصلی یا PCA یک تکنیک کاهش بعد است که برای کاهش تعداد متغیرهای ورودی به یک مدل استفاده می‌شود. هدف PCA شناسایی مولفه‌های اصلی (متغیرهای جدید) است که بیشترین واریانس داده‌ها را توضیح می‌دهند. درPCA ، فرض می‌شود که داده‌ها دارای توزیع نرمال هستند.

این فرض به PCA کمک می‌کند تا بتواند مولفه‌های اصلی را به‌درستی شناسایی کند و واریانس داده‌ها را به‌بهترین شکل ممکن توضیح دهد. برای مثال، در یک مجموعه داده با صدها ویژگی، PCA می‌تواند چندین مولفه اصلی را شناسایی کند که به‌طور موثری تمام واریانس داده‌ها را نمایندگی می‌کنند.

شبکه‌های عصبی

شبکه‌های عصبی مدل‌هایی هستند که از ساختارهای الهام‌گرفته از مغز انسان برای یادگیری الگوها و روابط پیچیده در داده‌ها استفاده می‌کنند. در فرآیند آموزش شبکه‌های عصبی، وزن‌های اولیه شبکه معمولاً به صورت تصادفی از یک توزیع نرمال انتخاب می‌شوند. این انتخاب تصادفی به شبکه کمک می‌کند تا فرآیند یادگیری را به درستی آغاز کند و به سمت بهینه‌سازی پارامترها حرکت کند.

توزیع یکنواخت

در حوزه احتمال و آمار، توزیع یکنواخت یک مفهوم اساسی است که اغلب به عنوان یک پل به سمت توزیع‌های پیچیده‌تر عمل می‌کند. این توزیع زمانی استفاده می‌شود که داده‌ها به طور مساوی در بازه‌ای مشخص پخش شده باشند و هیچ مقدار خاصی برتری نداشته باشد. توزیع یکنواخت پیوسته وضعیتی را توصیف می‌کند که در آن هر مقداری در یک بازه مشخص به طور مساوی محتمل است. این توزیع بر یک محدوده پیوسته از مقادیر تعریف می‌شود و آن را به یک نوع توزیع احتمالی پیوسته تبدیل می‌کند.

ویژگی‌های توزیع یکنواخت

در این توزیع، هرمقدار دربازه مشخصی به‌صورت مساوی احتمال وقوع دارد، بنابراین نمودار این توزیع به‌صورت یک مستطیل است که ارتفاع آن نمایانگر احتمال وقوع هر مقدار است. در شکل زیر یک نمونه از ترسیم این تابع چگالی احتمال این توزیع را می‌بینید:

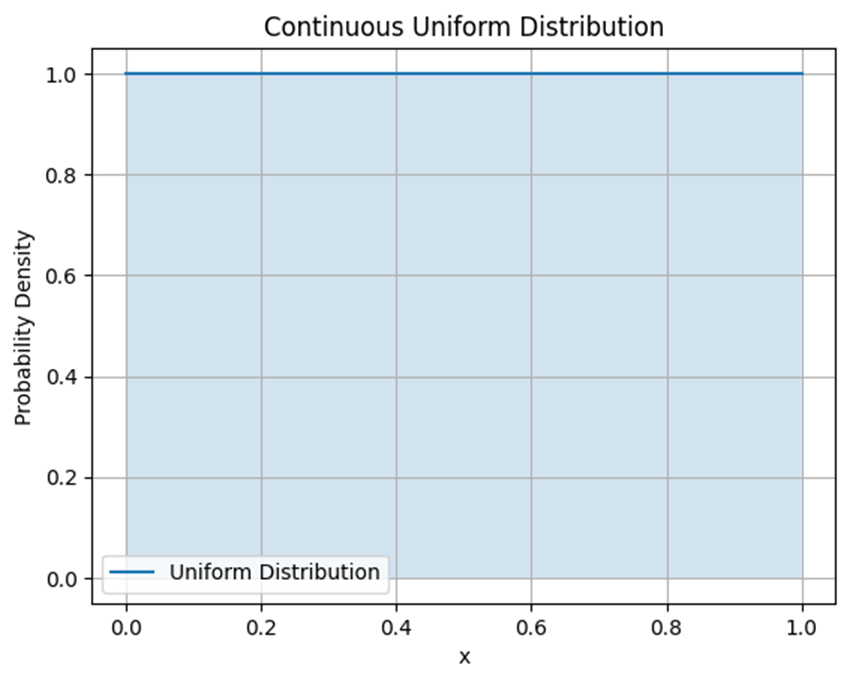
فرمول ریاضی

تابع چگالی احتمال توزیع یکنواخت به صورت زیر تعریف می‌شود:

\large f(x) = \begin{cases} \frac{1}{b-a} & \text{for } a \leq x \leq b \\ 0 & \text{otherwise} \end{cases}

این تابع نشان می‌دهد که احتمال وقوع هر مقدار در بازه [a,b] برابر است با 1/b-a.

کاربردهای توزیع یکنواخت در یادگیری ماشین

توزیع داده یکنواخت در بسیاری از مسائل مربوط به نمونه‌گیری تصادفی، شبیه‌سازی و ایجاد داده‌های مصنوعی مورد استفاده قرار می‌گیرد. این توزیع به ویژه در مسائلی که نیاز به توزیع مساوی داده‌ها در یک بازه مشخص دارند، مفید است. در ادامه به برخی از کاربردهای مهم توزیع یکنواخت در یادگیری ماشین می‌پردازیم:

تولید داده‌های مصنوعی

یکی از کاربردهای اصلی توزیع یکنواخت در یادگیری ماشین، تولید داده‌های مصنوعی است. در بسیاری از موارد، برای آزمایش الگوریتم‌ها و مدل‌های یادگیری ماشین نیاز به داده‌های مصنوعی داریم. توزیع داده یکنواخت به عنوان یک ابزار ساده و قدرتمند برای تولید داده‌های مصنوعی با پراکندگی یکنواخت در یک بازه معین مورد استفاده قرار می‌گیرد. این داده‌ها می‌توانند برای تست عملکرد الگوریتم‌ها در شرایط مختلف استفاده شوند.

نمونه‌گیری تصادفی

در بسیاری از الگوریتم‌های یادگیری ماشین، نمونه‌گیری تصادفی از داده‌ها بخش مهمی از فرآیند یادگیری است. توزیع یکنواخت به دلیل ویژگی‌های خاص خود، برای نمونه‌گیری تصادفی از داده‌ها بسیار مناسب است. این نمونه‌گیری‌ها می‌توانند در انتخاب تصادفی زیرمجموعه‌های داده‌ها برای آموزش مدل‌ها، تقسیم داده‌ها به مجموعه‌های آموزشی و آزمایشی و یا انجام کراس‌ولیدیشن استفاده شوند.

الگوریتم‌های بهینه‌سازی

در الگوریتم‌های بهینه‌سازی تصادفی مانند الگوریتم‌های ژنتیک، الگوریتم‌های تجمعی و الگوریتم‌های جستجوی تصادفی، توزیع یکنواخت برای ایجاد تغییرات تصادفی در پارامترها یا تولید جمعیت اولیه به کار می‌رود. این توزیع به دلیل توانایی ایجاد تغییرات یکنواخت و متوازن در فضای جستجو، به الگوریتم‌ها کمک می‌کند تا به طور مؤثر در فضای پارامترها جستجو کنند و بهینه‌سازی بهتری انجام دهند.

تنظیم پارامترها و جستجوی هایپراپارامترها

توزیع یکنواخت در جستجوی هایپراپارامترها برای تنظیم مدل‌های یادگیری ماشین استفاده می‌شود. به عنوان مثال، در جستجوی شبکه‌ای (Grid Search) و جستجوی تصادفی (Random Search)، توزیع یکنواخت برای انتخاب تصادفی هایپراپارامترها از یک بازه مشخص به کار می‌رود. این روش‌ها به مدل‌ها کمک می‌کنند تا بهترین تنظیمات را برای دستیابی به عملکرد بهینه پیدا کنند.

الگوریتم‌های مونت کارلو

الگوریتم‌های مونت کارلو (Monte Carlo) که برای شبیه‌سازی و تخمین مقادیر پیچیده به کار می‌روند، از توزیع یکنواخت برای تولید نمونه‌های تصادفی استفاده می‌کنند. این الگوریتم‌ها در یادگیری ماشین برای برآورد پارامترها، محاسبه انتگرال‌های چندگانه و حل مسائل بهینه‌سازی پیچیده مورد استفاده قرار می‌گیرند.

توزیع نمایی

توزیع نمایی یکی از توزیع‌های احتمال پیوسته است که به‌طور گسترده در مدل‌سازی زمآن‌های بین وقوع رویدادها در یک فرآیند پوآسون استفاده می‌شود. این توزیع به‌خصوص برای مدل‌سازی زمآن‌های انتظار تا وقوع یک رویداد، مانند زمان بین دو خرابی در سیستم‌های مکانیکی یا الکترونیکی، بسیار مفید است.

ویژگی‌های توزیع نمایی

توزیع نمایی به دلیل کاهش نمایی احتمال وقوع با افزایش فاصله زمانی، به صورت یک نمودار با شیب نزولی نمایش داده می‌شود. درشکل زیر یک نمونه از ترسیم این توزیع را می‌بینید:

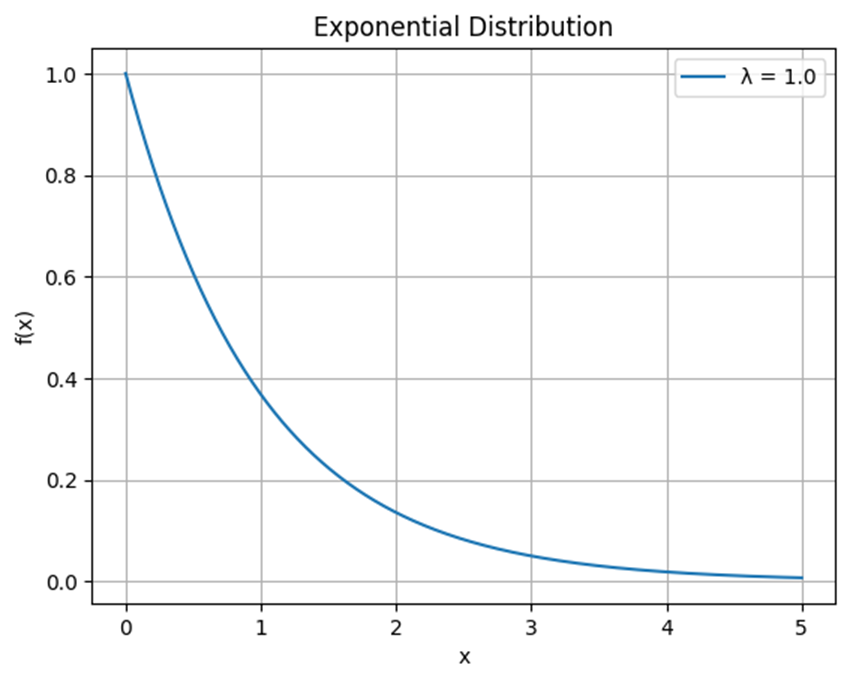
این نمودار از نقطه‌ی (0,λ) شروع می‌شود و با افزایش مقدار x، تابع چگالی احتمال به صورت نمایی کاهش می‌یابد. این بدان معناست که احتمال وقوع رویدادها با گذشت زمان، کاهش می‌یابد.

فرمول ریاضی

تابع چگالی احتمال توزیع نمایی به صورت زیر است:

\large f(x; \lambda) = \begin{cases} \lambda e^{-\lambda x} & \text{for } x \geq 0 \\ 0 & \text{otherwise} \end{cases}

در این فرمول، λ (لامبدا) پارامتر نرخ یا شدت وقوع رویدادها است که باید بزرگتر از صفر باشد. این تابع نشان می‌دهد که احتمال وقوع یک رویداد در فاصله زمانی x پس از رویداد قبلی چقدر است. به عبارت دیگر، اگر x زمان بین دو رویداد متوالی باشد، تابع چگالی احتمال، میزان احتمال وقوع در این زمان را توصیف می‌کند.

به عنوان مثال، اگر در یک سیستم نرخ وقوع خرابی‌ها λ باشد، تابع چگالی احتمال نشان می‌دهد که احتمال خرابی در فاصله زمانی x از خرابی قبلی چقدر است. با افزایش λ، فاصله زمانی بین رویدادها کمتر خواهد بود و رویدادها با سرعت بیشتری رخ خواهند داد.

تحلیل نمودار توزیع نمایی برای نرخ‌های وقوع رویداد مختلف

برای مشاهده تاثیر نرخ وقوع (لامبدا) به نمودار زیر نگاه کنید:

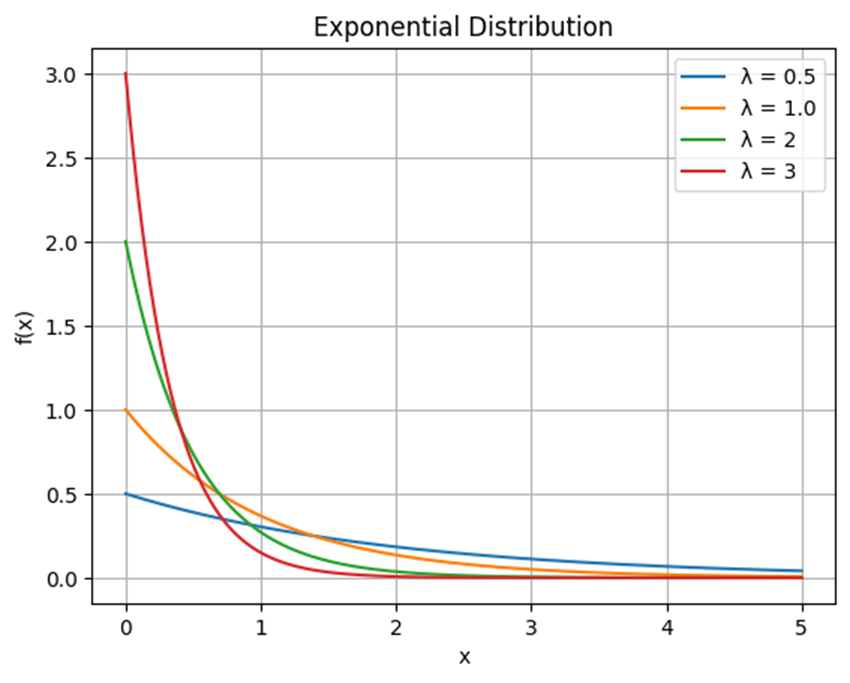
این نمودار به وضوح نشان می‌دهد که با افزایش پارامتر λ، توزیع نمایی سریع‌تر کاهش می‌یابد. برای مثال نمودار با λ=0.5 (خط آبی) کمترین نرخ کاهش را دارد و کندتر از بقیه نمودارها به صفر میل می‌کند. اما نمودار با λ=3 (خط قرمز) سریع‌ترین نرخ کاهش را دارد و نشان می‌دهد که احتمال وقوع رویدادها بسیار سریع کاهش می‌یابد.

کاربردهای توزیع نمایی در یادگیری ماشین

توزیع داده نمایی با ویژگی‌های خاص خود، از جمله حافظه نداشتن و سادگی، ابزاری قدرتمند برای مدل‌سازی و تحلیل در یادگیری ماشین و علوم داده است. این توزیع می‌تواند به بهبود مدل‌ها و الگوریتم‌های یادگیری کمک کند و در نتیجه، نتایج دقیق‌تر و بهینه‌تری ارائه دهد.

یادگیری تقویتی

در حوزه یادگیری تقویتی، توزیع نمایی برای مدل‌سازی زمان بین اقدامات یک عامل (agent) و دریافت پاداش (reward) استفاده می‌شود. این مدل‌ها به بهبود سیاست‌های تصمیم‌گیری و افزایش کارایی یادگیری کمک می‌کنند.

مدل‌های مولد و فرآیندهای تصادفی

در مدل‌های مولد (Generative Models) و به‌ویژه در فرآیندهای تصادفی مانند زنجیره‌های مارکوف، توزیع نمایی برای مدل‌سازی زمآن‌های بین حالت‌ها استفاده می‌شود. این امر به بهبود دقت مدل‌ها در پیش‌بینی توالی‌های زمانی کمک می‌کند.

مدل‌های گوسی مختلط

در مدل‌های گوسی مختلط (Gaussian Mixture Models) که برای خوشه‌بندی و مدل‌سازی توزیع‌های پیچیده استفاده می‌شوند، توزیع نمایی می‌تواند به عنوان یکی از اجزای توزیع‌های ترکیبی به کار رود، به خصوص در مواردی که فاصله‌های زمانی بین داده‌ها مورد نیاز است.

شبکه‌های عصبی بازگشتی

در شبکه‌های عصبی بازگشتی (Recurrent Neural Networks) که برای پردازش داده‌های سری زمانی و توالی‌ها استفاده می‌شوند، توزیع نمایی می‌تواند برای مدل‌سازی فاصله‌های زمانی بین رویدادها در ورودی‌ها به کار رود، که به بهبود دقت پیش‌بینی‌ها کمک می‌کند.

مدل‌سازی زمان پاسخ در سیستم‌های توصیه‌گر

در سیستم‌های توصیه‌گر (Recommender Systems)، توزیع نمایی می‌تواند برای مدل‌سازی زمان بین تعاملات کاربر و سیستم، مانند کلیک‌ها، خریدها یا بازدیدها، استفاده شود. این امر به بهبود دقت مدل‌های توصیه‌گر و افزایش رضایت کاربران کمک می‌کند.

توزیع تی-استیودنت

توزیع تی-استیودنت (Student’s t-distribution) یکی از توزیع‌های مهم آماری است که برای تحلیل و مدل‌سازی داده‌ها به ویژه در شرایطی که تعداد نمونه‌داده‌ها کوچک است یا واریانس جامعه ناشناخته می‌باشد، استفاده می‌شود. این توزیع به‌ویژه در تحلیل داده‌ها و آزمون‌های فرضیه کاربرد دارد.

ویژگی‌های توزیع تی-استیودنت

درادامه به‌بررسی ویژگی‌های این توزیع آماری می‌پردازیم:

• شکل متقارن: توزیع تی استیودنت مانند توزیع نرمال متقارن است، اما در مقایسه با توزیع نرمال دارای دنباله‌های بلندتر و پهن‌تر می‌باشد. این ویژگی به خصوص در نمونه‌های کوچک‌تر که احتمال وقوع مقادیر دور از میانگین بیشتر است، بسیار مفید است.
• درجه آزادی: با افزایش درجه آزادی (ν)، توزیع تی به توزیع نرمال نزدیک‌تر می‌شود. در واقع، وقتی درجه آزادی به سمت بی‌نهایت می‌رود، توزیع تی به توزیع نرمال استاندارد تبدیل می‌شود.

فرمول ریاضی

تابع چگالی احتمال توزیع تی-استیودنت به شکل زیر است:

\large f(t; \nu) = \frac{\Gamma \left( \frac{\nu + 1}{2} \right)} {\sqrt{\nu \pi} \Gamma \left( \frac{\nu}{2} \right)} \left( 1 + \frac{t^2}{\nu} \right)^{-\frac{\nu + 1}{2}}

در این فرمول:

• t متغیر تصادفی است که توزیع تی استیودنت را دنبال می‌کند.
• ν (نو) درجه‌های آزادی است. درجه آزادی معمولاً به تعداد نمونه‌داده‌ها منهای یک (n-1) اشاره دارد.
• Γ تابع گاما است که تعمیمی از تابع فاکتوریل برای اعداد حقیقی و مختلط است. به عبارت دیگر، برای یک عدد صحیح n داریم: !Γ(n)=(n−1)

ضریب نرمال‌سازی

بخش اول فرمول که شامل نسبت دو تابع گاما و یک عبارت شامل π و ν است، یک ثابت نرمال‌سازی است که تضمین می‌کند مساحت زیر منحنی تابع چگالی احتمال برابر با یک باشد.

بخش توانی

این بخش از فرمول شکل تابع چگالی احتمال را تعیین می‌کند. عبارت t2/ν + 1 بیانگر توزیع تی-استیودنت است که به درجه آزادی (ν) وابسته است. توان 2 /1+ ν- نیز باعث شکل‌گیری دنباله‌های بلندتر و پهن‌تر نسبت به توزیع نرمال می‌شود.

نحوه کارکرد فرمول

وقتی ν بزرگ می‌شود (به سمت بی‌نهایت میل می‌کند)، توزیع تی-استیودنت به توزیع نرمال نزدیک‌تر می‌شود. در نمونه‌های کوچک، توزیع تی به دلیل داشتن دنباله‌های پهن‌تر، احتمال بیشتری به مقادیر دور از میانگین اختصاص می‌دهد. این ویژگی باعث می‌شود که توزیع تی در تحلیل داده‌ها با حجم نمونه کوچک یا واریانس ناشناخته بسیار مفید باشد.

تحلیل نمودار توزیع تی-استیودنت برای درجات آزادی مختلف

برای مشاهده تاثیر درجات آزادی مختلف روی نمودار توزیع تی-استیودنت به شکل زیر توجه کنید:

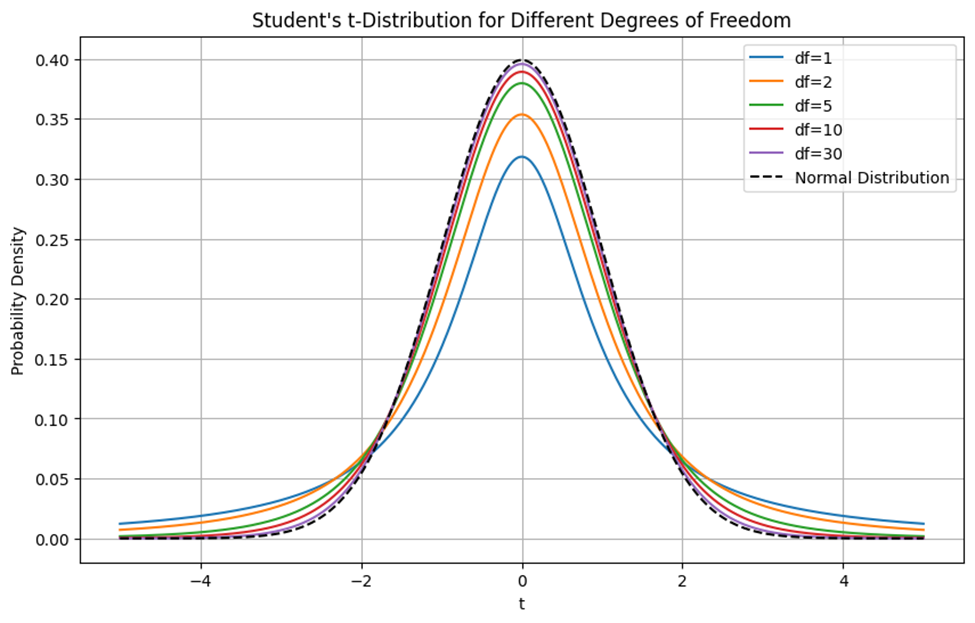
نمودار فوق نمایشگر توزیع تی استیودنت برای درجات آزادی (df) مختلف (۱، ۲، ۵، ۱۰ و ۳۰) است. همچنین، توزیع نرمال استاندارد (Normal Distribution) برای مقایسه به صورت خط‌چین سیاه رنگ نمایش داده شده است.

در درجه آزادی پایین توزیع تی-استیودنت با df=1 دارای دنباله‌های بسیار بلندتری نسبت به توزیع نرمال است. این به معنای احتمال بیشتر برای مشاهده مقادیر دور از میانگین است. در درجات آزادی متوسط مانند df=5، توزیع تی به تدریج به توزیع نرمال نزدیک‌تر می‌شود. البته در این حالت توزیع تی هنوز دنباله‌های بلندتری نسبت به توزیع نرمال دارد، اما این دنباله‌ها از دنباله‌های df=1 کوتاه‌تر هستند. در درجات آزادی بالاتر، مانند df=30، توزیع تی استیودنت بسیار شبیه به توزیع نرمال می‌شود. در این موارد، تفاوت‌ها کمتر قابل مشاهده هستند و دنباله‌ها نیز به توزیع نرمال نزدیک‌تر شده‌اند. همان‌طور که مشخص است، با افزایش درجه آزادی، توزیع تی به تدریج به توزیع نرمال استاندارد نزدیک‌تر می‌شود.

کاربردهای توزیع تی-استیودنت در یادگیری ماشین

توزیع تی-استیودنت در یادگیری ماشین نقش مهمی ایفا می‌کند و در بسیاری از الگوریتم‌ها و مدل‌های مختلف مورد استفاده قرار می‌گیرد. در ادامه به برخی از کاربردهای خاص آن در این حوزه اشاره می‌کنیم:

رگرسیون مقاوم

رگرسیون مقاوم (Robust Regression) یکی از روش‌های مهم در یادگیری ماشین است که به منظور مقابله با نقاط پرت و داده‌های ناهنجار استفاده می‌شود. توزیع تی-استیودنت به دلیل دنباله‌های پهن‌تر و حساسیت کمتر به نقاط پرت، به عنوان تابع خطا در مدل‌های رگرسیون روباست به کار می‌رود. این کاربرد به بهبود دقت مدل در حضور داده‌های ناهنجار کمک می‌کند.

شبکه‌های عصبی بیزی

شبکه‌های عصبی بیزی (Bayesian Neural Networks یا BNNs) نوعی شبکه عصبی هستند که در آن‌ها پارامترهای مدل (مانند وزن‌ها و بایاس‌ها) به صورت توزیع‌های احتمالی مدل‌سازی می‌شوند، نه مقادیر ثابت. این روش به مدل این امکان را می‌دهد تا عدم قطعیت‌ها را در یادگیری و پیش‌بینی‌ها در نظر بگیرد، که می‌تواند در بسیاری از کاربردها مفید باشد. یکی از مفاهیم اصلی در BNNها، توزیع پیشین (Prior Distribution) است که نشان‌دهنده باورهای اولیه در مورد پارامترها قبل از مشاهده داده‌ها است. در این‌جا می‌توان از توزیع تی-استیودنت به عنوان توزیع پیشین برای وزن‌ها استفاده کرد زیرا دارای دم‌های سنگین‌تری نسبت به توزیع نرمال است، که به مدل امکان می‌دهد تا احتمال وقوع وزن‌های بزرگ‌تر را در نظر بگیرد.

این ویژگی باعث می‌شود تا BNNs توانایی بهتری در مواجهه با داده‌های نادر و نویزی داشته باشند. توزیع پسین (Posterior Distribution) از دیگر مفاهیم این حوزه است که پس از مشاهده داده‌ها و به‌روزرسانی باورها، محاسبه می‌شود و نشان‌دهنده باورهای به‌روزرسانی‌شده در مورد پارامترها است.

تحلیل مولفه‌های اصلی

در تحلیل مولفه‌های اصلی (PCA) مقاوم، از توزیع تی-استیودنت برای مدل‌سازی داده‌ها استفاده می‌شود. این امر به ویژه در مواردی که داده‌ها شامل نویز یا نقاط پرت هستند، مفید است. توزیع تی با دنباله‌های پهن‌تر خود، قادر به مدل‌سازی بهتر این نوع داده‌ها می‌باشد.

توزیع فیشر

توزیع فیشر (Fisher Distribution) که بیشتر با نام توزیع اف (F-distribution) شناخته می‌شود، یکی از توزیع‌های مهم و پرکاربرد در آمار و احتمال است. این توزیع به افتخار رونالد فیشر، یکی از پیشگامان علم آمار، نامگذاری شده است.

ویژگی‌های توزیع فیشر

درادامه به‌بررسی ویژگی‌های این توزیع می‌پردازیم:

• عدم تقارن: توزیع اف معمولاً یک توزیع نامتقارن است که دنباله بلندتری در سمت راست دارد.
• وابستگی به درجه‌های آزادی: شکل توزیع اف به شدت به درجه‌های آزادی d1​ و d2​ بستگی دارد. با افزایش درجه آزادی، توزیع اف به سمت توزیع نرمال نزدیک‌تر می‌شود.

فرمول ریاضی

تابع چگالی احتمال توزیع فیشر به شکل زیر است:

\large f(x; d_1, d_2) = \frac{\left( \frac{d_1}{d_2} \right)^{d_1 / 2} x^{(d_1 / 2 - 1)}}{B(d_1 / 2, d_2 / 2) \left( 1 + \frac{d_1}{d_2} x \right)^{(d_1 + d_2) / 2}}

در این فرمول:

• x مقدار متغیر تصادفی است که توزیع اف را دنبال می‌کند.
• d1 ​ و d2 درجات آزادی هستند که به ترتیب مربوط به صورت و مخرج نسبت واریانس‌ها هستند.
• B تابع بتا است که به صورت زیر تعریف می‌شود:

\large B(x, y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x + y)}

• Γ تابع گاما است که برای اعداد صحیح n به صورت !(n−1) تعریف می‌شود و برای مقادیر غیرصحیح با استفاده از یک انتگرال محاسبه می‌شود.

ضریب نرمال‌سازی

بخش اول فرمول که شامل نسبت دو تابع بتا و عبارت (d1/2) (d1/d2) است، به عنوان ضریب نرمال‌سازی عمل می‌کند:

• نسبت درجات آزادی: این عبارت بیانگر نسبت درجات آزادی d₁ و d₂ است که به توان نصف درجه آزادی صورت رسیده است.
• تابع بتا: این تابع که با استفاده از توابع گاما تعریف می‌شود، به نرمال‌سازی چگالی احتمال کمک می‌کند تا مساحت زیر منحنی تابع چگالی احتمال برابر با ۱ باشد.

بخش توانی

بخش توانی این تابع به‌صورت (d1/2 - 1)x تعریف می‌شود که نشان‌دهنده تأثیر درجه آزادی d1​ بر شکل توزیع است. این عبارت باعث می‌شود تابع چگالی احتمال شکل خاصی به خود بگیرد.

عبارت توانی (d1 + d2/2)(1 + d1/d2x) در مخرج کسر نیز نقش مهمی در فرمول ایفا می‌کند. این بخش از فرمول نشان می‌دهد که با افزایش مقدار x، چگونه احتمال کاهش می‌یابد. این عبارت دنباله‌های بلندتری در سمت راست نمودار ایجاد می‌کند که نشان‌دهنده احتمال وقوع مقادیر بزرگ‌تر است.

نحوه کارکرد مدل

با افزایش درجات آزادی، توزیع اف به توزیع نرمال نزدیک‌تر می‌شود. به عبارت دیگر، هرچه درجات آزادی بیشتر باشد، توزیع اف شکل متقارن‌تر و مشابه‌تری به توزیع نرمال خواهد داشت. توزیع اف به دلیل داشتن دنباله‌های بلندتر در سمت راست نمودار، احتمال بیشتری به مقادیر دور از میانگین اختصاص می‌دهد. این ویژگی در تحلیل‌های آماری که نیاز به مقایسه واریانس‌ها دارند، مفید است.

تفسیر نمودار توزیع فیشر با درجات آزادی مختلف

برای مشاهده تاثیر درجات آزادی مختلف روی نمودار توزیع فیشر به شکل زیر توجه کنید:

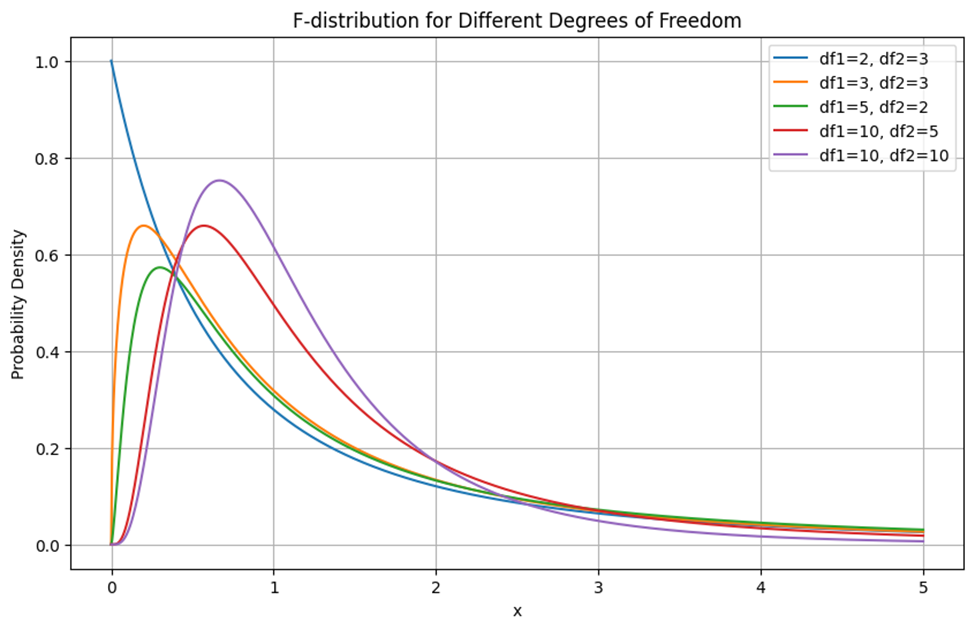
این نمودار توزیع اف (F-distribution) را برای درجات آزادی مختلف d1  و d2 نشان می‌دهد. در درجات آزادی پایین (df1=2, df2=3) نمودار دارای یک قله بسیار تیز و دنباله‌های بلند است. این نشان‌دهنده این است که احتمال وقوع مقادیر بزرگ‌تر از میانگین بیشتر است. در درجه آزادی متوسط (df1=5, df2=2) با افزایش درجات آزادی، قله نمودار کمتر تیز می‌شود و توزیع بیشتر به توزیع نرمال نزدیک می‌شود، اما همچنان دنباله‌ها بلند باقی می‌مانند. درجه آزادی بالا (df1=10, df2=10) توزیع اف به توزیع نرمال کمی نزدیک‌تر می‌شود. قله نمودار پهن‌تر شده و دنباله‌ها کوتاه‌تر می‌شوند، که نشان‌دهنده کاهش احتمال وقوع مقادیر بسیار بزرگ است.

کاربردهای توزیع فیشر در یادگیری ماشین

توزیع فیشر یا توزیع اف یکی از ابزارهای آماری پرکاربرد است که در یادگیری ماشین و تحلیل داده‌ها نقش مهمی ایفا می‌کند. این توزیع به ویژه در آزمون‌های فرضیه و تحلیل واریانس کاربرد دارد که می‌تواند به بهبود مدل‌ها و ارزیابی آن‌ها کمک کند. در ادامه به برخی از کاربردهای اصلی توزیع فیشر در یادگیری ماشین می‌پردازیم.

تحلیل واریانس

یکی از کاربردهای اصلی توزیع اف در یادگیری ماشین، تحلیل واریانس (Analysis of Variance – ANOVA) است. ANOVA برای مقایسه میانگین‌های چند گروه مختلف استفاده می‌شود تا تعیین کند آیا تفاوت‌های مشاهده شده بین میانگین‌ها معنادار هستند یا خیر. ANOVA می‌تواند در یادگیری ماشین برای انتخاب ویژگی‌ها (Feature selections) و تعیین اینکه کدام ویژگی‌ها بیشتر بر روی متغیر وابسته (Label یا Target) تأثیر دارند، استفاده شود.

 ارزیابی مدل‌ها

در یادگیری ماشین، توزیع اف برای ارزیابی مدل‌ها و آزمون معناداری آن‌ها استفاده می‌شود. به عنوان مثال، در رگرسیون چندمتغیره، از توزیع اف برای آزمون معناداری مدل کلی استفاده می‌شود. این آزمون نشان می‌دهد که آیا متغیرهای مستقل به طور جمعی تأثیر معناداری بر متغیر وابسته دارند یا خیر.

انتخاب مدل

توزیع اف در فرآیند انتخاب مدل (Model Selection) نیز کاربرد دارد. یکی از روش‌های انتخاب مدل استفاده از معیارهای اطلاعاتی مانند AIC (Akaike Information Criterion) و BIC (Bayesian Information Criterion) است که به توزیع اف وابسته هستند. این معیارها به انتخاب مدل بهینه با توجه به پیچیدگی و دقت آن کمک می‌کنند.

رگرسیون خطی و لجستیک

در رگرسیون خطی و لجستیک، از توزیع اف برای آزمون معناداری ضرایب رگرسیون استفاده می‌شود. این آزمون‌ها نشان می‌دهند که آیا متغیرهای مستقل به طور معناداری بر متغیر وابسته تأثیر می‌گذارند یا خیر. این کاربرد به بهبود دقت مدل‌ها و انتخاب متغیرهای مهم کمک می‌کند.

تحلیل مؤلفه‌های اصلی

در تحلیل مؤلفه‌های اصلی (PCA)، توزیع اف می‌تواند برای ارزیابی معناداری مؤلفه‌های اصلی استفاده شود. این تحلیل به کاهش ابعاد داده و استخراج ویژگی‌های مهم کمک می‌کند که در بهبود کارایی مدل‌های یادگیری ماشین مؤثر است.

یادگیری تقویتی

در یادگیری تقویتی (Reinforcement Learning)، توزیع داده اف می‌تواند برای ارزیابی سیاست‌ها و الگوریتم‌های یادگیری استفاده شود. این ارزیابی‌ها به تعیین اینکه آیا یک سیاست خاص بهبود یافته است یا خیر و نیز به بهینه‌سازی الگوریتم‌های یادگیری تقویتی کمک می‌کنند.

تحلیل داده‌های زمانی

در تحلیل داده‌های زمانی (Time Series Analysis)، توزیع اف می‌تواند برای مقایسه مدل‌های مختلف پیش‌بینی استفاده شود. این مقایسه‌ها به تعیین مدل بهینه برای پیش‌بینی دقیق‌تر و قابل اعتمادتر کمک می‌کنند.

توزیع گاما

توزیع گاما (Gamma Distribution) یکی از توزیع‌های پیوسته است که برای مدل‌سازی زمان بین رخدادها در فرآیندهای تصادفی، به ویژه در مدل‌های بقا و تحلیل زمان خرابی سیستم‌ها، به کار می‌رود. این توزیع به دلیل انعطاف‌پذیری و توانایی مدل‌سازی داده‌های پراکنده و نامتقارن، در بسیاری از حوزه‌های علمی و مهندسی کاربرد دارد.

ویژگی‌های توزیع گاما

• پیوستگی: توزیع گاما یک توزیع پیوسته است که می‌تواند هر مقدار مثبتی را بگیرد.
• عدم تقارن: این توزیع به خصوص در مقادیر پایین پارامترهایش، معمولاً نامتقارن است اما با افزایش این پارامترها به سمت تقارن میل می‌کند.
• پارامترها: توزیع گاما با دو پارامتر α یا پارامتر شکل و β یا پارامتر مقیاس تعریف می‌شود.

فرمول ریاضی

تابع چگالی احتمال توزیع گاما به صورت زیر است:

\large \begin{cases} \frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x} & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}

در این فرمول:

• پارامتر α که به آن پارامتر شکل نیز می‌گویند، تعیین‌کننده تعداد رخدادها در واحد زمان است. هر چه مقدار α بیشتر باشد، توزیع به سمت توزیع نرمال نزدیک‌تر می‌شود.
• پارامتر β که به آن پارامتر مقیاس نیز می‌گویند، تعیین‌کننده پراکندگی داده‌ها است. هرچه β کوچکتر باشد، پراکندگی داده‌ها بیشتر خواهد بود.
• تابع گاما نیز مطابق همان تعریفی که در قسمت‌های قبل ارائه کردیم، تعمیمی از تابع فاکتوریل است.

ضریب نرمال‌سازی

ضریب (α)βα/Γ اطمینان می‌دهد که مساحت زیر منحنی چگالی احتمال برابر با ۱ باشد.

بخش توانی

این بخش از فرمول نشان‌دهنده تأثیر پارامتر α بر شکل توزیع است:

• اگر α>1 باشد، xα-1 برای مقادیر کوچک x (نزدیک به صفر) مقدار کمی دارد و با افزایش x، افزایش می‌یابد.
• اگر α=1  باشد، x0 بخش توانی تبدیل به  می‌شود که برابر با ۱ است و بنابراین توزیع گاما به یک توزیع نمایی ساده تبدیل می‌شود.
• اگر  α<1 باشد، xα-1 برای مقادیر کوچک x مقدار بزرگی دارد و با افزایش x، کاهش می‌یابد.

اثر پارامتر آلفا بر شکل توزیع

• وقتی α افزایش می‌یابد، توزیع به سمت راست کشیده می‌شود و پهن‌تر می‌شود. به عبارت دیگر، با افزایش α، چگالی توزیع گاما در مقادیر بزرگتر x متمرکز می‌شود.
• وقتی α کاهش می‌یابد، توزیع به سمت چپ متمایل می‌شود و مقدار بیشتری از چگالی در مقادیر کوچک x متمرکز می‌شود.

قسمت نمایی

قسمت e-βx نشان‌دهنده نرخ کاهش چگالی احتمال با افزایش x است. این بخش به صورت نمایی منفی است و باعث می‌شود که چگالی احتمال به سرعت با افزایش x کاهش یابد.

تفسیر نمودار توزیع گاما با پارامترهای مختلف

برای مشاهده تاثیر پارامترهای مختلف روی نمودار توزیع گاما به شکل زیر توجه کنید:

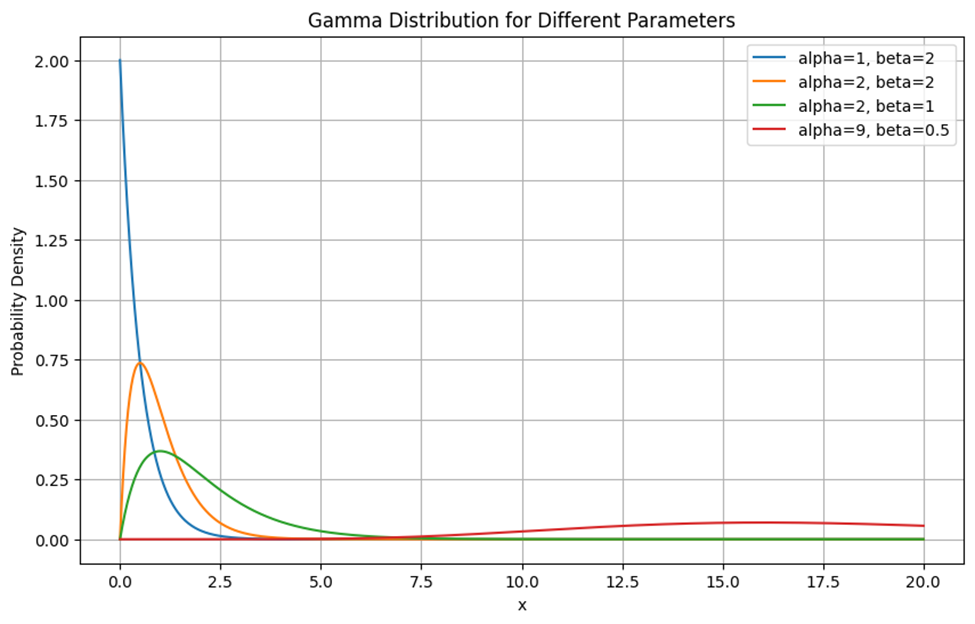
همان‌طور که درشکل می‌بینید، منحنی آبی نشان‌دهنده توزیع گاما با α=1 و β=2 است و چون α=1 است، این توزیع به توزیع نمایی تبدیل می‌شود. پیک یا نقطه اوج این توزیع در x=0 قرار دارد و به سرعت با افزایش x کاهش می‌یابد.

همان‌طور که منحنی نارنجی نشان می‌دهد (alpha=2, beta=2) افزایش α باعث می‌شود که توزیع در مقادیر بزرگتر x متمرکز شود. باتوجه به منحنی سبز رنگ (alpha=2, beta=1)، می‌فهمیم که توزیع گاما با کاهش مقیاس گسترده‌تر می‌شود و پیک آن به‌سمت راست منتقل شود. این توزیع در مقایسه با منحنی نارنجی کشیده‌تر است و پیک آن در مقدار بزرگتری از x قرار دارد. منحنی قرمز نیز نشان‌دهنده توزیع گاما با alpha=9 و beta=0.5 است. این شکل نشان می‌دهد، باافزایش α و کاهش β پیک این توزیع در مقدار x بزرگتری قرار می‌گیرد و توزیع در بازه وسیع‌تری از مقادیر x گسترده می‌شود.

کاربردهای توزیع گاما در یادگیری ماشین

توزیع داده گاما به دلیل انعطاف‌پذیری و توانایی در مدل‌سازی داده‌های دارای چولگی و پیوسته مثبت، یکی از ابزارهای مفید در یادگیری ماشین است. فهم دقیق این توزیع و نحوه استفاده از آن می‌تواند به بهبود مدل‌ها و تحلیل‌های آماری در مسائل مختلف کمک کند. درادامه کاربردهای این توزیع در یادگیری ماشین را بررسی می‌کنیم:

رگرسیون

در برخی مسائل رگرسیون، خصوصاً زمانی که متغیر پاسخ یک مقدار پیوسته و مثبت دارد، توزیع گاما می‌تواند مدل مناسبی باشد. برای مثال، در مدل‌های رگرسیون گاما، متغیر پاسخ با استفاده از تابع پیوند گاما به متغیرهای مستقل مرتبط می‌شود.

استنتاج بیزی

استنتاج بیزی (Bayesian Inference) روشی است برای به‌روز‌رسانی باورها در مورد پارامترهای مدل با توجه به داده‌های مشاهده‌شده. در این روش، از توزیع‌های احتمالی برای بیان عدم قطعیت‌ها در پارامترها استفاده می‌شود. یکی از توزیع‌هایی که در استنتاج بیزی کاربرد فراوان دارد، توزیع گاما است.

مدل‌های پیش‌بینی خطر

توزیع داده گاما در مدل‌های پیش‌بینی خطر برای تخمین زمان وقوع خطرات و حوادث مختلف استفاده می‌شود. این مدل‌ها می‌توانند به شناسایی نقاط بحرانی و پیشگیری از وقوع حوادث کمک کنند.

توزیع کای-دو

توزیع کای-دو (Chi-Square Distribution) یکی از توزیع‌های پیوسته است که از مجموع مربعات k متغیر تصادفی نرمال استاندارد به دست می‌آید. این توزیع در آزمون‌های فرضیه آماری، به ویژه در آزمون‌های مستقل بودن و نیکویی برازش (Goodness of Fit) بسیار کاربرد دارد. توزیع کای-دو زمانی به کار می‌رود که بخواهیم تعداد وقوعات مختلف را با توزیع مورد انتظار مقایسه کنیم. این توزیع در تحلیل داده‌ها و آزمون‌های آماری نقش مهمی ایفا می‌کند.

ویژگی‌های توزیع کای-دو

• پیوستگی: توزیع کای-دو یک توزیع پیوسته است که فقط مقادیر غیرمنفی را می‌پذیرد.
• وابستگی به درجه آزادی: این توزیع به شدت به درجه آزادی k وابسته است. هر چه درجه آزادی بیشتر باشد، توزیع به سمت تقارن میل می‌کند. درجه آزادی نشان‌دهنده تعداد متغیرهای مستقل در تحلیل داده‌ها است.
• عدم تقارن: در درجات آزادی پایین، توزیع کای-دو نامتقارن است، اما با افزایش درجه آزادی به سمت توزیع نرمال میل می‌کند. این عدم تقارن نشان‌دهنده تفاوت در پراکندگی داده‌ها است.

فرمول ریاضی

تابع چگالی احتمال توزیع کای-دو به صورت زیر است:

\large \begin{cases} \frac{1}{2^{k/2}\Gamma(k/2)} x^{(k/2)-1} e^{-x/2} & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}

در این فرمول:

• پارامتر k درجه آزادی و تعیین‌کننده تعداد متغیرهای نرمال استاندارد است که مربعات آن‌ها جمع شده‌اند. به طور کلی، درجه آزادی تعداد متغیرهای مستقل در یک مجموعه داده است. این پارامتر تأثیر مستقیمی بر شکل توزیع دارد.

ضریب نرمال‌سازی

ضریب (k/2)2k/2 Γ در مخرج کسر، اطمینان می‌دهد که مساحت زیر منحنی چگالی احتمال برابر با ۱ باشد. این ضریب ترکیبی از ثابت‌های ریاضی است که توزیع را نرمال می‌کند.

بخش توانی

بخش x(k/2)-1 از فرمول تعیین‌کننده شکل توزیع بر اساس درجه آزادی است. این بخش نشان‌دهنده تأثیر توان x بر چگالی احتمال است.

قسمت نمایی

قسمت نمایی این تابع، نرخ کاهش چگالی احتمال با افزایش x را نشان می‌دهد. این بخش باعث می‌شود که چگالی احتمال باافزایش x سریعا کاهش یابد.

رسم توزیع کای-دو برای پارامترهای مختلف

برای مشاهده تاثیر پارامترهای مختلف روی نمودار توزیع کای-دو به شکل زیر توجه کنید:

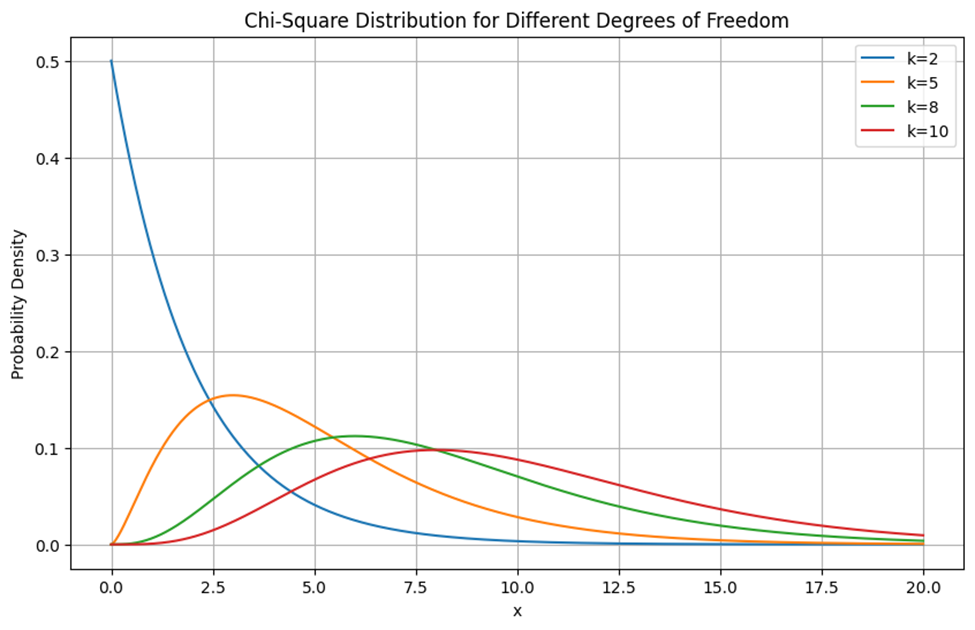
باتوجه به نمودار بالا درمی‌یابیم که در درجات آزادی پایین (k=2) توزیع بسیار تیز و متمرکز در مقادیر پایین است. در درجات آزادی متوسط (k=8) توزیع پهن‌تر شده و مقادیر بالاتری را پوشش می‌دهد. در درجات آزادی بالا (k=10) توزیع به سمت نرمال شدن میل می‌کند و پراکندگی داده‌ها بیشتر می‌شود.

کاربردهای توزیع کای-دو در یادگیری ماشین

توزیع کای-دو (Chi-Square) یکی از توزیع‌های آماری مهم است که کاربردهای متعددی در یادگیری ماشین دارد. در ادامه به بررسی برخی از این کاربردها و ارتباط آن‌ها با توزیع کای-دو می‌پردازیم:

 انتخاب ویژگی

در انتخاب ویژگی (Feature Selection)، هدف شناسایی ویژگی‌های مهم و تاثیرگذار در مدل است. آزمون کای-دو (Chi-Square Test) یکی از آزمون‌های آماری پرکاربرد است که برای بررسی وابستگی و همبستگی بین دو یا چند متغیر دسته‌ای (Categorical Variables) استفاده می‌شود درواقع در تست کای-دو برای انتخاب ویژگی‌ها از توزیع کای-دو برای محاسبه آماره استفاده می‌کند. اگر مقدار آماره کای-دو محاسبه‌شده برای یک ویژگی بزرگ باشد، به این معناست که این ویژگی با خروجی هدف (label) ارتباط قوی دارد و بنابراین می‌تواند به عنوان یک ویژگی مهم در نظر گرفته شود.

تحلیل خوشه‌بندی

خوشه‌بندی فرآیندی است که در آن داده‌ها به گروه‌هایی تقسیم می‌شوند به طوری که داده‌های داخل هر گروه (خوشه) به یکدیگر شباهت بیشتری دارند و از داده‌های گروه‌های دیگر متفاوت هستند. برای ارزیابی کیفیت این خوشه‌بندی، می‌توان از تست کای-دو استفاده کرد تا تعیین شود که آیا خوشه‌های شناسایی شده به طور معناداری از هم متمایز هستند یا خیر. به‌این‌صورت که مقدار آماره کای-دو با مقدار بحرانی (critical value) از جدول توزیع کای-دو مقایسه می‌شود که این مقدار بحرانی بر اساس سطح معناداری (significance level) و درجه آزادی (degrees of freedom) تعیین می‌شود. اگر مقدار آماره کای-دو بزرگتر از مقدار بحرانی باشد، به‌این معنا است که خوشه‌ها به‌خوبی از هم متمایز هستند.

تشخیص ناهنجاری‌ها

در تشخیص ناهنجاری‌ها (Anomaly Detection)، توزیع کای-دو می‌تواند برای شناسایی نقاط داده‌ای که به طور معناداری از دیگر داده‌ها متفاوت هستند، استفاده شود. به‌این‌صورت که نقاطی که دارای آماره کای-دو بالایی هستند، به عنوان ناهنجاری شناسایی می‌شوند.

توزیع لاپلاس

توزیع لاپلاس (Laplace Distribution) که به عنوان توزیع دو نمایی نیز شناخته می‌شود، یک توزیع پیوسته است که برای مدل‌سازی داده‌هایی که تغییرات ناگهانی و پراکندگی بالا دارند، مفید است. این توزیع دارای یک نقطه مرکزی است که داده‌ها حول آن متمرکز شده و دنباله‌های نمایی در دو طرف دارد. توزیع لاپلاس می‌تواند برای مدل‌سازی داده‌هایی که دارای تغییرات ناگهانی و شدید هستند، مناسب باشد.

ویژگی‌های توزیع لاپلاس

• تقارن: توزیع لاپلاس یک توزیع پیوسته است که حول میانگین خود متقارن است. تقارن توزیع لاپلاس به معنی این است که احتمال وقوع داده‌ها در دو سمت میانگین یکسان است.
• دنباله‌های بلند: این توزیع دنباله‌های بلندتری نسبت به توزیع نرمال دارد که نشان‌دهنده احتمال بالاتر وقوع مقادیر دور از میانگین است. این ویژگی باعث می‌شود که توزیع لاپلاس برای مدل‌سازی داده‌های دارای نقاط پرت مناسب باشد.

فرمول ریاضی

تابع چگالی احتمال توزیع لاپلاس به صورت زیر است:

\large f(x \mid \mu, b) = \frac{1}{2b} \exp \left( -\frac{|x - \mu|}{b} \right)

در این فرمول:

• μ پارامتر میانگین است که مرکز تقارن توزیع را تعیین می‌کند. این پارامتر نشان‌دهنده نقطه‌ای است که داده‌ها حول آن متمرکز شده‌اند.
• b پارامتر مقیاس توزیع است که میزان پراکندگی داده‌ها را تعیین می‌کند. هرچه مقدار b بیشتر باشد، پراکندگی داده‌ها بیشتر خواهد بود.

ضریب نرمال‌سازی

ضریب 1/2b کاری می‌کند که مساحت زیر منحنی چگالی احتمال برابر با ۱ باشد و باعث نرمال شدن توزیع می‌شود.

بخش نمایی

این بخش نشان‌دهنده نحوه کاهش مقدار چگالی احتمال با فاصله گرفتن از میانگین است که به صورت نمایی منفی است و باعث می‌شود که چگالی احتمال با افزایش فاصله از میانگین کاهش یابد.

رسم توزیع لاپلاس برای پارامترهای مختلف

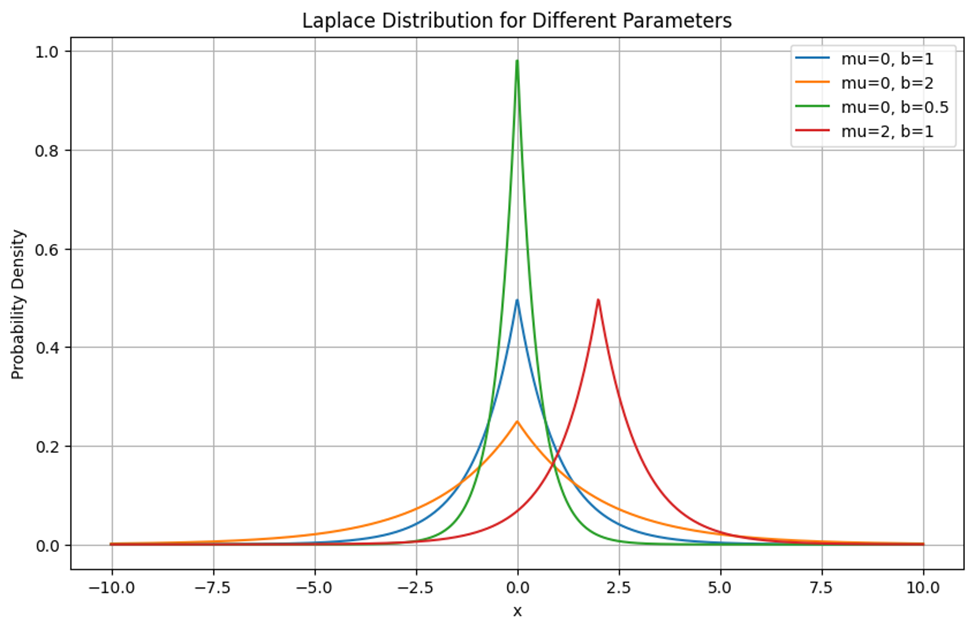
این نمودار توابع چگالی احتمال توزیع لاپلاس را برای مجموعه‌ای از پارامترهای مختلف μ (میانگین) و b (مقیاس) نشان می‌دهد. توزیع لاپلاس که به عنوان توزیع دوقلو-نمایی نیز شناخته می‌شود، دارای یک قله در نقطه پارامتر میانگین و دنباله‌هایی است که به صورت نمایی کاهش می‌یابند.

همان‌طور که در شکل پیدا است، خط آبی نشان‌دهنده توزیع لاپلاس با میانگین صفر و مقیاس یک است. این توزیع در نقطه x=0 دارای پیک (Peak) است و به سرعت به سمت راست و چپ کاهش می‌یابد. در این شکل پراکندگی داده‌ها متوسط است و دنباله‌های نمایی در دو طرف وجود دارد.

خط نارنجی نشان‌دهنده توزیع لاپلاس با میانگین صفر و مقیاس ۲ (بیشتر از مقیاس خط آبی) است. به‌همین دلیل نسبت به خط آبی، قله توزیع کمتر تیز است و پراکندگی داده‌ها بیشتر است. همچنین توزیع به سمت مقادیر دورتر کشیده‌تر شده و دنباله‌های بلندتری دارد.

خط سبز، نشان‌دهنده توزیع لاپلاس با میانگین صفر و مقیاس ۰.۵ (کمتر از مقیاس خط آبی) است. به‌همین دلیل قله توزیع تیزتر از خط آبی است و پراکندگی داده‌هایش از آن کمتر است. همچنین توزیع به سرعت در دو طرف کاهش می‌یابد و دنباله‌های کوتاه‌تری دارد.

خط قرمزرنگ نشان‌دهنده توزیع لاپلاس با میانگین۲ و مقیاس ۱ است. برای همین پیک توزیع در نقطه x=2 است و به سرعت به سمت راست و چپ کاهش می‌یابد.

به‌طور کلی پارارمتر میانگین مرکز توزیع را جابه‌جا می‌کند. برای مثال در این شکل، خطوط آبی، نارنجی و سبز در x=0 متمرکز هستند، در حالی که خط قرمز در x=2 متمرکز است. پارامتر b پهنای توزیع را کنترل می‌کند. هرچه این پارامتر کوچکتر باشد، توزیع باریک‌تر و قله بلندتر می‌شود.

کاربردهای توزیع لاپلاسی در یادگیری ماشین

در ادامه کاربردهای این توزیع را بررسی می‌کنیم:

تنظیم مدل‌ها

تابع هزینه‌ای که برای جریمه L1 Regularizatio استفاده می‌شود، معادل تابع احتمال توزیع لاپلاس است. در این نوع تنظیم، هدف کاهش تعداد ویژگی‌های (Features) غیرصفر مدل است. به عبارت دیگر، افزودن یک جریمه L1  به تابع هزینه معادل فرض کردن توزیع لاپلاس برای پارامترها است که باعث می‌شود بسیاری از پارامترها به صفر نزدیک شوند. جریمه L1 تمایل دارد تا وزن‌ فیچرهای کم اهمیت را به صفر نزدیک کند و از این طریق مدل‌های ساده‌تر و قابل تفسیرتر بسازد.

مدل‌های لاپلاسی

در پردازش زبان طبیعی (NLP) و به‌خصوص در مدل‌های احتمالاتی مانند مدل‌های نایوبیز، هموارسازی لاپلاسی (Laplace Smoothing) به کار می‌رود. این تکنیک شامل اضافه کردن یک ثابت به تعداد کلمات است تا از مشکل تقسیم بر صفر جلوگیری شود و همچنین احتمال کلمات نادیده گرفته شده را به طور غیر صفر تخمین بزند.

مدل‌های رگرسیون

در مدل‌های رگرسیون، هدف پیش‌بینی مقدار یک متغیر وابسته (dependent variable) بر اساس یک یا چند متغیر مستقل (independent variables) است. برای ارزیابی معناداربودن متغیرهای مستقل، از آزمون‌های آماری استفاده می‌شود. یکی از این آزمون‌ها، آزمون کای-دو است. نحوه عملکرد آزمون کای-دو در مدل‌های رگرسیون به‌این‌صورت است که یک مدل رگرسیون لجستیک یا رگرسیون خطی با متغیر وابسته و یک یا چند متغیر مستقل ساخته می‌شود. سپس آماره کای-دو برای هر متغیر مستقل محاسبه می‌شود. در مدل‌های رگرسیون لجستیک، آماره کای-دو از تفاضل دو مدل محاسبه می‌شود: مدلی که شامل متغیر مستقل مورد نظر است و مدلی که شامل آن متغیر نیست. این آماره به عنوان مقدار احتمالی (p-value) ارزیابی می‌شود. اگر مقدار p-value کوچکتر از سطح معناداری (معمولاً ۰.۰۵) باشد، نتیجه می‌گیریم که متغیر مستقل به طور معناداری بر متغیر وابسته تأثیر دارد. در غیر این صورت، متغیر مستقل تأثیر معناداری ندارد.

توزیع لجستیک

توزیع لجستیک یک توزیع پیوسته است که برای مدل‌سازی متغیرهای وابسته باینری و داده‌هایی که تغییرات سریعی دارند، به کار می‌رود. این توزیع در بسیاری از مدل‌های رگرسیون لجستیک و شبکه‌های عصبی کاربرد دارد.

ویژگی‌های توزیع لجستیک

• تقارن: توزیع لجستیک یک توزیع پیوسته است که حول میانگین خود متقارن است.
• دنباله‌های بلند: این توزیع دنباله‌های بلندتری نسبت به توزیع نرمال دارد که نشان‌دهنده احتمال بالاتر وقوع مقادیر دور از میانگین است.

فرمول ریاضی

تابع چگالی احتمال توزیع لجستیک به صورت زیر است:

\large f(x; \mu, s) = \frac{e^{-(x-\mu)/s}}{s \left(1 + e^{-(x-\mu)/s}\right)^2}

در این فرمول:

• μ پارامتر میانگین یا مکان توزیع است که مرکز تقارن توزیع را تعیین می‌کند. این پارامتر نشان‌دهنده نقطه‌ای است که داده‌ها حول آن متمرکز شده‌اند.
• s پارامتر مقیاس توزیع است که میزان پراکندگی داده‌ها را تعیین می‌کند. هرچه مقدار s بیشتر باشد، پراکندگی داده‌ها بیشتر خواهد بود.

ضریب نرمال‌سازی

s در مخرج کسر، تضمین می‌کند که مساحت زیر منحنی چگالی احتمال برابر با ۱ باشد. این ضریب باعث نرمال شدن توزیع می‌شود.

بخش نمایی

این بخش نشان‌دهنده نحوه کاهش مقدار چگالی احتمال با فاصله گرفتن از میانگین است. این بخش به صورت نمایی منفی است و باعث می‌شود که چگالی احتمال به‌سرعت با افزایش فاصله از میانگین کاهش یابد.

رسم توزیع لجستیک برای پارامترهای مختلف

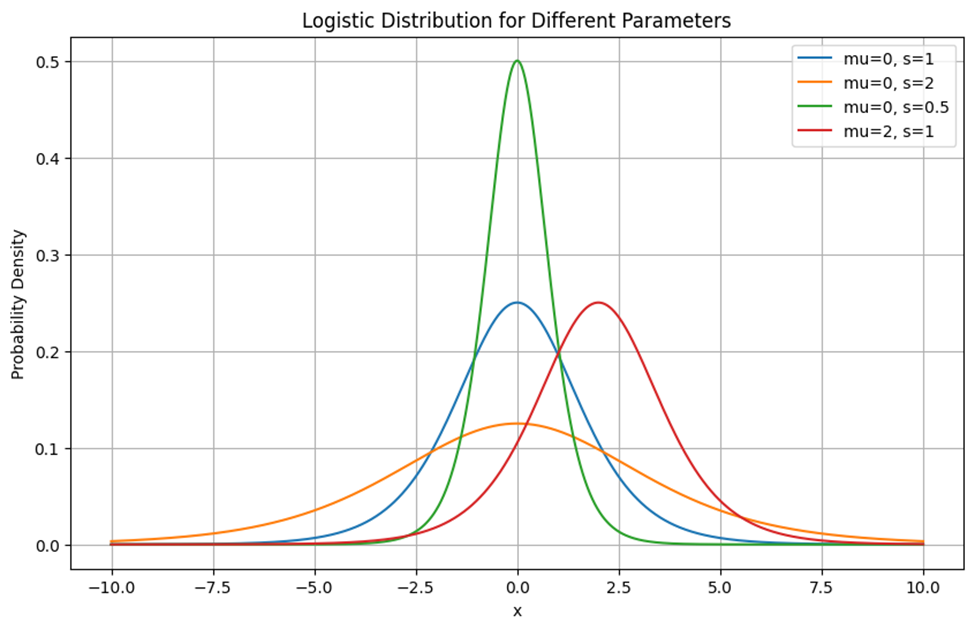
این نمودار توزیع لجستیک برای پارامترهای مختلف را نشان می‌دهد. این نمودار نشان می‌دهد که هرچه مقدار s  بیشتر باشد، منحنی پهن‌تر و مسطح‌تر می‌شود و هرچه مقدار s کمتر باشد، منحنی باریک‌تر و نقطه اوج آن تیزتر می‌شود. همچنین، تغییر مقدار μ باعث جابجایی منحنی به سمت چپ یا راست می‌شود. به عنوان مثال، منحنی سبز (μ=0, s=0.5) نسبت به منحنی آبی (μ=0, s=1) باریک‌تر و قله آن بلندتر است، در حالی که منحنی نارنجی (μ=0, s=2) پهن‌تر و مسطح‌تر است. منحنی قرمز (μ=2, s=1) هم نسبت به منحنی آبی به سمت راست جابجا شده است.

کاربردهای توزیع لجستیک در یادگیری ماشین

توزیع لجستیک به دلیل ویژگی‌های منحصر به فرد خود در برخی از الگوریتم‌ها و مدل‌های یادگیری ماشین به کار گرفته می‌شود. درادامه به‌بررسی آن‌ها می‌پردازیم:

 مدل‌های مخفی مارکوف

در مدل‌های مخفی مارکوف (Hidden Markov Models)، توزیع لجستیک نقش مهمی در مدل‌سازی احتمالات انتقال حالت‌ها و توزیع احتمالات خروجی‌ها ایفا می‌کند. مدل‌های مخفی مارکوف برای مدل‌سازی دنباله‌هایی از مشاهدات که به صورت تصادفی ایجاد شده‌اند، استفاده می‌شوند. در این مدل‌ها، حالت‌های سیستم ناشناخته یا مخفی (Hidden) هستند و تنها مشاهدات قابل دسترسی هستند. توزیع لجستیک می‌تواند برای مدل‌سازی احتمال انتقال از یک حالت مخفی به حالت دیگر استفاده شود. به این ترتیب، برای هر جفت حالت مخفی، یک تابع لجستیک تعیین می‌شود که احتمال انتقال بین آن‌ها را مدل‌سازی می‌کند.

در مدل‌های مخفی مارکوف، احتمالات انتقال به معنای احتمال حرکت از یک حالت مخفی به حالت مخفی دیگر است. این احتمالات تعیین می‌کنند که سیستم با چه احتمالی از یک حالت فعلی به حالت جدیدی منتقل می‌شود. توزیع لجستیک برای مدل‌سازی احتمال تولید یک مشاهده خاص از یک حالت مخفی خاص نیز استفاده می‌شود. احتمالات خروجی در HMM به معنای احتمال تولید یک مشاهده خاص در یک حالت مخفی مشخص است. این احتمالات مشخص می‌کنند که در هر حالت مخفی چه نوع مشاهداتی با چه احتمالاتی ممکن است رخ دهند.

 مدل‌های رگرسیونی تعمیم‌یافته

در مدل‌های رگرسیونی تعمیم یافته (Generalized Linear Models)، توزیع داده لجستیک به عنوان یک تابع لینک برای مدل‌سازی انواع مختلف داده‌ها به کار می‌رود. GLMها یک چارچوب جامع برای مدل‌سازی رابطه بین یک یا چند متغیر مستقل (پیش‌بینی‌کننده‌ها) و یک متغیر وابسته (پاسخ) ارائه می‌دهند. این مدل‌ها توسعه‌ای از رگرسیون خطی ساده هستند و امکان مدل‌سازی داده‌هایی با توزیع‌های مختلف را فراهم می‌کنند. توزیع لجستیک به عنوان تابع لینک در GLM به‌کار می‌رود تا رابطه بین متغیرهای پیش‌بینی‌کننده و متغیر پاسخ را مدل‌سازی کند. تابع لینک، تابعی است که میانگین تابع پاسخ را به ترکیب خطی پیش‌بینی‌کننده‌ها متصل می‌کند. این تابع لینک به تبدیل مقادیر پیش‌بینی شده به دامنه مناسب (مثل ۰ تا ۱ برای احتمالات) کمک می‌کند.

 روش‌های بیزی

در روش‌های بیزی، توزیع لجستیک به عنوان یک تابع احتمال پیشین برای پارامترهای مدل به کار می‌رود. برای نمونه توزیع لجستیک می‌تواند به عنوان توزیع پیشین برای وزن‌های شبکه‌های عصبی یا سایر مدل‌های رگرسیونی استفاده شود. این توزیع به مدل اجازه می‌دهد تا باورهای اولیه در مورد وزن‌ها را به صورت احتمالاتی بیان کند.

توزیع بتا

توزیع بتا (Beta Distribution) یکی از توزیع‌های پیوسته احتمالی است که در بسیاری از کاربردهای آماری و مدل‌سازی مورد استفاده قرار می‌گیرد. این توزیع به خصوص در مواردی مفید است که بخواهیم احتمال وقوع یک رخداد را در یک بازه محدود (معمولاً بین صفر و یک) بررسی کنیم.

ویژگی‌های توزیع بتا

• محدود به بازه ۰ و ۱: توزیع بتا یک توزیع پیوسته است که مقادیر بین ۰ و ۱ را می‌پذیرد.
• انعطاف‌پذیری: توزیع بتا با تغییر پارامترهای خود می‌تواند شکل‌های مختلفی به خود بگیرد. این ویژگی باعث می‌شود که توزیع بتا در بسیاری از موارد کاربرد داشته باشد.

فرمول ریاضی

فرمول چگالی احتمال توزیع بتا به‌صورت زیر است:

\large f(x; \alpha, \beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha - 1} (1 - x)^{\beta - 1}

در این فرمول:

•  α پارامتر شکل است که میزان کشیدگی توزیع در سمت چپ را تعیین می‌کند. هرچه مقدار  بیشتر باشد، توزیع به سمت راست کشیده‌تر می‌شود.
• β پارامتر شکل است که میزان کشیدگی توزیع در سمت راست را تعیین می‌کند. هرچه مقدار  بیشتر باشد، توزیع به سمت چپ کشیده‌تر می‌شود.

ضریب نرمال‌سازی

این ضریب که ترکیبی از توابع گاما است، باعث می‌شود که مساحت زیر منحنی چگالی احتمال در بازه صفر تا یک برابر با ۱ باشد. این ضریب ترکیبی از ثابت‌های ریاضی است که توزیع را نرمال می‌کند.

بخش‌های توانی

بخش xα-1 نشان‌دهنده شکل توزیع در نزدیکی x=0 است. اگر 1<α باشد تابع در این نقطه (x=0) به سمت صفر میل می‌کند. اگر 1>α باشد، تابع در این نقطه به سمت بی‌نهایت میل می‌کند. اگر 0=α باشد، این بخش به ثابت یک تبدیل می‌شود.
بخش (β-1)(1-x) شکل توزیع در نزدیکی x=1 را مشخص می‌کند. اگر 1<β باشد تابع در این نقطه (x=1) به سمت صفر میل می‌کند. اگر 1>β باشد، تابع در این نقطه به سمت بی‌نهایت میل می‌کند. اگر β=0 باشد، این بخش به ثابت یک تبدیل می‌شود.

رسم توزیع بتا برای پارامترهای مختلف

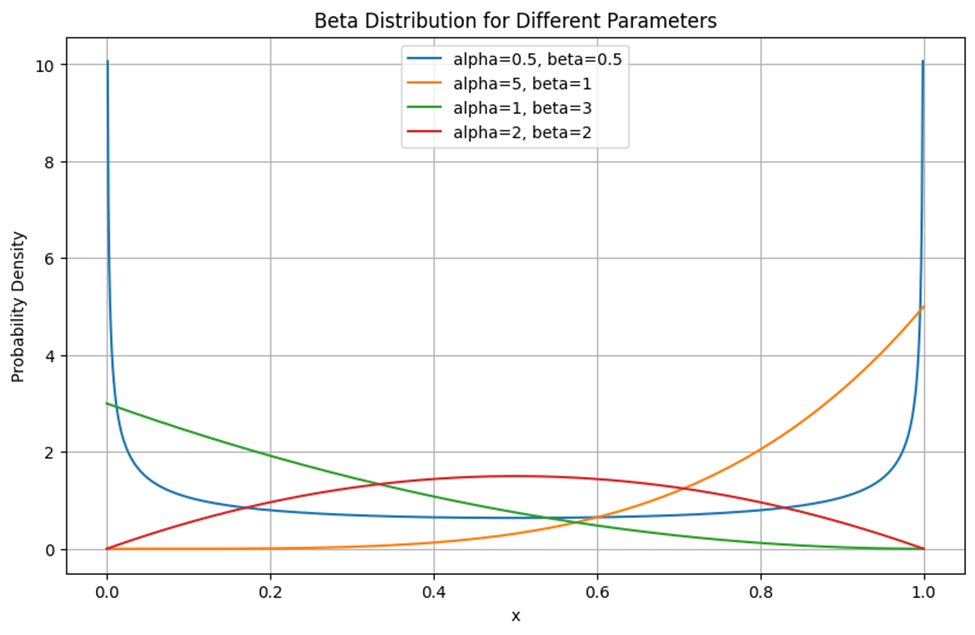
این نمودار تابع چگالی احتمال توزیع بتا را برای مقادیر مختلف پارامترهای شکل α و β نشان می‌دهد. خط آبی با آلفا و بتای کمتر از یک، در نزدیکی نقاط ۰ و ۱ بیشترین مقدار را دارد و در نقاط میانی به حداقل مقدار خود می‌رسد. خط نارنجی، با α=5 (بیشتر از α خط آبی) در نزدیکی نقطه یک اوج می‌گیرد. خط سبز برعکس خط نارنجی، نشان‌دهنده یک توزیع بتا با آلفای برابر ۱ و بتای بزرگتر در نزدیکی نقطه صفر بیشترین مقدار را دارد و به تدریج با نزدیک شدن به نقطه یک، کم شده و به صفر میل می‌کند. خط قرمز (β=2 ,α=2) نشان‌دهنده یک توزیع بتا متقارن با پارارمترهای شکل برابر است. این توزیع در وسط دامنه خود، یعنی در x=0.5، بیشترین مقدار را دارد.

به‌طور کلی این نمودار نشان می‌دهد که با تغییر پارامترهای α و β شکل توزیع بتا چگونه تغییر می‌کند. مقادیر مختلف این پارامترها می‌توانند باعث شوند که توزیع در نزدیکی نقاط صفر، یک یا وسط دامنه اوج بگیرد و به نحوی چگالی احتمال را در طول دامنه تغییر دهند.

کاربردهای توزیع بتا در یادگیری ماشین

این توزیع در حوزه یادگیری ماشین به‌شرح زیر قابل استفاده است:

مدل‌های رگرسیون بتا

مدل‌های رگرسیون بتا (Beta Regression Models) برای مسائل رگرسیون طراحی شده‌اند که در آن‌ها متغیر پاسخ یک مقدار بین صفر و یک دارد. این مدل‌ها برای پیش‌بینی داده‌هایی که به صورت نسبت یا احتمال بیان می‌شوند، بسیار مناسب هستند. مثال‌های معمول این مدل‌ها شامل پیش‌بینی نرخ‌های تبدیل در بازاریابی دیجیتال، نرخ خطا در سیستم‌های تشخیص و درصد رشد در بیومتریک‌ها هستند.

یادگیری فعال

یادگیری فعال (Active Learning) رویکردی در یادگیری ماشین است که هدف آن کاهش تعداد نمونه‌های برچسب‌دار مورد نیاز برای آموزش مدل‌های دقیق است. در این رویکرد، مدل به طور فعال نمونه‌هایی را انتخاب می‌کند که باید برچسب‌گذاری شوند تا یادگیری بهینه انجام شود. در یادگیری فعال، توزیع بتا می‌تواند برای مدل‌سازی عدم قطعیت در پیش‌بینی‌ها استفاده شود. به عنوان مثال، اگر مدل به جای ارائه یک پیش‌بینی قطعی، احتمالات را بر اساس توزیع بتا گزارش دهد، می‌توان از این اطلاعات برای انتخاب نمونه‌های جدید برای برچسب‌گذاری استفاده کرد.

مدل‌های آمیخته بتا

در مسائل خوشه‌بندی و دسته‌بندی داده‌هایی که نسبت‌ها یا احتمالات بین صفر و یک هستند، از مدل‌های آمیخته بتا (Beta Mixture Models) استفاده می‌شود. این مدل‌ها برای تحلیل خوشه‌بندی (clustering) و دسته‌بندی (classification) داده‌های احتمالی یا نسبتی مناسب هستند. در این مدل‌ها، هر زیرگروه توسط یک توزیع بتا مدل‌سازی می‌شود و توزیع کلی داده‌ها به عنوان ترکیبی از این توزیع‌ها بیان می‌شود.

توزیع رایلی

توزیع رایلی (Rayleigh Distribution) یک توزیع پیوسته است که برای مدل‌سازی داده‌هایی که دارای بردارهای دوبعدی با مولفه‌های مستقل نرمال استاندارد هستند، استفاده می‌شود. توزیع رایلی به دلیل توانایی مدل‌سازی داده‌های دوبعدی با مولفه‌های مستقل، می‌تواند برای تحلیل داده‌های مهندسی و ارتباطات مفید باشد.

فرمول ریاضی

تابع چگالی احتمال توزیع رایلی به شکل زیر است:

\large f(x; \sigma) = \frac{x}{\sigma^2} e^{-\frac{x^2}{2\sigma^2}}

در این فرمول σ پارامتر مقیاس است که توزیع را مشخص می‌کند. هرچه مقدار  بیشتر باشد، توزیع پهن‌تر و کشیده‌تر می‌شود. x هم متغیر تصادفی است که مقدار آن غیر منفی است.

 ضریب نرمال‌سازی

 ضریبσ2 در مخرج تضمین می‌کند که مساحت زیر منحنی چگالی احتمال برابر با ۱ باشد. درواقع این ضریب توزیع را نرمال می‌کند.

 بخش‌ نمایی

بخش نمایی کاهش تابع چگالی احتمال را با افزایش مقدار x توصیف می‌کند. درواقع، تابع چگالی احتمال با افزایش x به سمت صفر میل می‌کند.

رسم توزیع رایلی با پارامترهای مختلف

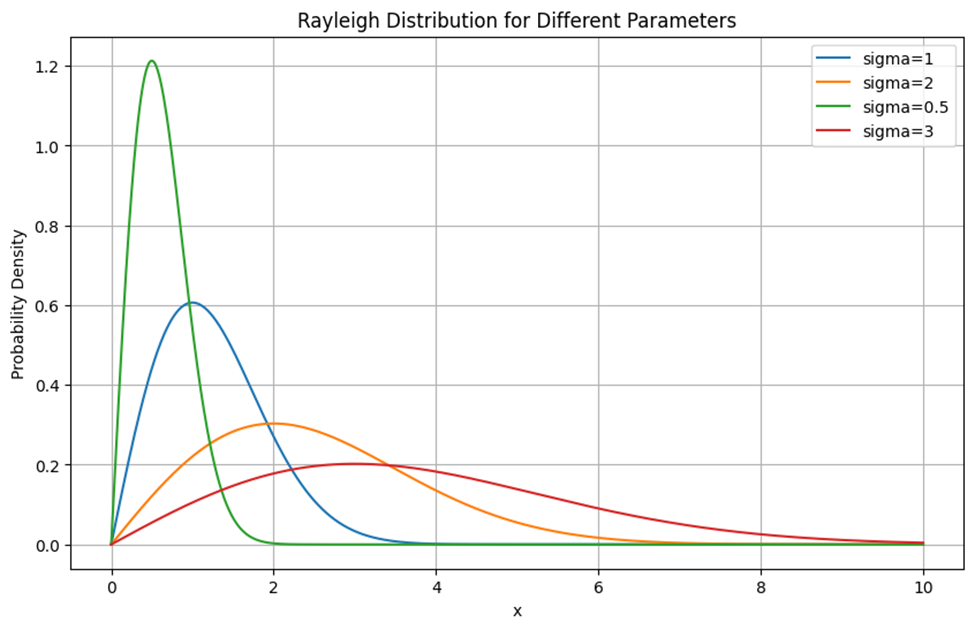
این نمودار تابع چگالی احتمال توزیع رایلی را برای مقادیر مختلف پارامتر σ نشان می‌دهد. با افزایش مقدار σ، پهنای توزیع رایلی بیشتر می‌شود و پیک توزیع به مقادیر بزرگتر x منتقل می‌شود. این امر نشان می‌دهد که با افزایش σ، احتمال وقوع مقادیر بزرگتر x بیشتر می‌شود. مقدار پیک توزیع رایلی با افزایش σ کاهش می‌یابد. این به این دلیل است که برای مقادیر بزرگترِ σ توزیع رایلی پهن‌تر می‌شود و چگالی احتمال در مقادیر بیشتری از x پخش می‌شود.

کاربردهای توزیع رایلی در یادگیری ماشین

پردازش تصویر

در این زمینه، استفاده از توزیع رایلی به بهبود روش‌های حذف نویز و بهبود کیفیت تصویر کمک می‌کند. استفاده از روش‌های آماری و الگوریتم‌های یادگیری ماشین برای شناسایی الگوهای نویزی و جدا کردن آن‌ها از ساختارهای مفید تصویر می‌تواند به بهبود دقت تقسیم‌بندی کمک کند. این روش‌ها می‌توانند از مدل‌های ترکیبی شامل توزیع رایلی برای شناسایی نویز و بافت‌های خاص استفاده کنند.

 شبیه‌سازی و تولید داده‌های مصنوعی

توزیع رایلی برای تولید داده‌های مصنوعی با ویژگی‌های خاص بسیار مفید است. این کاربرد در تست و اعتبارسنجی مدل‌های یادگیری ماشین اهمیت دارد. در بسیاری از موارد، به داده‌های زیادی برای آموزش و ارزیابی مدل‌های یادگیری ماشین نیاز است. اگر داده‌های واقعی به مقدار کافی در دسترس نباشد، می‌توان از توزیع رایلی برای تولید داده‌های مصنوعی با ویژگی‌های مشابه استفاده کرد. این داده‌ها می‌توانند برای بررسی عملکرد الگوریتم‌ها در شرایط مختلف و تست مقاومت مدل‌ها در برابر نویز استفاده شوند.

 تشخیص ناهنجاری‌ها

توزیع رایلی می‌تواند برای تشخیص ناهنجاری‌ها در داده‌ها استفاده شود. برای مثال در سیستم‌های مالی و بانکی، تشخیص تقلب اهمیت زیادی دارد. استفاده از توزیع رایلی برای مدل‌سازی رفتارهای عادی و ناهنجار در داده‌های تراکنش‌ها، به کشف تراکنش‌های مشکوک کمک می‌کند. با تحلیل توزیع داده‌ها و شناسایی انحرافات از الگوی رایلی، می‌توان تقلب‌ها را با دقت بیشتری تشخیص داد. یا در شبکه‌های کامپیوتری که تشخیص ناهنجاری‌ها و حملات سایبری از اهمیت بالایی برخوردار است، استفاده از توزیع رایلی برای تحلیل ترافیک شبکه و شناسایی الگوهای ناهنجار می‌تواند به شناسایی زودهنگام حملات و جلوگیری از آسیب‌های بیشتر کمک کند.

توزیع دریکله

توزیع دیریکله (Dirichlet Distribution) یکی از توزیع‌های احتمالی چندمتغیره است که به طور عمده برای پارامترهای احتمالی استفاده می‌شود. این توزیع، تعمیم توزیع بتا به ابعاد بالاتر است. اگر بخواهیم به زبان ساده بیان کنیم، توزیع دیریکله به ما کمک می‌کند تا احتمال تخصیص دسته‌های مختلف را در یک سیستم چنددسته‌ای مدل‌سازی کنیم.

فرمول ریاضی

تابع چگالی احتمال توزیع دیریکله به صورت زیر تعریف می‌شود:

\large f(x_1, x_2, \ldots, x_k; \alpha_1, \alpha_2, \ldots, \alpha_k) = \frac{\Gamma\left(\sum_{i=1}^k \alpha_i\right)}{\prod_{i=1}^k \Gamma(\alpha_i)} \prod_{i=1}^k x_i^{\alpha_i - 1}

در این فرمول:

• X_iها مقادیر احتمالاتی هستند که باید مجموع آن‌ها برابر یک باشد، یعنی:
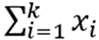
• α_iها پارامتر توزیع و تعیین‌کننده شکل توزیع دریکله هستند. مقادیر بزرگتر  نشان‌دهنده احتمال بیشتر برای Xi مربوطه است.
• Γ تابع گاما است که یک تعمیم از تابع فاکتوریل است و برای محاسبه توزیع‌های پیوسته استفاده می‌شود.

ضریب نرمال‌سازی

بخش مربوط به توابع گاما، تضمین می‌کند که مجموع چگالی‌های احتمال در توزیع دیریکله برابر با یک باشد. به عبارت دیگر، این جزء کاری می‌کند که تابع چگالی احتمال، یک توزیع معتبر باشد.

بخش توانی

این جزء نشان‌دهنده تأثیر پارامترهای توزیع (α_iها) بر مقادیر احتمالاتی x_i است. به عبارت دیگر، هر مقدار احتمالی به توان پارامتر مربوطه منهای یک می‌رسد.

رسم توزیع دریکله برای پارامترهای مختلف

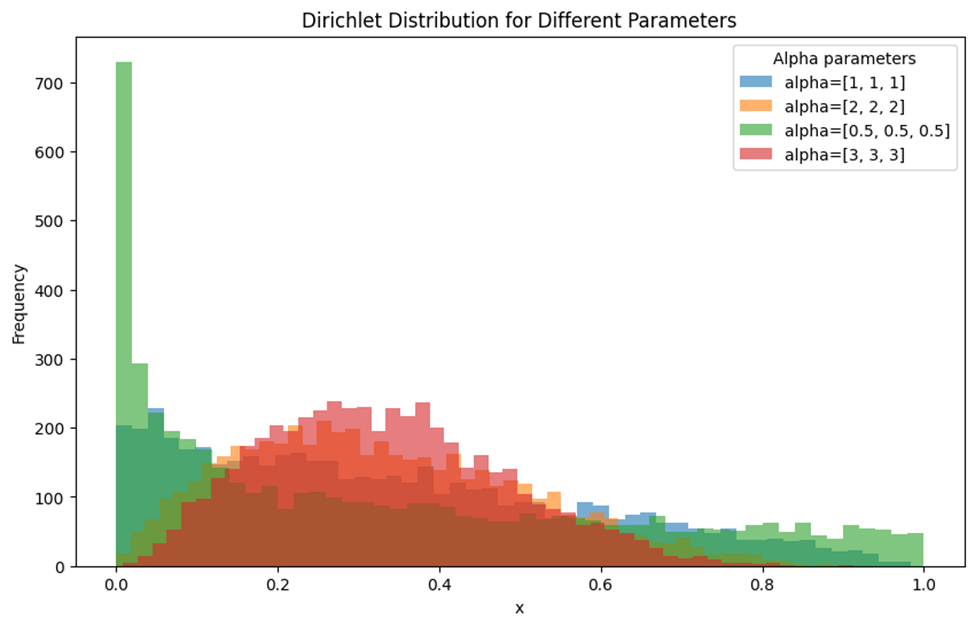
این نمودار توزیع دیریکله را با پارامترهای مختلف آلفا نشان می‌دهد. خطوط رنگی مختلف نمایانگر توزیع دیریکله با پارامترهای مختلف هستند. برای مثال خط آبی (alpha = [1, 1, 1]) توزیع دیریکله تقریباً یکنواخت را نشان می‌دهد. این بدان معنی است که تمامی مقادیر x با احتمال تقریباً یکسان ظاهر می‌شوند. قسمت نارنجی رنگ، توزیع نسبتاً متعادلی است، اما در نقاطی حول میانگین (حدودا نقطه x=0.5) تمرکز و تجمع بیشتری دارد. توزیع سبز (alpha = [0.5, 0.5, 0.5]) نشان می‌دهد که مقادیر نزدیک به صفر بیشترین فراوانی را دارند. این پارامترها منجر به توزیعی می‌شوند که اکثر داده‌ها نزدیک به صفر متمرکز هستند و سپس به سرعت کاهش می‌یابد. توزیع قرمزرنگ نشان می‌دهد که داده‌ها به طور متوازن‌تر توزیع شده‌اند و بیشترین فراوانی در مقادیر حول میانگین قرار دارد.

توزیع دیریکله در یادگیری ماشین

در ادامه کاربردهای این توزیع در یادگیری ماشین را بررسی می‌کنیم:

مدل‌سازی موضوعی

مدل‌سازی موضوعی (Topic Modeling) یک تکنیک مهم در پردازش زبان طبیعی (NLP) و یادگیری ماشین است که برای استخراج موضوعات پنهان در مجموعه‌های بزرگی از اسناد متنی استفاده می‌شود. این تکنیک به کمک الگوریتم‌های مختلف به شناسایی الگوهای مشترک در متون می‌پردازد و از طریق آن‌ها موضوعات یا دسته‌بندی‌های پنهان را کشف می‌کند. در مدل‌سازی موضوعی، هر سند به عنوان ترکیبی از چند موضوع و هر موضوع به عنوان ترکیبی از چند کلمه مدل می‌شود. به عبارت دیگر، فرض می‌شود که هر سند از چند موضوع تشکیل شده و هر موضوع نیز از کلمات مختلفی که با احتمال‌های مختلفی در آن موضوع حضور دارند، تشکیل شده است.

تخصیص پنهان دیریکله (LDA یا Latent Dirichlet Allocation) یکی از معروف‌ترین الگوریتم‌ها برای مدل‌سازی موضوعات در متون است. این الگوریتم از توزیع دیریکله به عنوان یک توزیع پیشین (prior) استفاده می‌کند تا توزیع احتمالی موضوعات در اسناد و همچنین توزیع کلمات در موضوعات را مدل‌سازی کند.

یادگیری ماشین بیزی

در یادگیری ماشین بیزی، توزیع دیریکله به عنوان توزیع پیشینی مشترک برای پارامترهای مدل‌های مختلف استفاده می‌شود. این توزیع به دلیل خواص ریاضیاتی خاص خود، مانند بسته بودن تحت تجمع، محاسبات بیزی را ساده‌تر می‌کند و به روزرسانی‌های پارامتری را به شکل کارآمدتری انجام می‌دهد.

شبیه‌سازی مونت‌ کارلو

همچنین در شبیه‌سازی و شبیه‌سازی مونت‌ کارلو (Monte Carlo) توزیع دیریکله نقش مهمی ایفا می‌کند. این توزیع به عنوان یک توزیع پیشینی قابل انعطاف برای شبیه‌سازی داده‌های چند‌متغیره به کار می‌رود و کمک می‌کند تا نتایج شبیه‌سازی به واقعیت نزدیک‌تر باشند.

تخصیص منابع در سیستم‌های توصیه‌گر

در سیستم‌های توصیه‌گر، هدف اصلی ارائه پیشنهادهای شخصی‌سازی شده به کاربران است. این پیشنهادها بر اساس تحلیل داده‌های تاریخی و رفتارهای گذشته کاربران انجام می‌شود. یکی از روش‌های موثر برای مدل‌سازی ترجیحات کاربران استفاده از مدل‌های بیزی است که در اینجا توزیع دیریکله نقش مهمی ایفا می‌کند. به‌عنوان مثال، در مدل‌های توصیه‌گر بیزی، توزیع دیریکله به عنوان پیشین برای پارامترهای ترجیح کاربران نسبت به آیتم‌های مختلف استفاده می‌شود.

توزیع‌های گسسته

داده‌های گسسته، داده‌هایی هستند که فقط می‌توانند مقادیر مشخص و محدود داشته باشند. به عبارت دیگر، این نوع داده‌ها نمی‌توانند بین دو مقدار پیوسته باشند و همیشه به صورت عددی خاص و معین ظاهر می‌شوند.

 تفاوت بین داده‌های گسسته و پیوسته

داده‌های گسسته و پیوسته دو نوع اصلی داده‌ها هستند که در آمار و تحلیل داده‌ها مورد استفاده قرار می‌گیرند. داده‌های گسسته مقادیر محدود و مشخص دارند، در حالی که داده‌های پیوسته می‌توانند هر مقداری در یک بازه مشخص را بپذیرند. به عنوان مثال، وزن یک فرد یا دمای هوا نمونه‌هایی از داده‌های پیوسته هستند اما تعداد دانش‌آموزان یک کلاس یا تعداد خودروهای موجود در یک پارکینگ از نوع داده‌های گسسته هستند.

انواع توزیع داده‌های گسسته

توزیع داده‌های گسسته انواع مختلفی دارد که هر یک از آن‌ها در شرایط خاصی کاربرد دارند. در ادامه به برخی از این توزیع‌ها اشاره می‌کنیم:

توزیع پواسون

توزیع پواسون برای مدل‌سازی تعداد رخدادها در یک بازه زمانی یا فضایی مشخص که به صورت تصادفی و با نرخ ثابتی رخ می‌دهند، استفاده می‌شود. این توزیع معمولاً برای تحلیل رخدادهای نادر یا غیرمنتظره کاربرد دارد، مانند تعداد تماس‌های دریافتی در یک مرکز تماس در یک ساعت مشخص.

فرمول ریاضی

\large P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}

در این فرمول:

•  احتمال وقوع k رویداد در یک بازه زمانی یا فضایی مشخص است.
• λ میانگین نرخ وقوع رویدادها در بازه زمانی یا فضایی مشخص است.
• e پایه لگاریتم طبیعی (تقریباً برابر با 2.71828) است.
• k تعداد رویدادها است.

توزیع دو جمله‌ای

توزیع دو جمله‌ای یکی از مهم‌ترین و پرکاربردترین توزیع‌های گسسته است. این توزیع برای مدل‌سازی تعداد موفقیت‌ها در یک سری از آزمایشات مستقل با احتمال ثابت موفقیت مورد استفاده قرار می‌گیرد. به عنوان مثال، تعداد پرتاب‌های موفق یک سکه در ده بار پرتاب می‌تواند به صورت توزیع دو جمله‌ای مدل‌سازی شود.

فرمول ریاضی

\large P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}

در این فرمول:

• P(X=k) احتمال وقوع k موفقیت در n آزمایش است.
• p احتمال موفقیت در هر آزمایش است.
• 1−p احتمال شکست در هر آزمایش است.
• n تعداد کل آزمایش‌ها است.
• k تعداد موفقیت‌ها است.

توزیع چندجمله‌ای

توزیع چندجمله‌ای (Multinomial Distribution) یک تعمیم از توزیع دوجمله‌ای است که در آن هر آزمایش می‌تواند بیش از دو نتیجه ممکن داشته باشد. برای مثال، تعداد دفعات وقوع هر یک از چندین نوع مختلف خرچنگ در یک نمونه‌برداری از اقیانوس.

فرمول ریاضی

\large P(X_1 = x_1, X_2 = x_2, \ldots, X_k = x_k) = \frac{n!}{x_1! x_2! \cdots x_k!} p_1^{x_1} p_2^{x_2} \cdots p_k^{x_k}

در این فرمول:

• P(X₁=x₁, X₂=x₂, …, X_k=x_k) احتمال مشاهده x₁ وقوع از نوع یک، x₂ ​وقوع از نوع دو، …، x_k وقوع از نوع k است.
• n تعداد کل آزمایش‌ها است.
• x₁​,x₂​,…,x_k تعداد وقوع‌های هر نوع است.
• p₁​,p₂​,…,p_k​ احتمال وقوع هر نوع است.

توزیع هندسی

توزیع هندسی یکی دیگر از توزیع‌های گسسته است که برای مدل‌سازی تعداد آزمایشات لازم تا اولین موفقیت مورد استفاده قرار می‌گیرد. به عنوان مثال، تعداد بارهایی که یک سکه را پرتاب می‌کنیم تا اولین بار شیر بیاید، می‌تواند به صورت توزیع هندسی مدل‌سازی شود.

فرمول ریاضی

\large P(X = k) = (1 - p)^{k-1} p

در این فرمول:

• P(X=k) احتمال این که اولین موفقیت در kامین آزمایش رخ دهد.
• p احتمال موفقیت در هر آزمایش
• 1−p احتمال شکست در هر آزمایش
• k شماره آزمایشی که در آن اولین موفقیت رخ می‌دهد.

توزیع داده‌های واقعی

داده‌های واقعی اغلب دارای توزیع‌های پیچیده و غیرنرمال هستند که نیاز به تحلیل دقیق دارند. برای مثال، داده‌های جمع‌آوری شده از کاربران یک وب‌سایت ممکن است دارای توزیع پواسون یا نمایی باشند. در تحلیل داده‌های واقعی، شناخت و درک دقیق توزیع داده‌ها از اهمیت ویژه‌ای برخوردار است، چرا که انتخاب صحیح مدل‌های آماری و روش‌های تحلیل به آن وابسته است.

چالش‌های کار با داده‌های واقعی

کار با داده‌های واقعی می‌تواند چالش‌برانگیز باشد زیرا این داده‌ها اغلب دارای نویز و کمبود داده هستند. همچنین، توزیع‌های پیچیده و غیرقابل پیش‌بینی می‌توانند تحلیل داده‌ها را دشوار کنند. این چالش‌ها نیازمند تکنیک‌های پیشرفته پردازش داده مانند پاکسازی داده، نرمال‌سازی و استفاده از الگوریتم‌های یادگیری ماشین برای مدیریت و تحلیل موثر هستند. به عنوان مثال، داده‌های ناپیوسته و دارای مقادیر مفقود می‌توانند مدل‌های پیش‌بینی را دچار خطا کنند و نیاز به تکنیک‌های خاصی مانند جایگزینی مقادیر مفقود با میانگین یا مد، یا استفاده از الگوریتم‌های پیش‌بینی‌کننده برای تخمین این مقادیر دارند.

Skewness در داده‌ها

Skewness یا چولگی یکی از مفاهیم آماری است که نشان‌دهنده عدم تقارن توزیع داده‌ها نسبت به میانگین آن‌ها است. به عبارت دیگر، چولگی مشخص می‌کند که داده‌ها بیشتر به سمت کدام طرف (چپ یا راست) کشیده شده‌اند. چولگی به سه دسته کلی تقسیم می‌شود:

چولگی مثبت (Right-skewed or Positive Skewness)

در این حالت، دنباله توزیع به سمت راست (اعداد بزرگتر) کشیده شده است. بیشتر داده‌ها در سمت چپ میانگین قرار دارند. نمودار هیستوگرام چنین توزیعی به سمت راست کشیده شده است.

چولگی منفی (Left-skewed or Negative Skewness)

در این حالت، دنباله توزیع به سمت چپ (اعداد کوچکتر) کشیده شده است. بیشتر داده‌ها در سمت راست میانگین قرار دارند. نمودار هیستوگرام چنین توزیعی به سمت چپ کشیده شده است.

توزیع نرمال (No Skewness or Symmetrical Distribution)

در این حالت، توزیع داده‌ها نسبت به میانگین متقارن است و هیچ چولگی خاصی مشاهده نمی‌شود. داده‌ها به طور یکنواخت در دو طرف میانگین قرار دارند.

تکنیک‌های مقابله با Skewness

برای رفع مشکل چولگی در داده‌های واقعی، می‌توان از تکنیک‌های مختلفی استفاده کرد. یکی از این تکنیک‌ها، استفاده از تبدیل‌های ریاضی مانند تبدیل لگاریتمی یا تبدیل Box-Cox است. در ادامه، توضیحات بیشتری درباره این روش‌ها برای مقابله با چولگی آورده شده است:

تبدیل لگاریتمی

یکی از روش‌های معمول برای نرمال‌سازی داده‌های دارای چولگی مثبت است. این تبدیل مقادیر بزرگ را کوچک‌تر می‌کند و توزیع را متقارن‌تر می‌کند. معمولاً برای داده‌هایی که فقط مقادیر مثبت دارند استفاده می‌شود.

تبدیل Box-Cox

تبدیل Box-Cox یک تبدیل ریاضی انعطاف‌پذیر است که برای نرمال‌سازی داده‌ها و کاهش چولگی آن‌ها استفاده می‌شود. این تبدیل توسط دو آماردان به نام‌های جورج باکس (George Box) و دیوید کاکس (David Cox) معرفی شده است. تبدیل Box-Cox به طور خودکار بهترین پارامتر تبدیل را پیدا می‌کند که داده‌ها را به توزیع نرمال نزدیک‌تر کند.

تغییر مقیاس داده‌ها

تغییر مقیاس داده‌ها یکی از مراحل حیاتی در پیش‌پردازش داده‌ها برای یادگیری ماشین و تحلیل داده‌ها است. این فرآیند شامل تغییر اندازه داده‌ها به صورتی است که درک و استفاده از آنها برای مدل‌های یادگیری ماشین آسان‌تر شود. این عمل به مدل‌ها کمک می‌کند تا بتوانند بهتر و دقیق‌تر الگوها و روابط موجود در داده‌ها را بیاموزند.

روش‌های تغییر مقیاس داده‌ها

روش‌های مختلفی برای تغییر مقیاس داده‌ها وجود دارد که شامل استانداردسازی (Standardization) و نرمال‌سازی (Normalization) می‌شود.

استانداردسازی

استانداردسازی به معنای تغییر مقیاس داده‌ها به صورتی است که میانگین داده‌ها صفر و انحراف معیار آن‌ها یک باشد. این روش به خصوص زمانی مفید است که داده‌ها دارای توزیع نرمال باشند. فرمول استاداردسازی به‌شکل زیر است:

\large z = \frac{X - \mu}{\sigma}

نرمال‌سازی

نرمال‌سازی به معنای تغییر مقیاس داده‌ها به صورتی است که تمامی مقادیر بین صفر و یک قرار گیرند. این روش به خصوص زمانی مفید است که داده‌ها دارای مقیاس‌های متفاوتی باشند. فرمول نرمال‌ساز یبه‌شکل زیر است:

\large X' = \frac{X - X_{\text{min}}}{X_{\text{max}} - X_{\text{min}}}

مزایای تغییر مقیاس داده‌ها

تغییر مقیاس داده‌ها می‌تواند به بهبود عملکرد مدل‌های یادگیری ماشین کمک کند. این فرآیند می‌تواند باعث شود که داده‌ها به‌طور یکنواخت در بازه‌ای مشخص پخش شوند و مدل‌ها بتوانند بهتر الگوهای موجود در داده‌ها را یاد بگیرند. همچنین، نرمال‌سازی داده‌ها می‌تواند از بروز مسائل مربوط به مقیاس‌های مختلف داده‌ها جلوگیری کند.

اهمیت بصری‌سازی داده‌ها

بصری‌سازی داده‌ها یکی از ابزارهای کلیدی در تحلیل توزیع داده‌های واقعی است. نمودارها و گراف‌ها می‌توانند الگوها و ناهنجاری‌های موجود در داده‌ها را به وضوح نشان دهند و فرآیند تصمیم‌گیری را تسهیل کنند. نمودارهای هیستوگرام، جعبه‌ای و پراکندگی ابزارهای موثری برای نمایش توزیع و تحلیل داده‌ها هستند. از طریق بصری‌سازی، تحلیلگران می‌توانند به سرعت نقاط قوت و ضعف مدل‌های خود را شناسایی کرده و بهبودهای لازم را اعمال کنند.

بررسی و تحلیل توزیع داده واقعی یکی از مهمترین مراحل در فرآیند علم داده و تحلیل آماری است. با درک درست توزیع داده و استفاده از تکنیک‌های مناسب، می‌توان دقت و کارایی مدل‌های تحلیلی را بهبود بخشید و تصمیم‌گیری‌های بهتری انجام داد.

معرفی ابزارهای تحلیل توزیع داده

ابزارهای مختلفی برای تحلیل توزیع داده‌ها وجود دارد که شامل نرم‌افزارهای آماری و کتابخانه‌های پایتون مانند Pandas و NumPy می‌شود. این ابزارها به تحلیل دقیق‌تر و سریع‌تر توزیع داده‌ها کمک می‌کنند. استفاده از این ابزارها به کاربران امکان می‌دهد تا به صورت جامع و دقیق‌تر به بررسی داده‌ها بپردازند و درک بهتری از توزیع داده‌ها و الگوهای موجود در آن‌ها به دست آورند. این نرم‌افزارها و کتابخانه‌ها با ارائه امکانات پیشرفته و کاربردی می‌توانند فرآیند تحلیل داده‌ها را ساده‌تر و موثرتر کنند.

 نرم‌افزارهای آماری

نرم‌افزارهای آماری مانند SPSS ،SAS و R از جمله ابزارهای قدرتمندی هستند که به تحلیل‌گران داده امکان می‌دهند تا توزیع داده را به صورت دقیق و جامع تحلیل کنند. این نرم‌افزارها با ارائه انواع نمودارها، آزمون‌های آماری و روش‌های تحلیلی متنوع می‌توانند به شناسایی توزیع داده و استخراج اطلاعات مفید کمک کنند. استفاده از این نرم‌افزارها به تحلیل‌گران کمک می‌کند تا بتوانند داده‌ها را به صورت بصری مشاهده کنند و الگوها و روابط موجود در آن‌ها را شناسایی کنند.

 کتابخانه‌های پایتون

کتابخانه‌های پایتون مانند Pandas و NumPy ابزارهای قدرتمندی برای تحلیل داده‌ها فراهم می‌کنند.  Pandas با ارائه امکاناتی برای مدیریت و دستکاری داده‌ها، امکان ایجاد DataFrameهای ساختاریافته و انجام عملیات تحلیلی پیچیده را فراهم می‌کند. NumPy نیز با ارائه قابلیت‌های محاسباتی پیشرفته و امکان انجام عملیات ریاضی و آماری پیچیده، به تحلیل دقیق‌تر داده‌ها کمک می‌کند. این کتابخانه‌ها به همراه دیگر کتابخانه‌های پایتون مانند Matplotlib و Seaborn برای ایجاد نمودارهای گرافیکی و مصورسازی داده‌ها استفاده می‌شوند.

برای مطالعه بیشتر کلیک کنید: طرز مصورسازی مناسب داده ها چگونه است و چطور داده‌ها را مصورسازی کنیم؟

 نحوه استفاده از ابزارها

استفاده از این ابزارها می‌تواند به تحلیل دقیق‌تر و سریع‌تر توزیع داده‌ها کمک کند. این ابزارها می‌توانند به کاربر کمک کنند تا الگوهای موجود در داده‌ها را شناسایی کند و توزیع مناسب برای داده‌ها را انتخاب کند. برای استفاده موثر از این ابزارها، مراحل زیر پیشنهاد می‌شود:

بارگذاری داده‌ها

ابتدا داده‌ها را به وسیله کتابخانه Pandas یا نرم‌افزار آماری مورد نظر بارگذاری می‌کنیم:

# بارگذاری مجموعه داده
import pandas as pd
data = pd.read_csv('dataset.csv')
# نمایش پنج سطر اول داده‌ها
data.head()

خروجی این کد برای مجموعه داده تایتانیک به‌صورت زیر درمی‌آید:

تحلیل توزیع داده اولیه

با استفاده از توابع توصیفی مانند describe در Pandas یا توابع آماری مشابه در نرم‌افزارهای آماری، یک تحلیل اولیه از داده‌ها انجام می‌دهیم:

# تحلیل توزیع اولیه داده‌ها
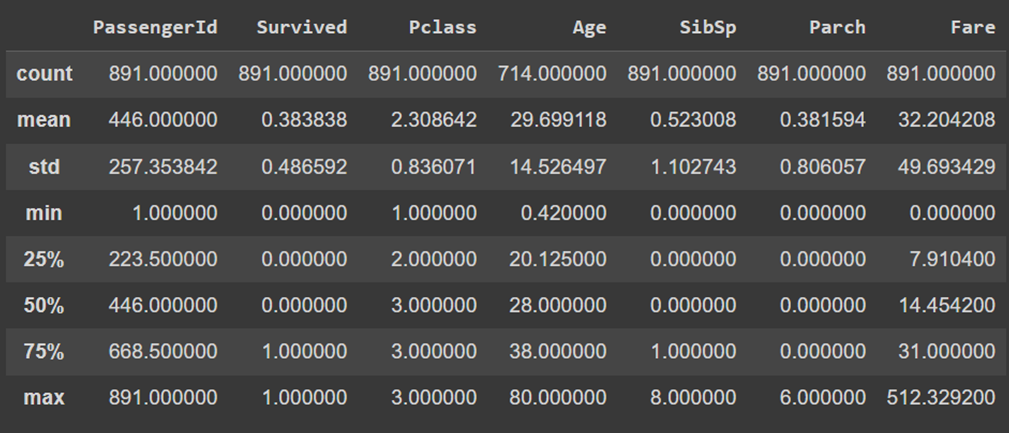
data.describe()

خروجی این کد به‌صورت زیر است:

بصری‌سازی داده‌ها

می‌توانیم با استفاده از نمودارهای هیستوگرام، جعبه‌ای (Box Plot) و پراکندگی (Scatter Plot)، توزیع داده را بصری‌سازی کنیم. کتابخانه‌هایی مانند Matplotlib و Seaborn در پایتون می‌توانند برای این منظور استفاده شوند.

برای رسم هیستوگرام ویژگی‌های (Features) این مجموعه‌داده از کد زیر استفاده می‌کنیم:

import matplotlib.pyplot as plt
import seaborn as sns
# هیستوگرام
data.hist(bins=30, figsize=(10, 8))
plt.show()

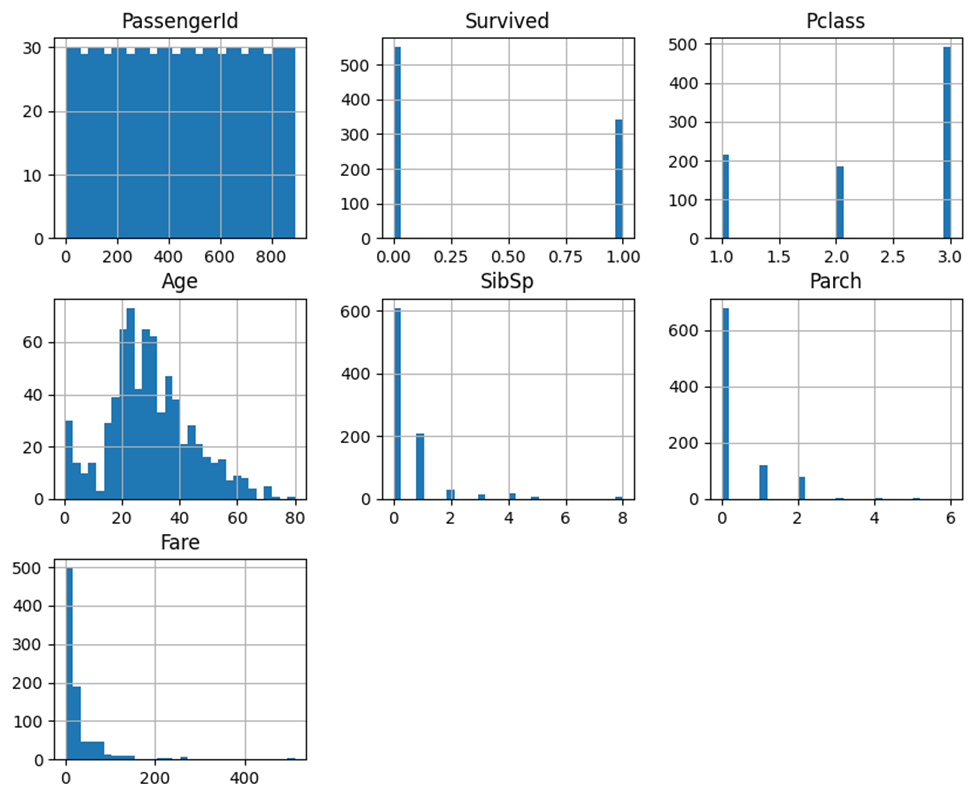
می‌توانیم نمودار جعبه‌ای ویژگی سن را برای پیداکردن داده‌های پرت رسم کنیم:

# نمودار جعبه‌ای برای ویژگی سن
plt.figure(figsize=(10, 8))
sns.boxplot(y=data['Age'])
plt.show()

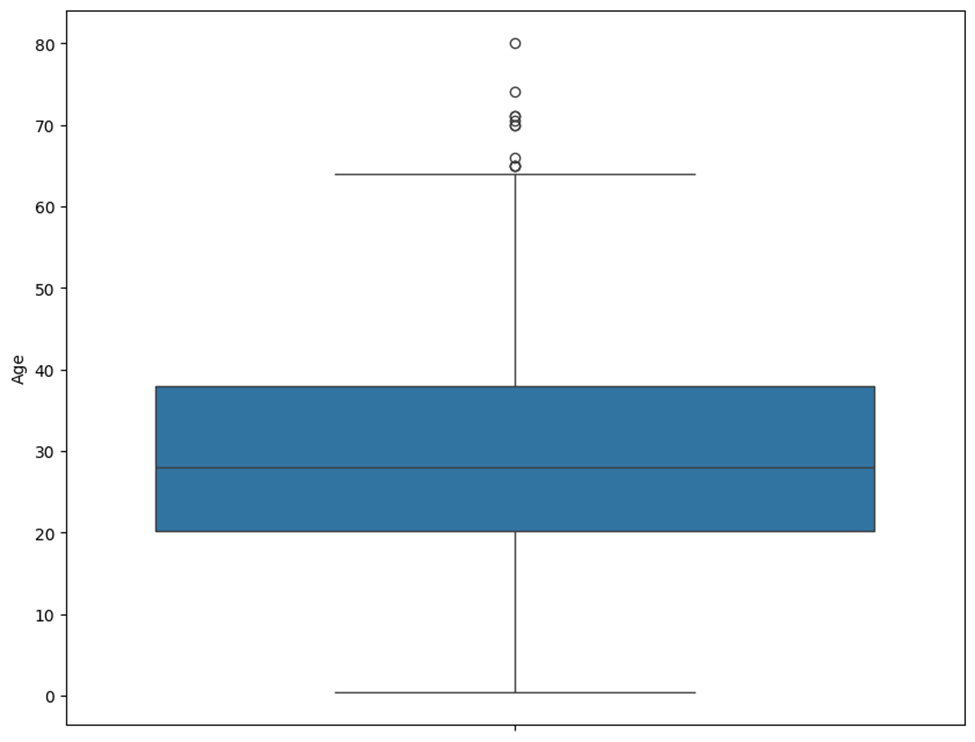
نمودار پراکندگی ویژگی سن در مقابله کرایه بلیت هر مسافر کشتی تایتانیک را نیز با کد زیر رسم می‌کنیم:

# نمودار پراکندگی برای ویژگی سن در مقابل قیمت بلیت
plt.figure(figsize=(10, 8))
sns.scatterplot(x=data['Age'], y=data['Fare'])
plt.show()

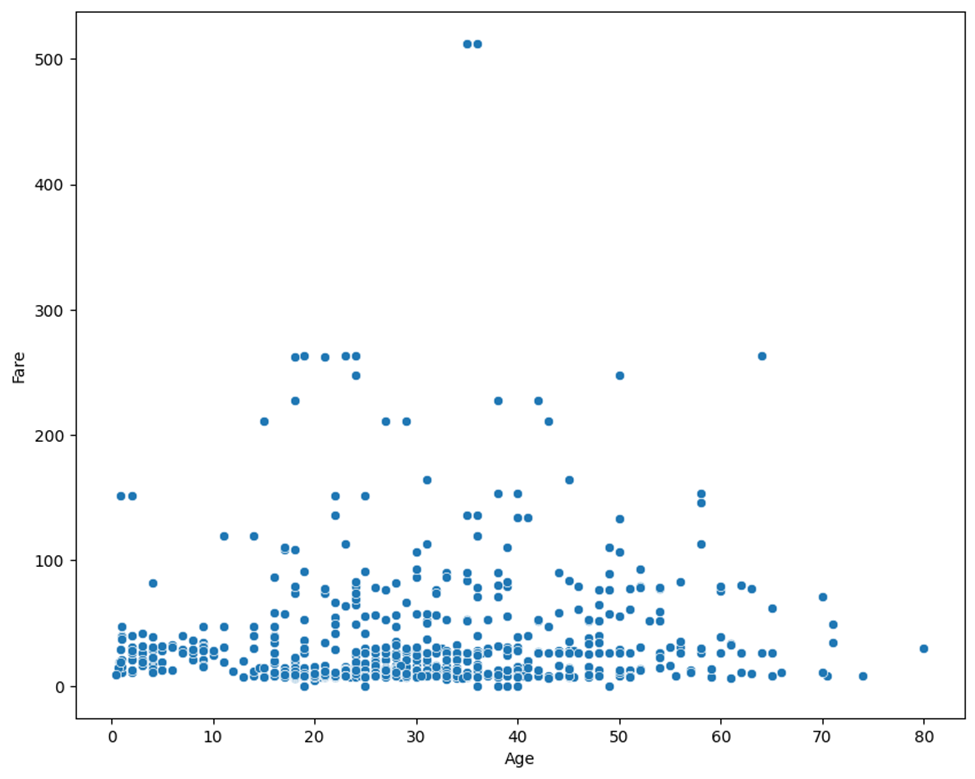
آزمون‌های آماری

 از آزمون‌های آماری مانند آزمون شاپیرو-ویلک (Shapiro-Wilk Test) و آزمون کولموگروف-اسمیرنوف (Kolmogorov-Smirnov Test) برای بررسی نرمال بودن داده‌ها استفاده می‌کنیم. این دو آزمون برای بررسی نرمال بودن توزیع داده‌ها استفاده می‌شوند. نتایج این آزمون‌ها به شکل آماری (Statistics) و مقدار پی (p-value) گزارش می‌شوند.

from scipy.stats import shapiro, kstest

# حذف مقادیر گمشده در ستون سن
age_data = data['Age'].dropna()

# آزمون شاپیرو-ویلک برای بررسی نرمال بودن داده‌ها
stat, p = shapiro(age_data)
print('Shapiro-Wilk Test: Statistics=%.3f, p=%.3f' % (stat, p))

# آزمون کولموگروف-اسمیرنوف برای بررسی نرمال بودن داده‌ها
stat, p = kstest(age_data, 'norm')
print('Kolmogorov-Smirnov Test: Statistics=%.3f, p=%.3f' % (stat, p))

Shapiro-Wilk Test: Statistics=0.981, p=0.000
Kolmogorov-Smirnov Test: Statistics=0.965, p=0.000

در ادامه توضیحی در مورد نتایج چاپ شده در خروجی کد بالا ارائه شده است:

 نتایج آزمون شاپیرو-ویلک:

متغیر Statistics مقدار آماره آزمون شاپیرو-ویلک را دارد. این مقدار به ما نشان می‌دهد که داده‌ها تا چه حد به توزیع نرمال نزدیک هستند. مقداری نزدیک به یک نشان‌دهنده این است که داده‌ها به توزیع نرمال نزدیک‌تر هستند.

مقدار p-value نشان‌دهنده احتمال رد فرضیه صفر (که داده‌ها از توزیع نرمال پیروی می‌کنند) است. مقدار p کمتر از ۰.۰۵ (یا هر سطح معناداری که تعیین شود، مثلاً ۰.۰۱) نشان‌دهنده این است که فرضیه صفر رد می‌شود و داده‌ها از توزیع نرمال پیروی نمی‌کنند.

 نتایج آزمون کولموگروف-اسمیرنوف:

مقدار Statistics آماره آزمون کولموگروف-اسمیرنوف است. این مقدار هم نشان می‌دهد که داده‌ها تا چه حد با توزیع نرمال تطابق دارند. مقدار نزدیک به یک نشان‌دهنده تطابق بیشتر با توزیع نرمال است.

مقدار p-value در این آزمون نیز مشابه آزمون شاپیرو-ویلک است و نشان‌دهنده احتمال رد فرضیه صفر است. مقدار p کمتر از ۰.۰۵ نشان می‌دهد که داده‌ها از توزیع نرمال پیروی نمی‌کنند.

تفسیر نتایج آزمون‌ها

اگرچه آماره هر دو آزمون شاپیرو-ویلک و کولموگروف-اسمیرنوف نزدیک به یک است، اما مقدار p-value صفر نشان می‌دهد که این تطابق به اندازه کافی قوی نیست که فرضیه صفر (نرمال بودن توزیع) را بپذیریم. به عبارت دیگر، تفاوت‌های کوچک بین توزیع داده‌ها و توزیع نرمال در سطح معناداری آزمون دیده می‌شود و به همین دلیل فرضیه صفر رد می‌شود. به‌عبارت دیگر:

• Statistics نزدیک به 1 به ما می‌گوید که تطابق نسبی وجود دارد.
• p-value بسیار کوچک نشان می‌دهد که این تطابق به اندازه‌ای نیست که نرمال بودن توزیع را بپذیریم.

بنابراین، ما می‌توانیم نتیجه بگیریم که داده‌ها از نظر ویژگی سن مسافران چندان نرمال نیستند و ممکن است نیاز به استفاده از تکنیک‌های دیگری برای تحلیل داده‌ها باشد یا داده‌ها را به شکل دیگری نرمال‌سازی کنیم.

محاسبه میزان چولگی و روش‌های رفع آن

در پایتون، برای محاسبه چولگی می‌توان از کتابخانه SciPy استفاده کرد. در ادامه، مثالی از نحوه محاسبه چولگی و ترسیم توزیع آن را برای ویژگی سن مجموعه‌داده تایتانیک داده ارائه می‌شود:

from scipy.stats import skew

# حذف مقادیر گمشده در ستون سن
age_data = data['Age'].dropna()

# محاسبه چولگی
age_skewness = skew(age_data)

# بصری‌سازی توزیع سنی با استفاده از هیستوگرام
plt.figure(figsize=(10, 6))
sns.histplot(age_data, kde=True)
plt.title(f'Distribution of Age with {round(age_skewness, 3)} Skewness')
plt.xlabel('Age')
plt.ylabel('Frequency')
plt.show()

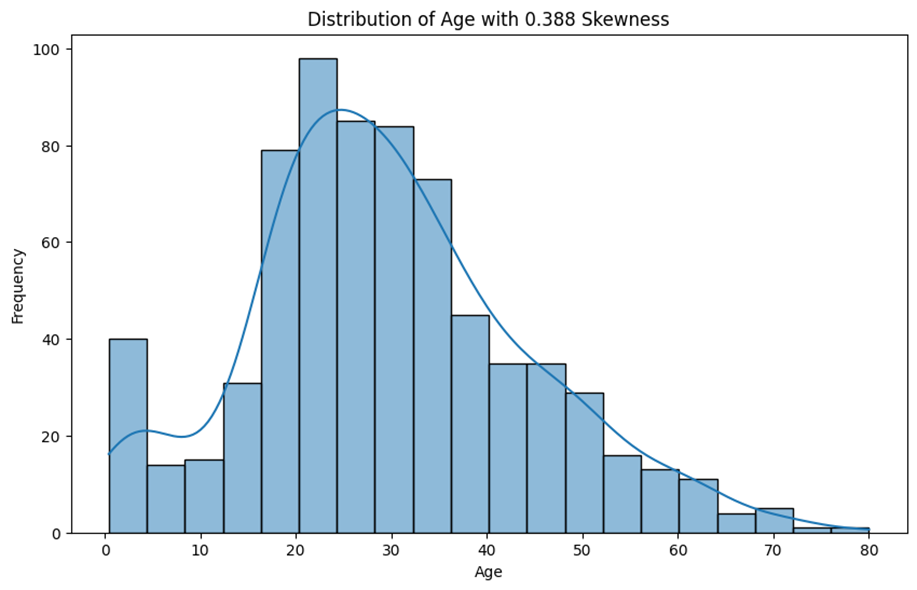
همان‌طور که گفتیم می‌توان برای رفع چولگی از تبدیل‌ لگاریتمی استفاده کرد. البته از آنجایی که لگاریتم ۰ برابر بی‌نهایت خواهد بود، بهتر است از لگاریتم معمولی استفاده نشود و مثلا از log1p که پیش از لگاریتم‌گیری به همه داده‌ها یک مقدار ثابت اضافه می‌کند (تا اگر مقدار ۰ در داده‌ها وجود داشت آن لگاریتم به بی‌نهایت میل نکند) استفاده کرد:

from scipy.stats import boxcox
import numpy as np

# تبدیل لگاریتمی
age_log_transformed = np.log1p(age_data)

# محاسبه چولگی پس از لگاریتم‌گیری
age_skewness = skew(age_log_transformed)

# بصری‌سازی توزیع سنی پس از تبدیل لگاریتمی
plt.figure(figsize=(10, 6))
sns.histplot(age_log_transformed, kde=True)
plt.title(f'Log-Transformed Distribution of Age with {round(age_skewness, 3)} Skewness')
plt.xlabel('Log(Age)')
plt.ylabel('Frequency')
plt.show()

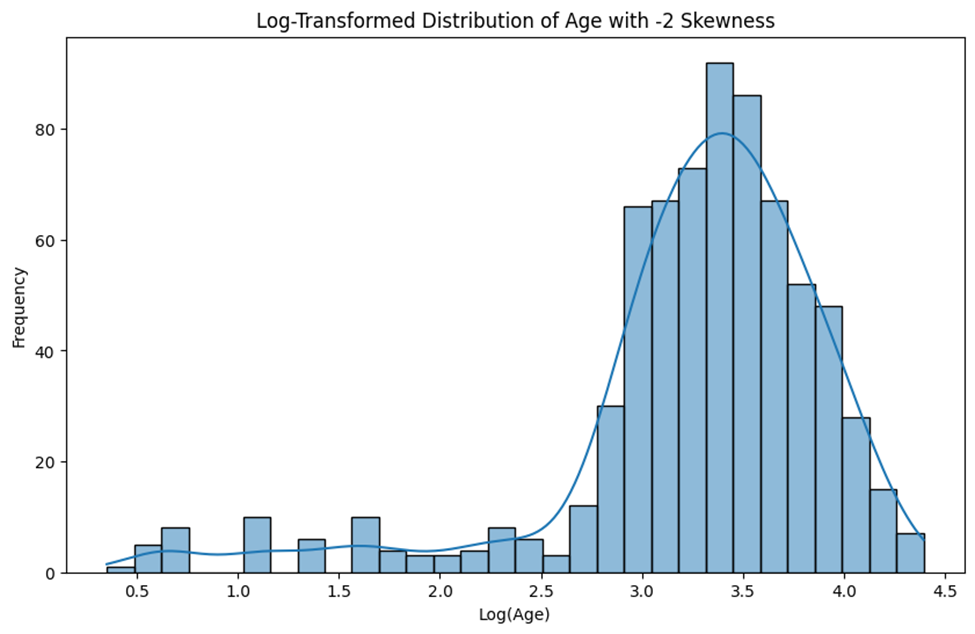
همان‌طور که در نمودار پیداست، این تکنیک برای رفع مشکل چولگی داده ما چندان کارساز نبوده است. زیرا تبدیل لگاریتمی بیشتر برای داده‌هایی که دارای چولگی مثبت بسیار بالا هستند مناسب است در حالی که داده ما تنها ۰.۳۸ چولگی داشت. در این شرایط تکنیم Box-Cox می‌تواند کارآمدتر باشد:

# تبدیل Box-Cox
age_boxcox_transformed, _ = boxcox(age_data)

# محاسبه چولگی بعد از Box-Cox
age_skewness = skew(age_boxcox_transformed)

# بصری‌سازی توزیع سنی پس از تبدیل Box-Cox
plt.figure(figsize=(10, 6))
sns.histplot(age_boxcox_transformed, kde=True)
plt.title(f'Box-Cox Transformed Distribution of Age with {round(age_skewness, 3)} Skewness')
plt.xlabel('Box-Cox(Age)')
plt.ylabel('Frequency')
plt.show()

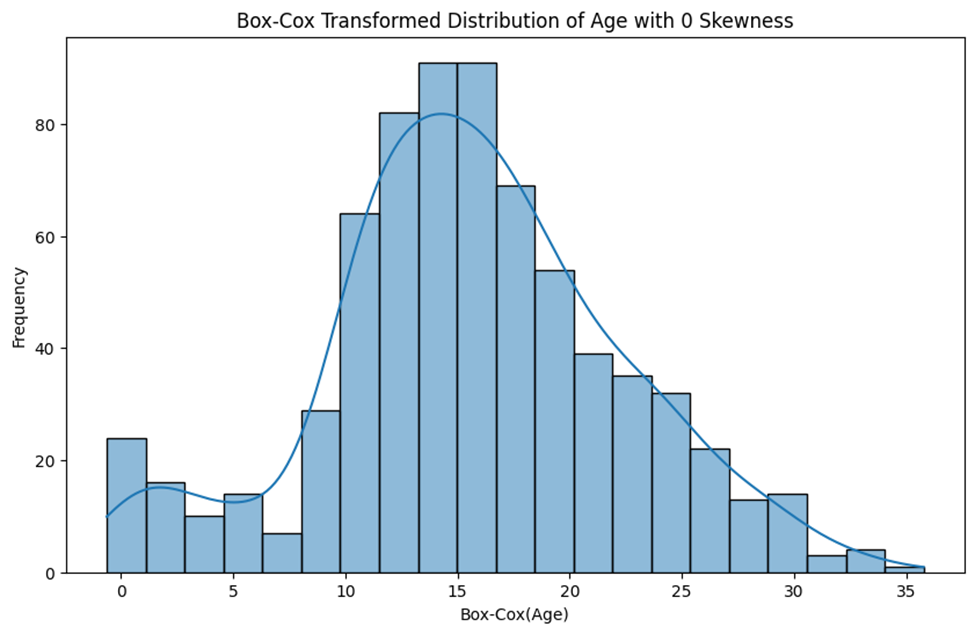
همان‌طور که می‌بینید با این روش، چولگی ویژگی سن کاملا رفع شده است.

تغییر مقیاس داده‌ها

بعد از رفع چولگی، در صورت نیاز به نرمال‌سازی یا استانداردسازی داده‌ها، از توابع مناسب در Pandas یا کتابخانه‌هایی مانند Scikit-Learn استفاده می‌کنیم:

from sklearn.preprocessing import StandardScaler, MinMaxScaler

# تغییر شکل داده‌ها
age_boxcox_transformed = age_boxcox_transformed.reshape(-1, 1)

# استانداردسازی داده‌ها
scaler = StandardScaler()
age_scaled = scaler.fit_transform(age_boxcox_transformed)

# نرمال‌سازی داده‌ها
scaler = MinMaxScaler()
age_normalized = scaler.fit_transform(age_boxcox_transformed)

برای مشاهده توزیع داده‌ها بعد از تغییر مقیاس از کد زیر استفاده می‌کنیم:

plt.figure(figsize=(14, 6))
plt.subplot(1, 2, 1)
sns.histplot(age_scaled, kde=True, legend=False)
plt.title('Standard Age Distribution')
plt.xlabel('Standard Age')
plt.subplot(1, 2, 2)
sns.histplot(age_normalized, kde=True, legend=False)
plt.title('Normalized Age Distribution')
plt.xlabel('Normalized Age')
plt.tight_layout()
plt.show()

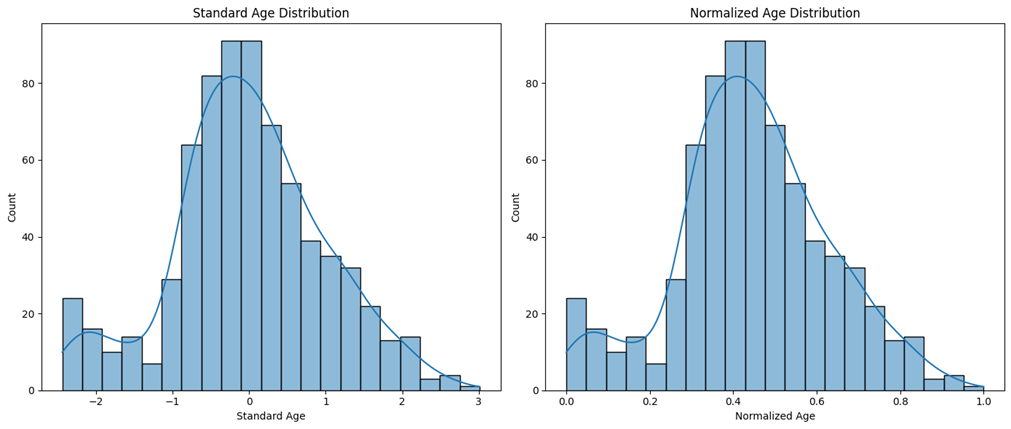
همان‌طور که در شکل مشخص است در حالت استاندارد، میانگین توزیع سنی ۰ و انحراف معیار آن ۱ شده است. در حالت نرمال نیز داده‌ها بین ۰ و ۱ توزیع شده‌اند.

تحلیل نهایی و تفسیر

در پایان نتایج تحلیل‌ها و آزمون‌ها را تفسیر کرده و توزیع مناسب برای داده‌ها را انتخاب می‌کنیم.

این مراحل به تحلیل‌گران کمک می‌کند تا با دقت بیشتری توزیع داده‌ها را بررسی کرده و مدل‌های یادگیری ماشین را با داده‌های بهینه‌سازی‌شده و نرمال‌شده آموزش دهند. استفاده از ابزارهای مناسب می‌تواند به بهبود کیفیت و دقت مدل‌ها کمک کند و از بروز مشکلات ناشی از توزیع نادرست داده‌ها جلوگیری کند.

مجموعه کامل کدهای استفاده شده در این مطلب، از گیت‌هاب ریپوزیتوری Data Distribution قابل دسترسی است.

مطالعات موردی

پیش‌بینی فروش با استفاده از توزیع داده نرمال

از توزیع داده نرمال می‌توان برای پیش‌بینی فروش یک فروشگاه استفاده کرد. توزیع نرمال یا توزیع گاوسی یکی از مهم‌ترین و پرکاربردترین توزیع‌های احتمالی در آمار و یادگیری ماشین است. این توزیع داده شکل زنگوله‌ای دارد و بیشتر داده‌ها در نزدیکی میانگین قرار می‌گیرند. مراحل انجام این کار را در ادامه بررسی می‌کنیم:

• جمع‌آوری داده‌ها: ابتدا داده‌های تاریخی فروش جمع‌آوری می‌شوند. این داده‌ها شامل مقادیر فروش در بازه‌های زمانی مختلف (مثلاً روزانه، هفتگی یا ماهانه) است.
• تحلیل داده‌ها: داده‌های جمع‌آوری شده مورد تحلیل قرار می‌گیرند تا ویژگی‌های آماری نظیر میانگین و انحراف معیار مشخص شوند.
• تعیین پارامترهای توزیع نرمال: توزیع نرمال با استفاده از دو پارامتر تعریف می‌شود: میانگین یا  و انحراف معیار یا . میانگین نشان‌دهنده مرکز توزیع و انحراف معیار نشان‌دهنده میزان پراکندگی داده‌ها اطراف میانگین است.
• ایجاد مدل توزیع نرمال: با استفاده از میانگین و انحراف معیار محاسبه شده، یک مدل توزیع نرمال ساخته می‌شود. این مدل می‌تواند به صورت یک تابع ریاضی  توصیف شود، که N نشان‌دهنده توزیع نرمال، μ میانگین و σ² واریانس (مربع انحراف معیار) است.
• پیش‌بینی با استفاده از مدل: مدل توزیع نرمال ایجاد شده برای پیش‌بینی مقادیر آینده مورد استفاده قرار می‌گیرد. به عنوان مثال، می‌توان با استفاده از این مدل احتمال وقوع مقادیر مختلف فروش را در بازه‌های زمانی مختلف محاسبه کرد.

نمونه عملی

برای مثال فرض کنید داده‌های فروش یک فروشگاه در طول یک سال گذشته جمع‌آوری شده است. میانگین فروش روزانه ۱۰۰ واحد و انحراف معیار ۱۵ واحد است. با استفاده از این اطلاعات، می‌توان یک مدل توزیع نرمال با میانگین ۱۰۰ و انحراف معیار ۱۵ ایجاد کرد. این مدل به ما کمک می‌کند تا بتوانیم پیش‌بینی کنیم که احتمال فروش روزانه در محدوده‌های مختلف (مثلاً بین ۹۰ تا ۱۱۰ واحد) چقدر است.

تحلیل رفتار کاربران با استفاده از توزیع پواسون

در این مطالعه موردی، از توزیع پواسون برای تحلیل رفتار کاربران یک وب‌سایت استفاده می‌شود. این توزیع می‌تواند به تحلیل تعداد بازدیدهای کاربران در یک زمان مشخص و پیش‌بینی تعداد بازدیدهای آینده کمک کند. مراحل انجام این کار را درادامه بررسی می‌کنیم:

• جمع‌آوری داده‌ها: داده‌های مربوط به بازدیدهای کاربران از وب‌سایت در بازه‌های زمانی مختلف (مثلاً ساعتی یا روزانه) جمع‌آوری می‌شوند.
• تحلیل داده‌ها: داده‌های جمع‌آوری شده برای مشخص کردن نرخ وقوع وقایع (مثلاً میانگین تعداد بازدیدها در هر ساعت) تحلیل می‌شوند.
• تعیین پارامترهای توزیع پواسون: توزیع پواسون تنها یک پارامتر دارد که نرخ وقوع رویدادها (λ) است. این پارامتر میانگین تعداد وقوع رویدادها در بازه زمانی یا فضایی مشخص را نشان می‌دهد.
• ایجاد مدل توزیع پواسون: با استفاده از نرخ وقوع (λ) محاسبه شده، مدل توزیع پواسون ساخته می‌شود. این مدل می‌تواند به‌صورت یک تابع ریاضی  تعریف می‌شود، که در آن  احتمال وقوع x رویداد در بازه زمانی یا فضایی مشخص، λ نرخ وقوع و x تعداد رویدادها است.
• پیش‌بینی و تحلیل با استفاده از مدل: مدل توزیع پواسون ایجاد شده برای پیش‌بینی تعداد وقوع رویدادها در آینده و تحلیل رفتار داده‌ها مورد استفاده قرار می‌گیرد. به عنوان مثال، می‌توان با استفاده از این مدل احتمال وقوع تعداد مشخصی از بازدیدهای کاربران در یک روز آینده را محاسبه کرد.

نمونه عملی

فرض کنید داده‌های مربوط به بازدیدهای کاربران از یک وب‌سایت در طول یک ماه جمع‌آوری شده است و میانگین تعداد بازدیدهای روزانه ۵۰ بازدید است. با استفاده از این اطلاعات، می‌توان یک مدل توزیع پواسون با نرخ وقوع ۵۰ بازدید در روز (λ=50) ایجاد کرد. این مدل به ما کمک می‌کند تا بتوانیم پیش‌بینی کنیم که احتمال وقوع تعداد مشخصی بازدید در یک روز آینده چقدر است.

جمع‌بندی

در این مقاله، نقش حیاتی توزیع داده در یادگیری ماشین و تاثیر آن‌ها بر عملکرد مدل‌ها بررسی شد. توزیع داده می‌تواند به طور مستقیم بر دقت و کارایی مدل‌های یادگیری ماشین تاثیر بگذارد و درک درست از این توزیع‌ها برای تحلیل داده‌ها و بهینه‌سازی مدل‌ها ضروری است. توزیع‌های مختلفی مانند توزیع داده نرمال، یکنواخت، نمایی و گاما و کاربردهای آن‌ها در مسائل مختلف یادگیری ماشین مورد بحث قرار گرفت. همچنین، به روش‌های بهینه برای مدیریت و تحلیل توزیع داده اشاره شد که می‌تواند به بهبود دقت و عملکرد مدل‌ها کمک کند.

استفاده از تکنولوژی‌های نوین و هوش مصنوعی می‌تواند فرآیند تحلیل توزیع داده را تسریع و بهبود بخشد و در نهایت منجر به مدل‌های دقیق‌تر و کارآمدتر در کاربردهای عملی شود. با توجه به اهمیت توزیع داده، تحلیل‌گران داده و مهندسان یادگیری ماشین باید به درک عمیق‌تری از این موضوع برسند تا بتوانند مدل‌های بهتری ایجاد کنند و نتایج دقیقی ارائه دهند.

سوالات متداول

چگونه توزیع داده بر عملکرد مدل‌های یادگیری ماشین تاثیر می‌گذارد؟

توزیع داده (Data Distribution) نقش مهمی در عملکرد مدل‌های یادگیری ماشین دارد. اگر توزیع داده به درستی شناسایی نشود، مدل ممکن است دچار بیش‌برازش (Overfitting) یا کم‌برازش (Underfitting) شود. همچنین، مدل‌ها باید با داده‌هایی آموزش ببینند که نماینده‌ای از داده‌های واقعی باشند تا عملکرد بهینه‌ای داشته باشند. به عنوان مثال، در رگرسیون خطی (Linear Regression)، فرض می‌شود که خطاها دارای توزیع نرمال (Normal Distribution) هستند که به پیش‌بینی‌های دقیق‌تر کمک می‌کند.

توزیع داده نرمال در یادگیری ماشین چه کاربردهایی دارد و چرا مهم است؟

توزیع داده نرمال یکی از پرکاربردترین توزیع‌ها در یادگیری ماشین است. این توزیع به دلیل تقارن و خصوصیات آماری خاص خود، در الگوریتم‌های مختلفی مانند رگرسیون خطی، تحلیل مؤلفه‌های اصلی (PCA)، و شبکه‌های عصبی (Neural Networks) به کار می‌رود. به عنوان مثال، در رگرسیون خطی فرض می‌شود که خطاها نرمال توزیع شده‌اند که به بهبود دقت مدل کمک می‌کند.

تفاوت بین توزیع‌های پیوسته و گسسته چیست و چگونه در یادگیری ماشین استفاده می‌شوند؟

توزیع‌های پیوسته (Continuous Distributions) مانند توزیع نرمال و توزیع یکنواخت، داده‌هایی را مدل‌سازی می‌کنند که می‌توانند هر مقدار واقعی را در یک بازه مشخص بپذیرند. در مقابل، توزیع‌های گسسته (Discrete Distributions) مانند توزیع دو جمله‌ای (Binomial Distribution) و توزیع پواسون (Poisson Distribution)، داده‌هایی را مدل‌سازی می‌کنند که فقط مقادیر خاصی را می‌پذیرند. در یادگیری ماشین، توزیع‌های پیوسته برای داده‌های پیوسته مانند وزن و قد و توزیع‌های گسسته برای داده‌های شمارشی مانند تعداد رخدادها استفاده می‌شوند.

چگونه می‌توان توزیع نمایی را در مدل‌سازی زمان‌های بین رخدادها استفاده کرد؟

توزیع نمایی (Exponential Distribution) برای مدل‌سازی زمان‌های بین رخدادها در یک فرآیند پواسون استفاده می‌شود. این توزیع برای مدل‌سازی زمان انتظار تا وقوع یک رویداد بعدی، مانند زمان بین خرابی‌های یک سیستم، بسیار مفید است. در یادگیری ماشین، توزیع نمایی می‌تواند در مدل‌های یادگیری تقویتی (Reinforcement Learning) برای مدل‌سازی زمان‌های بین اقدامات و دریافت پاداش‌ها استفاده شود.

چگونه می‌توان از توزیع‌های گسسته مانند توزیع پواسون و توزیع دو جمله‌ای در مدل‌سازی رخدادهای نادر استفاده کرد؟

توزیع‌های گسسته (Discrete Distributions) مانند توزیع پواسون (Poisson Distribution) و توزیع دو جمله‌ای (Binomial Distribution) برای مدل‌سازی رخدادهای نادر بسیار مفید هستند. توزیع پواسون برای مدل‌سازی تعداد رخدادها در یک بازه زمانی یا فضایی مشخص که به صورت تصادفی و با نرخ ثابت رخ می‌دهند، استفاده می‌شود. این توزیع در تحلیل رخدادهای نادر مانند تعداد تماس‌های دریافتی در یک مرکز تماس یا تعداد خرابی‌های یک سیستم کاربرد دارد. از سوی دیگر، توزیع دو جمله‌ای برای مدل‌سازی تعداد موفقیت‌ها در یک تعداد معین از آزمایش‌های مستقل که هر کدام دو نتیجه ممکن دارند (مانند موفقیت یا شکست) به کار می‌رود. این توزیع در مسائلی مانند تحلیل نرخ خطا در سیستم‌های تشخیص و مدل‌سازی احتمال وقوع یک رویداد خاص کاربرد دارد.

یادگیری تحلیل داده را از امروز شروع کنید!

دنیای داده‌ها جذاب است و دانستن علم داده، توانایی تحلیل داده‌، یا بازاریابی مبتنی بر داده، شما را برای فرصت‌های شغلی بسیاری مناسب می‌کند. فارغ از رشته‌ و پیش‌زمینه‌، می‌توانید حالا شروع کنید و از سطح مقدماتی تا پیشرفته بیاموزید. اگر دوست دارید به این حوزه وارد شوید، پیشنهاد می‌کنیم با کلیک روی این لینک قدم اول را همین حالا بردارید.

مشاوران کافه‌تدریس به شما کمک می‌کنند مسیر یادگیری برای ورود به این حوزه را شروع کنید:

دوره جامع دیتا ساینس و ماشین لرنینگ