موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد. ضریب این درس در کنکور رشته مدیریت کسب و کار ۲ است و اهمیت آن بر داوطلبان پوشیده نیست. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید.
اهمیت درس ریاضی عمومی ۱ و ۲
ریاضی عمومی ۱ و ۲ از دروس پایهای رشتههای مختلف است. اهمیت این درس به سه دلیل عمده بازمیگردد؛ اولین دلیل این است که این درس جزو سرفصلهای امتحانی بسیار مهم رشتههای مختلف است. دلیل دوم به محتوای ارائهشده در این درس بازمیگردد. محتوای این درس بهقدری مهم است که آشنایی با مفاهیم آن به درک مفاهیم سایر درسهای دورهی کارشناسی و سایر مواد آزمون کارشناسیارشد کمک شایانی میکند. سومین دلیل اهمیت این درس و کلاس آنلاین ریاضی عمومی ۱ و ۲ نوع نگاهی است که در حل مسائل این درس وجود دارد؛ این نگاه عاملی اساسی در شکلگیری تفکر انتقادی در حل مسائل است.
در این سری از مقالات برخی از موضوعات مهم دروس را با نگاه آموزشی و به صورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید.
معرفی کلاس آنلاین ریاضی عمومی ۱ و ۲
دامنه و برد
تابع مجموعهای از ورودیها را گرفته و و اعمالی روی آنها انجام میدهد تا در نهایت مجموعهای از خروجیها را تولید کند. پس هر تابع از دو مجموعه ورودی و خروجی تشکیل شده است که به این دو مجموعه دامنه و برد تابع گویند.
دامنه
ما برای گرفتن خروجی از تابع باید مقادیری را به عنوان ورودی به آن بدهیم. این مجموعه ورودی ممکن است محدودیتهایی داشته باشد و تابع به ازای هر عددی در ورودی خروجی درستی به ما ندهد. به مقادیری که میتوانیم به عنوان ورودی به تابع دهیم، دامنه تابع گفته میشود که ممکن است همه اعداد یا مقادیر محدودی را در بر بگیرد.
علاوهبر محدویتهای تابع ما خودمان نیز میتوانیم محدودیتهایی برای تابع مشخص کنیم. برای مثال تابع 2+f=x را در نظر بگیرید. دامنه این تابع تمام اعداد حقیقی است و به عبارتی هر عددی را میتوانیم به عنوان ورودی به این تابع داده و خروجی را از آن دریافت کنیم. اما میتوانیم به دامنه محدودیت دهیم و تنها مجموعه اعداد طبیعی را به عنوان ورودی برای این تابع تعریف کنیم. در ریاضیات دامنه را با D نمایش میدهند.
برد
در ریاضیات، برد یک تابع (برابر با مجموعه تمام خروجیهای تابع است. اگر تابع را به عنوان مجموعهای از زوجهای مرتب در نظر بگیریم، آنگاه مجموعهٔ تمام مؤلفههای دوم آن را برد تابع میگویند. مانند تابع برد توابع نیزمیتواند دارای محدودیتهایی باشد که این محدودیتها به جنس تابع بستگی دارد.
محدودیتهای دامنه
توابع مختلف دامنههای متفاوت دارند. به طور کلی اکثر توابع دامنه آنها اعداد حقیقی است. در ادامه محدودیت دامنه توابع مختلف را بررسی میکنیم:
تابع چند جملهای
این توابع به صورت
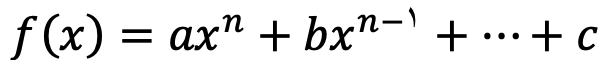
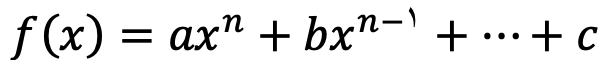
است. این توابع محدودیتی ندارد و دامنه آنها به صورت R است.
تابع کسری
اگر مخرج توابع کسری صفر شود، تابع تعریف نشده خواهد شد. به همین دلیل محدودیت این توابع روی مخرج آن است. دامنه توابع کسری، اعداد حقیقی به جز مقادیری است ریشه مخرج بوده است.
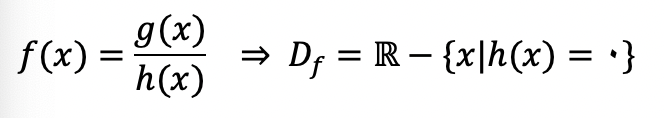
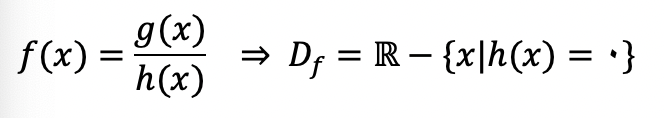
تابع رادیکال
توابع رادیکال به فرجه آنها بستگی دارد. توابع با فرجه فرد به تنهایی محدودیتی ندارند بلکه محدودیت آنها به تابع تحت رادیکال بستگی دارد. در توابع با فرجه زوج اما تابع تحت رادیکال نباید منفی شود به همین دلیل علاوه بر محدودیت تابع تحت رادیکال، باید به این موضوع توجه کنید که تابع تحت رادیکال باید بزرگتر از صفر شود.


تابع لگاریتمی
در توابع لگاریتمی سه محدودیت در دامنه داریم. دو محدودیت روی مبنا و یک محدودیت روی تابع جلوی لگاریتم خواهیم داشت.
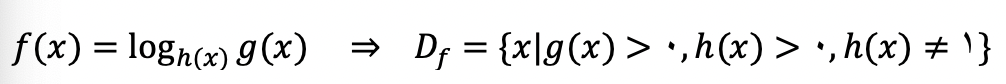
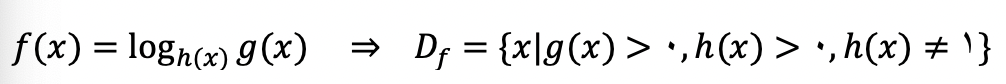
تابع قدرمطلق، جز صحیح، sin، cos
دامنه این توابع اعداد صجیج است و محدودیتی وجود ندارد مگر اینکه تابع تحت توابع دارای محدودیت باشد.
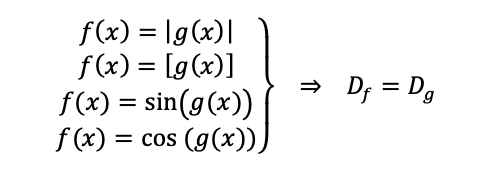
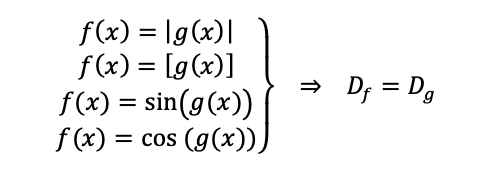
محاسبه برد تابع
روشهای زیادی برای بهدست آوردن برد وجود دارد ولی در کل قانون خاصی به شکل چهارچوب نمیتوان ایجاد کرد.
رسم نمودار
بهترین و ابتداییترین روش تعیین برد یک تابع رسم نمودار تابع بوده، که البته در صورتی از این روش استفاده میکنیم که شکل نمودار تابع را بشناسیم.
دامنه تابع معکوس
از آنجا که با معکوس کردن یک تابع جای دامنه و برد آن عوض میشود، میتوان بای محاسبه برد تابع اصلی، دامنه تابع معکوس را بهدست آورد به طوری که ابتدا تابع معکوس نموده و سپس با قوانین دامنه، دامنه آن را تعیین میکنیم.
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:


سلام ، خسته نباشید. ممنونم از توضیحات خوب شما
امیدواریم مفید بوده باشه