با رویه ها در ریاضی عمومی چقدر آشنا هستید؟ در هندسه تحلیلی رویه‌های درجه دوم در فضای سه‌بعدی دسته‌ای از رویه‌ها هستند که به‌این صورت تعریف می‌شوند: مکان هندسی همه نقاطی مانند  P(x,y,z) که در معادله F(x,y,z)=0 صدق کنند که F یک تابع درجه دو است؛ برای مثال، کُره یک رویه درجه‌دو است؛ زیرا معادله استاندارد کره یک معادله درجه‌دو است. در اینجا رویه های درجه ۲ را که در فضای سه‌بعدی قرار دارند بررسی می‌کنیم.

فهرست مطالب پنهان‌کردن فهرست
  1. 1. انواع رویه ها در ریاضی عمومی
  2. 2. سطوح حاصل از دوران
  3. 3. استوانه
  4. 4. رویه‌های درجه دوم
    1. 4.1. بیضی‌گون
    2. 4.2. هذلولی‌گون
    3. 4.3. سهمی‌گون
  5. 5. مخروط
  6. 6. کلاس آنلاین ریاضی عمومی ۱ و ۲

انواع رویه ها در ریاضی عمومی

در ریاضیات رویه‌ها به ۳ دسته تقسیم می‌شوند:

  1. سطوح حاصل از دوران
  2. استوانه
  3. رویه های درجه دوم

در ادامه هر یک از این رویه ها در ریاضی عمومی را توضیح خواهیم داد.

سطوح حاصل از دوران

هر گاه یک سطح دوبعدی را حول یکی از محورهای مختصات دوران دهیم، رویه حاصل از دوران ایجاد می‌شود که حاصل از تغییر متفیر زیر است.

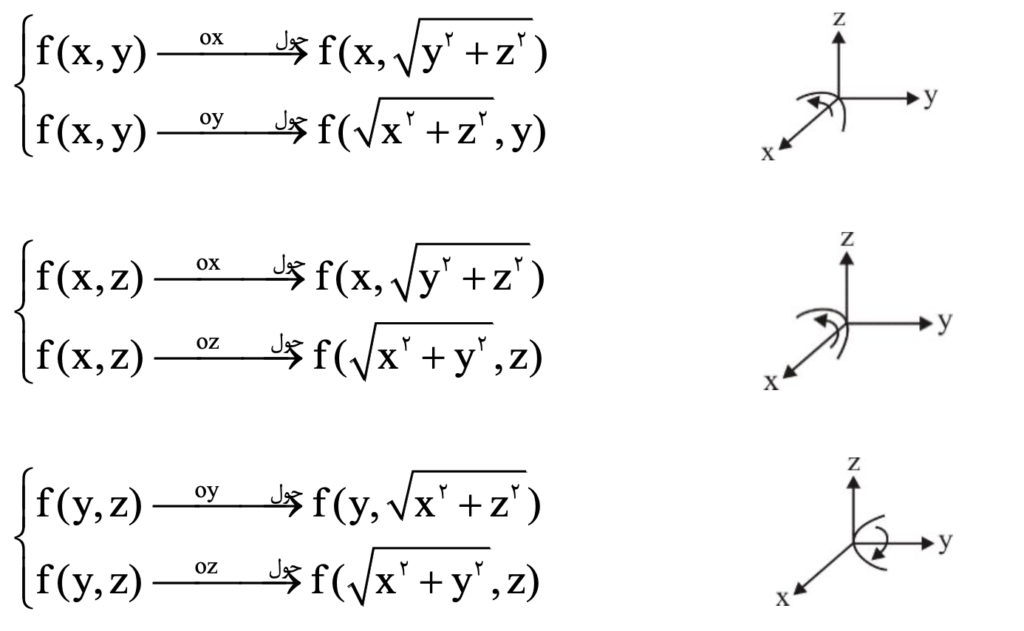
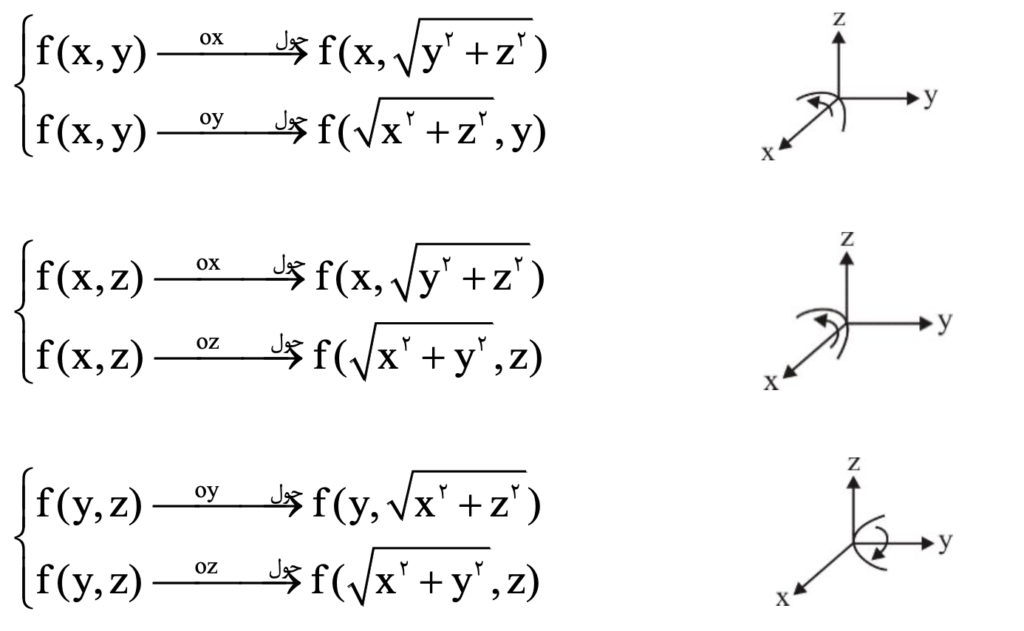
درحقیقت، در این رویه‌ها متغیر مشابه محور مختصات ثابت می‌ماند و متغیر دیگر تغییر خواهد کرد.

استوانه

استوانه‌ها در فضای سه‌بعدی ممکن است با تصور شما از استوانه یکسان نباشد. درحقیقت، چیزی که برای ما به‌عنوان استوانه شناخته می‌شود نوعی از استوانه‌ها هستند که معادله آن‌ها مشابه دایره در فضای دوبعدی است.

در حالت کلی، در فضای سه‌بعدی هر معادله‌ای که از یکی از متفیرهای x، y یا z بی‌بهره باشد رویه استوانه می‌نامند. هر استوانه موازی محوری است که متغیر آن در معادله رویه غایب است.

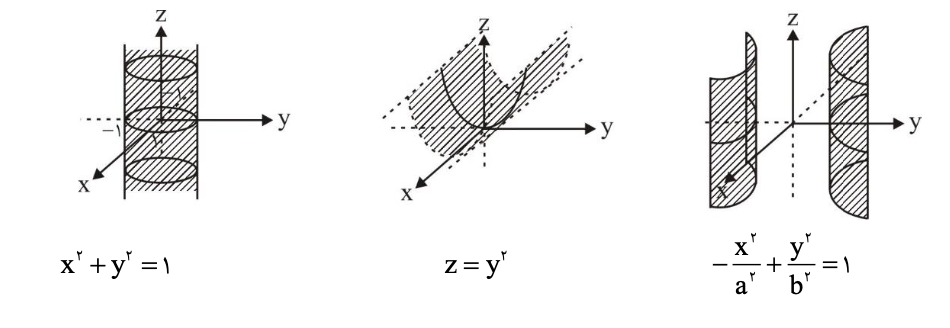
رویه‌های درجه دوم

هر معادله به این فرم اتفاق می‌افتد:

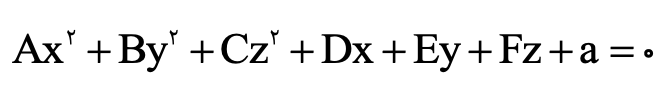
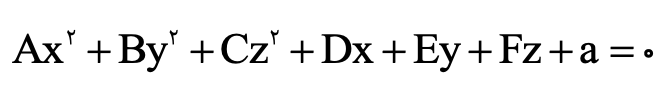
A، B و C همزمان صفر نباشند سطوح درجه دوم گوییم که مربع کامل کردن یکی از این حالت‌ها اتفاق می‌افتد:

بیضی‌گون

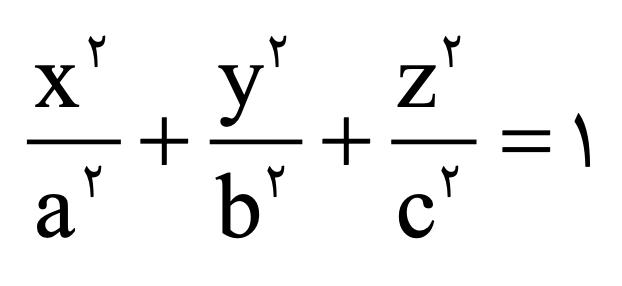
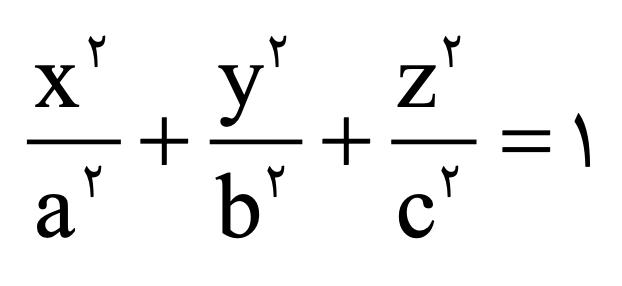
بیضی‌گون به فرم بالا خواهد بود. کره حالت خاص بیضی‌گون است که مخرج ها یکسان باشد. حجم بیضی‌گون از این قرار است:

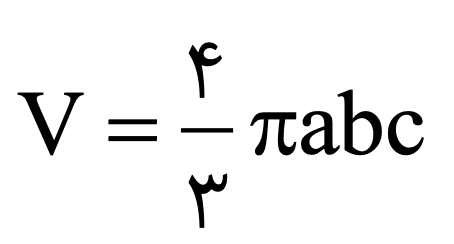
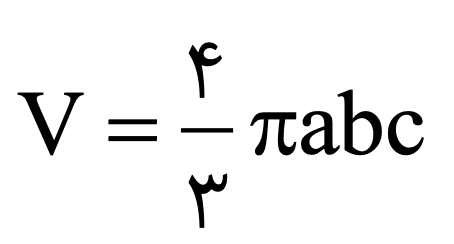
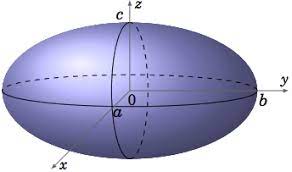
رویه بیضی گون

هذلولی‌گون

فرم هذلولی‌گون به‌این صورت است:

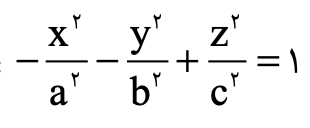
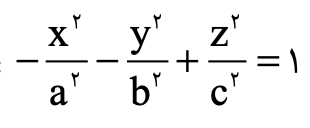
به این مدل از هذلولی‌ها دو پارچه گویند. علامت مثبت پشت هر یک از متغیرها قرار بگیرد، رویه هذلولی در همان راستا خواهد بود.

رویه هذلولی گون

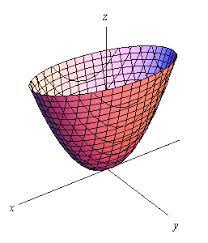
سهمی‌گون

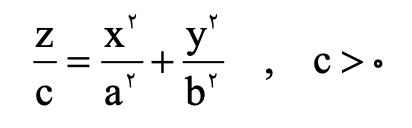
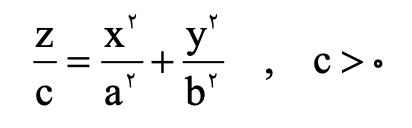
اگر در فرم استاندارد یکی از A، B و C برابر صفر باشد، فرم حاصل یک رویه سهمی‌گون  در راستای متغیر غایب درجه‌دوم است.

رویه سهمی گون

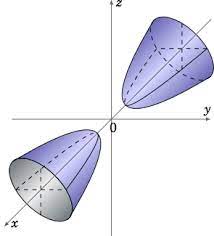
مخروط

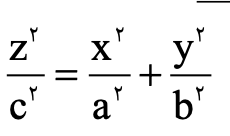
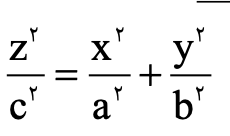
فرم کلی مخروط ها به‌این صورت است که هر یک از متغیرها به‌صورت تنها قرار گیرد، مخروط در همان راستا خواهد بود. مخروط بالا در راستا محور oz است.

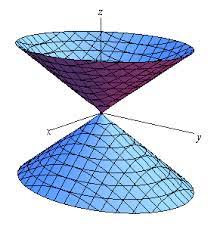
رویه مخروط

برای آشنایی با حالت‌های خاص و مکان‌های هندسی در مختصات قطبی از این قرار است:

حالات خاص و مکان‌های هندسی در مختصات قطبی

کلاس آنلاین ریاضی عمومی ۱ و ۲

برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همین‌طور رشته‌های مهندسی پیشنهاد ما شرکت در کلاس‌های آنلاین ریاضی عمومی ۱ و ۲ است.

برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

کلاس آنلاین ریاضی عمومی ۱ و ۲ رضا شکرزاد

کلاس آنلاین ریاضی عمومی ۱ و ۲ مسعود آقاسی