معرفی جامع روش‌های نمایش گراف در پایتون: از ماتریس مجاورت تا روش‌های هندسی

در دنیای پیچیده و پر از ارتباطات امروز، گراف‌ها به عنوان ابزاری قدرتمند برای نمایش و تحلیل روابط بین اجزا مطرح می‌شوند. در این مقاله، به بررسی انواع نمایش‌های گراف (Graph Representation) خواهیم پرداخت. اگر تا به حال به این فکر کرده‌اید که چگونه می‌توان ارتباطات پیچیده را به صورت ساده‌تر و قابل فهم‌تر نشان داد، این مقاله برای شماست. گراف‌ها نه تنها در علوم رایانه، بلکه در بسیاری از حوزه‌های علمی و صنعتی کاربرد دارند و درک آن‌ها می‌تواند به ما در حل مسائل پیچیده کمک کند.

نظریه گراف چیست؟

نظریه گراف (Graph Theory) شاخه‌ای از ریاضیات است که به مطالعه گراف‌ها می‌پردازد. یک گراف شامل مجموعه‌ای از رئوس (یا گره‌ها) و یال‌ها (یا لبه‌ها) است که ارتباطات بین این رئوس را نشان می‌دهد. گراف‌ها می‌توانند جهت‌دار یا بدون جهت، وزن‌دار یا بدون وزن باشند. نظریه گراف به ما این امکان را می‌دهد که ساختارها و شبکه‌های پیچیده را به صورت ساده‌تری مدل‌سازی و تحلیل کنیم. از کاربردهای نظریه گراف می‌توان به طراحی شبکه‌های کامپیوتری، تحلیل شبکه‌های اجتماعی و مدل‌سازی سیستم‌های بیولوژیکی اشاره کرد.

برای آشنایی بیشتر با نظریه گراف می‌توانید مطلب نظریه گراف: پلی بین ریاضیات و دنیای واقعی را مطالعه نمایید.

انواع نمایش گراف

یکی از مهم‌ترین جنبه‌های مطالعه گراف‌ها، نحوه نمایش آن‌ها است. نمایش گراف می‌تواند تاثیر زیادی بر کارایی الگوریتم‌ها و تحلیل‌های مختلف داشته باشد. سه نوع اصلی نمایش گراف وجود دارد: نمایش ماتریسی، نمایش لیستی و نمایش هندسی.

در نمایش ماتریسی، از ماتریس‌ها برای نشان دادن ارتباطات بین رئوس استفاده می‌شود. این روش به خصوص برای گراف‌های متراکم بسیار کارآمد است.

ماتریس مجاورت

ماتریس مجاورت (Adjacency Matrix) یکی از روش‌های نمایش گراف‌ها در نظریه گراف است. در این روش، گراف به صورت یک ماتریس مربعی نمایش داده می‌شود که نشان‌دهنده ارتباطات (یال‌ها) بین راس‌ها (گره‌ها) است. ماتریس مجاورت گراف‌های مختلف تفاوت‌هایی با هم دارند. به‌همین دلیل درادامه انواع آن را به‌تفکیک بررسی می‌کنیم:

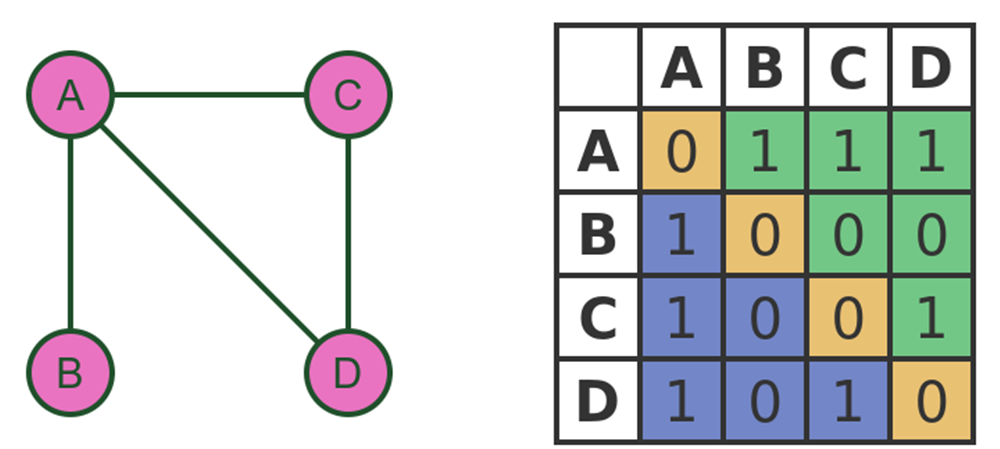
ماتریس مجاورت برای گراف‌های بی‌جهت

فرض کنید یک گراف بدون وزن و بی‌جهت G داریم که شامل n راس است. ماتریس مجاورت گراف G یک ماتریس مربعی با ابعاد n×n است که به صورت زیر تعریف می‌شود:

• هر سطر و ستون این ماتریس مربوط به یک راس از گراف است.
• اگر بین رئوس i و j یالی وجود داشته باشد، در خانه‌های (i,j) و (j,i) ماتریس مجاورت مقدار ۱ قرار می‌گیرد.
• اگر بین رئوس i و j یالی وجود نداشته باشد، در خانه‌های (i,j) و (j,i) ماتریس مجاورت مقدار ۰ قرار می‌گیرد.

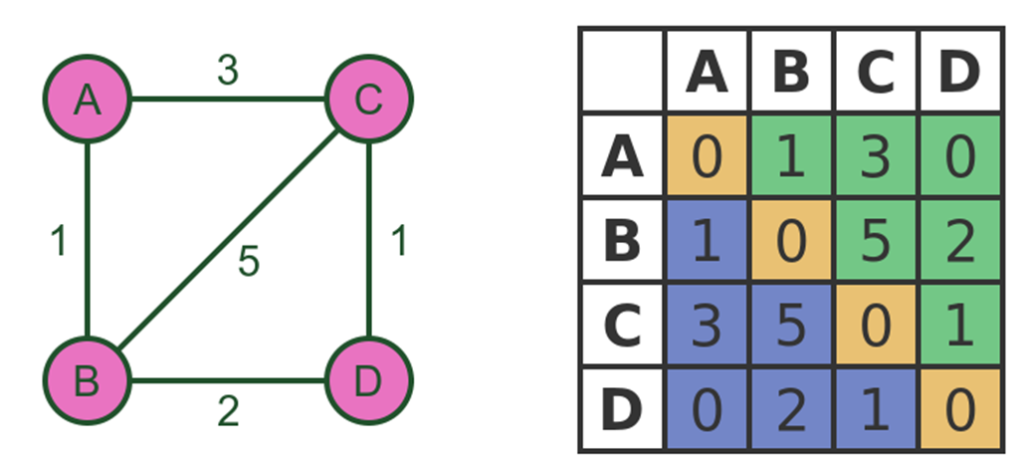
حال فرض کنید یک گراف وزن‌دار و بی‌جهت G داریم که شامل n راس است. ماتریس مجاورت گراف G یک ماتریس مربعی با ابعاد n×n است که به صورت زیر تعریف می‌شود:

• هر سطر و ستون این ماتریس مربوط به یک راس از گراف است.
• اگر بین رئوس i و j یالی وجود داشته باشد، در خانه‌های (i,j) و (j,i) ماتریس مجاورت وزن آن یال قرار می‌گیرد.
• اگر بین رئوس i و j یالی وجود نداشته باشد، در خانه‌های (i,j) و (j,i) ماتریس مجاورت مقدار ۰ یا بی‌نهایت قرار می‌گیرد.

تقارن در ماتریس مجاورت گراف بی‌جهت

در گراف‌های بی‌جهت (Undirected Graphs)، چون یال‌ها جهت ندارند، یالی که از راس i به راس j می‌رود، همان یالی است که از راس j به راس i می‌رود. بنابراین همان‌طور که در توضیحات بالا به آن اشاره شد، در ماتریس مجاورت گراف‌های بی‌جهت، رابطه A[i,j]=A[j,i] برای هر دو راسی برقرار است. این ویژگی موجب می‌شود که ماتریس مجاورت یک گراف بی‌جهت همواره متقارن باشد.

نحوه ساخت و کار با ماتریس مجاورت گراف بی‌جهت در پایتون

همان‌طور که فهمیدید، یکی از راه‌های نمایش گراف در کامپیوتر ماتریس مجاورت است. در این بخش می‌خواهیم ماتریس مجاورت گراف‌های بی‌جهت را بسازیم. برای این منظور یک کلاس به نام Graph ایجاد می‌کنیم. در متد __init__ تعداد راس‌های گراف (num_vertices) را به‌عنوان ورودی تعیین می‌کنیم و ماتریس مجاورت را با ابعاد num_vertices × num_vertices ایجاد و آن را با صفر پر می‌کنیم. متد add_edge را نیز برای افزودن یال‌ها بین راس‌ها تعریف می‌کنیم که راس‌های مبدا و مقصد یال را به‌عنوان ورودی می‌پذیرد.

دقت کنید که چون در حال ساخت ماتریس مجاورت گراف‌های بی‌جهت هستیم، یال‌ها را هم در خانه مربوط به راس مبدا و مقصد و هم در خانه متناظر که مربوط به راس مقصد و مبدا است، به ماتریس اضافه می‌کنیم. در پایان متد display را برای چاپ ماتریس مجاورت تعریف می‌کنیم:

class Graph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.num_vertices = num_vertices
        # Create an adjacency matrix to represent the graph, initialized to all zeros
        self.adj_matrix = [[0] * num_vertices for _ in range(num_vertices)]
    def add_edge(self, from_vertex, to_vertex, weight=1):
        # Add an edge between 'from_vertex' and 'to_vertex' with the specified weight
        self.adj_matrix[from_vertex][to_vertex] = weight
        self.adj_matrix[to_vertex][from_vertex] = weight
    def display(self):
        # Display the adjacency matrix row by row
        for row in self.adj_matrix:
            print(row)

در این کلاس، وزن پیش‌فرض یال‌ها در متد add_edge برابر با ۱ تعیین شده است. این بدان معنا است که اگر گرافی که می‌خواهیم آن را رسم کنیم بدون وزن باشد، نیازی به تغییر ورودی weight نداریم و تنها با تعیین رئوس یال مورد نظر می‌توان ماتریس مجاورت گراف را تشکیل داد و از آن استفاده کرد. به‌عنوان مثال، برای تعریف یک گراف بدون وزن به شکل زیر عمل می‌کنیم:

# Create an unweighted graph with 4 vertices (Nodes)
unweighted_graph = Graph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(0, 2)
unweighted_graph.add_edge(1, 3)
unweighted_graph.add_edge(2, 3)

# Display the adjacency matrix
print("Adjacency Matrix:")
unweighted_graph.display()

Adjacency Matrix:
[0, 1, 1, 0]
[1, 0, 0, 1]
[1, 0, 0, 1]
[0, 1, 1, 0]

اگر بخواهیم گراف وزن‌دار بسازیم، می‌توانیم وزن یال‌ها را به عنوان ورودی به متد add_edge بدهیم:

# Create a weighted graph with 4 vertices (Nodes)
weighted_graph = Graph(4)

# Add edges
weighted_graph.add_edge(0, 1, weight=3)
weighted_graph.add_edge(0, 2, weight=4)
weighted_graph.add_edge(1, 3, weight=5)
weighted_graph.add_edge(2, 3, weight=2)

# Display the adjacency matrix
print("Adjacency Matrix:")
weighted_graph.display()

Adjacency Matrix:
[0, 3, 4, 0]
[3, 0, 0, 5]
[4, 0, 0, 2]
[0, 5, 2, 0]

ماتریس مجاورت در گراف‌های جهت‌دار

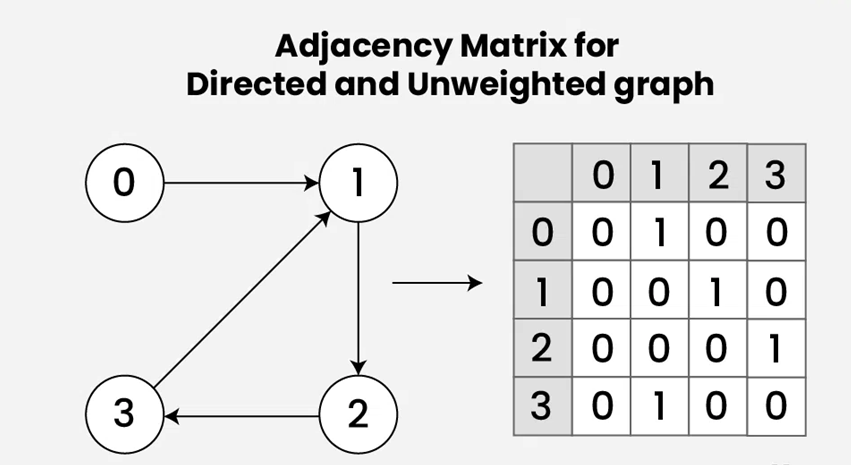
فرض کنید یک گراف بدون وزن و جهت‌دار G داریم که شامل n راس است. ماتریس مجاورت این گراف، مجددا یک ماتریس مربعی n×n است که به‌صورت زیر تعریف می‌شود:

• هر سطر و ستون این ماتریس مربوط به یک راس از گراف است.
• اگر از راس i به راس j یالی وجود داشته باشد، تنها در خانه‌ (i,j) ماتریس مجاورت مقدار ۱ قرار می‌گیرد.
• اگر از راس i به راس j یالی وجود نداشته باشد، تنها در خانه‌ (i,j) ماتریس مجاورت مقدار ۰ قرار می‌گیرد.

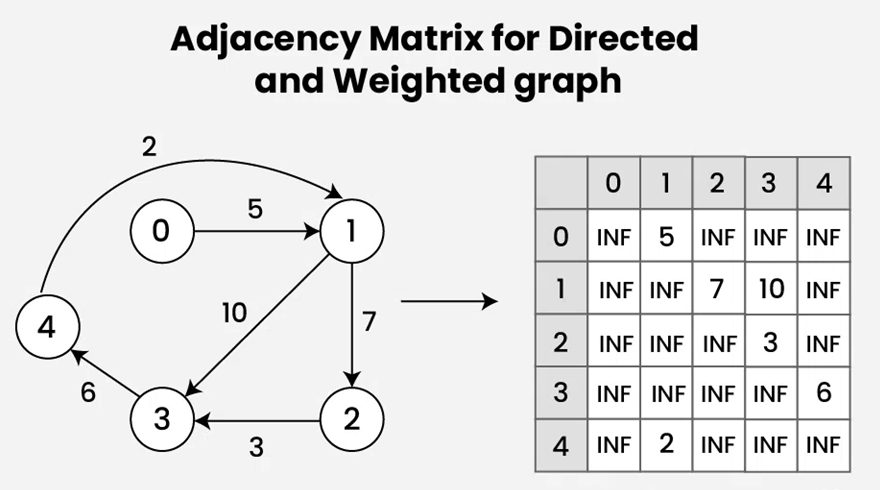
حال فرض کنید یک گراف وزن‌دار و جهت‌دار G داریم که شامل n راس است. ماتریس مجاورت گراف G یک ماتریس مربعی با ابعاد n×n است که به صورت زیر تعریف می‌شود:

• هر سطر و ستون این ماتریس مربوط به یک راس از گراف است.
• اگر بین رئوس i و j یالی وجود داشته باشد، تنها در خانه‌ (i,j) ماتریس مجاورت وزن آن یال قرار می‌گیرد.
• اگر بین رئوس i و j یالی وجود نداشته باشد، تنها در خانه‌ (i,j) ماتریس مجاورت مقدار ۰ یا بی‌نهایت قرار می‌گیرد.

عدم تقارن در ماتریس‌ مجاورت گراف جهت‌دار

در گراف‌های جهت‌دار (Directed Graphs)، هر یال دارای جهت خاصی است، یعنی اگر یالی از راس i به راس j وجود داشته باشد، این لزوماً به معنای وجود یالی از راس j به راس i نیست. بنابراین همان‌طور که در توضیحات بالا اشاره شد، ماتریس مجاورت در گراف‌های جهت‌دار معمولاً متقارن نیست و این یعنی رابطه A[i,j]=A[j,i] لزوما در آن برقرار نمی‌باشد.

نحوه ساخت و کار با ماتریس مجاورت گراف جهت‌دار در پایتون

در این بخش می‌خواهیم ماتریس مجاورت گراف‌های جهت‌دار را بسازیم. برای این منظور یک کلاس به نام DirectedGraph ایجاد می‌کنیم. در متد __init__ تعداد راس‌های گراف (num_vertices) را به‌عنوان ورودی تعیین می‌کنیم و ماتریس مجاورت را با ابعاد num_vertices × num_vertices ایجاد و آن را با صفر پر می‌کنیم. متد add_edge را نیز برای افزودن یال‌ها بین راس‌ها تعریف می‌کنیم که راس‌های مبدا و مقصد یال را به‌عنوان ورودی می‌پذیرد. دقت کنید که چون در حال ساخت ماتریس مجاورت گراف‌های جهت‌دار هستیم، در این متد یال‌ها را فقط در جهت مستقیم به ماتریس اضافه می‌کنیم و دیگر در جهت معکوس (از راس مقصد به مبدا) یالی به ماتریس اضافه نمی‌کنیم. در پایان متد display را برای چاپ ماتریس مجاورت تعریف می‌کنیم:

class DirectedGraph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.num_vertices = num_vertices
        # Create an adjacency matrix to represent the graph, initialized to all zeros
        self.adj_matrix = [[0] * num_vertices for _ in range(num_vertices)]
    def add_edge(self, from_vertex, to_vertex, weight=1):
        # Add a directed edge from 'from_vertex' to 'to_vertex' with the specified weight
        self.adj_matrix[from_vertex][to_vertex] = weight
    def display(self):
        # Display the adjacency matrix row by row
        for row in self.adj_matrix:
            print(row)

در این کلاس نیز برای تعریف یک گراف بدون وزن نیازی به تغییر ورودی weight نداریم و به شکل زیر عمل می‌کنیم:

# Create a directed graph with 4 vertices (Nodes)
unweighted_graph = DirectedGraph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(1, 0)
unweighted_graph.add_edge(1, 3)
unweighted_graph.add_edge(3, 2)

# Display the adjacency matrix
print("Adjacency Matrix:")
unweighted_graph.display()

Adjacency Matrix:
[0, 1, 0, 0]
[1, 0, 0, 1]
[0, 0, 0, 0]
[0, 0, 1, 0]

همچنین اگر بخواهیم گراف وزن‌دار بسازیم، می‌توانیم وزن یال‌ها را به عنوان ورودی به متد add_edge بدهیم:

# Create a weighted directed graph with 4 vertices (Nodes)
weighted_graph = DirectedGraph(4)

# Add edges
weighted_graph.add_edge(0, 1, weight=3)
weighted_graph.add_edge(1, 0, weight=4)
weighted_graph.add_edge(1, 3, weight=5)
weighted_graph.add_edge(2, 3, weight=2)
weighted_graph.add_edge(3, 2, weight=-1)

# Display the adjacency matrix
print("Adjacency Matrix:")
weighted_graph.display()

Adjacency Matrix:
[0, 3, 0, 0]
[4, 0, 0, 5]
[0, 0, 0, 2]
[0, 0, -1, 0]

اهمیت تقارن در ماتریس مجاورت

تقارن در ماتریس مجاورت یکی از ویژگی‌های مهم و اساسی در نظریه گراف‌ها است. این ویژگی تأثیر بسزایی در تحلیل و درک ساختار گراف‌ها دارد و نقش کلیدی در الگوریتم‌های مختلف ایفا می‌کند. در ادامه به برخی از دلایل اهمیت تقارن در ماتریس مجاورت می‌پردازیم:

ساده‌سازی تحلیل گراف‌ها

 تقارن ماتریس مجاورت در گراف‌های بدون جهت باعث ساده‌تر شدن تحلیل و الگوریتم‌های گراف می‌شود. زیرا می‌توان از خاصیت متقارن بودن استفاده کرد تا برخی محاسبات را به نصف کاهش داد.

تشخیص نوع گراف

با بررسی تقارن ماتریس مجاورت، می‌توان به‌راحتی نوع گراف را تشخیص داد. اگر ماتریس مجاورت یک گراف متقارن باشد، گراف بی‌جهت است و اگر غیر متقارن باشد، گراف احتمالاً جهت‌دار است.

صرفه‌جویی در حافظه

در پیاده‌سازی‌های عملی، تقارن در ماتریس مجاورت به صرفه‌جویی در حافظه کمک می‌کند. از آنجا که ماتریس مجاورت متقارن است، می‌توان تنها نیمی از ماتریس (نیمه بالا یا پایین) را ذخیره کرد و در صورت نیاز، نیمه دیگر را بازسازی کرد. این موضوع به‌ویژه در گراف‌های بزرگ با تعداد زیادی راس و یال اهمیت دارد.

عملیات‌های مهم با ماتریس مجاورت

عملیات‌های مختلفی می‌توانند با استفاده از ماتریس مجاورت انجام شوند که هر یک از آن‌ها در کاربردهای عملی و تئوری اهمیت ویژه‌ای دارند. در این قسمت به بررسی این عملیات‌ها می‌پردازیم:

پیدا کردن همسایگان یک راس

برای پیدا کردن همسایگان یک راس V در یک گراف بدون وزن، کافی است سطر V را در ماتریس مجاورت بررسی کنیم. ستون‌هایی که مقدار ۱ دارند نشان‌دهنده همسایگان راس V هستند. در ماتریس‌های وزن‌دار نیز درصورتی که ستون‌های مربوط به سطر V دارای عددی غیر از ۰ یا بی‌نهایت باشند، همسایه آن راس محسوب می‌شوند.  

نحوه پیدا کردن همسایگان یک راس گراف در پایتون

برای پیدا کردن همسایگان یک راس گراف به‌ کمک ماتریس مجاورت، تابع find_neighbors را ایجاد می‌کنیم. این تابع یک ماتریس مجاورت (matrix) و شماره راس (node) مورد نظر را به‌ عنوان ورودی دریافت می‌کند و لیستی از همسایگان آن راس را برمی‌گرداند. در این تابع با استفاده از حلقه for و تابع enumerate، هر درایه در سطر مربوط به راس مورد نظر (matrix[node]) بررسی می‌شود. اگر مقدار درایه غیر صفر باشد، به این معنا است که یک یال بین راس مورد نظر و راس در حال بررسی وجود دارد:

def find_neighbors(matrix, node):
    # Initialize an empty list to store the neighbors
    neighbors = []
    # Iterate over each value in the row corresponding to the given node
    for i, val in enumerate(matrix[node]):
        # If the value is not zero, it means there is an edge between 'node' and 'i'
        if val != 0:
            # Add the node 'i' to the neighbors list
            neighbors.append(i)
    # Return the list of neighbors
    return neighbors

# Create a graph with 4 vertices (Nodes)
graph = Graph(4)

# Add edges
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 3)
graph.add_edge(2, 3)

neighbors_of_0 = find_neighbors(graph.adj_matrix, 0)
print("Neighbors of Node 0:", neighbors_of_0)

Neighbors of Node 0: [1, 2]

محاسبه توان‌های ماتریس مجاورت

توان‌های مختلف ماتریس مجاورت می‌توانند اطلاعات بیشتری درباره مسیرها و ارتباطات در گراف بدهند. به عنوان مثال، توان دوم ماتریس مجاورت تعداد مسیرهای طول ۲ بین رئوس را نشان می‌دهد. برای محاسبه توان‌های ماتریس مجاورت، می‌توان از ضرب ماتریسی استفاده کرد.

نحوه محاسبه توان دوم ماتریس مجاورت در پایتون

بااستفاده از کتابخانه numpy در پایتون به‌ راحتی می‌توان توان‌های مختلف یک ماتریس را محاسبه کرد. ما نیز در اینجا باکمک این کتابخانه توان دوم ماتریس مجاورت گراف موردنظر خود را محاسبه می‌کنیم:

import numpy as np

# Create a graph with 3 vertices (Nodes)
graph = Graph(3)

# Add edges to the graph
graph.add_edge(0, 1)
graph.add_edge(1, 2)

# Display the adjacency matrix of the graph
print("Adjacency Matrix:")
graph.display()

# Convert the adjacency matrix to a NumPy array
np_graph = np.array(graph.adj_matrix)
# Compute the square of the adjacency matrix
graph_squared = np.linalg.matrix_power(np_graph, 2)

# Display the squared adjacency matrix
print("\nAdjacency Matrix Squared:")
print(graph_squared)

Adjacency Matrix:
[0, 1, 0]
[1, 0, 1]
[0, 1, 0]

Adjacency Matrix Squared:
[1, 0, 1]
[0, 2, 0]
[1, 0, 1]

ماتریسی که ما برای این منظور تعریف کردیم، نشان‌دهنده یک گراف بی‌جهت است که درآن یک‌یال بین راس ۰ و ۱ و نیز یک یال بین راس ۱ و ۲ قرار دارد. ماتریس مجاورت این گراف را به توان دو می‌رسانیم به‌این‌ترتیب مسیرهای به طول دو یال بین رئوس گراف را پیدا می‌کنیم. تفسیر ماتریس همسایگی توان دوم این گراف به‌شرح زیر است:

• درایه (۰,۰) مقدار ۱ دارد ؛ به این معنا که یک مسیر به طول دو یال از راس ۰ به خودش وجود دارد. این مسیر از راس ۰ به ۱ می‌رود و سپس به راس ۰ برمی‌گردد.
• درایه (۲,۰) مقدار ۱ دارد؛ به این معنا که یک مسیر به طول دو یال از راس ۰ به راس ۲ وجود دارد. این مسیر از راس ۰ به راس ۱ و سپس به راس ۲ می‌رود.
• درایه (۱,۱) مقدار ۲ دارد؛ به این معنا که دو مسیر به طول دو یال از راس ۱ به خودش وجود دارد. یکی از این مسیرها از راس ۱ به ۰ می‌رود و سپس به راس ۱ برمی‌گردد. همچنین یک مسیر از راس ۱ به ۲ می‌رود و سپس به راس ۱ برمی‌گردد.
• درایه (۰,۲) مقدار ۱ دارد؛ به این معنا که یک مسیر به طول دو یال از راس ۲ به راس ۰ وجود دارد. این مسیر از راس ۲ به راس ۱ و سپس به راس ۰ می‌رود.
• درایه (۲,۲) مقدار ۱ دارد؛ به این معنا که یک مسیر به طول دو یال از راس ۲ به خودش وجود دارد. این مسیر از راس ۲ به ۱ می‌رود و سپس به راس ۲ برمی‌گردد.

الگوریتم‌های مسیریابی

الگوریتم‌هایی مانند الگوریتم فلوید-وارشال برای یافتن کوتاه‌ترین مسیر بین همه جفت راس‌ها از ماتریس مجاورت استفاده می‌کنند. این الگوریتم با استفاده از توان‌های مختلف ماتریس مجاورت، کوتاه‌ترین مسیرها را پیدا می‌کند.

بررسی وجود یال بین دو راس

برای بررسی اینکه آیا بین دو راس مشخص یالی وجود دارد یا نه، کافی است مقدار مربوطه در ماتریس مجاورت را بررسی کنیم. اگر این مقدار غیرصفر باشد، یالی بین دو راس وجود دارد.

نحوه بررسی وجود یال با ماتریس مجاورت در پایتون

برای این منظور یک تابع به نام has_edge را تعریف می‌کنیم که برای بررسی وجود یال بین دو راس در یک گراف استفاده می‌شود. در این تابع، مقدار درایه مربوط به راس‌های from_vertex و to_vertex در ماتریس مجاورت بررسی می‌شود. اگر این مقدار غیر صفر باشد، نشان‌دهنده وجود یال بین این دو راس است و تابع مقدار True برمی‌گرداند. در غیر این صورت، مقدار False برمی‌گرداند:

def has_edge(matrix, from_vertex, to_vertex):
    # Check if there is an edge between 'from_vertex' and 'to_vertex'
    # If the value in the adjacency matrix is not 0, there is an edge
    return matrix[from_vertex][to_vertex] != 0

# Create a graph with 3 vertices (Nodes)
graph = Graph(3)

# Add edges to the graph
graph.add_edge(0, 1)
graph.add_edge(1, 2)

# Check if there is an edge between vertex 0 and vertex 1
edge_exists = has_edge(graph.adj_matrix, 0, 1)
print("If there is any edge:", edge_exists)

If there is any edge: True

بررسی پیچیدگی زمانی و مکانی ماتریس مجاورت

• پیچیدگی مکانی: ماتریس مجاورت نیاز به O(n²) فضای ذخیره‌سازی دارد که برای گراف‌های بسیار بزرگ، این مقدار زیاد است.
• پیچیدگی زمانی: دسترسی به یک یال خاص یا بررسی وجود یال بین دو راس در ماتریس مجاورت O(1) زمان می‌برد، اما عملیات‌هایی که نیاز به بررسی همه یال‌ها دارند می‌توانند تا O(n²) زمان ببرند.

کاربردهای ماتریس مجاورت

ماتریس مجاورت در دنیای واقعی نیز کاربردهایی دارد که در ادامه آن‌ها را بررسی می‌کنیم:

بیوانفورماتیک

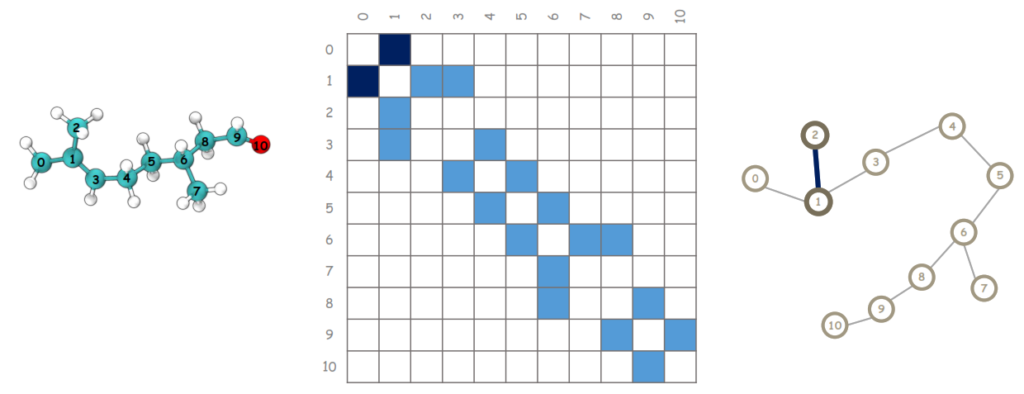
در بیوانفورماتیک، گراف‌ها برای نمایش روابط بین ژن‌ها، پروتئین‌ها یا دیگر مولکول‌های زیستی استفاده می‌شوند. ماتریس مجاورت می‌تواند برای تحلیل مسیرهای بیوشیمیایی و تعاملات مولکولی به‌کار رود. به‌عنوان مثال، می‌توان مسیرهای متابولیک، شبکه‌های تنظیم ژنی و پروتئین‌های متعامل را مدل‌سازی کرد. این تحلیل‌ها می‌توانند به درک بهتر بیماری‌ها، شناسایی هدف‌های دارویی جدید و بهینه‌سازی فرآیندهای زیستی کمک کنند.

مسائل مسیریابی و شبکه

در مسائل مسیریابی شبکه‌های کامپیوتری، جاده‌ها، و ترابری، گراف‌ها و ماتریس مجاورت برای پیدا کردن مسیرهای بهینه و تحلیل شبکه استفاده می‌شوند. با استفاده از الگوریتم‌های مختلف، می‌توان مسیرهای کوتاه‌ترین، کم‌هزینه‌ترین یا سریع‌ترین را بین دو نقطه در شبکه پیدا کرد.

تحلیل شبکه‌های ارتباطی

در شبکه‌های ارتباطی، ماتریس مجاورت می‌تواند برای مدل‌سازی و تحلیل ساختار شبکه‌های تلفنی، اینترنتی و بی‌سیم به کار رود. این تحلیل‌ها می‌توانند به بهبود کیفیت خدمات، افزایش امنیت شبکه و شناسایی گلوگاه‌های شبکه کمک کنند. به عنوان مثال، می‌توان از ماتریس مجاورت برای شناسایی نقاط ضعف در شبکه و بهینه‌سازی توزیع بار استفاده کرد. با کمک ماتریس مجاورت همچنین می‌توان نقاط بحرانی در شبکه‌های برق را شناسایی کرده و اقدامات لازم برای جلوگیری از قطع برق را انجام داد.

ماتریس درجه

ماتریس درجه (Degree Matrix)، ماتریسی است که در آن درجه هر راس در گراف نشان داده می‌شود. درجه یک راس، تعداد یال‌هایی است که به آن راس متصل است. این ماتریس برای تحلیل‌های خاصی مانند محاسبه مرکزی‌بودن راس‌ها یا یافتن راس‌های پر اتصال مفید است. ماتریس درجه به ما امکان می‌دهد تا به سرعت رئوس با تعداد ارتباطات زیاد یا کم را شناسایی کنیم و تحلیل‌های پیچیده‌تری روی ساختار گراف انجام دهیم. شیوه تعریف ماتریس درجه برای گراف‌های جهت‌دار و بی‌جهت کمی با یکدیگر متفاوت است. به‌همین دلیل این دو را جداگانه بررسی می‌کنیم:

ماتریس درجه برای گراف‌های بی‌جهت

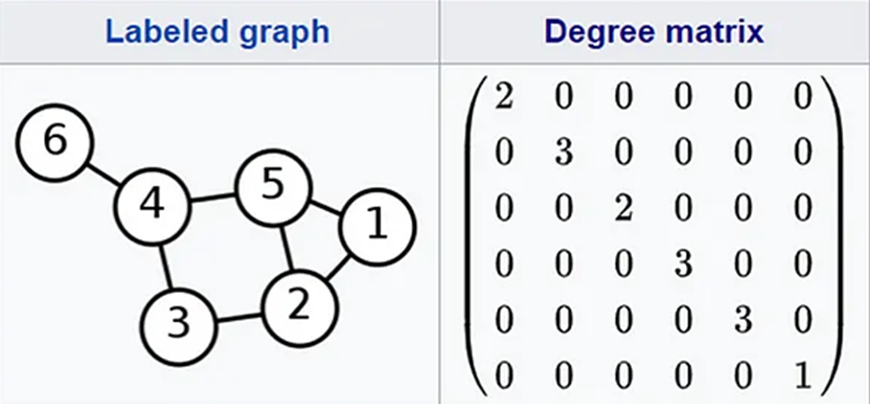
در یک گراف بدون جهت، هر راس یک درجه دارد که نشان‌دهنده تعداد یال‌های متصل به آن راس است. بنابراین، ماتریس درجه در این نوع گراف به صورت یک ماتریس قطری است که در آن تنها عناصر موجود در قطر اصلی ماتریس مقدار غیرصفر دارند.

درواقع اگر یک گراف بی‌جهت G با n راس داشته باشیم، ماتریس درجه آن یک ماتریس n×n خواهد بود که در آن هر عنصر (i, i) نشان‌دهنده تعداد یال‌های متصل به راس i است.

محاسبه ماتریس درجه در گراف بی‌جهت از روی ماتریس مجاورت

برای محاسبه ماتریس درجه در یک گراف بی‌جهت، می‌توان از ماتریس مجاورت استفاده کرد. تعداد ۱‌های موجود در هر سطر یا ستون ماتریس مجاورت برابر با درجه راس مربوطه است.

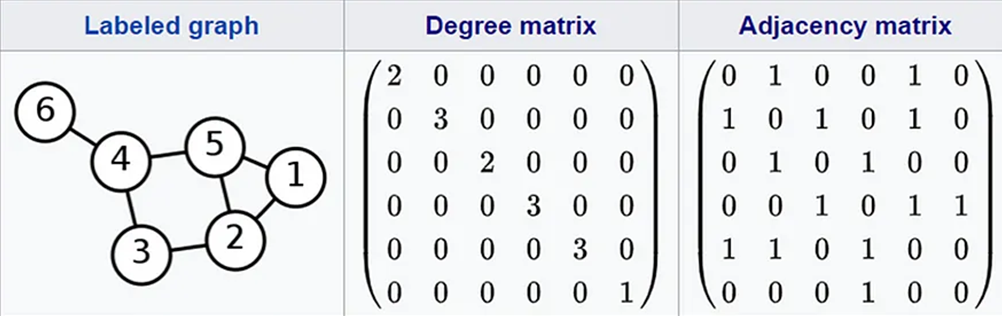
برای تحقیق این موضوع، می‌توانید در تصویر بالا اعداد هر سطح ماتریس مجاورت را جمع بزنید و حاصل را با عنصر روی قطر آن سطر در ماتریس درجه مقایسه کنید.

نحوه ساخت و کار با ماتریس درجه گراف بی‌جهت در پایتون

همان‌طور که متوجه شدید یکی از راه‌های ذخیره گراف در کامپیوتر، ماتریس درجه است. در این بخش می‌خواهیم ماتریس درجه گراف‌های بی‌جهت را در پایتون بسازیم. بری این منظور، یک کلاس به‌نام Graph ایجاد می‌کنیم. در متد __init__ این کلاس، تعداد راس‌های گراف (num_vertices) را به‌عنوان ورودی تعیین می‌کنیم و ماتریس درجه را با ابعاد num_vertices × num_vertices ایجاد و آن را با صفر پر می‌کنیم. از متد add_edge نیز استفاده می‌کنیم تا بعد از اضافه کردن هر یال، درجه رئوس مبدا و مقصد مربوط به آن یال یک واحد اضافه شود. ماتریس درجه با استفاده از این درجات ساخته می‌شود، به طوری که عناصر قطری ماتریس شامل درجه هر راس می‌باشند و بقیه عناصر صفر هستند. سپس با متد display این ماتریس درجه را به صورت سطر به سطر نمایش می‌دهیم:

class Graph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.num_vertices = num_vertices
        # Initialize the degree matrix with zeros
        self.degree_matrix = [[0] * num_vertices for _ in range(num_vertices)]
    def add_edge(self, from_vertex, to_vertex, weight=1):
        # Add an edge between 'from_vertex' and 'to_vertex'
        self.degree_matrix[from_vertex][from_vertex] += weight
        self.degree_matrix[to_vertex][to_vertex] += weight
    def display(self):
        # Display the degree matrix row by row
        for row in self.degree_matrix:
            print(row)

در این کلاس، وزن پیش‌فرض یال‌ها در متد add_edge برابر با ۱ تعیین‌شده‌است. این بدان معنا است که اگر گرافی که می‌خواهیم آن را رسم کنیم بدون وزن باشد، نیازی به تغییر ورودی weight نداریم و تنها با تعیین رئوس یال مورد نظر می‌توان ماتریس درجه گراف را تشکیل داد و از آن استفاده کرد. به‌عنوان مثال، برای تعریف ماتریس درجه یک گراف بی‌جهت و بدون وزن به شکل زیر عمل می‌کنیم:

# Create an unweighted graph with 4 vertices (Nodes)
unweighted_graph = Graph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(0, 2)
unweighted_graph.add_edge(0, 3)
unweighted_graph.add_edge(1, 2)

# Display the Degree Matrix
print("Degree Matrix:")
unweighted_graph.display()

Degree Matrix:
[3, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 2, 0]
[0, 0, 0, 1]

اگر بخواهیم ماتریس درجه یک گراف وزن‌دار را بسازیم، می‌توانیم وزن یال‌ها را به عنوان ورودی به متد add_edge بدهیم. به‌این‌ترتیب درجه هر راس باتوجه به وزن یال‌های متصل به آن محاسبه می‌شود. یعنی اگر یالی با وزن سه را بین رئوس ۰ و ۱ قرار دهیم، عنصر روی قطر سطر مربوط به هرکدام از این دو راس در ماتریس درجه، به‌جای یک واحد به‌اندازه وزن آن یال یعنی سه واحد اضافه می‌شود:

# Create a weighted graph with 4 vertices (Nodes)
weighted_graph = Graph(4)

# Add edges
weighted_graph.add_edge(0, 1, weight=2)
weighted_graph.add_edge(0, 2, weight=3)
weighted_graph.add_edge(0, 3, weight=3)
weighted_graph.add_edge(1, 2, weight=4)

# Display the Degree Matrix
print("Degree Matrix:")
weighted_graph.display()

Degree Matrix:
[8, 0, 0, 0]
[0, 6, 0, 0]
[0, 0, 7, 0]
[0, 0, 0, 3]

ماتریس درجه برای گراف‌های جهت‌دار

در یک گراف جهت‌دار، هر راس دو نوع درجه دارد: درجه ورودی (In-degree) و درجه خروجی (Out-degree). بنابراین، ماتریس درجه در این نوع گراف شامل دو ماتریس جداگانه برای درجه‌های ورودی و خروجی است. ردیف‌ها و ستون‌ها در هر دو ماتریس نمایانگر راس‌های گراف هستند، اما مقادیر موجود در ماتریس درجه ورودی تعداد یال‌هایی که به هر راس وارد می‌شوند و مقادیر موجود در ماتریس درجه خروجی تعداد یال‌هایی که از هر راس خارج می‌شوند را نشان می‌دهند.

درواقع اگر یک گراف جهت‌دار G با n راس داشته باشیم، ماتریس درجه ورودی آن یک ماتریس n×n خواهد بود که در آن هر عنصر (i, i) نشان‌دهنده تعداد یال‌های ورودی به راس i است و ماتریس درجه خروجی آن یک ماتریس n×n خواهد بود که در آن هر عنصر (i, i) نشان‌دهنده تعداد یال‌های خروجی از راس i است.

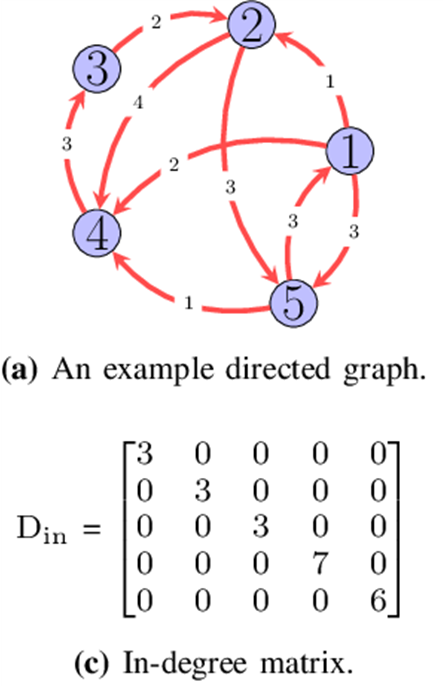
نحوه ساخت و کار با ماتریس درجه گراف جهت‌دار در پایتون

دراین بخش می‌خواهیم ماتریس درجه گراف‌های جهت‌دار را درپایتون بسازیم. برای این‌منظور، یک‌کلاس به‌نام DirectedGraph ایجاد می‌کنیم. درمتد __init__ این‌کلاس، تعداد راس‌های گراف (num_vertices) را به‌عنوان ورودی تعیین می‌کنیم و دوماتریس درجه ورودی و خروجی گراف را باابعاد num_vertices × num_vertices ایجاد و آن‌ها را باصفر پر می‌کنیم. از متد add_edge نیز استفاده می‌کنیم تا بعداز اضافه کردن هر یال، درجه رئوس مبدا درماتریس درجه خروجی و درجه رئوس مقصد درماتریس درجه ورودی مربوط به‌آن یال یک‌واحد اضافه شود. ماتریس‌های درجه بااستفاده از این‌درجات ساخته‌می‌شوند، به‌طوری که عناصر قطری ماتریس‌ درجه ورودی شامل تعداد یال‌های واردشونده به ‌هرراس می‌باشند و عناصر قطری ماتریس‌ درجه خروجی شامل تعداد یال‌های خارج‌شونده از هرراس می‌باشند. سایر درایه‌های ماتریس صفر می‌ماند. سپس بامتد display این دو ماتریس درجه را به‌صورت سطربه‌سطر نمایش می‌دهیم:

class DirectedGraph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.num_vertices = num_vertices
        # Initialize the in-degree and out-degree matrices with zeros
        self.in_degree_matrix = [[0] * num_vertices for _ in range(num_vertices)]
        self.out_degree_matrix = [[0] * num_vertices for _ in range(num_vertices)]
    def add_edge(self, from_vertex, to_vertex, weight=1):
        # Add an edge from 'from_vertex' to 'to_vertex'
        self.out_degree_matrix[from_vertex][from_vertex] += weight
        self.in_degree_matrix[to_vertex][to_vertex] += weight
    def display_in_degree_matrix(self):
        # Display the in-degree matrix row by row
        for row in self.in_degree_matrix:
            print(row)
    def display_out_degree_matrix(self):
        # Display the out-degree matrix row by row
        for row in self.out_degree_matrix:
            print(row)

در این کلاس، وزن پیش‌فرض یال‌ها در متد add_edge برابر با ۱ تعیین‌ شده‌ است. این بدان معنا است که اگر گرافی که می‌خواهیم آن را رسم کنیم بدون وزن باشد، نیازی به تغییر ورودی weight نداریم و تنها با تعیین رئوس یال مورد نظر می‌توان ماتریس‌های درجه گراف جهت‌دار را تشکیل داد و از آن استفاده کرد. به‌عنوان مثال، برای تعریف ماتریس‌های درجه یک گراف بدون وزن به‌شکل زیر عمل می‌کنیم:

# Create an unweighted graph with 4 vertices (Nodes)
unweighted_graph = DirectedGraph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(0, 2)
unweighted_graph.add_edge(0, 3)
unweighted_graph.add_edge(2, 0)

# Display the In-Degree Matrix
print("In-Degree Matrix:")
unweighted_graph.display_in_degree_matrix()
# Display the Out-Degree Matrix
print("Out-Degree Matrix:")
unweighted_graph.display_out_degree_matrix()

In-Degree Matrix:
[0, 0, 0, 0]
[0, 1, 0, 0]
[0, 0, 1, 0]
[0, 0, 0, 1]

Out-Degree Matrix:
[3, 0, 0, 0]
[0, 0, 0, 0]
[0, 0, 1, 0]
[0, 0, 0, 0]

اگر بخواهیم ماتریس‌های درجه یک گراف جهت‌دار و وزن‌دار را بسازیم، می‌توانیم وزن یال‌ها را به عنوان ورودی به متد add_edge بدهیم. به‌این‌ترتیب درجه ورودی هرراس باتوجه به‌وزن یال‌های واردشونده به‌آن و درجه خروجی هر راس باتوجه به‌وزن یال‌های خارج‌شونده از آن محاسبه می‌شود. یعنی اگر یالی با وزن سه را از راس ۰ به ۱ ببریم، عنصر روی قطر سطر ۱ در ماتریس درجه ورودی، به‌جای یک واحد به‌اندازه سه واحد و نیز عنصر روی قطر سطر ۰ در ماتریس درجه خروجی، به‌جای یک واحد به‌اندازه سه واحد اضافه می‌شود:

# Create a weighted graph with 4 vertices (Nodes)
weighted_graph = DirectedGraph(4)

# Add edges
weighted_graph.add_edge(0, 1, weight=2)
weighted_graph.add_edge(0, 2, weight=3)
weighted_graph.add_edge(2, 0, weight=4)
weighted_graph.add_edge(3, 1, weight=3)

# Display the In-Degree Matrix
print("In-Degree Matrix:")
weighted_graph.display_in_degree_matrix()
# Display the Out-Degree Matrix
print("Out-Degree Matrix:")
weighted_graph.display_out_degree_matrix()

In-Degree Matrix:
[0, 0, 0, 0]
[0, 5, 0, 0]
[0, 0, 3, 0]
[0, 0, 0, 0]

Out-Degree Matrix:
[5, 0, 0, 0]
[0, 0, 0, 0]
[0, 0, 4, 0]
[0, 0, 0, 3]

یافتن ماتریس لاپلاسی به‌کمک ماتریس‌های مجاورت و درجه

ماتریس لاپلاسی یک گراف، ماتریسی است که از تفریق ماتریس مجاورت از ماتریس درجه به‌دست می‌آید. فرمول محاسبه ماتریس لاپلاسی به صورت زیر است:

\large A - D = L

که در آن D ماتریس درجه و A ماتریس مجاورت است.

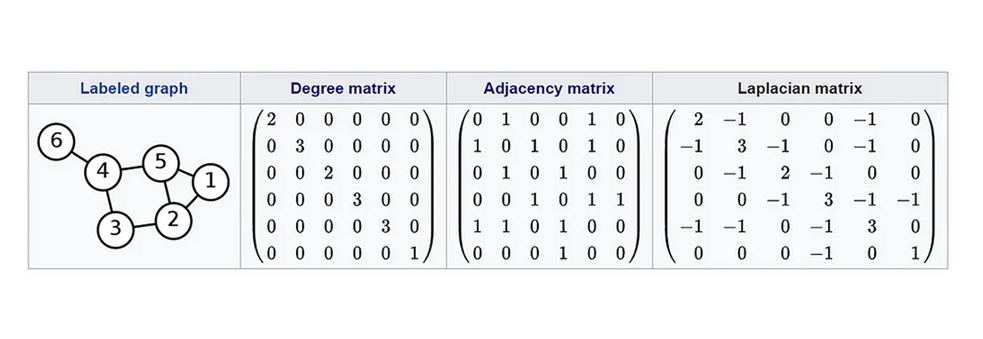
شاید بپرسید ماتریس لاپلاسی به چه دردی می‌خورد، باید بگوییم که با محاسبه مقادیر ویژه (Eigenvalues) و بردارهای ویژه (Eigenvectors) ماتریس لاپلاسی، می‌توان اطلاعات زیادی درباره ساختار گراف به‌دست آورد. به عنوان مثال، کوچکترین مقدار ویژه (که به آن مقدار ویژه صفر نیز گفته می‌شود) نشان‌دهنده تعداد مولفه‌های همبند گراف است.

بررسی پیچیدگی زمانی و مکانی ماتریس درجه

• پیچیدگی مکانی: از آنجا که ماتریس درجه یک ماتریس قطری است، فضای ذخیره‌سازی آن O(n) است، زیرا فقط عناصر قطر اصلی دارای مقدار هستند.
• پیچیدگی زمانی: محاسبه عملیات‌های مختلف بر روی ماتریس درجه معمولاً به زمان O(n) نیاز دارد، زیرا برای هر عملیات باید درجه هر راس بررسی و محاسبه شود.

کاربردهای ماتریس درجه

ماتریس درجه در دنیای واقعی نیز کاربردهایی دارد که در ادامه آن‌ها را بررسی می‌کنیم:

تحلیل شبکه‌های اجتماعی

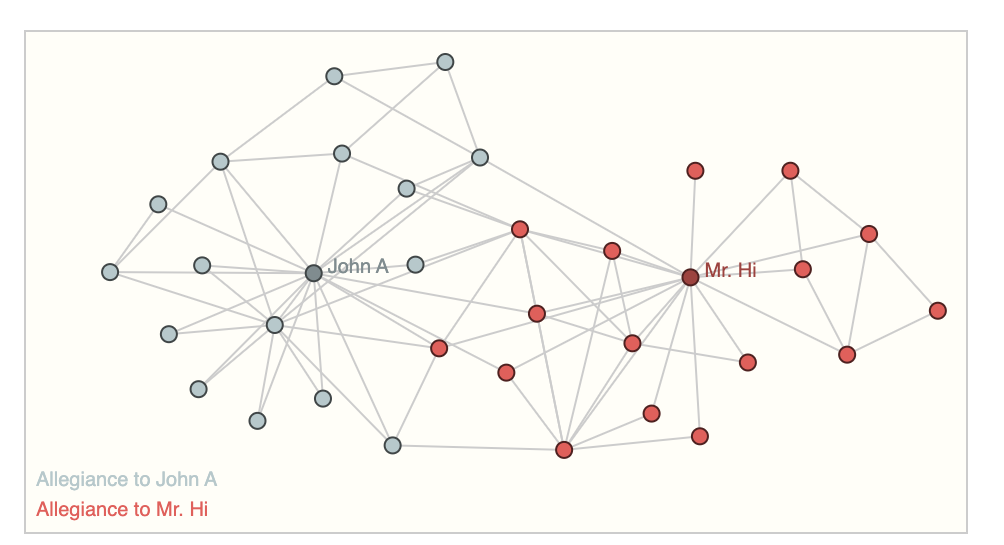
در شبکه‌های اجتماعی، ماتریس درجه می‌تواند برای تحلیل ارتباطات و تعاملات بین کاربران استفاده شود. به عنوان مثال، با استفاده از ماتریس درجه می‌توان کاربران پرتعامل را شناسایی کرد و استراتژی‌های مناسب برای افزایش تعاملات کاربران با این افراد ایجاد کرد.

تحلیل داده‌های بزرگ

ماتریس درجه در تحلیل داده‌های بزرگ و پیچیده مانند شبکه‌های ارتباطی، شبکه‌های حمل و نقل و شبکه‌های اطلاعاتی بسیار مفید است. به عنوان مثال، در شبکه‌های حمل و نقل، ماتریس درجه می‌تواند نقاط پرترافیک و پرازدحام را شناسایی کرده و راهکارهای بهینه‌سازی برای کاهش ترافیک ارائه دهد.

ماتریس رخداد

ماتریس رخداد (Incidence Matrix) ماتریسی است که نشان می‌دهد هر یال گراف به کدام راس‌ها متصل است. این ماتریس به‌ویژه برای تحلیل گراف‌های جهت‌دار و پیچیده بسیار مفید است. در ماتریس رخداد، هر سطر نمایانگر یک راس و هر ستون نمایانگر یک یال است. مانند دو ماتریس قبلی، ماتریس رخداد نیز برای گراف‌های مختلف به‌روش‌های مختلفی تعریف می‌شود. به‌همین دلیل درادامه هر یک را جداگانه بررسی خواهیم کرد:

ماتریس رخداد در گراف‌های بی‌جهت

فرض کنید یک گراف بدون وزن و بی‌جهت G داریم که شامل n راس و e یال است. ماتریس رخداد این گراف، یک ماتریس n×e است که به‌صورت زیر تعریف می‌شود:

• هر سطر این ماتریس مربوط به یک راس و هر ستونش مربوط به یک یال از گراف است.
• اگر بین رئوس i و j یال k وجود داشته باشد، مقدار ۱ درخانه‌های (i,k) و (j,k) ماتریس رخداد قرار می‌گیرد.
• اگر یال k به راس i متصل نباشد، مقدار ۰ درخانه‌ (i,k) ماتریس رخداد قرار می‌گیرد.

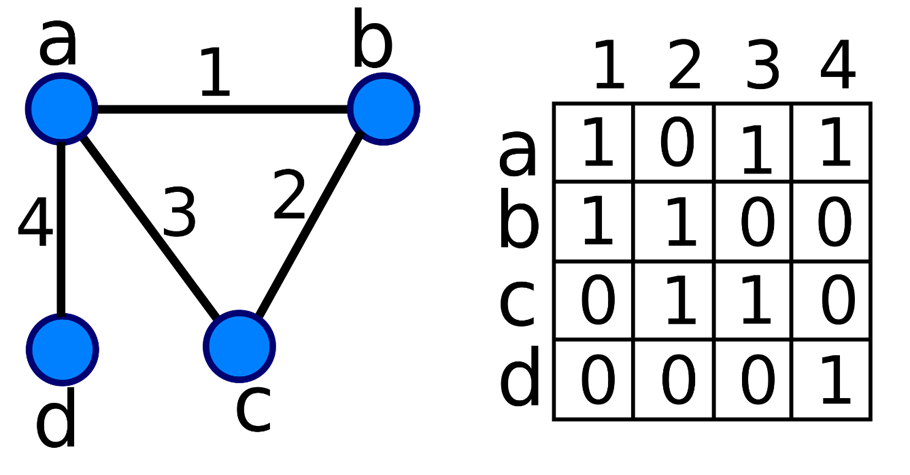
حال فرض کنید یک گراف وزن‌دار و بی‌جهت G داریم که شامل n راس و e یال است. ماتریس رخداد این گراف، یک ماتریس n×e است که به‌صورت زیر تعریف می‌شود:

• هر سطر این ماتریس مربوط به یک راس و هر ستونش مربوط به یک یال از گراف است.
• اگر بین رئوس i و j یال k وجود داشته باشد، وزن آن یال درخانه‌های (i,k) و (j,k) ماتریس رخداد قرار می‌گیرد.
• اگر یال k به راس i متصل نباشد، مقدار ۰ درخانه‌ (i,k) ماتریس رخداد قرار می‌گیرد.

نحوه ساخت و کار با ماتریس رخداد گراف بی‌جهت در پایتون

برای این منظور یک کلاس به نام Graph تعریف می‌کنیم که برای نمایش ماتریس رخداد در گراف‌های بی‌جهت استفاده می‌شود. در متد __init__ این کلاس که تعداد راس‌های گراف را به‌عنوان ورودی دریافت می‌کند، یک ماتریس رخداد خالی ایجاد می‌کنیم که به عنوان لیستی از لیست‌ها، به ازای هر راس یک لیست خالی می‌سازد و همچنین یک لیست خالی برای یال‌ها تعریف می‌کند. سپس، متد add_edge را برای افزودن یک یال بین دو راس مشخص ایجاد می‌کنیم. این متد ابتدا یال جدید را به لیست یال‌ها اضافه می‌کند و سپس ماتریس رخداد را با اضافه کردن یک ستون جدید برای یال جدید گسترش می‌دهد. این متد در نهایت، یال را به خانه‌های مربوط به ستون آن یال و سطر متناظر با راس‌ مبدا و مقصد اختصاص می‌دهد. متد display برای نمایش ماتریس رخداد به کار می‌رود و هر سطر از ماتریس را به طور جداگانه چاپ می‌کند:

class Graph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.num_vertices = num_vertices
        # Initialize the incidence matrix as an empty list
        self.incidence_matrix = [[] for _ in range(num_vertices)]
        self.edges = []
    def add_edge(self, from_vertex, to_vertex, weight=1):
        # Add an edge between 'from_vertex' and 'to_vertex' with a specified weight
        self.edges.append((from_vertex, to_vertex, weight))
        # Extend the incidence matrix to add a new column for the new edge
        for row in self.incidence_matrix:
            row.append(0)
        # Get the index of the new edge
        edge_index = len(self.edges) - 1
        # Update the incidence matrix
        self.incidence_matrix[from_vertex][edge_index] = weight
        self.incidence_matrix[to_vertex][edge_index] = weight
    def display(self):
        # Display the incidence matrix row by row
        for row in self.incidence_matrix:
            print(row)

در این کلاس، وزن پیش‌فرض یال‌ها در متد add_edge برابر با ۱ تعیین‌شده‌است. این بدان معنا است که اگر گرافی که می‌خواهیم آن را رسم کنیم بدون وزن باشد، نیازی به تغییر ورودی weight نداریم و تنها با تعیین رئوس یال مورد نظر می‌توان ماتریس رخداد گراف را تشکیل داد. به‌عنوان مثال، برای تعریف ماتریس رخداد یک گراف بی‌جهت و بدون وزن به شکل زیر عمل می‌کنیم:

# Create an unweighted graph with 4 vertices (Nodes)
unweighted_graph = Graph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(1, 2)
unweighted_graph.add_edge(1, 3)
unweighted_graph.add_edge(3, 1)
unweighted_graph.add_edge(2, 3)

# Display the Incidence Matrix
print("Incidence Matrix:")
unweighted_graph.display()

Incidence Matrix:
[1, 0, 0, 0, 0]
[1, 1, 1, 1, 0]
[0, 1, 0, 0, 1]
[0, 0, 1, 1, 1]

اگر بخواهیم ماتریس رخداد یک گراف وزن‌دار را بسازیم، می‌توانیم وزن یال‌ها را به عنوان ورودی به متد add_edge بدهیم. به‌این‌ترتیب وزن هر یال است که در ستون آن یال و سطر متناظر با راس‌ مبدا و مقصد ثبت می‌شود:

# Create a weighted graph with 4 vertices (Nodes)
weighted_graph = Graph(4)

# Add edges
weighted_graph.add_edge(0, 1, weight=2)
weighted_graph.add_edge(1, 2, weight=3)
weighted_graph.add_edge(1, 3, weight=4)
weighted_graph.add_edge(3, 1, weight=3)
weighted_graph.add_edge(2, 3, weight=3)

# Display the Incidence Matrix
print("Incidence Matrix:")
weighted_graph.display()

Incidence Matrix:
[2, 0, 0, 0, 0]
[2, 3, 4, 3, 0]
[0, 3, 0, 0, 3]
[0, 0, 4, 3, 3]

ماتریس رخداد در گراف‌های جهت‌دار

فرض کنید یک گراف بدون وزن و جهت‌دار G داریم که شامل n راس و e یال است. ماتریس رخداد این گراف، یک ماتریس n×e است که به‌صورت زیر تعریف می‌شود:

• هر سطر این ماتریس مربوط به یک راس و هر ستونش مربوط به یک یال از گراف است.
• اگر از راس i به راس j یال k وجود داشته باشد، عدد ۱ درخانه‌ (i,k) و عدد ۱- درخانه (j,k) ماتریس رخداد قرار می‌گیرد.
• اگر یال k به راس i متصل نباشد، مقدار ۰ در خانه‌ (i,k) ماتریس رخداد قرار می‌گیرد.

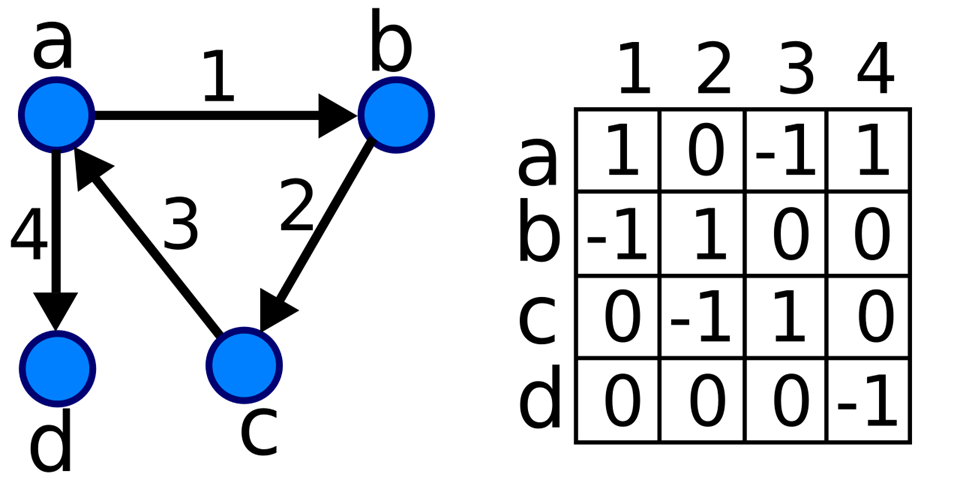
حال فرض کنید یک گراف وزن‌دار و جهت‌دار G داریم که شامل n راس و e یال است. ماتریس رخداد این گراف، یک ماتریس n×e است که به‌صورت زیر تعریف می‌شود:

• هر سطر این ماتریس مربوط به یک راس و هر ستونش مربوط به یک یال از گراف است.
• اگر از راس i به راس j یال k با وزن w وجود داشته باشد، عدد w درخانه‌ (i,k) و عدد -w درخانه (j,k) ماتریس رخداد قرار می‌گیرد.
• اگر یال k به راس i متصل نباشد، مقدار ۰ در خانه‌ (i,k) ماتریس رخداد قرار می‌گیرد.

نحوه ساخت و کار با ماتریس رخداد گراف جهت‌دار در پایتون

برای این منظور یک کلاس به نام DirectedGraph تعریف می‌کنیم که برای نمایش ماتریس رخداد در گراف‌های جهت‌دار استفاده می‌شود. در متد __init__ این کلاس که تعداد راس‌های گراف را به‌عنوان ورودی دریافت می‌کند، یک ماتریس رخداد خالی ایجاد می‌کنیم که به عنوان لیستی از لیست‌ها، به ازای هر راس یک لیست خالی می‌سازد و همچنین یک لیست خالی برای یال‌ها تعریف می‌کند.

سپس متد add_edge را برای افزودن یک یال بین دو راس مشخص ایجاد می‌کنیم. این متد ابتدا یال جدید را به لیست یال‌ها اضافه می‌کند و سپس ماتریس رخداد را با اضافه کردن یک ستون جدید برای یال جدید گسترش می‌دهد. این متد در نهایت، یال را به خانه‌های مربوط به ستون آن یال و سطر متناظر با راس مبدا (با علامت منفی، به‌معنای خروج آن یال از راس) و راس مقصد (با علامت مثبت، به‌معنای ورود آن یال به راس) اختصاص می‌دهد.

متد display برای نمایش ماتریس رخداد به کار می‌رود و هر سطر از ماتریس را به طور جداگانه چاپ می‌کند:

class DirectedGraph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.num_vertices = num_vertices
        # Initialize the incidence matrix as an empty list
        self.incidence_matrix = [[] for _ in range(num_vertices)]
        self.edges = []
    def add_edge(self, from_vertex, to_vertex, weight=1):
        # Add an edge between 'from_vertex' and 'to_vertex' with a specified weight
        self.edges.append((from_vertex, to_vertex, weight))
        # Extend the incidence matrix to add a new column for the new edge
        for row in self.incidence_matrix:
            row.append(0)
        # Get the index of the new edge
        edge_index = len(self.edges) - 1
        # Update the incidence matrix
        self.incidence_matrix[from_vertex][edge_index] = -weight # -weight for the source node
        self.incidence_matrix[to_vertex][edge_index] = weight # weight for the target node
    def display(self):
        # Display the incidence matrix row by row
        for row in self.incidence_matrix:
            print(row)

در این کلاس، وزن پیش‌فرض یال‌ها در متد add_edge برابر با ۱ تعیین‌شده‌است. این بدان معنا است که اگر گرافی که می‌خواهیم آن را رسم کنیم بدون وزن باشد، نیازی به تغییر ورودی weight نداریم و تنها با تعیین رئوس یال مورد نظر می‌توان ماتریس رخداد گراف را تشکیل داد. به‌عنوان مثال، برای تعریف ماتریس رخداد یک گراف جهت‌دار و بدون وزن به شکل زیر عمل می‌کنیم:

# Create an unweighted graph with 4 vertices (Nodes)
unweighted_graph = DirectedGraph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(1, 2)
unweighted_graph.add_edge(1, 3)
unweighted_graph.add_edge(3, 1)
unweighted_graph.add_edge(2, 3)

# Display the Incidence Matrix
print("Incidence Matrix:")
unweighted_graph.display()

Incidence Matrix:
[-1, 0, 0, 0, 0]
[1, -1, -1, 1, 0]
[0, 1, 0, 0, -1]
[0, 0, 1, -1, 1]

اگر بخواهیم ماتریس رخداد گراف وزن‌داری را بسازیم، می‌توانیم وزن یال‌ها را به عنوان ورودی به متد add_edge بدهیم. به‌این‌ترتیب وزن هر یال است که در ستون آن یال و سطر متناظر با راس مبدا (با علامت منفی) و مقصد (با علامت مثبت) ثبت می‌شود:

# Create a weighted graph with 4 vertices (Nodes)
weighted_graph = DirectedGraph(4)

# Add edges
weighted_graph.add_edge(0, 1, weight=2)
weighted_graph.add_edge(1, 2, weight=3)
weighted_graph.add_edge(1, 3, weight=4)
weighted_graph.add_edge(3, 1, weight=2)
weighted_graph.add_edge(2, 3, weight=3)

# Display the Incidence Matrix
print("Incidence Matrix:")
weighted_graph.display()

Incidence Matrix:
[-2, 0, 0, 0, 0]
[2, -3, -4, 2, 0]
[0, 3, 0, 0, -3]
[0, 0, 4, -2, 3]

عملیات‌های مهم با ماتریس رخداد

ماتریس رخداد یکی از ابزارهای مهم در نظریه گراف‌ها است که بسیاری از عملیات‌ها و تحلیل‌ها را ساده‌تر و کارآمدتر می‌کند. در این بخش به برخی از مهم‌ترین عملیات‌هایی که می‌توان با ماتریس رخداد انجام داد، می‌پردازیم:

تعیین درجه راس‌ها

در گراف‌های بدون جهت، درجه هر راس برابر است با مجموع مقادیر سطر مربوط به آن راس. در این نوع گراف‌ها، هر یال به دو راس متصل است و به همین دلیل ستون مربوط به آن یال در سطر متناظر با هر دو راس دارای مقادیر برابر است. به عنوان مثال، اگر در ماتریس رخداد یک گراف بدون جهت، در سطر مربوط به راس i و ستون e مقدار ۱ ثبت شده باشد، نشان‌دهنده این است که یالی به راس i متصل است. برای محاسبه درجه راس i، تمامی این مقادیر مطلق در سطر مربوط به i، با هم جمع می‌شوند.

نحوه تعیین درجه راس‌های گراف بی‌جهت در پایتون

برای انجام این کار یک تابع به نام calculate_degrees تعریف می‌کنیم که درجه هر راس در یک گراف بدون جهت را با جمع کردن مقادیر مطلق در هر سطر از ماتریس رخداد محاسبه می‌کند:

def calculate_degrees(matrix):
    # Calculate degrees of each vertex by summing absolute values in each row
    degrees = [sum(abs(x) for x in row) for row in matrix]
    return degrees

# Create a graph with 4 vertices (Nodes)
graph = Graph(4)

# Add edges
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
graph.add_edge(2, 3)

# Display the Incidence Matrix
print("Incidence Matrix:")
graph.display()

# Display the Degrees of vertices
degrees = calculate_degrees(graph.incidence_matrix)
print("\nDegrees of vertices:", degrees)

Incidence Matrix:
[1, 1, 0, 0]
[1, 0, 1, 0]
[0, 1, 1, 1]
[0, 0, 0, 1]

Degrees of vertices: [2, 2, 3, 1]

در یک گراف جهت‌دار، تعیین درجه ورودی (in-degree) و درجه خروجی (out-degree) هر راس یکی از عملیات‌های اساسی است که می‌توان با استفاده از ماتریس رخداد انجام داد. درجه ورودی یک راس برابر است با مجموع مقادیر مثبت در سطر مربوط به آن راس. این مقادیر مثبت نشان‌دهنده یال‌هایی هستند که به راس مورد نظر وارد می‌شوند. از طرف دیگر، درجه خروجی برابر است با مجموع قدر مطلق مقادیر منفی در سطر مربوط به آن راس. مقادیر منفی نشان‌دهنده یال‌هایی هستند که از راس مورد نظر خارج می‌شوند.

نحوه تعیین درجه راس‌های گراف جهت‌دار در پایتون

این کد یک تابع به نام calculate_degrees تعریف می‌کنیم که درجه ورودی و خروجی هر راس در یک گراف جهت‌دار را محاسبه می‌کند. درجه ورودی یک راس با جمع کردن مقادیر مثبت در هر سطر ماتریس رخداد و درجه خروجی با جمع کردن مقادیر مطلق منفی محاسبه می‌شود:

def calculate_degrees(matrix):
    # Calculate in-degrees by summing positive values in each row
    in_degrees = [sum(x for x in row if x > 0) for row in matrix]
    # Calculate out-degrees by summing absolute values of negative values in each row
    out_degrees = [sum(-x for x in row if x < 0) for row in matrix]
    return in_degrees, out_degrees

# Create a graph with 4 vertices (Nodes)
graph = DirectedGraph(4)

# Add edges
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
graph.add_edge(2, 3)

# Display the Incidence Matrix
print("Incidence Matrix:")
graph.display()

# Display the Degrees of vertices
degrees = calculate_degrees(graph.incidence_matrix)
print("\nDegrees of vertices:", degrees)

Incidence Matrix:
[-1, -1, 0, 0]
[1, 0, -1, 0]
[0, 1, 1, -1]
[0, 0, 0, 1]

Degrees of vertices: ([0, 1, 2, 1], [2, 1, 1, 0])

تعیین یال‌های بین راس‌ها

با بررسی مقادیر غیر صفر در ستون‌های ماتریس رخداد، می‌توان یال‌های موجود بین راس‌ها را شناسایی کرد. هر ستون در ماتریس رخداد نمایانگر یک یال است و مقادیر موجود در این ستون نشان‌دهنده راس‌هایی هستند که این یال به آن‌ها متصل است. در گراف‌های جهت‌دار، مقدار منفی در یک ستون نشان‌دهنده راس مبدا و مقدار مثبت نشان‌دهنده راس مقصد است. این مقادیر به ما کمک می‌کنند تا جهت یال‌ها را نیز تشخیص دهیم.

نحوه تعیین یال‌های بین راس‌های گراف بی‌جهت در پایتون

برای تعیین یال‌های بین رئوس یک گراف بی‌جهت به‌کمک ماتریس رخداد، یک تابع به‌نام get_edges تعریف می‌کنیم که ماتریس رخداد را به عنوان ورودی می‌گیرد و لیستی از یال‌ها را از آن استخراج می‌کند. این تابع ابتدا تعداد یال‌ها (num_edges) و تعداد راس‌ها (num_vertices) را از ابعاد ماتریس رخداد استخراج می‌کند. سپس با استفاده از یک حلقه for، هر ستون از ماتریس رخداد که نمایانگر یک یال است را بررسی می‌کند. برای هر ستون، تمام سطرها (یعنی راس‌ها) را پیمایش می‌کند و اگر مقدار خانه‌ای در آن ستون مثبت باشد، نشان‌دهنده این است که یال مورد نظر به آن راس متصل است. سپس راس‌های متصل به هر یال را در لیستی به نام vertices ذخیره می‌کند. اگر تعداد عناصر این لیست برابر با ۲ باشد، به این معنی است که یک یال بین این دو راس قرار دارد و این یال به لیست edges اضافه می‌شود:

def get_edges(incidence_matrix):
    # An empty list to store edges
    edges = []
    # Get the number of edges
    num_edges = len(incidence_matrix[0])
    # Get the number of vertices
    num_vertices = len(incidence_matrix)
    for j in range(num_edges):
        # An empty list to store vertices
        vertices = []
        # Iterate over each vertex
        for i in range(num_vertices):
            # Check if the vertex is connected by the edge
            if incidence_matrix[i][j] > 0:
                vertices.append(i)
        # If two vertices are connected by the edge, add the edge to the list
        if len(vertices) == 2:
            edges.append((vertices[0], vertices[1]))
    return edges

# Create a graph with 4 vertices (Nodes)
graph = Graph(4)

# Add edges
graph.add_edge(0, 1)
graph.add_edge(0, 2)
graph.add_edge(1, 2)
graph.add_edge(2, 3)
graph.add_edge(1, 3)

# Display the Incidence Matrix
print("Incidence Matrix:")
graph.display()

# Display the Edges in the graph
edges = get_edges(graph.incidence_matrix)
print("\nEdges in the graph:", edges)

Incidence Matrix:
[1, 1, 0, 0, 0]
[1, 0, 1, 0, 1]
[0, 1, 1, 1, 0]
[0, 0, 0, 1, 1]

Edges in the graph: [(0, 1), (0, 2), (1, 2), (2, 3), (1, 3)]

نحوه تعیین یال‌های بین راس‌های گراف جهت‌دار در پایتون

برای این منظور بازهم یک تابع به‌نام get_edges تعریف می‌کنیم. این تابع ابتدا تعداد یال‌ها (num_edges) و تعداد راس‌ها (num_vertices) را از ابعاد ماتریس رخداد استخراج می‌کند. سپس با استفاده از یک حلقه for، هر ستون از ماتریس رخداد که نمایانگر یک یال است را بررسی می‌کند. برای هر ستون (هر یال)، تمام سطرها (راس‌ها) را پیمایش می‌کند. اگر مقدار خانه‌ای در آن ستون منفی باشد، نشان‌دهنده این است که یال از آن راس شروع می‌شود (from_vertex) و اگر مقدار خانه‌ای مثبت باشد، نشان‌دهنده این است که یال به آن راس می‌رسد (to_vertex). پس از پیمایش هر ستون، اگر هر دو راس مبدا و مقصد یال شناسایی شده باشند، این یال به لیست edges اضافه می‌شود:

def get_edges(incidence_matrix):
    # An empty list to store edges
    edges = []
    # Get the number of edges
    num_edges = len(incidence_matrix[0])
    # Get the number of vertices
    num_vertices = len(incidence_matrix)
    for j in range(num_edges):
        from_vertex = None
        to_vertex = None
        # Iterate over each vertex
        for i in range(num_vertices):
            if incidence_matrix[i][j] < 0:
                # Identify the source vertex (negative weight)
                from_vertex = i
            elif incidence_matrix[i][j] > 0:
                # Identify the target vertex (positive weight)
                to_vertex = i
        # If both source and target vertices are identified, add the edge to the list
        if from_vertex is not None and to_vertex is not None:
            edges.append((from_vertex, to_vertex))
    return edges

# Create a graph with 4 vertices (Nodes)
graph = DirectedGraph(4)

# Add edges
graph.add_edge(0, 1)
graph.add_edge(2, 0)
graph.add_edge(1, 2)
graph.add_edge(2, 3)

# Display the Incidence Matrix
print("Incidence Matrix:")
graph.display()

# Display the Edges in the graph
edges = get_edges(graph.incidence_matrix)
print("\nEdges in the graph:", edges)

Incidence Matrix:
[-1, 1, 0, 0]
[1, 0, -1, 0]
[0, -1, 1, -1]
[0, 0, 0, 1]

Edges in the graph: [(0, 1), (2, 0), (1, 2), (2, 3)]

تعیین مسیرها و حلقه‌ها

با استفاده از ماتریس رخداد و عملیات ماتریسی می‌توان مسیرها و حلقه‌های موجود در گراف را شناسایی کرد. به عنوان مثال، برای یافتن یک مسیر بین دو راس مشخص، می‌توانیم از ماتریس رخداد استفاده کرده و با بررسی مقادیر موجود در سطرهای مربوط به این راس‌ها، مسیرهای ممکن را شناسایی کنیم.

برای شناسایی حلقه‌ها نیز می‌توان از ماتریس رخداد بهره برد. حلقه‌ها مسیرهایی هستند که از یک راس شروع شده و به همان راس بازمی‌گردند. با بررسی مقادیر موجود در ماتریس رخداد و انجام تحلیل‌های ماتریسی، می‌توان حلقه‌های موجود در گراف را شناسایی و تحلیل کرد.

بررسی پیچیدگی زمانی و مکانی ماتریس رخداد

• پیچیدگی مکانی: از آنجا که ماتریس رخداد به جای رئوس و یال‌ها شامل تمامی رئوس و یال‌های گراف است، فضای ذخیره‌سازی آن O(n + e) است، زیرا تمامی رئوس (n) و یال‌ها (e) باید در ماتریس ذخیره شوند.
• پیچیدگی زمانی: محاسبه عملیات‌های مختلف بر روی ماتریس رخداد معمولاً به زمان O(n * e) نیاز دارد، زیرا برای هر عملیات باید تمامی رئوس و یال‌های گراف بررسی شوند.

کاربردهای ماتریس رخداد

ماتریس رخداد یکی از ابزارهای مهم در نظریه گراف‌ها و شبکه‌ها است که کاربردهای فراوانی در علوم مختلف دارد. در ادامه به برخی از مهم‌ترین کاربردهای این ماتریس می‌پردازیم:

مدارهای الکتریکی

در مهندسی برق، ماتریس رخداد برای تحلیل مدارهای الکتریکی استفاده می‌شود. این ماتریس نشان‌دهنده اتصالات میان عناصر مختلف مدار مانند مقاومت‌ها، خازن‌ها و سیم‌ها است. با استفاده از ماتریس رخداد می‌توان به تحلیل جریان‌ها و ولتاژها در مدار پرداخت و معادلات کیرشهف را حل کرد.

طراحی شبکه‌های حمل و نقل

ماتریس رخداد در طراحی و تحلیل شبکه‌های حمل و نقل نیز کاربرد دارد. این ماتریس می‌تواند نشان‌دهنده ارتباطات میان نقاط مختلف در یک شبکه حمل و نقل باشد. با استفاده از این ماتریس می‌توان بهینه‌سازی مسیرها، تحلیل ترافیک و مدیریت منابع حمل و نقل را انجام داد.

طراحی سیستم‌های مکانیکی

در مهندسی مکانیک، ماتریس رخداد برای مدل‌سازی و تحلیل سازه‌های مکانیکی استفاده می‌شود. این ماتریس می‌تواند نشان‌دهنده ارتباطات میان عناصر مختلف یک سازه مانند تیرها، ستون‌ها و اتصالات باشد. با استفاده از این ماتریس می‌توان تحلیل تنش‌ها و تغییر شکل‌ها در سازه‌ها را انجام داد.

همان‌طور که گفتیم، به‌جز نمایش‌های ماتریسی می‌توان از لیست نیز برای نمایش گراف استفاده کرد. در نمایش لیستی، ارتباطات بین رئوس به صورت لیست‌هایی از یال‌ها ذخیره می‌شوند. این روش برای گراف‌های پراکنده که تعداد یال‌های کمی نسبت به تعداد رئوس دارند، بسیار مناسب است.

لیست مجاورت

در لیست مجاورت (Adjacency List)، برای هر راس یک لیست از رئوس همسایه آن نگهداری می‌شود. این روش به خصوص برای گراف‌های بزرگ و پراکنده مفید است، زیرا فضای کمتری را نسبت به ماتریس مجاورت اشغال می‌کند و دسترسی به همسایگان یک راس خاص سریع‌تر است. لیست مجاورت برای گراف‌های مختلف به‌روش‌های مختلفی تعریف می‌شود. به‌همین دلیل درادامه هر یک را جداگانه بررسی خواهیم کرد:

لیست مجاورت برای گراف‌های جهت‌دار

فرض کنید یک گراف بی‌وزن و بی‌جهت G داریم که شامل n راس و e یال است. لیست مجاورت این گراف به صورت زیر تعریف می‌شود:

• هر راس یک لیست از رئوس مجاور خود دارد.
• اگر بین رئوس i و j یال وجود داشته باشد، راس j به لیست مجاورت راس i و راس i به لیست مجاورت راس j اضافه می‌شود.

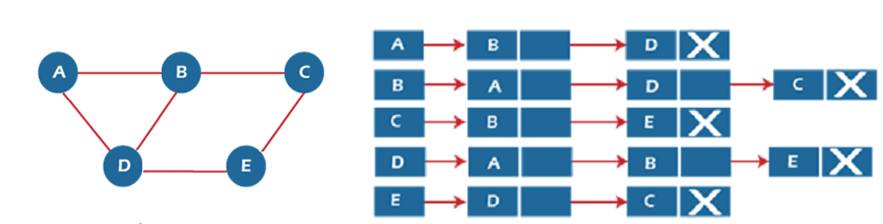
حال فرض کنید یک گراف وزن‌دار و بی‌جهت G داریم که شامل n راس و e یال است. لیست مجاورت این گراف به صورت زیر تعریف می‌شود:

• هر راس یک لیست از رئوس مجاور خود دارد.
• اگر بین رئوس i و j یالی وجود داشته باشد، راس j به‌همران وزن آن یال به لیست مجاورت راس i و راس i به‌همران وزن آن یال به لیست مجاورت راس j اضافه می‌شود.

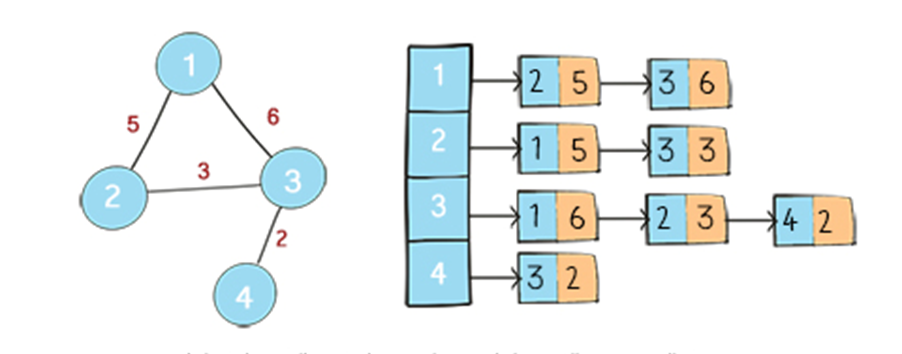
نحوه ساخت و کار با لیست مجاورت گراف بی‌جهت در پایتون

برای این منظور، یک کلاس به نام Graph تعریف می‌کنیم که برای نمایش لیست مجاورت در گراف‌های جهت‌دار استفاده می‌شود. در متد __init__ این کلاس، تعداد رئوس گراف (num_vertices) را به‌عنوان ورودی تعیین و یک لیست از مقادیر None ایجاد می‌کنیم که هر کدام نشان‌دهنده ابتدای یک لیست پیوندی (Linked List) است که برای نگهداری رئوس مجاور استفاده می‌شود. همچنین، متغیر weight را برای تعیین وزن‌دار بودن یا نبودن گراف تعریف می‌کنیم.

سپس، متد add_edge را برای افزودن یک یال بین دو راس مشخص ایجاد می‌کنیم.  در این متد، یک یال بین دو راس v1  و v2  اضافه می‌شود. سپس، گره جدید به ابتدای لیست پیوندی مجاورت اضافه می‌شود. این عملیات برای هر دو راس v1 و v2 تکرار می‌شود تا هرکدام از رئوس به لیست دیگری اضافه شود.

درپایان، متد display برای نمایش لیست مجاورت به کار می‌رود و هر لیست پیوندی را به طور جداگانه چاپ می‌کند. در صورتی که گراف وزن‌دار باشد، وزن هر یال نیز نمایش داده می‌شود:

class GraphNode:
    def __init__(self, vertex, weight=None):
        # Initialize a graph node with the given vertex and optional weight
        self.vertex = vertex
        self.weight = weight
        self.next = None

class Graph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.V = num_vertices
        # Create an adjacency list with None values for each vertex
        self.adj_list = [None] * num_vertices
        # Initialize a flag to check if the graph is weighted
        self.weighted = False

    def add_edge(self, v1, v2, weight=None):
        # Add an edge between 'v1' and 'v2' with an optional weight
        if weight is not None:
            self.weighted = True
            new_node = GraphNode(v2, weight)
        else:
            new_node = GraphNode(v2)
        # Add the new node to the adjacency list of 'v1'
        new_node.next = self.adj_list[v1]
        self.adj_list[v1] = new_node

        # Repeat the process for 'v2' to ensure undirected behavior
        if weight is not None:
            new_node = GraphNode(v1, weight)
        else:
            new_node = GraphNode(v1)
        # Add the new node to the adjacency list of 'v2'
        new_node.next = self.adj_list[v2]
        self.adj_list[v2] = new_node

    def display(self):
        # Display the adjacency list of the graph
        for i in range(self.V):
            print(f"Vertex {i}:", end="")
            temp = self.adj_list[i]
            while temp:
                # Print the vertex and weight if the graph is weighted
                if self.weighted and temp.weight is not None:
                    print(f" -> ({temp.vertex}, {temp.weight})", end="")
                else:
                    print(f" -> {temp.vertex}", end="")
                temp = temp.next
            print()

برای نمایش لیست مجاورت یک گراف بدون وزن و بی‌جهت به‌صورت زیر عمل می‌کنیم:

# Create an unweighted graph
unweighted_graph = Graph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(1, 2)
unweighted_graph.add_edge(1, 3)
unweighted_graph.add_edge(2, 3)

# Display the Adjacency list
print("Adjacency list:")
unweighted_graph.display()

Adjacency list:
Vertex 0: -> 1
Vertex 1: -> 3 -> 2 -> 0
Vertex 2: -> 3 -> 1
Vertex 3: -> 2 -> 1

برای نمایش لیست مجاورت یک گراف وزن‌دار و بی‌جهت نیز به‌شکل زیر عمل می‌کنیم:

# Create a weighted graph
graph = Graph(4)

# Add edges
graph.add_edge(0, 1, 2)
graph.add_edge(1, 2, 4)
graph.add_edge(1, 3, 3)
graph.add_edge(2, 3, 5)

# Display the Adjacency list
print("Adjacency list:")
graph.display()

Adjacency list:
Vertex 0: -> (1, 2)
Vertex 1: -> (3, 3) -> (2, 4) -> (0, 2)
Vertex 2: -> (3, 5) -> (1, 4)
Vertex 3: -> (2, 5) -> (1, 3)

لیست مجاورت برای گراف‌های جهت‌دار

حال فرض کنید یک گراف بی‌وزن و جهت‌دار G داریم که شامل n راس و e یال است. لیست مجاورت این گراف به صورت زیر تعریف می‌شود:

• هر راس یک لیست از رئوس مجاور خود دارد.
• اگر از راس i به راس j یالی وجود داشته باشد، تنها راس j به لیست مجاورت راس i اضافه می‌شود.

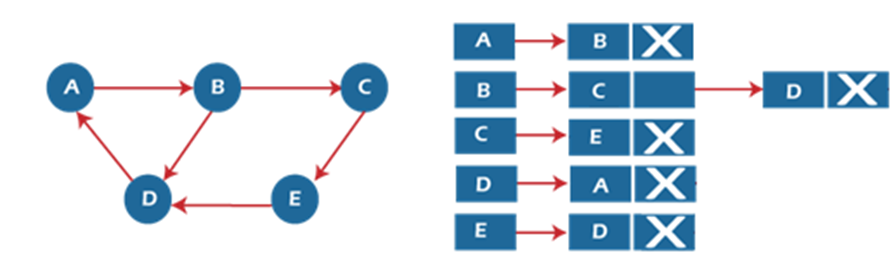
حال فرض کنید یک گراف وزن‌دار و جهت‌دار G داریم که شامل n راس و e یال است. لیست مجاورت این گراف به صورت زیر تعریف می‌شود:

• هر راس یک لیست از رئوس مجاور خود دارد.
• اگر از راس i به راس j یالی وجود داشته باشد، تنها راس j به‌همران وزن آن یال به لیست مجاورت راس i اضافه می‌شود.

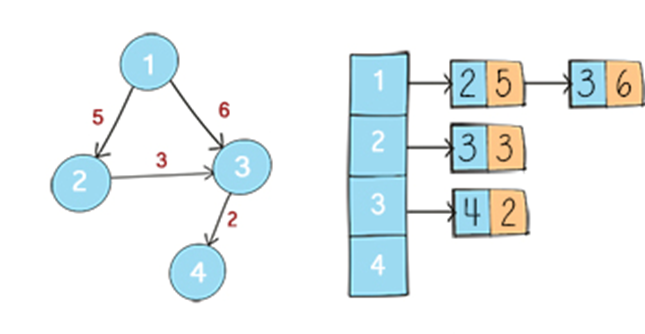
نحوه ساخت و کار با لیست مجاورت گراف جهت‌دار در پایتون

برای این منظور، یک کلاس به نام DirectedGraph تعریف می‌کنیم که برای نمایش لیست مجاورت در گراف‌های جهت‌دار استفاده می‌شود. در متد __init__ این کلاس، تعداد رئوس گراف (num_vertices) را به‌عنوان ورودی تعیین و یک لیست از مقادیر None ایجاد می‌کنیم که هر کدام نشان‌دهنده ابتدای یک لیست پیوندی است که برای نگهداری رئوس مجاور استفاده می‌شود. همچنین، متغیر weight را برای تعیین وزن‌دار بودن یا نبودن گراف تعریف می‌کنیم.

سپس، متد add_edge را برای افزودن یک یال جهت‌دار از یک راس به راس دیگر مشخص ایجاد می‌کنیم. در این متد، یک یال جهت‌دار از راس v1 به راس v2 اضافه می‌شود. سپس، گره جدید به ابتدای لیست پیوندی مجاورت اضافه می‌شود. در گراف‌های جهت‌دار، فقط v2 به لیست راس v1 اضافه می‌شود و نیازی به تکرار عملیات برای v2 نیست.

درپایان، متد display برای نمایش لیست مجاورت به کار می‌رود و هر لیست پیوندی را به طور جداگانه چاپ می‌کند. در صورتی که گراف وزن‌دار باشد، وزن هر یال نیز نمایش داده می‌شود:

class GraphNode:
    def __init__(self, vertex, weight=None):
        # Initialize a graph node with the given vertex and optional weight
        self.vertex = vertex
        self.weight = weight
        self.next = None

class DirectedGraph:
    def __init__(self, num_vertices):
        # Initialize the graph with a specified number of vertices
        self.V = num_vertices
        # Create an adjacency list with None values for each vertex
        self.adj_list = [None] * num_vertices
        # Initialize a flag to check if the graph is weighted
        self.weighted = False

    def add_edge(self, v1, v2, weight=None):
        # Add an edge from 'v1' to 'v2' with an optional weight
        if weight is not None:
            self.weighted = True
            new_node = GraphNode(v2, weight)
        else:
            new_node = GraphNode(v2)

        # Add the new node to the adjacency list of 'v1'
        new_node.next = self.adj_list[v1]
        self.adj_list[v1] = new_node

    def display(self):
        # Display the adjacency list of the graph
        for i in range(self.V):
            print(f"Vertex {i}:", end="")
            temp = self.adj_list[i]
            while temp:
                # Print the vertex and weight if the graph is weighted
                if self.weighted and temp.weight is not None:
                    print(f" -> ({temp.vertex}, {temp.weight})", end="")
                else:
                    print(f" -> {temp.vertex}", end="")
                temp = temp.next
            print()

برای نمایش لیست مجاورت یک گراف بدون وزن و جهت‌دار به‌صورت زیر عمل می‌کنیم:

# Create an unweighted graph
unweighted_graph = DirectedGraph(4)

# Add edges
unweighted_graph.add_edge(0, 1)
unweighted_graph.add_edge(1, 2)
unweighted_graph.add_edge(1, 3)
unweighted_graph.add_edge(2, 3)

# Display the Adjacency list
print("Adjacency list:")
unweighted_graph.display()

Adjacency list:
Vertex 0: -> 1
Vertex 1: -> 3 -> 2
Vertex 2: -> 3
Vertex 3:

برای نمایش لیست مجاورت یک گراف وزن‌دار و جهت‌دار به‌صورت زیر عمل می‌کنیم:

# Create a weighted graph
graph = DirectedGraph(4)

# Add edges
graph.add_edge(0, 1, 10)
graph.add_edge(1, 2, 30)
graph.add_edge(1, 3, 40)
graph.add_edge(2, 3, 60)

# Display the Adjacency list
print("Adjacency list:")
graph.display()

Adjacency list:
Vertex 0: -> (1, 10)
Vertex 1: -> (3, 40) -> (2, 30)
Vertex 2: -> (3, 60)
Vertex 3:

عملیات‌های مهم با لیست مجاورت

در این بخش، به بررسی برخی از عملیات‌های مهم و کاربردی که می‌توان با استفاده از لیست مجاورت انجام داد، می‌پردازیم. این عملیات‌ها شامل بررسی وجود یال بین دو راس و پیدا کردن همسایگان یک راس می‌باشند.

بررسی وجود یال بین دو راس

برای بررسی وجود یال بین دو راس مشخص، از لیست مجاورت استفاده می‌کنیم. در این روش، لیست مربوط به راس اول را پیمایش می‌کنیم تا ببینیم آیا راس دوم در این لیست وجود دارد یا خیر. این روش به دلیل استفاده از لیست پیوندی، در گراف‌های پراکنده بهینه‌تر است زیرا فقط رئوس متصل به راس مورد نظر بررسی می‌شوند.

نحوه بررسی وجود یال بین دو راس در پایتون

برای بررسی وجود یال بین دو راس، یک تابع به نام has_edge تعریف می‌کنیم. این تابع، لیست مجاورت گراف و دو راس v1 و v2 را به عنوان ورودی دریافت می‌کند. سپس به ابتدای لیست مجاورت راس v1 اشاره می‌کند و تا وقتی که به‌انتهای لیست نرسیده، هرگره را بررسی می‌کند. اگر راس موجود در گره فعلی برابر با v2 باشد، تابع True برمی‌گرداند. در غیر این صورت، به گره بعدی در لیست پیوندی می‌رود. اگر تا انتهای لیست هیچ گره‌ای با راس v2 یافت نشد، تابع False برمی‌گرداند:

def has_edge(adj_list, v1, v2):
    # Adjacency list of vertex v1
    current = adj_list[v1]
    # Traverse the adjacency list
    while current is not None:
        # Check if the current vertex is v2
        if current.vertex == v2:
            return True
        # Move to the next vertex in the adjacency list
        current = current.next
    return False

# Create a graph
graph = Graph(4)

# Add edges
graph.add_edge(0, 1)
graph.add_edge(1, 2)
graph.add_edge(1, 3)
graph.add_edge(2, 3)

# Display the Adjacency list
print("Adjacency list:")
graph.display()

# Check if there is an edge between vertices 1 and 2
if has_edge(graph.adj_list, 1, 2):
    print("There is an edge between vertices 1 and 2.")
else:
    print("There is no edge between vertices 1 and 2.")

Adjacency list:
Vertex 0: -> 1
Vertex 1: -> 3 -> 2 -> 0
Vertex 2: -> 3 -> 1
Vertex 3: -> 2 -> 1

پیدا کردن همسایگان یک راس

برای پیدا کردن همسایگان یک راس، از لیست مجاورت استفاده می‌کنیم. در این روش، تمامی گره‌های موجود در لیست مجاورت راس مورد نظر را پیمایش می‌کنیم و رئوس مجاور را به یک لیست نتایج اضافه می‌کنیم. این روش به ما اجازه می‌دهد تا تمام رئوس متصل به یک راس خاص را به راحتی پیدا کنیم.

نحوه پیدا کردن همسایگان یک راس در پایتون

برای برای پیدا کردن همسایگان یک راس مشخص، یک تابع به نام get_neighbors  تعریف می‌کنیم. این تابع، لیست مجاورت گراف و یک راس v را به عنوان ورودی دریافت می‌کند. سپس به ابتدای لیست مجاورت راس v اشاره می‌کند و تا وقتی که به‌انتهای لیست نرسیده، هرگره را بررسی می‌کند و راس موجود در گره فعلی را به لیست همسایگانش اضافه می‌کند. درنهایت، لیست همسایگان بازگردانده می‌شود:

def get_neighbors(adj_list, v):
    # An empty list to store neighbors
    neighbors = []
    # Adjacency list of vertex v
    current = adj_list[v]
    # Traverse the adjacency list
    while current is not None:
        # Add the current vertex to the neighbors list
        neighbors.append(current.vertex)
        # Move to the next vertex in the adjacency list
        current = current.next
    return neighbors

# Create a graph
graph = Graph(4)

# Add edges
graph.add_edge(0, 1)
graph.add_edge(1, 2)
graph.add_edge(1, 3)
graph.add_edge(2, 3)

# Display the Adjacency list
print("Adjacency list:")
graph.display()

# Get the neighbors of vertex 1
neighbors = get_neighbors(graph.adj_list, 1)
print("Neighbors of vertex 1:", neighbors)

Adjacency list:
Vertex 0: -> 1
Vertex 1: -> 3 -> 2 -> 0
Vertex 2: -> 3 -> 1
Vertex 3: -> 2 -> 1

Neighbors of vertex 1: [3, 2, 0]

بررسی پیچیدگی زمانی و مکانی لیست مجاورت

• پیچیدگی مکانی: فضای ذخیره‌سازی لیست مجاورت به صورت O(n + e) است، زیرا فقط رئوس (n) و یال‌های (e) موجود در گراف در لیست ذخیره می‌شوند.
• پیچیدگی زمانی: محاسبه عملیات‌های مختلف بر روی لیست مجاورت معمولاً به زمان O(n + e) نیاز دارد، زیرا برای هر عملیات ممکن است نیاز باشد تمامی رئوس و یال‌های گراف بررسی شوند.

کاربردهای لیست مجاورت

لیست مجاورت در دنیای واقعی نیز کاربردهایی دارد که درادامه آن‌ها را بررسی می‌کنیم:

موتورهای جستجو

موتورهای جستجو از گراف‌ها برای نمایش ارتباط بین صفحات وب استفاده می‌کنند و برای نمایش این گراف‌ها، از لیست مجاورت استفاده می‌شود. در این لیست هر صفحه به عنوان یک راس و لینک‌های بین صفحات به عنوان یال‌ها در نظر گرفته می‌شوند. لیست مجاورت به بهینه‌سازی فرآیند پیمایش و رتبه‌بندی صفحات کمک می‌کند.

سیستم‌های توصیه‌گر

سیستم‌های توصیه‌گر (مثل توصیه فیلم‌ها، محصولات و غیره) از گراف‌ها برای مدل‌سازی ارتباطات بین کاربران و آیتم‌ها استفاده می‌کنند. لیست مجاورت به دلیل کارایی در پیمایش و یافتن همسایگان نزدیک برای توصیه‌ها مورد استفاده قرار می‌گیرد.

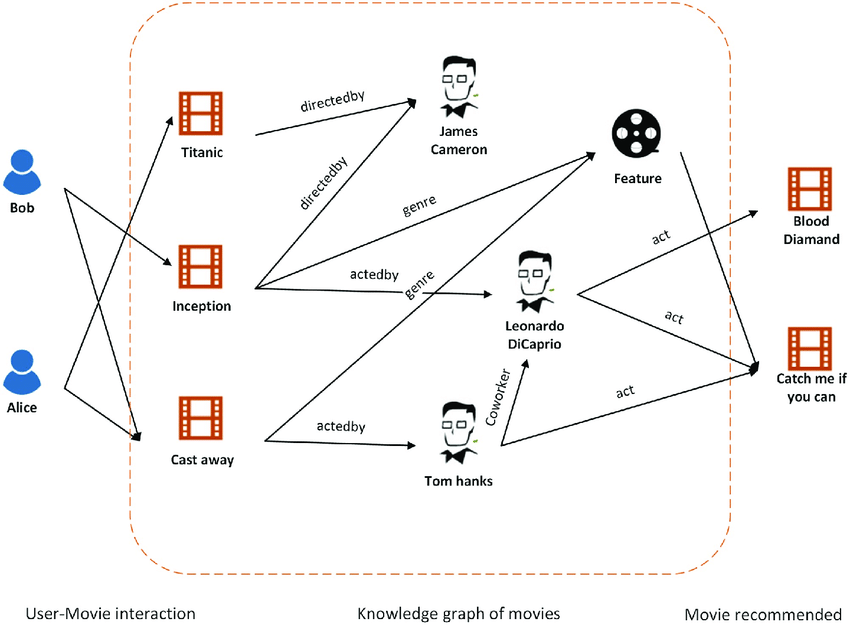
تحلیل شبکه‌های بیولوژیکی

در بیولوژی و پزشکی، شبکه‌های مختلفی مثل شبکه‌های پروتئین-پروتئین، شبکه‌های ژنی و شبکه‌های عصبی وجود دارند که به‌صورت گراف نمایش داده می‌شوند. لیست مجاورت به تحلیل ارتباطات و تعاملات بین اجزای مختلف این شبکه‌ها کمک می‌کند.

مدل‌سازی بازی‌ها

در طراحی و پیاده‌سازی بازی‌های کامپیوتری، گراف‌ها برای مدل‌سازی محیط بازی، مسیرها و ارتباطات بین نقاط مختلف استفاده می‌شوند. نمایش این گراف‌ها به‌صورت لیست مجاورت به مدیریت و پیمایش آن‌ها کمک می‌کند.

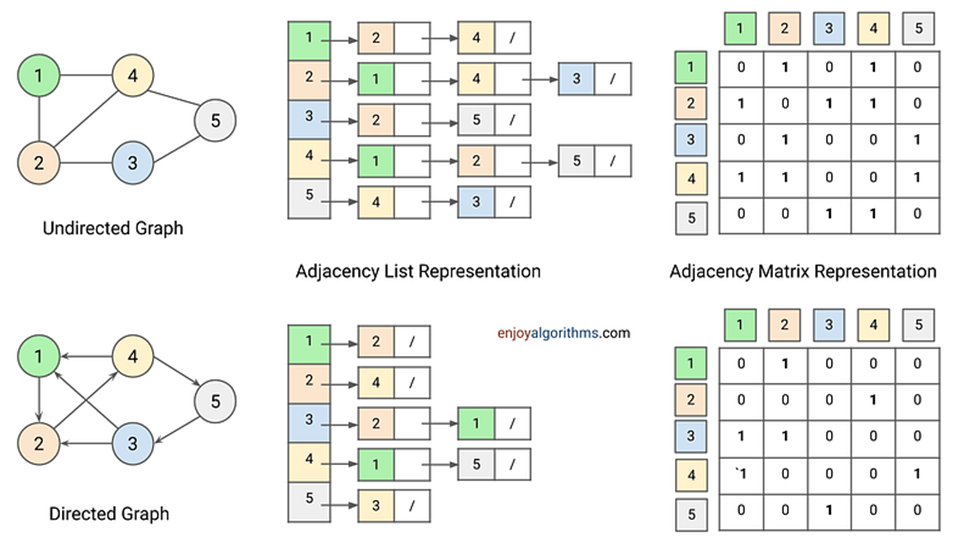
مقایسه ماتریس مجاورت و لیست مجاورت

ماتریس مجاورت و لیست مجاورت دو روش متداول برای نمایش گراف‌ها هستند. هر یک از این روش‌ها دارای مزایا و معایب خاص خود می‌باشند که درادامه به مقایسه آن‌ها پرداخته‌ایم:

ماتریس مجاورت

همان‌طور که در ابتدای این مقاله توضیح دادیم، ماتریس مجاورت یک ماتریس مربعی است که در آن سطرها و ستون‌ها نمایانگر رئوس گراف هستند. در این ماتریس، اگر بین دو راس یک یال وجود داشته باشد، مقدار مربوط به آن خانه برابر ۱ (یا وزن یال) و در غیر این صورت برابر ۰ است.

مزایا

• زمان دسترسی سریع: با ماتریس مجاورت تشخیص به وجود یا عدم وجود یک یال بین دو راس در زمان ثابت (O(1)) امکان‌پذیر است.
• سادگی پیاده‌سازی: پیاده‌سازی ماتریس مجاورت نسبتاً ساده و سرراست است.

معایب

• مصرف حافظه زیاد: مصرف حافظه برابر با O(n²) است، که n تعداد رئوس گراف می‌باشد. این موضوع برای گراف‌های بزرگ مشکل‌ساز است، به‌ویژه اگر گراف دارای یال‌های کمی باشد.
• سختی در پیمایش یال‌ها: پیمایش تمامی یال‌های یک راس خاص نیازمند پیمایش یک سطر کامل ماتریس است که زمان O(n) را می‌طلبد.

لیست مجاورت

لیست مجاورت از یک مجموعه لیست‌های پیوندی یا آرایه‌ای تشکیل شده که هر لیست یا آرایه نمایانگر رئوس مجاور یک راس خاص است. هر گره در لیست مجاورها شامل یک راس مجاور و وزن یال (در صورت وزن‌دار بودن گراف) می‌باشد.

مزایا

• مصرف حافظه بهینه: مصرف حافظه برابر با O(n + e) است، که n تعداد رئوس و e تعداد یال‌های گراف می‌باشد. این موضوع باعث می‌شود لیست مجاورت برای گراف‌های بزرگ و پراکنده مناسب‌تر باشد.
• پیمایش آسان یال‌ها: پیمایش تمامی یال‌های یک راس خاص با پیمایش لیست مجاورت آن راس امکان‌پذیر است که زمان O(e) را برای هر راس می‌طلبد.

معایب

• دسترسی کندتر: دسترسی به وجود یا عدم وجود یک یال بین دو راس ممکن است در بدترین حالت به زمان O(n)  نیاز داشته باشد.
• پیاده‌سازی پیچیده‌تر: پیاده‌سازی لیست مجاورت نسبت به ماتریس مجاورت پیچیده‌تر است و نیاز به مدیریت حافظه پویا دارد.

در جدول زیر می‌توانید نکاتی که در بالا بررسی شد را ببینید:

ویژگی	ماتریس مجاورت	لیست مجاورت
مصرف حافظه	O(n2)	O(n + e)
دسترسی به یال‌ها	O(1)	O(e)
افزودن یال	O(1)	O(1)
حذف یال	O(1)	O(e)
مناسب برای گراف‌های	گراف‌های متراکم (Dense)	گراف‌های پراکنده (Sparse)
پیاده‌سازی	ساده‌تر	پیچیده‌تر

نمایش هندسی

یکی دیگر از روش‌های نمایش گراف، نمایش هندسی یا ترسیم گراف به صورت تصویری است که در آن رئوس به صورت نقاط و یال‌ها به صورت خطوط نشان داده می‌شوند. این روش برای فهم بصری گراف‌ها بسیار مفید است. نمایش هندسی به ما امکان می‌دهد تا الگوها و ارتباطات را به صورت بصری مشاهده کنیم و به تحلیل‌های پیچیده‌تری بپردازیم. این نوع نمایش در زمینه‌های مختلفی از جمله طراحی شبکه‌های الکترونیکی و معماری سیستم‌های نرم‌افزاری کاربرد دارد.

یکی از روش‌های نمایش هندسی گراف‌ها، استفاده از کتابخانه‌های زبان‌های برنامه‌نویسی است. در این بخش نحوه کار با یکی تا از کتابخانه‌های معروف پایتون یعنی برای کار با گراف‌ها را با یکدیگر مرور می‌کنیم. کتابخانه مورد نظر ما NetworkX است.

NetworkX یک کتابخانه قدرتمند پایتون برای ایجاد و مطالعه ساختارها، دینامیک و کارکردهای شبکه‌های پیچیده است. این کتابخانه امکانات متعددی برای مدل‌سازی و تحلیل گراف‌ها فراهم می‌کند و باکمک آن می‌توان به‌راحتی الگوریتم‌های پیچیده را پیاده‌سازی کرد.

نصب کتابخانه NetworkX

برای کار با این کتابخانه، ابتدا باید آن  را نصب کنیم. برای نصب آن از دستور زیر استفاده می‌کنیم:

!pip install networkx

وارد کردن کتابخانه‌ها

حال باید NetworkX و numpy را که کتابخانه‌های مورد نیاز ما برای کار با گراف هستند، وارد ‌کنیم:

import networkx as nx
import numpy as np

ایجاد یک گراف بدون جهت و رسم آن

برای ایجاد یک گراف بدون جهت از دستور nx.Graph استفاده می‌کنیم. سپس مطابق کد زیر یال‌های گراف را اضافه می‌کنیم:

# Create an undirected graph
G = nx.Graph()

# Add edges to the graph
G.add_edge('A', 'B')
G.add_edge('B', 'C')
G.add_edge('B', 'D')
G.add_edge('C', 'A')

برای رسم این گراف می‌توانیم از nx.draw استفاده کنیم:

# Draw the graph
nx.draw(G, with_labels=True, node_color='skyblue', node_size=700, edge_color='black')

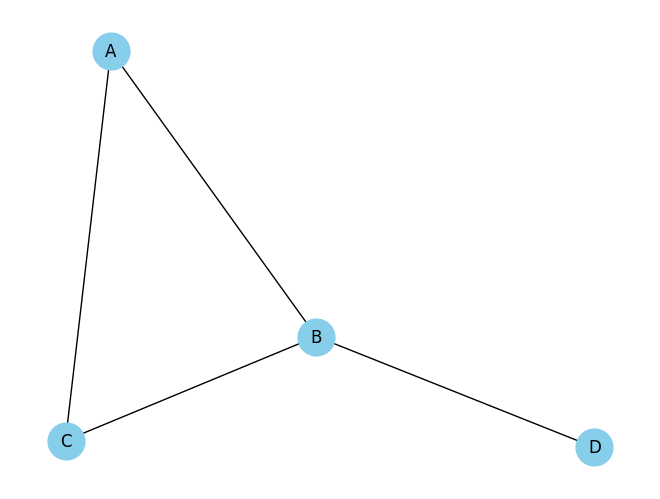
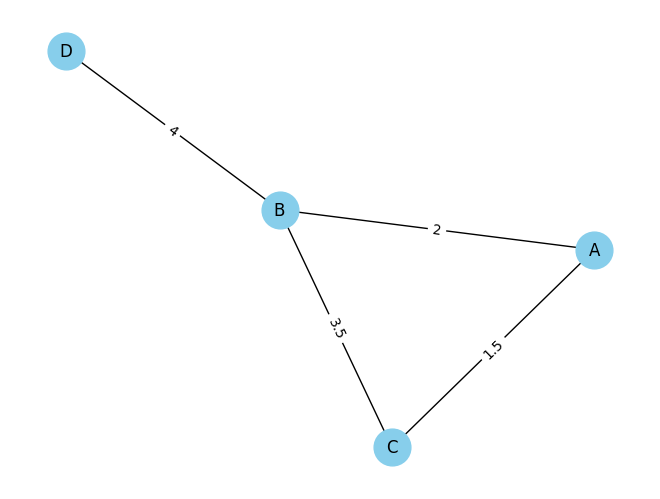
همچنین می‌توان با مقداردهی به متغیر weight در هنگام ساخت گراف، برای هر یال وزنی مشخص کنیم:

# Create an undirected graph
G = nx.Graph()

# Add edges to the graph
G.add_edge('A', 'B', weight=2)
G.add_edge('B', 'C', weight=3.5)
G.add_edge('B', 'D', weight=4)
G.add_edge('C', 'A', weight=1.5)

برای رسم گراف‌های وزن‌دار نیز باید از کد زیر استفاده کرد:

# Draw Graph
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_color='skyblue', node_size=700, edge_color='black')
edge_labels = nx.get_edge_attributes(G, 'weight')
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels)

ایجاد گراف جهت‌دار

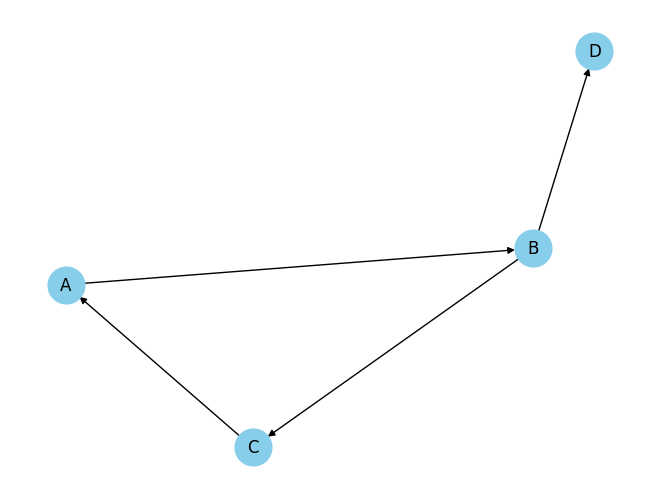
برای ایجاد یک گراف جهت‌دار از nx.DiGraph استفاده می‌کنیم و مطابق آنچه در بخش‌های قبل آموختیم، گراف را رسم می‌کنیم. توجه کنید که برای مشاهده جهت یال‌ها لازم است در هنگام ترسیم آن، متغیر arrows را True کنیم:

# Create a directed graph
G = nx.DiGraph()

# Add edges to the graph
G.add_edge('A', 'B')
G.add_edge('B', 'C')
G.add_edge('B', 'D')
G.add_edge('C', 'A')

# Draw the graph
nx.draw(G, with_labels=True, arrows=True, node_color='skyblue', node_size=700, edge_color='black')

ایجاد ماتریس مجاورت

این کتابخانه همچنین قابلیت تشکیل ماتریس مجاورت گراف‌ها را نیز دارد:

# Create a graph
G = nx.Graph()

# Add edges to the graph
G.add_edge(1, 2)
G.add_edge(2, 3)
G.add_edge(3, 1)

# Generate the adjacency matrix
A = nx.adjacency_matrix(G).todense()

print("Adjacency Matrix")
print(A)

Adjacency Matrix
[[0 1 1]
[1 0 1]
[1 1 0]]

برای گراف وزن‌دار نیز به‌صورت زیر عمل می‌کنیم:

# Create a graph
G = nx.Graph()

# Add edges to the graph with weights
G.add_edge(1, 2, weight=3)
G.add_edge(2, 3, weight=5)
G.add_edge(3, 1, weight=7)

# Generate the adjacency matrix
A = nx.adjacency_matrix(G).todense()

print("Adjacency Matrix")
print(A)

Adjacency Matrix
[[0 3 7]
[3 0 5]
[7 5 0]]

ایجاد ماتریس درجه

با دستور زیر می‌توانید به‌راحتی ماتریس درجه یک گراف را بسازید:

# Create a graph
G = nx.Graph()

# Add edges to the graph with weights
G.add_edge(1, 2, weight=3)
G.add_edge(2, 3, weight=5)
G.add_edge(3, 1, weight=7)

# Calculate the degree of each node with weights
degree_dict = dict(G.degree(weight='weight'))

# Get the nodes of the graph
nodes = G.nodes()

# Initialize a degree matrix with zeros
degree_matrix = np.zeros((len(nodes), len(nodes)))

# Fill the degree matrix with the degrees of the nodes
for i, node in enumerate(nodes):
    degree_matrix[i, i] = degree_dict[node]

print("Degree Matrix")
print(degree_matrix)

Degree Matrix
[[10. 0. 0.]
[ 0. 8. 0.]
[ 0. 0. 12.]]

ایجاد ماتریس رخداد

برای تشکیل ماتریس رخداد که نشان‌دهنده ارتباط یال‌ها و گره‌ها است، از دستور زیر استفاده می‌کنیم:

# Create a graph
G = nx.Graph()

# Add edges to the graph
G.add_edge(1, 2)
G.add_edge(2, 3)
G.add_edge(3, 1)

# Generate the incidence matrix
incidence_matrix = nx.incidence_matrix(G, oriented=False).todense()

print("Incidence Matrix:")
print(incidence_matrix)

Incidence Matrix:
[[1. 1. 0.]
[1. 0. 1.]
[0. 1. 1.]]

ایجاد لیست مجاورت

لیست مجاورت شیوه دیگری از نمایش گراف در کامپیوتر است که ارتباط گره‌ها را نشان می‌دهد. با کد زیر به‌راحتی می‌توان باکمک این کتابخانه لیست مجاورت ماتریس مورد نظر را ایجاد کرد:

# Create a graph
G = nx.Graph()

# Add edges to the graph
G.add_edge(1, 2)
G.add_edge(2, 3)
G.add_edge(3, 1)

# Convert the graph to an adjacency list
adj_list = nx.to_dict_of_lists(G)

print(adj_list)

{1: [2, 3], 2: [1, 3], 3: [2, 1]}

مجموعه کامل کدهای استفاده شده در این مطلب، از گیت‌هاب ریپوزیتوری Graph Representations قابل دسترسی است.

مزایا و معایب هر نوع نمایش

هر یک از روش‌های نمایش گراف دارای مزایا و معایب خاص خود هستند که باید باتوجه به نوع مسئله و ویژگی‌های گراف انتخاب شوند. درادامه مزایا و معایب هر روش را بررسی می‌کنیم:

مزایای نمایش ماتریسی

• امکان انجام عملیات ریاضی پیچیده: نمایش ماتریسی امکان انجام عملیات ریاضی پیچیده بر روی گراف را فراهم می‌کند و برای گراف‌های متراکم که تعداد زیادی یال دارند، کارایی بالایی دارد.
• دسترسی سریع به اطلاعات ارتباطات: در این روش، دسترسی به اطلاعات مربوط به ارتباطات بین رئوس بسیار سریع است که به اجرای سریع الگوریتم‌ها کمک می‌کند.
• پیاده‌سازی الگوریتم‌های پیچیده: این نوع نمایش به ما کمک می‌کند تا الگوریتم‌های پیچیده‌تری را به راحتی پیاده‌سازی کنیم و تحلیل‌های دقیق‌تری انجام دهیم.

معایب نمایش ماتریسی

• نیاز به فضای ذخیره‌سازی زیاد: این نوع نمایش به فضای ذخیره‌سازی زیادی نیاز دارد و برای گراف‌های پراکنده که تعداد یال‌های کمی نسبت به تعداد رئوس دارند، مناسب نیست.
• پیچیدگی در تغییرات گراف: تغییرات در گراف (مانند اضافه یا حذف کردن یال‌ها) ممکن است پیچیده‌تر باشد و مدیریت و پردازش ماتریس‌ها در گراف‌های بزرگ می‌تواند دشوار باشد.
• حجم داده‌های بالا: در گراف‌های بزرگ با تعداد زیادی راس و یال، حجم داده‌های ماتریس می‌تواند بسیار زیاد شود که مدیریت و پردازش آن‌ها را دشوار می‌سازد.

مزایای نمایش لیستی

• فضای ذخیره‌سازی کمتر: نمایش لیستی فضای کمتری را اشغال می‌کند و برای گراف‌های پراکنده بسیار مناسب است.
• دسترسی سریع به همسایگان راس خاص: این روش به ما امکان می‌دهد تا به سرعت به همسایگان یک راس خاص دسترسی پیدا کنیم و تغییرات در گراف را به سادگی اعمال کنیم.
• مناسب برای گراف‌های داینامیک: این نوع نمایش به خصوص در گراف‌های داینامیک که تغییرات زیادی دارند، بسیار مفید است.

معایب نمایش لیستی

• دشواری در انجام عملیات ریاضی پیچیده: عملیات ریاضی پیچیده بر روی نمایش لیستی دشوارتر است و برای گراف‌های متراکم که تعداد زیادی یال دارند، کارایی کمتری دارد.
• دسترسی زمان‌بر به اطلاعات ارتباطات: دسترسی به اطلاعات مربوط به ارتباطات بین همه رئوس در این روش ممکن است زمان‌بر باشد و برای الگوریتم‌های تحلیل شبکه که نیاز به بررسی تمامی یال‌ها دارند، این نوع نمایش ممکن است کندتر عمل کند.

مزایای نمایش هندسی

• درک بصری و شهودی: نمایش هندسی گراف‌ها به کاربران اجازه می‌دهد تا ساختار گراف را به صورت بصری مشاهده کنند. این نوع نمایش به ویژه برای فهم روابط پیچیده و الگوهای پنهان در داده‌ها مفید است.
• شناسایی الگوها و خوشه‌ها: با استفاده از نمایش هندسی، شناسایی الگوها و خوشه‌های مختلف در گراف آسان‌تر می‌شود. این امر به تحلیلگران کمک می‌کند تا دسته‌بندی‌های طبیعی در داده‌ها را بیابند و آن‌ها را تحلیل کنند.
• شناسایی نقاط کلیدی: نمایش هندسی به شناسایی نقاط کلیدی مانند رئوس مرکزی، مسیرهای مهم و یال‌های بحرانی کمک می‌کند. این اطلاعات برای بهینه‌سازی شبکه‌ها و بهبود عملکرد آن‌ها حیاتی هستند.
• مناسب برای ارائه‌ها: نمایش هندسی به دلیل ویژگی‌های بصری و شفافیت، برای ارائه‌ها و توضیح مفاهیم به مخاطبان غیر تخصصی مناسب است. این نوع نمایش به افراد کمک می‌کند تا بدون نیاز به دانش تخصصی، ساختار و ارتباطات موجود در گراف را درک کنند.

معایب نمایش هندسی

• پیچیدگی در رسم گراف‌های بزرگ: نمایش هندسی گراف‌های بزرگ و پیچیده ممکن است باعث بروز مشکلاتی نظیر همپوشانی رئوس و یال‌ها شود. این امر می‌تواند منجر به کاهش خوانایی و دشواری در تفسیر گراف شود.
• نیاز به الگوریتم‌های پیچیده: رسم گراف‌های بزرگ به صورت هندسی نیاز به الگوریتم‌های پیچیده برای یافتن چیدمان مناسب دارد. این الگوریتم‌ها ممکن است نیازمند محاسبات زیاد و زمان‌بر باشند.
• محدودیت در دقت: در برخی موارد، نمایش هندسی نمی‌تواند به دقت تمام ویژگی‌ها و جزئیات گراف را نمایش دهد. این مشکل به خصوص در گراف‌هایی با تعداد زیاد یال‌ها و رئوس بروز می‌کند.
• محدودیت‌های فضایی: نمایش هندسی ممکن است نیاز به فضای نمایش زیادی داشته باشد و این محدودیت باعث شود که نتوان تمامی جزئیات را به خوبی مشاهده کرد. این امر به خصوص در نمایش گراف‌های سه‌بعدی یا گراف‌هایی با چگالی بالا مشکل‌ساز است.

ابزارها و نرم‌افزارهای مرتبط با نمایش گراف

امروزه ابزارها و نرم‌افزارهای متعددی برای نمایش و تحلیل گراف‌ها وجود دارد که به پژوهشگران و دانشمندان در کارهای خود کمک می‌کنند.

برخی از نرم‌افزارهای محبوب برای رسم گراف‌ها عبارتند از:

Gephi

Gephi یک نرم‌افزار متن‌باز برای تحلیل و مصورسازی شبکه‌های پیچیده است. این نرم‌افزار امکانات متعددی برای ترسیم و تحلیل گراف‌ها فراهم می‌کند و به ما امکان می‌دهد تا به راحتی داده‌های پیچیده را به صورت بصری مشاهده و تحلیل کنیم.

Cytoscape

Cytoscape یک نرم‌افزار متن‌باز برای مصورسازی شبکه‌های مولکولی و تعاملات بیولوژیکی است. این نرم‌افزار به خصوص در بیوانفورماتیک و تحلیل شبکه‌های ژنتیکی کاربرد دارد و ابزارهای قدرتمندی برای مدل‌سازی و تحلیل داده‌های بیولوژیکی فراهم می‌کند.

Graphviz

Graphviz یک ابزار برای رسم گراف‌ها و نمودارهای شبکه‌ای است که از زبان DOT برای توصیف گراف‌ها استفاده می‌کند. این ابزار امکانات متعددی برای ترسیم و تحلیل گراف‌ها فراهم می‌کند و به ما امکان می‌دهد تا به راحتی گراف‌های پیچیده را مدل‌سازی و تحلیل کنیم.

جمع‌بندی

گراف‌ها به عنوان ابزاری مؤثر برای مدل‌سازی و تحلیل روابط پیچیده در زمینه‌های مختلف از جمله علوم رایانه، شبکه‌های اجتماعی و بیوانفورماتیک مطرح هستند. در این مقاله به تفصیل درباره انواع نمایش‌های مختلف گراف از جمله ماتریس مجاورت، ماتریس درجه، ماتریس رخداد و لیست مجاورت پرداختیم. هر یک از این روش‌ها دارای مزایا و معایب خاص خود هستند و انتخاب صحیح آن‌ها بستگی به نوع مسئله و ویژگی‌های گراف دارد.

با فهم عمیق‌تر از هر یک از این روش‌ها، می‌توانیم گراف‌ها را به طور موثرتری تحلیل و بررسی کنیم. همچنین، استفاده از ابزارها و نرم‌افزارهای مناسب می‌تواند فرآیند تحلیل گراف‌ها را ساده‌تر و کارآمدتر کند. در نهایت، درک دقیق‌تر و کامل‌تر از گراف‌ها و نحوه نمایش آن‌ها می‌تواند به ما در حل مسائل پیچیده‌تر و انجام تحلیل‌های دقیق‌تر کمک کند.

سوالات متداول

نظریه گراف چیست؟

نظریه گراف شاخه‌ای از ریاضیات است که به مطالعه گراف‌ها و ارتباطات بین رئوس و یال‌های آن‌ها می‌پردازد. این نظریه به ما امکان می‌دهد تا روابط پیچیده را به صورت گرافیکی نمایش دهیم و به تحلیل و بررسی دقیق‌تر آن‌ها بپردازیم.

ماتریس مجاورت چیست؟

ماتریس مجاورت یک روش نمایش گراف است که در آن از یک ماتریس مربعی برای نشان دادن وجود یا عدم وجود یال بین رئوس استفاده می‌شود. اگر یک یال بین دو راس وجود داشته باشد، مقدار عنصر مربوطه یک و در غیر این صورت صفر است.

نمایش لیستی چه مزایایی دارد؟

نمایش لیستی فضای کمتری را اشغال می‌کند و برای گراف‌های پراکنده بسیار مناسب است. این روش به ما امکان می‌دهد تا به سرعت به همسایگان یک راس خاص دسترسی پیدا کنیم و تغییرات در گراف را به سادگی اعمال کنیم.

نمایش هندسی گراف چیست؟

نمایش هندسی شامل ترسیم گراف به صورت تصویری است که در آن رئوس به صورت نقاط و یال‌ها به صورت خطوط نشان داده می‌شوند. این روش برای فهم بصری گراف‌ها بسیار مفید است و به ما امکان می‌دهد تا الگوها و ارتباطات را به صورت بصری مشاهده کنیم.

چه عواملی در انتخاب نوع نمایش گراف مؤثرند؟

نوع مسئله، ویژگی‌های گراف و نیاز به تحلیل‌های خاص از جمله عواملی هستند که در انتخاب نوع نمایش گراف تأثیرگذارند. برای مثال، برای گراف‌های متراکم نمایش ماتریسی و برای گراف‌های پراکنده نمایش لیستی مناسب‌تر است.

یادگیری تحلیل داده را از امروز شروع کنید!

دنیای داده‌ها جذاب است و دانستن علم داده، توانایی تحلیل داده‌، یا بازاریابی مبتنی بر داده، شما را برای فرصت‌های شغلی بسیاری مناسب می‌کند. فارغ از رشته‌ و پیش‌زمینه‌، می‌توانید حالا شروع کنید و از سطح مقدماتی تا پیشرفته بیاموزید. اگر دوست دارید به این حوزه وارد شوید، پیشنهاد می‌کنیم با کلیک روی این لینک قدم اول را همین حالا بردارید.

مشاوران کافه‌تدریس به شما کمک می‌کنند مسیر یادگیری برای ورود به این حوزه را شروع کنید:

دوره جامع دیتا ساینس و ماشین لرنینگ