موفقیت در درس ریاضی عمومی به تمرین و تکرار زیاد نیاز دارد. درصد بالای داوطلبان در این درس و ضریب آن باعث اهمیت بالای آن میشود. برای پیشبردن طرز اصولی درست مطالعه این درس شما حتماً نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید. کاربردهای مشتق از مباحث پرسؤال ریاضی کنکور ارشد است که با آن آشنا خواهیم شد.
مشتق به زبان ساده
حد نسبت تغییرات تابع به متغیر زمانی را که بسیار کوچک شود بهمیزانی که به صفر میل کند مشتق تابع گوییم. مشتق از مباحث مهم ریاضیات است. مشتق را با یا نشان میدهیم. درواقع این عملیات همان شیب خط مماس در نقطه مدنظر است.
کاربرد مشتق
مشتق در زندگی کاربردهای مختلفی دارد. در ادامه برخی از این کاربردها را بررسی میکنیم.
شیب خط مماس
پیش از این گفتیم که مشتق در هندسه شیب خط مماس بر منحنی است. پس اولین کاربرد مشتق، بهدستآوردن شیب خط مماس بر منحنی است. از آنجا که خط قائم بر منحنی بر خط مماس نیز قائم است، پس به کمک مشتق میتوان شیب خط قائم را نیز پیدا کرد. با کمک این کاربرد مشتق و داشتن یک نقطه از منحنی میتوانیم معادله خط مماس و قائم را نیز به دست آوریم.
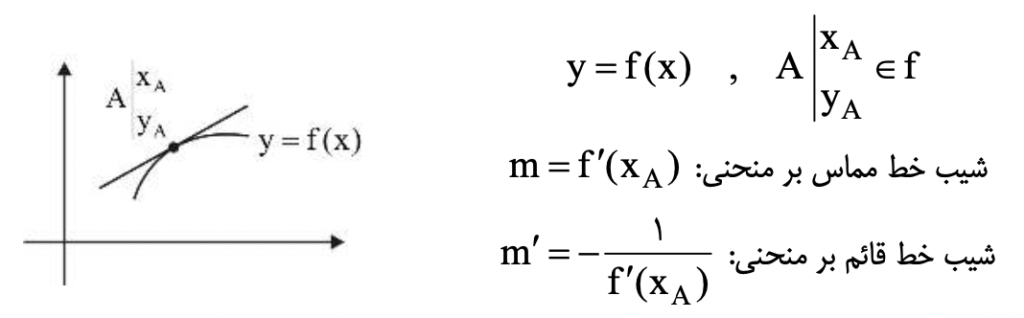
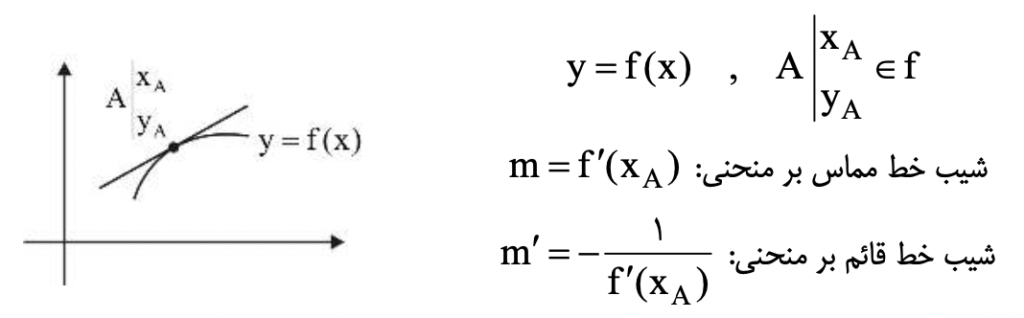
تعیین زاویه حاده میان دو منحنی
به زاویههای کمتر از ۹۰ درجه زاویه حاده میگویند. یکی از کاربردهای مشتق، بهدستآوردن زاویه حاده میان دو منحنی است. به زاویه میان دو خط مماس بر منحنی در نقطه تلاقی دو منحنی زاویه بین دو منحنی میگویند. برای بهدستآوردن زاویه
گام ۱. دو تابع را برابر هم قرار میدهیم تا نقطه تلاقی به دست آید؛
گام ۲. مشتق دو تابع را در نقطه تلاقی محاسبه میکنیم؛
گام ۳. با فرمول زیر زاویه را به دست میآوریم.
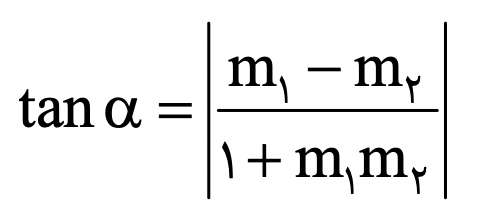
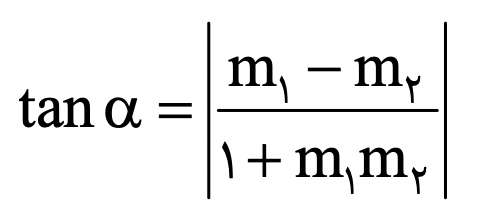
نقاط بحرانی
نقاطی که متعلق به دامنه تابع باشند که مشتق تابع در این نقاط برابر صفر باشد یا موجود نباشد نقاط بحرانی گویند. این نقاط ممکن است نقاط انفصال، اکسترممهای مطلق و نسبی یا نقاط دارای نیم مشتق چپ و راست باشد.
اکسترممهای نسبی میتوانند مینیمم یا ماکزیمم باشند. نقاطی که در آن نقطه نسبت به ارتفاع نثاط اطراف خود بیشتر یا برابر باشد، ماکزیمم و نقاطی را که کمتر یا برابر باشد مینیمم گویند. بهدستآوردن نقاط اکسترمم نیز از دیگر کاربردهای مشتق است.
آهنگ تغییرات
در توابع پارامتری، اگر متغیرهای وابسته را یک کمیت فیزیکی و پارامتر را زمان در نظر بگیریم، میتوان آهنگ تغییرات کمیتها برحسب زمان را برحسب هم بین نمود. مثلاً در محاسبهٔ سرعت متوسط یک جسم، مقدار تغییر مکان را تقسیم بر زمانی می کنیم که آن جسم طی کرده است. آهنگ تغییر، اندازهٔ این نسبتها را برای ما محاسبه میکند. اگر نسبت تغییرات را به طول یک بازهٔ زمانی بسنجیم، آهنگ متوسط تغییر را محاسبه کردهایم که این تعریف مشتق و یک کاربرد مشتق خواهد بود. اگر بازه زمانی بسیار کوچک شود و حد فرمول را محاسبه کنیم، آهنگ تغییر لحظهای بدست می آید.
اکسترمم مطلق
اکسترمم مطلق تابع در نقاط بحرانی اتفاق میافتد. بر این اساس کافی است برای یافتن اکسترممهای مطلق یک تابع، نقاط بحرانی تابع را به دست آورد و در تابع جایگذاری کرد. بیشترین عرض، ماکزیمم مطلق و کمترین عرض، مینیمم مطلق خواهد بود.
برای بهینهکردن یک تابع هدف کافی است عرض های اکسترممهای تابع را بیابیم. بر این اساس اگر تابع تکمتغیره بود، مشتق آن را نسبت به تنها متغیرش میگیریم و برابر صفر قرار میدهیم، ولی اگر تابع وابسته به بیش از یک متغیر بود از طریق یک جایگزینی تابع را تنها برحسب یک متغیر نمود سپس تابع جدید را بهینه میکنیم.
ریشهیابی
یکی دیگر از کاربردهای مشتق، اگر مشتق تابع n ریشه داشته باشد، خود تابع حداکثر n+1 ریشه دارد.
برای تعیین ریشه با قضیه مقدار میانگین دستکم تعداد ریشههای تایع را به دست میآوریم. براساس این قضیه اگر تابع در بازهای پیوسته باشد و f(a)*f(b)<0 باشد، در آن صورت معادله f(x)=0 حداقل یک ریشه در بازه مدنظر دارد.
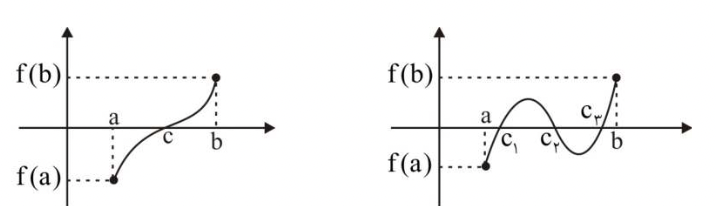

در مرحله بعد ریشههای مشتق را تعیین میکنیم و حداکثر تعداد ریشههای تابع را بدست میآوریم.
درنهایت با مقایسه تعداد ریشهها در دو گام قبل تعداد ریشهها را تعیین میکنیم.
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:
کلاس آنلاین ریاضی عمومی ۱ و ۲ رضا شکرزاد

