انواع روشهای انتگرال گیری یکی از مواردی است که برای موفقیت در درس ریاضی عمومی به تسلط بر آن نیاز دارید. از آنجا که اهمیت درس ریاضی عمومی در کنکور کارشناسی ارشد مدیریت کسبوکار، فنی و مهندسی و همچنین عمران زیاد است، شما نیاز دارید تا دستبهقلم شوید و سؤالات زیادی حل کنید. انواع روشهای انتگرال گیری را در ادامه معرفی کردهام تا با آنها بتوانید به سؤالات انتگرال پاسخ دهید.
اهمیت درس ریاضی عمومی ۱ و ۲
ریاضی عمومی ۱ و ۲ درس پایهای رشتههای مختلف است. اهمیت این درس زیاد است؛ اولین دلیل این است که این درس جزو سرفصلهای امتحانی رشتههای مختلف است. محتوای این درس بهقدری مهم است که آشنایی با مفهومهای آن به درک مفاهیم دیگر درسهای دورهی کارشناسی بسیار کمک میکند. دلیل دیگر اهمیت این درس و کلاس آنلاین ریاضی عمومی ۱ و ۲ نوع نگاه انتقادی در حل مسائل است.
طرز اصولی مطالعه ریاضی عمومی ۱ و ۲ چگونه است؟
در وبلاگ کافهتدریس برخی از موضوعهای مهم دروس را بهصورت ساده به شما آموزش خواهیم داد تا با مباحث این رشته آشنا شوید. این مقاله به انواع روشهای انتگرال گیری میپردازد.
انتگرال
در ریاضیات انتگرال روشی برای اختصاص اعداد به توابع است، بهگونهای که جابهجایی مساحت، حجم و دیگر مفاهیم برآمده از ترکیب دادههای بینهایت کوچک را به وسیله آن بتوان توصیف کرد. انتگرالگیری یکی از دو عمل مهم در حساب دیفرانسیل و انتگرال است. عمل معکوس آن مشتقگیری است.
روشهای انتگرالگیری
بسیاری از توابع از چند تابع مختلف تشکیل شدهاند. در برخی از توابع هم با اینکه همجنس هستند، نمیتوان بهسادگی انتگرالشان را به دست آورد. برای انتگرالگیری از این توابع باید از روشهایی برای محاسبه آنها استفاده کنیم.
فرمولهای انتگرال گیری
برای توابعی که از یک جنس و ساده هستند میتوانیم از فرمولهای انتگرال گیری استفاده کنیم. این فرمولها و قواعد با عکس عمل مشتق به دست میآیند:


روش انتگرال گیری تغییر متغیر
در برخی از توابع برای محاسبه راحتتر میتوانیم عبارتی از متغیرها را بهعنوان متغیر جدید فرض کنیم. این فرض زمانی انجام میشود که مشتق عبارت در کنار آن قرار گرفته باشد؛ برای مثال تابع به صورت مشتق زیر رادیکال بدون ضریب ۳ در پشت آن قرار دارد. با ضرب و تقسیم در عدد ۳ میتوان زیر انتگرال را بهعنوان عبارت متفیر و عبارت پشت رادیکال را بهعنوان مشتق آن محاسبه کنیم. برای حل این انتگرال بهصورت زیر با روش تغییر متغیر عمل میکنیم:
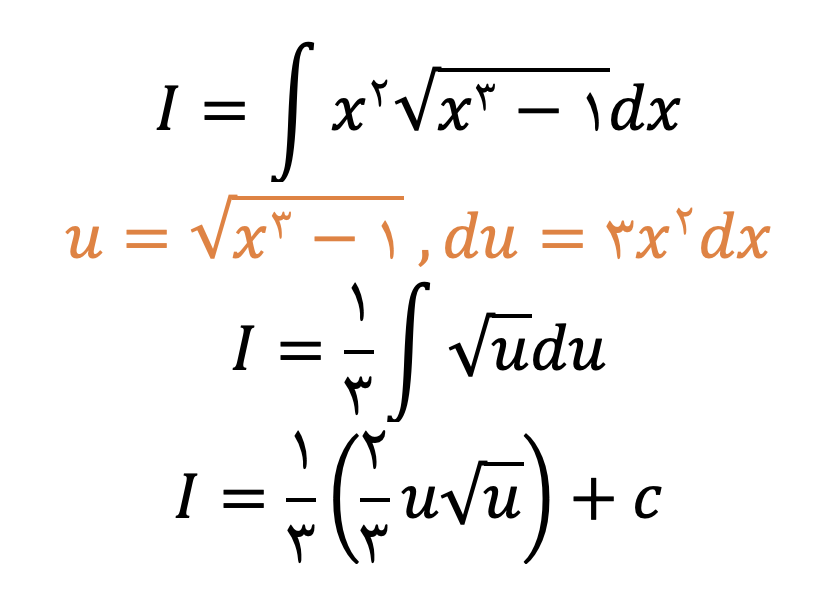
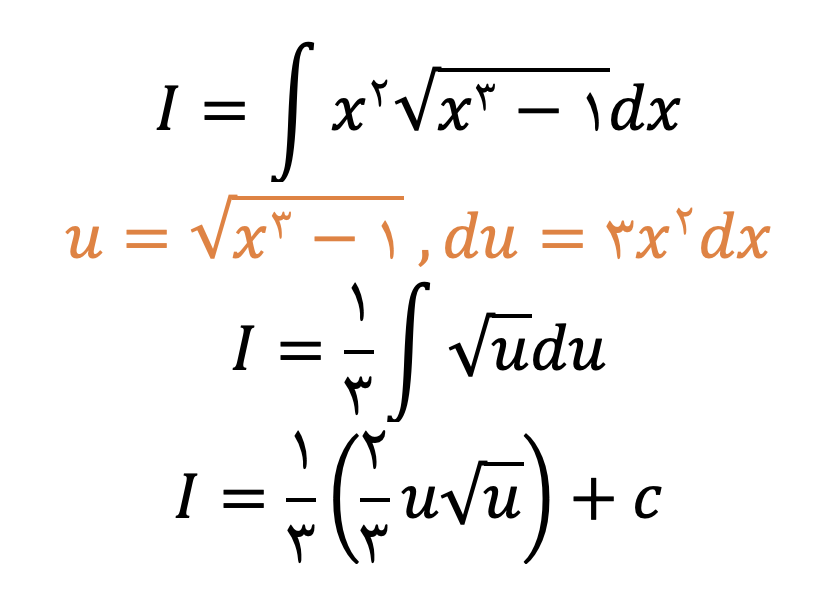
روش جزء به جزء
انتگرال جزء به جزء یک روش مخصوص برای انتگرالگیری از ضرب دو تابع متفاوت است. روش جزء به جزء معمولاً برای توابعی استفاده میشود که فرمول مستقیمی برای بهدستآوردن انتگرال آنها وجود ندارد؛ مثلاً فرمول انتگرال توابع هیپربولیکی با استفاده از انتگرالگیری جزء به جزء به دست میآید. فرمول روش انتگرال گیری جزء به جزء بهاین شکل است:
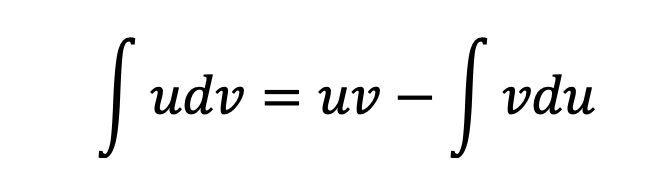
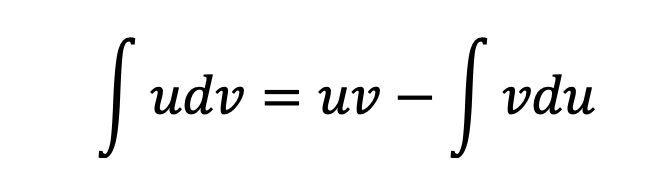
در برخی از حالتها بعد از محاسبهی این فرمول دوباره با انتگرالی مواجه میشویم که حل سادهای ندارد. در این حالت میتوانیم دوباره از روش جزء به جزء استفاده کنیم یا روش انتگرال گیری تغییرمتغیر را به کار ببریم.
نمونه سوال
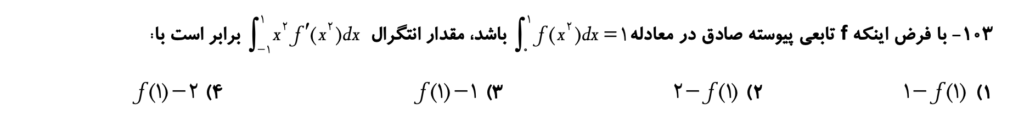
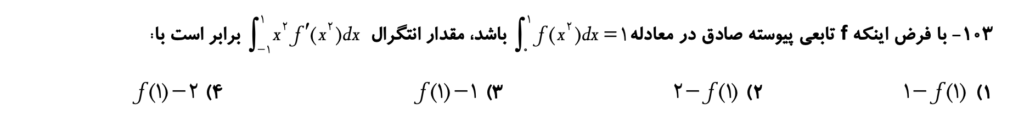


روش انتگرال گیری تفکیک کسر
این روش انتگرال گیری برای محاسبه انتگرالهای توابع گویا به کار میرود. هر گاه تابع انتگرال یک تابع کسری با مخرج به فرم حاصل چند تابع جبری داشته باشیم، برای سادهسازی انتگرالده کسر مدنظر را تفکیک میکنیم.
برای تفکیک کسر ابتدا مخرج را به فرم ضرب دو یا چند عبارت جبری تبدیل میکنیم و سپس باتوجه به صورت کسر، کسرها را از هم جدا میکنیم:


بعد از تفکیک کسرها هر یک را به صورت جداگانه محاسبه میکنیم.
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

