انتگرال سهگانه یک مفهوم پیچیده در ریاضیات است که در حوزههای مختلف فیزیک و ریاضیات بهکار میرود. این مفهوم ابتکاری از ریاضیدانان راجر پنروز و ریچارد فیشر است و اهمیت زیادی در فیزیک ذرات مییابد.
انتگرال سهگانه
در تعبیری ساده، انتگرال سهگانه بهمعنای اندازهگیری مقادیر میدان در یک نقطه وابسته به سه جهت فضایی است. این اندازهگیری در فیزیک ذرات جسمانی اهمیت خاصی دارد؛ زیرا این اطلاعات به ما کمک میکنند تا داینامیک و رفتار ذرات را در فضا درک کنیم.
کاربرد اصلی انتگرال سه گانه در فیزیک ذرات است، بهویژه در مطالعه جریانها و انتقال اطلاعات در این فضا. از این انتگرال برای محاسبه جرم، بار الکتریکی و مشخصههای دیگر ذرات استفاده میشود؛ همچنین در زمینههایی مانند الکتروداینامیک کوانتومی و مکانیک کوانتومی نیز کاربردهای گستردهای دارد.
بهطور خلاصه، انتگرال سهگانه یک ابزار قدرتمند در فهم عمیقتر ساختارهای ذرات و فرایندهای فیزیکی است که در مطالعه و تفسیر پدیدههای مختلف در دنیای زیراتمیک کمک بزرگی میکند. انتگرال دوگانه و انتگرال سهگانه هر دو مفاهیم ریاضیاتی مهم هستند، اما در زمینههای مختلف کاربرد دارند.
تفاوت انتگرال دوگانه و سهگانه در چیست؟
انتگرال دوگانه همچنین با نام انتگرال دوگانه محدودهٔ دوگانه و یا انتگرال دوگانه سطحی شناخته میشود. این نوع انتگرال به مفهوم اندازهگیری حجم زیر یک سطح دوبعدی در فضا میپردازد؛ مثلاً میتواند مفهوم حجم یک جسم سهبعدی را در فضا تا یک سطح معین اندازهگیری کند.
برای آشنایی بیشتر با انتگرال دوگانه این مطلب را مطالعه کنید:
درمقابل، انتگرال سهگانه به تحلیل و اندازهگیری میدانها و توزیعهای فیزیکی در فضاهای سهبعدی میپردازد. این نوع انتگرال به مفهوم اندازهگیری حجم یک فضای سهبعدی مرتبط است و در مطالعه فیزیک ذرات و جریانات فیزیکی اهمیت دارد.
بنابراین تفاوت اصلی میان انتگرال دوگانه و سهگانه در این است که یکی به اندازهگیری حجم زیر یک سطح دوبعدی محدود میشود و دیگری به اندازهگیری حجم در فضای سهبعدی توجه میکند.
مفهوم انتگرال سه گانه
در انتگرالهای ریاضی ۱ انتگرالگیری روی یک تابعِ تک متغیره انجام میشد. در انتگرال دوگانه بیان شد که ناحیه انتگرالگیری در دو بعد است؛ بههمین صورت، در انتگرال سهگانه نیز ناحیه انتگرالگیری بهشکلی سهبعدی در نظر گرفته میشود.
برای آشنایی با قواعد انتگرال در ریاضیات این مطلب را مطالعه کنید:
انتگرال و قواعد آن در ریاضیات چیست؟
درصورتیکه بخواهیم از تابعی سهمتغیره انتگرال بگیریم، آن را بهاین صورت نمایش میدهیم:
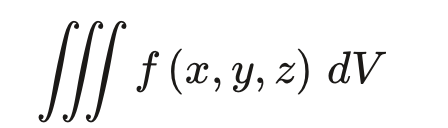
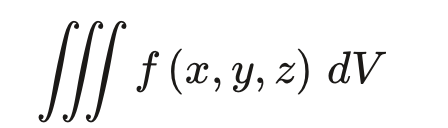
عناصر انتگرال سهگانه
هر المان حجم به ۶ صورت dxdydz، dxdzdy، dydxdz، dydzdx، dzdxdy و dzdydx باتوجه به کرانها میتواند بیان شود. ترتیب انتگرالگیری هم با توجه به ترتیب عناصر از داخل به خارج انجام میشود؛ برای مثال، در dxdydz ابتدا از تابع انتگرالگیری نسبت به x سپس نسبت به y و درنهایت نسبت به z انتگرال خواهیم گرفت.
نکات انتگرال سه گانه


انواع روشهای انتگرالگیری سهگانه
از سه روش برای محاسبه انتگرال سه گانه میتوانیم استفاده کنیم:
مختصات دکارتی
مختصات قطبی همان حل انتگرالها بهترتیب عناصر آن است. در انتگرالهای سه گانه اگر تابع نسبت به یک متغیر فرد باشد و در همان راستا هم متقارن باشد، مانند انتگرال های دیگر می توان آنها را صفر در نظر گرفت.
مختصات استوانهای
برای مختصات استوانهای از تغییر این متغیرها استفاده میکنیم:


در این حالت ابتدا در راستای zها انتگرال سهگانه گرفته شده و بعد باتوجه به شعاع و دایره دادهشده، مانند حالت قطبی در انتگرال دوگانه، انتگرالگیری را به پایان میرسانیم.
نمونه سوال
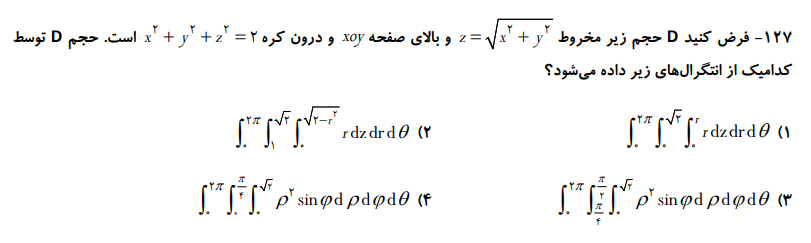
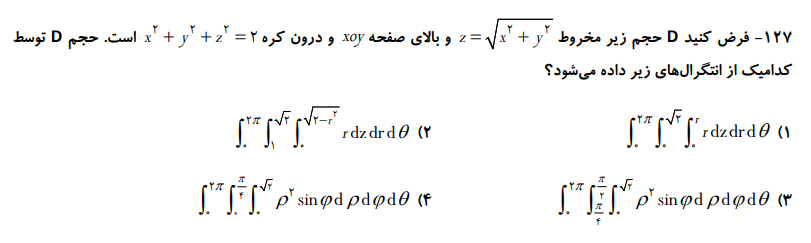
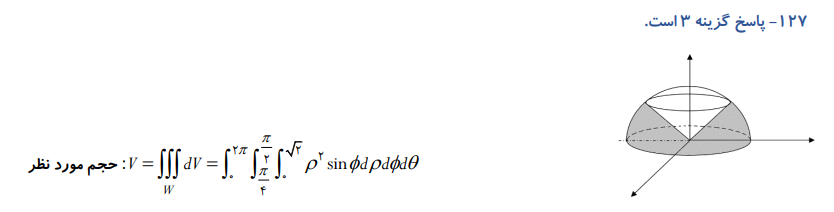
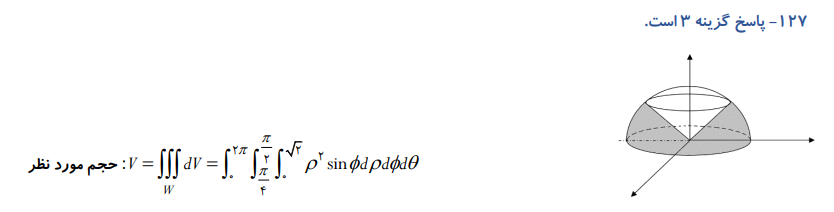
مختصات کروی
هر نقطه p(x,y,z) را در فضای سهبعدی میتوان در فرم کروی بهاین شکل در نظر گرفت. معمولاً در زمانی که ناحیه جواب یا تابع انتگرالده کروی باشد از این روش استفاده میکنیم.


کاربردهای انتگرال سهگانه
در ریاضی عمومی ۲ و بهطور کلی در فضای سهبعدی هر گاه بخواهیم حجم اجسام را محاسبه کنیم از انتگرال سه گانه استفاده می کنیم؛ همچنین برای محاسبه مرکز جرم یا گشتاور در فیزیک نیز از انتگرال سهگانه استفاده میشود.
مثال


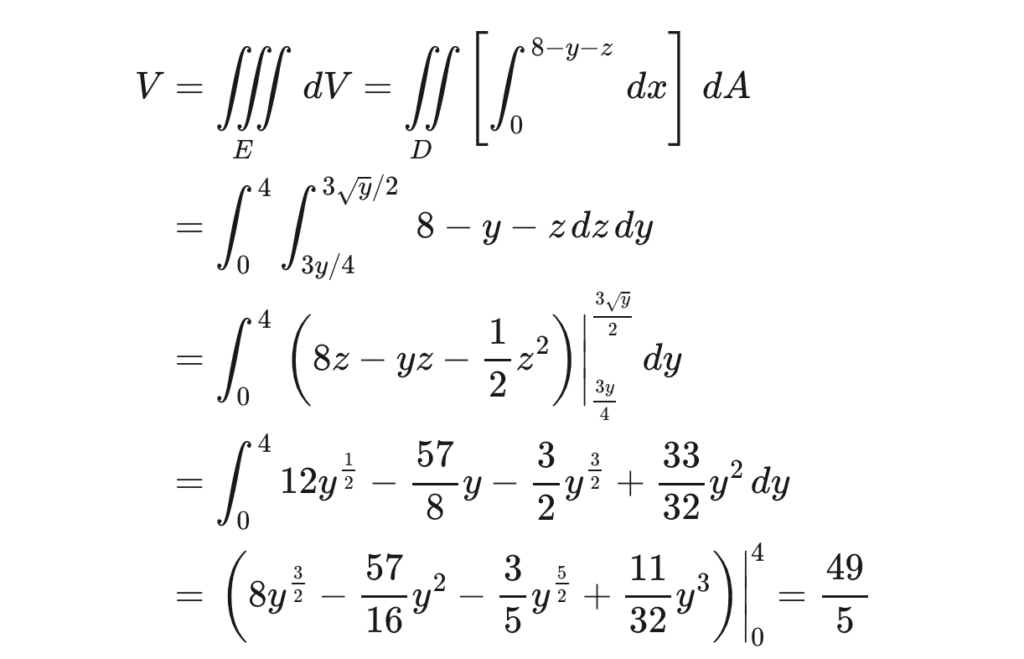
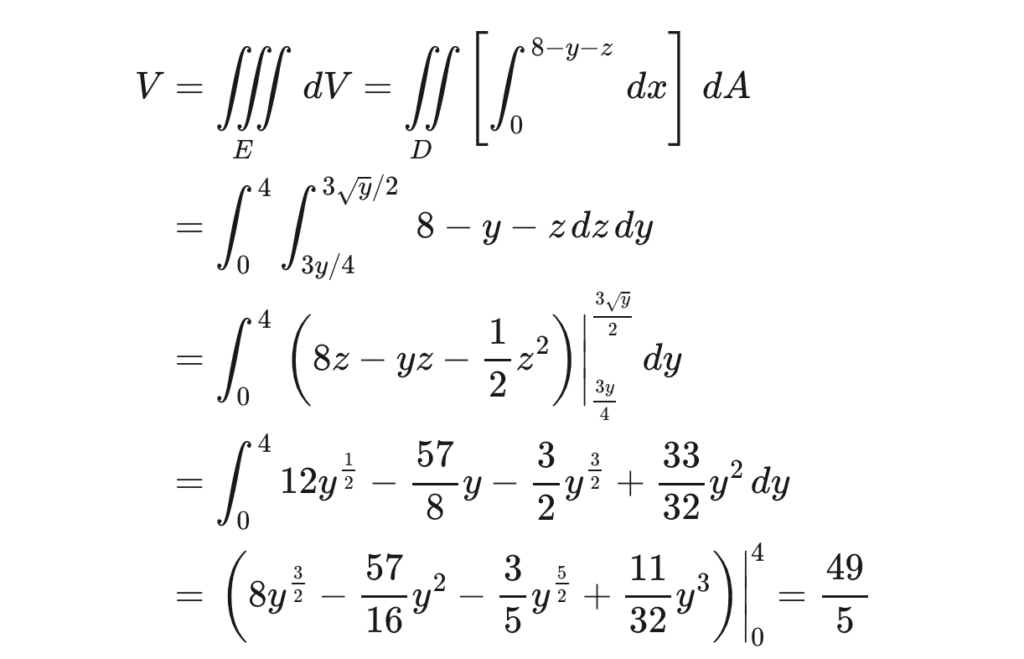
کلاس آنلاین ریاضی عمومی ۱ و ۲
برای موفقیت در کنکور کارشناسی ارشد مدیریت کسب و کار (MBA) و همینطور رشتههای مهندسی پیشنهاد ما شرکت در کلاسهای آنلاین ریاضی عمومی ۱ و ۲ است.
برای آشنایی با کلاس آنلاین ریاضی عمومی ۱ و ۲ و مشاوره رایگان در این باره روی این لینک کلیک کنید:

