تحلیل مؤلفههای اصلی یا PCA (Principal Component Analysis) یک تکنیک کاهش داده محبوب در یادگیری ماشین و از زیر گروه الگوریتمهای بدون ناظر است. از این الگوریتمها برای شناسایی الگوهای خطی در دادههای با ابعاد بالا استفاده میشود. در ادامه این مطلب، بهصورت دقیقتر این تکنیک، ازجمله پایههای ریاضی آن، کاربردهایش در دنیای واقعی و چگونگی پیادهسازی آن در محیطهای برنامهنویسی، را بررسی خواهیم کرد.
- 1. هدف از PCA یا تحلیل مؤلفههای اصلی چیست؟
- 2. پیشینه تاریخی PCA
- 3. ریاضیات پشت پرده تحلیل مؤلفههای اصلی
- 4. نقش تحلیل مؤلفههای اصلی (PCA) در یادگیری ماشین
- 5. بهینهسازی مدلهای یادگیری ماشین با کاهش فضای ویژگی توسط PCA
- 6. خطای بازسازی در تحلیل مؤلفههای اصلی (تابع هزینه PCA )
- 7. کاربردهای PCA در دنیای واقعی
- 8. محدودیتها و چالشهای PCA
- 9. مقایسه PCA با دیگر تکنیکهای کاهش ابعاد
- 10. قسمتی از جزوه کلاس برای آموزش الگوریتم PCA
- 11. پیادهسازی PCA در پایتون
- 12. جمعبندی درباره PCA یا تحلیل اجزای اصلی
-
13.
پرسشهای متداول
- 13.1. چه زمانی از تحلیل مؤلفههای اصلی (PCA) بهجای دیگر تکنیکهای کاهش ابعاد مانند t-SNE یا UMAP استفاده کنیم؟
- 13.2. آیا استفاده از PCA در تشخیص چهره در مقایسه با دیگر روشها مزایایی دارد؟
- 13.3. در چه مواردی استفاده از PCA ممکن است نتایج نامطلوبی داشته باشد؟
- 13.4. چگونه میتوانیم تعداد مؤلفههای اصلی (PCs) مناسب برای یک مدل را انتخاب کنیم؟
- 13.5. آیا PCA میتواند در تجزیهوتحلیل اسناد متنی کاربرد داشته باشد؟
- 14. یادگیری ماشین لرنینگ را از امروز شروع کنید!
- 15. هفتخوان: مطالعه کن، نظر بده، جایزه بگیر!
- 16. هفتخوانپلاس
هدف از PCA یا تحلیل مؤلفههای اصلی چیست؟
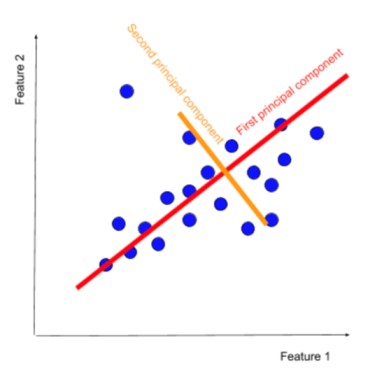
هدف اصلی PCA این است که یک فضای با ابعاد کمتر پیدا کند که بیشترین واریانس را در دادهها حفظ کند. این بهمعنای یافتن مجموعه ای از محورهای جدید است که بیشترین میزان پراکندگی دادهها را در خود جای می دهند.
این محورهای جدید بهعنوان مؤلفههای اصلی یا PC ها شناخته میشوند. PCA با کاهش ابعاد دادهها، پیچیدگی محاسباتی را کاهش میدهد و به بهبود کارایی الگوریتمهای یادگیری ماشین کمک میکند. همچنین با تمرکز بر مؤلفههای اصلی، نویز موجود در دادهها را کاهش میدهد و به بهبود دقت الگوریتمهای یادگیری ماشین کمک میکند. علاوهبراین، PCA با کاهش ابعاد دادهها، تجسم دادهها در فضای با ابعاد کمتر را تسهیل میکند.
از جنبههای کاربردی، PCA در بسیاری از زمینههای یادگیری ماشین استفاده میشود، ازجمله در کلاسبندی، خوشهبندی و دیگر مسائل تحلیلی. این روش، نهتنها باعث بهبود عملکرد مدلهای یادگیری ماشین میشود، بلکه به کاهش پیچیدگی محاسباتی و بهینهسازی فرایند آموزش نیز کمک میکند.

پیشینه تاریخی PCA
ریشههای تحلیل مؤلفههای اصلی (PCA) را میتوان در اوایل قرن بیستم جستوجو کرد. در سال ۱۹۰۱ کارل پیرسون (Karl Pearson)، ریاضیدان و زیستشناس بریتانیایی، مفهوم اصلی PCA را در مقاله خود با عنوان «On Lines and Planes of Closest Fit to System of Points in Space» معرفی کرد. پیرسون از PCA برای بررسی رابطه میان ویژگیهای مختلف در دادههای انسان استفاده کرد.
در دهههای ۱۹۳۰ هارولد هوتلینگ (Harold Hotelling)، آمارشناس امریکایی، PCA را بهطور مستقل توسعه داد و آن را بهعنوان یک روش آماری برای کاهش دادهها معرفی کرد. هوتلینگ PCA را در زمینههای مختلفی ازجمله روانشناسی، اقتصاد و علوم زیستی به کار برد. PCA از آن زمان بهبعد بهعنوان یک تکنیک کاهش داده محبوب در یادگیری ماشین تبدیل شده است و بهطور گسترده در زمینههای مختلف، مانند تشخیص الگو، تجزیه و تحلیل تصویر و پردازش زبان طبیعی، استفاده میشود.
ریاضیات پشت پرده تحلیل مؤلفههای اصلی
تحلیل مؤلفههای اصلی (PCA) بر پایه مفاهیم ریاضی، مانند ماتریس کواریانس، ارزشهای ویژه و بردارهای ویژه، قرار دارد. ماتریس کواریانس ماتریسی مربعی است که واریانس مشترک میان ویژگیهای مختلف در دادهها را نشان میدهد. ارزشهای ویژه ماتریس کواریانس نشاندهنده میزان واریانس موجود در هر جهت در فضای دادهها هستند. بردارهای ویژه ماتریس کواریانس جهتهایی را نشان میدهند که بیشترین میزان واریانس را در خود جای میدهند.
برای انجامدادن PCA این مرحلهها دنبال میشود:
- دادهها را استانداردسازی کنید: دادهها را بهگونهای استاندارد کنید که میانگین هر ویژگی صفر و واریانس آن یک باشد.
- کواریانس را محاسبه کنید: ماتریس کواریانس دادهها را محاسبه کنید.
- ارزشهای ویژه و بردارهای ویژه را محاسبه کنید: ارزشهای ویژه و بردارهای ویژه ماتریس کواریانس را محاسبه کنید.
- مهمترین PC ها را انتخاب کنید: مهمترین PC ها را با توجه به ارزشهای ویژه آنها انتخاب کنید.
- دادهها را به فضای جدید تبدیل کنید: دادهها را به فضای با ابعاد کمتر تشکیل شده توسط PC های انتخابی تبدیل کنید.
با دنبالکردن این مرحلهها، PCA میتواند ابعاد دادهها را بدون ازدستدادن اطلاعات مهم کاهش دهد و به بهبود کارایی الگوریتمهای یادگیری ماشین کمک کند.
نقش تحلیل مؤلفههای اصلی (PCA) در یادگیری ماشین
PCA با کاهش ابعاد دادهها، چندین مزیت را برای یادگیری ماشین به همراه دارد:
- کاهش پیچیدگی: با کاهش تعداد ویژگیها پیچیدگی محاسباتی را کاهش میدهد و به بهبود کارایی الگوریتمهای یادگیری ماشین کمک میکند. این امر، بهویژه، در هنگام کار با دادههای با ابعاد بالا مفید است؛ زیرا زیرا میتواند بهطور چشمگیری زمان محاسبات را کاهش دهد.
- کاهش نویز: با تمرکز بر PCها، نویز موجود در دادهها را کاهش میدهد. نویز میتواند بهطور قابل توجهی بر عملکرد الگوریتم های یادگیری ماشین تأثیر بگذارد؛ بنابراین کاهش نویز میتواند به بهبود دقت پیش بینی کمک کند.
- بهبود تجسم دادهها: با کاهش ابعاد دادهها، تجسم دادهها در فضای با ابعاد کمتر را تسهیل میکند. این امر میتواند به درک بهتر الگوها و روابط در دادهها کمک کند.
- کشف الگوهای پنهان: PCA میتواند به شناسایی الگوهای پنهان در داده های با ابعاد بالا کمک کند که ممکن است با روش های سنتی قابل مشاهده نباشند. این امر میتواند به بینش های جدید درمورد دادهها و بهبود عملکرد الگوریتمهای یادگیری ماشین بینجامد.
برای مطالعه بیشتر کلیک کنید:
شناسایی الگو (Pattern Recognition) چگونه کار میکند؟
بهینهسازی مدلهای یادگیری ماشین با کاهش فضای ویژگی توسط PCA
PCA با کاهش فضای ویژگی، مدلهای یادگیری ماشین را در چندین جنبه بهینه میکند:
- کاهش پیچیدگی مدل: با کاهش تعداد ویژگیها، تعداد پارامترهایی که مدل باید یاد بگیرد را کاهش می دهد که به کاهش پیچیدگی مدل میانجامد. مدلهای سادهتر معمولاً آموزش سریعتر و تعمیمپذیری بهتری دارند.
- کاهش بیشبرازش (Overfitting): با حذف ویژگیهای کماهمیت یا تکراری، PCA میتواند به کاهش بیش برازش کمک کند. بیشبرازش زمانی رخ می دهد که مدل بهشدت با دادههای آموزشی مطابقت میکند، اما عملکرد ضعیفی در دادههای جدید ناشناخته دارد.
- بهبود کارایی محاسباتی: با کاهش ابعاد دادهها PCA میتواند بهطور قابل توجهی زمان محاسبات را برای آموزش و پیشبینی مدلهای یادگیری ماشین کاهش دهد. این امر، بهویژه، در هنگام کار با داده های حجیم یا مدلهای پیچیده مفید است.
- بهبود تعمیمپذیری مدل: با تمرکز بر ویژگیهای مهمتر، PCA میتواند به بهبود تعمیمپذیری مدل کمک کند. تعمیمپذیری به توانایی مدل برای عملکرد خوب در دادههای جدید ناشناخته اشاره میکند.
خطای بازسازی در تحلیل مؤلفههای اصلی (تابع هزینه PCA )
یکی از جنبههای مهم در PCA درک مفهوم خطای بازسازی (Reconstruction Error) است. خطای بازسازی به میزان خطایی اشاره میکند که هنگام بازسازی دادههای اصلی از فضای با ابعاد کمتر ایجاد میشود. در PCA هدف این است که دادههای اصلی را با استفاده از فضای با ابعاد کمتر با دقت بالایی بازسازی کند. هرچه خطای بازسازی کمتر باشد، PCA بهتر میتواند دادههای اصلی را نشان دهد.
کاربردهای PCA در دنیای واقعی
برخی از کاربردهای PCA یا تحلیل مؤلفههای اصلی در دنیای واقعی از این قرار است:
تشخیص چهره
تشخیص چهره یکی از زمینههای کاربردی موفق PCA است. در این حوزه PCA برای کاهش ابعاد تصاویر چهره استفاده میشود تا الگوهای کلیدی چهره را شناسایی کند. این امر به الگوریتمهای یادگیری ماشین کمک میکند تا چهرهها را با دقت بیشتری شناسایی کنند، حتی در شرایط مختلف نورپردازی، زاویه و حالت چهره را.
تشخیص پزشکی
PCA را میتوان در تشخیص پزشکی برای تجزیهوتحلیل دادههای تصویربرداری، مانند MRI یا CT اسکن، استفاده کرد. با کاهش ابعاد تصاویر، PCA میتواند الگوهای پنهان را در تصاویر شناسایی کند که ممکن است با روشهای سنتی قابل مشاهده نباشند. این امر میتواند به تشخیص زودهنگام بیماریها و بهبود نتایج درمانی کمک کند.
توصیه محصولات
در سیستمهای توصیه محصولات، PCA برای تجزیهوتحلیل دادههای مشتری و محصول استفاده میشود. با کاهش ابعاد دادهها، PCA میتواند الگوهای خرید مشتریان را شناسایی کند و محصولات مرتبط را به آنها توصیه کند. این امر میتواند به بهبود تجربه کاربری و افزایش فروش کمک کند.
تجزیهوتحلیل متن
PCA را میتوان در تجزیهوتحلیل متن برای شناسایی الگوهای موضوعی در اسناد متنی استفاده کرد. با کاهش ابعاد متن، PCA میتواند موضوعات اصلی اسناد را شناسایی کند و آنها را به دستههای مختلف طبقهبندی کند. این امر میتواند به سازماندهی و بازیابی اطلاعات کمک کند.
کاهش ابعاد دادههای مرتبط با حسگرها
PCA را میتوان برای کاهش ابعاد دادههای حسگری از منابع مختلف مانند حسگرهای اینترنت اشیا (IoT) استفاده کرد. با کاهش ابعاد دادهها، PCA میتواند انتقال و پردازش دادهها را کارآمدتر کند و به تجزیهوتحلیل بهتر دادههای حسگری کمک کند.
علاوه بر نمونههای کاربردی ذکرشده، PCA در بسیاری از مطالعات موردی و پروژههای تحقیقاتی مثل تشخیص زودهنگام سرطان سینه و تشخیص تقلب در کارتهای اعتباری استفاده شده است.
محدودیتها و چالشهای PCA
برخی از محدودیتها و چالشهای PCA یا تحلیل مؤلفههای اصلی از این قرار است:
فرضیه خطیبودن دادهها
PCA براساس فرضیه خطیبودن دادهها کار میکند. این بهآن معناست که PCA فرض میکند که الگوهای میان ویژگیهای دادهها خطی هستند. درصورتیکه دادهها حاوی الگوهای غیرخطی باشند، PCA ممکن است عملکرد خوبی نداشته باشد.
حساسیت به نویز
PCA به نویز موجود در دادهها حساس است. نویز میتواند کاری کند که PCA الگوهای نادرست را در دادهها شناسایی کند. برای بهبود عملکرد PCA، مهم است که دادهها را قبل از اعمال PCA استانداردسازی یا نرمالسازی کنید.
تطابقنداشتن با دادههای نامتعادل
PCA برای دادههای نامتعادل که در آن تعداد نمونههای یک کلاس بهطور قابل توجهی بیشتر از تعداد نمونههای کلاس دیگر است مناسب نیست.
علاوه بر محدودیتهای گفتهشده، برخی چالشها مانند انتخاب تعداد مؤلفههای اصلی در استفاده از این الگوریتم وجود دارد. انتخاب تعداد مؤلفههای اصلی یکی از چالشهای مهم در استفاده از PCA است. انتخاب تعداد کم مؤلفههای اصلی ممکن است باعث ازدستدادن اطلاعات شود، درحالیکه انتخاب تعداد زیاد مؤلفههای اصلی ممکن است باعث بیشبرازش شود. بهصورت کلی اگر در pca = PCA(n_components)، مقدار n_components را برابر 95% قرار دهیم، PCA با درنظر گرفتن 95 درصد واریانس کار میکند و بهترین عملکرد را خواهد داشت.
مقایسه PCA با دیگر تکنیکهای کاهش ابعاد
در این بخش PCA را با سه تکنیک کاهش ابعاد دیگر، یعنی t-SNE، LDA و UMAP، مقایسه خواهیم کرد.
PCA در مقایسه با t-SNE
t-SNE یا t-Distributed Stochastic Neighbor Embedding یک تکنیک کاهش ابعاد غیرخطی است که برای حفظ ساختار محلی دادهها طراحی شده است، بهاین معنی که t-SNE تلاش میکند تا همسایگیهای محلی دادهها را در فضای با ابعاد کمتر حفظ کند. PCA، برعکس، یک تکنیک کاهش ابعاد خطی است که برای یافتن جهتهایی که بیشترین واریانس را در دادهها دارند طراحی شده است.
t-SNE معمولاً برای تجسم دادهها استفاده میشود؛ زیرا میتواند ساختار محلی دادهها را بهتر از PCA حفظ کند. PCA معمولاً برای کاهش ابعاد دادهها قبل از استفاده از الگوریتمهای یادگیری ماشین (Preprocessing) استفاده میشود؛ زیرا میتواند پیچیدگی محاسباتی را کاهش دهد.
PCA در مقایسه با LDA
LDA یا Linear Discriminant Analysis یک تکنیک کاهش ابعاد باناظر (Supervised) است که برای جداسازی میان کلاسهای مختلف در دادهها طراحی شده است. LDA تلاش میکند تا جهتهایی را پیدا کند که بیشترین جدایی را یان کلاسها ایجاد کنند؛ PCA، برعکس، یک تکنیک کاهش ابعاد بدون نظارت است که برای یافتن جهتهایی که بیشترین واریانس را در دادهها دارند طراحی شده است.
PCA در مقایسه با UMAP
UMAP یا Uniform Manifold Approximation and Projection یک تکنیک کاهش ابعاد غیرخطی است که برای حفظ ساختار محلی و کلی دادهها طراحی شده است، بهاین معنی که UMAP تلاش میکند تا همسایگیهای محلی دادهها و روابط میان نقاط دورتر را در فضای با ابعاد کمتر حفظ کند؛ PCA، برعکس، یک تکنیک کاهش ابعاد خطی است که برای یافتن جهتهایی که بیشترین واریانس را در دادهها دارند طراحی شده است و پیچیدگی محاسباتی را کاهش میدهد.
چه زمانی از PCA استفاده کنیم؟ زمانی که دادهها خطی هستند، ابعاد (Features) زیاد و نویز کمی دارند؛ استفاده از این الگوریتم پیشنهاد میشود.
چه زمانی از تکنیکهای دیگر استفاده کنیم؟ اگر دادهها حاوی الگوهای غیرخطی هستند، از t-SNE یا UMAP استفاده میکنیم؛ همچنین اگر دادهها طبقهبندی شدهاند، LDA ممکن است مناسبتر از PCA باشد.
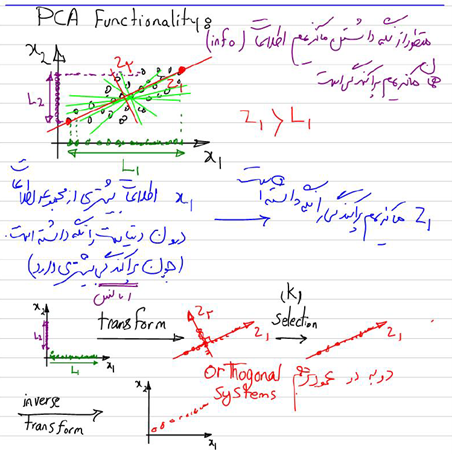
قسمتی از جزوه کلاس برای آموزش الگوریتم PCA

پیادهسازی PCA در پایتون
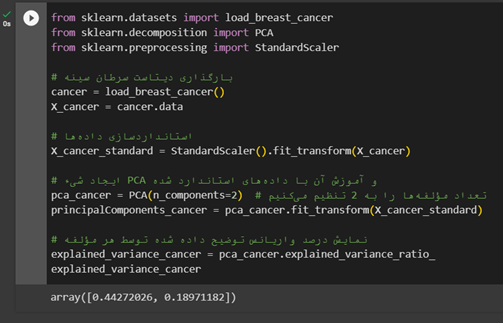
PCA بر روی دیتاست سرطان سینه اجرا شده است. نتایج نشان میدهد که اولین مؤلفه اصلی حدود 44.27 درصد و دومین مؤلفه اصلی حدود 18.97 درصد از واریانس کل دادههای این دیتاست را توضیح میدهند. این مقادیر بیانگر توانایی PCA در کاهش ابعاد دادههای پیچیدهای مانند دادههای سرطان سینه، ضمن حفظ نسبتاً بالایی از واریانس اصلی دادههاست.

جمعبندی درباره PCA یا تحلیل اجزای اصلی
در این مطلب ما بهصورت جامع جامع تحلیل مؤلفههای اصلی یا PCA را بررسی کردیم. تحلیل مؤلفههای اصلی (Principal Component Analysis) یک تکنیک کاهش ابعاد قدرتمند است که میتواند برای انواع مختلفی از دادهها استفاده شود. PCA، با کاهش ابعاد دادهها، پیچیدگی را کاهش میدهد، کارایی الگوریتمهای یادگیری ماشین را بهبود میبخشد و تجسم دادهها در فضای با ابعاد کمتر را تسهیل میکند.
پرسشهای متداول
چه زمانی از تحلیل مؤلفههای اصلی (PCA) بهجای دیگر تکنیکهای کاهش ابعاد مانند t-SNE یا UMAP استفاده کنیم؟
PCA برای دادههایی با الگوهای خطی و ابعاد بالا مناسب است، بهخصوص زمانی که نیاز به کاهش پیچیدگی محاسباتی و افزایش کارایی الگوریتمها دارید؛ درمقابل، t-SNE و UMAP برای دادههای با الگوهای غیرخطی و حفظ ساختار محلی دادهها بهتر عمل میکنند.
آیا استفاده از PCA در تشخیص چهره در مقایسه با دیگر روشها مزایایی دارد؟
بله، PCA با کاهش ابعاد تصاویر چهره و تمرکز بر الگوهای کلیدی، به الگوریتمهای یادگیری ماشین کمک میکند تا چهرهها را در شرایط نورپردازی و زاویههای مختلف با دقت بیشتر شناسایی کنند.
در چه مواردی استفاده از PCA ممکن است نتایج نامطلوبی داشته باشد؟
PCA درصورتیکه دادهها دارای الگوهای غیرخطی باشند یا نویز زیادی داشته باشند، ممکن است نتایج نامطلوبی ارائه کند؛ همچنین در دادههای نامتعادل که تعداد نمونههای یک کلاس به طور قابل توجهی بیشتر است، ممکن است کارایی خوبی نداشته باشد.
چگونه میتوانیم تعداد مؤلفههای اصلی (PCs) مناسب برای یک مدل را انتخاب کنیم؟
انتخاب تعداد مناسب مؤلفههای اصلی به واریانسی بستگی دارد که میخواهید در مدل خود حفظ کنید. معمولاً با تجزیهوتحلیل ماتریس کواریانس و محاسبه ارزشهای ویژه میتوانید تعداد مؤلفههای اصلی را براساس درصدی از واریانس کل دادهها که میخواهید حفظ شود انتخاب کنید.
آیا PCA میتواند در تجزیهوتحلیل اسناد متنی کاربرد داشته باشد؟
بله، PCA میتواند در تجزیهوتحلیل متن به شناسایی الگوهای موضوعی کمک کند. با کاهش ابعاد متن PCA به شناسایی موضوعهای اصلی و طبقهبندی اسناد متنی به دستههای مختلف کمک میکند، این امر در سازماندهی و بازیابی اطلاعات بسیار مفید است.
یادگیری ماشین لرنینگ را از امروز شروع کنید!
دنیای دادهها جذاب است و دانستن علم داده، توانایی تحلیل داده یا بازاریابی مبتنی بر داده، شما را برای فرصتهای شغلی بسیاری مناسب میکند. فارغ از رشته و پیشزمینه، میتوانید حالا شروع کنید و از سطح مقدماتی تا پیشرفته بیاموزید. اگر دوست دارید به این حوزه وارد شوید، پیشنهاد میکنیم با کلیک روی این لینک قدم اول را همین حالا بردارید.
مشاوران کافهتدریس به شما کمک میکنند مسیر یادگیری برای ورود به این حوزه را شروع کنید:
دوره جامع دیتا ساینس و ماشین لرنینگ


هفتخوان: مطالعه کن، نظر بده، جایزه بگیر!
هفتخوان مسابقهی وبلاگی کافهتدریس است. شما با پاسخ به چند پرسش دربارهی مطلبی که همین حالا مطالعه کردهاید، فرصت شرکت در قرعهکشی جایزه نقدی و کلاس رایگان کافهتدریس را پیدا خواهید کرد.
جوایز هفتخوان
- ۱,۵۰۰,۰۰۰ تومان جایزه نقدی
- ۳ کلاس رایگان ۵۰۰,۰۰۰ تومانی
پرسشهای مسابقه
برای شرکت در هفتخوان کافهتدریس در کامنت همین مطلب به این پرسشها پاسخ دهید:
- هدف از استفاده از تحلیل مؤلفههای اصلی (PCA) در پردازش دادهها چیست؟
- در بین کاربردهای مختلف PCA، کدام یک بیشتر با علم پزشکی ارتباط دارد؟
- تفاوت اصلی بین PCA و t-SNE در چیست و کدام یک برای کاهش ابعاد دادههای بسیار پیچیده مناسبتر است؟
هفتخوانپلاس
برای بالابردن شانستان میتوانید این مطلب را هم مطالعه کنید و به پرسشهای آن پاسخ دهید:


هدف از استفاده از تحلیل مؤلفههای اصلی (PCA) در پردازش دادهها چیست؟
هدف اصلی PCA این است که یک فضای با ابعاد کمتر پیدا کند که بیشترین واریانس را در دادهها حفظ کند. این بهمعنای یافتن مجموعه ای از محورهای جدید است که بیشترین میزان پراکندگی دادهها را در خود جای می دهند.
این محورهای جدید بهعنوان مؤلفههای اصلی یا PC ها شناخته میشوند. PCA با کاهش ابعاد دادهها، پیچیدگی محاسباتی را کاهش میدهد و به بهبود کارایی الگوریتمهای یادگیری ماشین کمک میکند. همچنین با تمرکز بر مؤلفههای اصلی، نویز موجود در دادهها را کاهش میدهد و به بهبود دقت الگوریتمهای یادگیری ماشین کمک میکند. علاوهبراین، PCA با کاهش ابعاد دادهها، تجسم دادهها در فضای با ابعاد کمتر را تسهیل میکند.
در بین کاربردهای مختلف PCA، کدام یک بیشتر با علم پزشکی ارتباط دارد؟
PCA را میتوان در تشخیص پزشکی برای تجزیهوتحلیل دادههای تصویربرداری، مانند MRI یا CT اسکن، استفاده کردبا کاهش ابعاد تصاویر، PCA میتواند الگوهای پنهان را در تصاویر شناسایی کند که ممکن است با روشهای سنتی قابل مشاهده نباشند
تفاوت اصلی بین PCA و t-SNE در چیست و کدام یک برای کاهش ابعاد دادههای بسیار پیچیده مناسبتر است؟
PCA برای دادههایی با الگوهای خطی و ابعاد بالا مناسب است، بهخصوص زمانی که نیاز به کاهش پیچیدگی محاسباتی و افزایش کارایی الگوریتمها دارید؛ درمقابل، t-SNE و UMAP برای دادههای با الگوهای غیرخطی و حفظ ساختار محلی دادهها بهتر عمل میکنند.
سوال ۳:
۳.۲
PCA معمولاً برای کاهش ابعاد دادهها قبل از استفاده از الگوریتمهای یادگیری ماشین (Preprocessing) استفاده میشود؛ زیرا میتواند پیچیدگی محاسباتی را کاهش دهد.
۳.۱
t-sne یک تکنیک کاهش ابعاد غیرخطی است ،
PCA، برعکس، یک تکنیک کاهش ابعاد خطی است
سوال ۲:
تشخیص پزشکی
PCA را میتوان در تشخیص پزشکی برای تجزیهوتحلیل دادههای تصویربرداری، مانند MRI یا CT اسکن، استفاده کرد. با کاهش ابعاد تصاویر، PCA میتواند الگوهای پنهان را در تصاویر شناسایی کند که ممکن است با روشهای سنتی قابل مشاهده نباشند
سوال۱:
هدف اصلی PCA این است که یک فضای با ابعاد کمتر پیدا کند که بیشترین واریانس را در دادهها حفظ کند. این بهمعنای یافتن مجموعه ای از محورهای جدید است که بیشترین میزان پراکندگی دادهها را در خود جای می دهند.
این محورهای جدید بهعنوان مؤلفههای اصلی یا PC ها شناخته میشوند