با الگوریتم K نزدیک ترین همسایه (K-Nearest Neighbors) آشنا شوید!

الگوریتم K نزدیک ترین همسایه (K-Nearest Neighbors) که به‌اختصار به آن KNN نیز گفته می‌شود یک الگوریتم یادگیری ماشین با ناظر ساده (Supervised Machine Learning) و با پیاده‌سازی آسان است. این الگوریتم می‌تواند برای حل مشکلات طبقه‌بندی (Classification) و رگرسیون (Regression) استفاده شود.

نگاهی مختصر به یادگیری باناظر

یک الگوریتم یادگیری ماشین باناظر الگوریتمی است که بر داده‌های ورودی دارای برچسب متکی است تا از روی این داده‌ها آموزش ببیند و بتواند آن‌ها را برچسب‌گذاری کند.

تصور کنید کامپیوتر یک کودک است، ما سرپرست آن هستیم (برای مثال والدین، یا معلم). ما می‌خواهیم کودک (کامپیوتر) بیاموزد گربه چه شکلی دارد. ما چندین تصویر مختلف را به کودک نشان می‌دهیم که برخی از آن‌ها گربه هستند و باقی می‌توانند تصاویر هر چیزی غیر از گربه باشند.

وقتی گربه را می‌بینیم می‌گوییم «گربه!»؛ وقتی گربه نباشد، به او می‌گوییم «نه، این گربه نیست!». پس از چندین بار انجام‌دادن این کار با کودک، ما یک عکس به او نشان می‌دهیم و می‌پرسیم «آیا این گربه است؟» و او، بسته به اینکه تصویر چیست، می‌گوید «گربه!» یا «نه، این گربه نیست!»؛ این همان یادگیری ماشین باناظر است. الگوریتم‌های یادگیری ماشین باناظر برای حل مسائل طبقه‌بندی (Classification)‌ یا رگرسیون (Regression) استفاده می‌شوند.

برای مطالعه بیشتر در این باره پیشنهاد می‌کنیم این مطلب را هم مطالعه کنید:

یادگیری با ناظر (Supervised Learning) چیست؟

الگوریتم K نزدیک ترین همسایه (K-Nearest Neighbors)

الگوریتم K نزدیک ترین همسایه یا KNN یکی از ساده‌ترین الگوریتم‌های یادگیری ماشین باناظر است که برای حل مسائل طبقه‌بندی و رگرسیون استفاده می‌شود.

KNN هم‌چنین به‌عنوان یک مدل مبتنی بر نمونه (instance-based method) یا یک یادگیرنده‌ی تنبل (lazy learner)‌ شناخته می‌شود؛ زیرا یک مدل داخلی ایجاد نمی‌کند و از داده‌های آموزش عملکرد متمایز را یاد نمی‌گیرد؛ فقط نمونه‌های آموزشی را حفظ می‌کند که به‌عنوان «دانش» برای مرحله‌ی پیش‌بینی استفاده می‌شود.

این الگوریتم برای مسائل طبقه‌بندی k نزدیک ترین همسایه را پیدا و با اکثریت آرا نزدیک‌ترین همسایگان کلاس را پیش‌بینی می‌کند.

برای مسائل رگرسیون k نزدیک‌ترین همسایه را پیدا و با محاسبه‌ی میانگین مقدار نزدیک‌ترین همسایه‌ها، مقدار مدنظر را پیش‌بینی می‌کند.

مراحل الگوریتم K نزدیک‌ترین همسایه

بیایید با هم مراحل این الگوریتم را بررسی کنیم:

1. داده‌ها را بارگذاری می‌کنیم.
2. مقدار K را تعیین می‌کنیم که همان تعداد نزدیک‌ترین همسایه‌ها هستند.
3. برای هر نمونه داده:
   • فاصله‌ی میان نمونه داده‌ی جدید را با نمونه داده‌های موجود محاسبه می‌کنیم.
   • فاصله و شاخص هر نمونه را به یک فهرست وارد می‌کنیم.
4. کل لیست را براساس فاصله‌ی نمونه داده‌ها، از کمترین به بیشترین فاصله، مرتب می‌کنیم.
5. K تا از اولین نمونه‌های فهرست مرتب‌شده را به‌عنوان K نزدیک‌ترین همسایه انتخاب می‌کنیم.
6. برچسب این K نمونه را بررسی می‌کنیم.
7. اگر مسئله رگرسیون باشد، میانگین برچسب‌های این K نمونه داده برچسب نمونه داده جدیدمان خواهد بود.
8. درصورتی‌که مسئله طبقه‌بندی باشد، نمونه‌ی جدید هم همان برچسب K همسایه را خواهد داشت.

قطعاً بعد از دیدن این الگوریتم، از اولین سوالاتی که برایمان پیش می‌آید این است که اولاً مقدار K را چگونه انتخاب کنیم و دوماً چطور این نزدیکترین همسایه‌ها را پیدا کنیم. در ادامه پاسخ این دو سؤال را خواهیم یافت.

چطور مقدار بهینه K یا Optimal K Value را پیدا کنیم؟

انتخاب مقدار مناسب K تنظیم پارامتر نامیده می‌شود و برای نتایج بهتر ضروری است. برای انتخاب مقدار K ریشه‌ی مربع یا همان جذر یا رادیکال تعداد کل نقاط داده‌ی موجود در مجموعه‌ی داده را حساب می‌کنیم.

این موضوع را در نظر بگیرید که درنهایت مقدار فرد K همیشه برای جلوگیری از سردرگمی میان دو کلاس انتخاب می‌شود.

چطور نزدیک‌ترین همسایه‌ها را پیدا کنیم؟

تکنیک‌های مختلفی برای یافتن k نزدیک‌ترین همسایه وجود دارد:

• فاصله‌ی اقلیدسی (Euclidean distance)
• فاصله‌ی منهتن (Manhattan distance)
• فاصله‌ی مینکوفسکی (Minkowski distance)

یکی از تکنیک‌هایی که بسیار استفاده می‌شود فاصله‌ی اقلیدسی است.

فاصله‌ی اقلیدسی برای محاسبه‌ی فاصله‌ی میان دو نقطه در یک صفحه یا یک فضای سه‌بعدی استفاده می‌شود. فاصله‌ی اقلیدسی براساس قضیه‌ی فیثاغورس است.

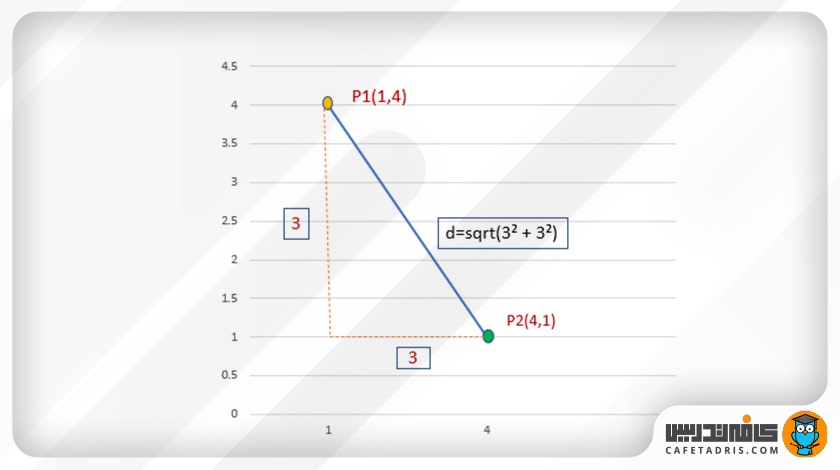
بیایید فاصله‌ی میان P1 و P2 را محاسبه کنیم:

P1 و (1،4)P2 (4،1)

قضیه‌ی فیثاغورس

در هر مثلث راست‌گوشه یا قائم‌الزاویه مربع وتر (طولانی‌ترین ضلع مثلث) برابر است با مجموع مربع دو ضلع دیگر مثلث.

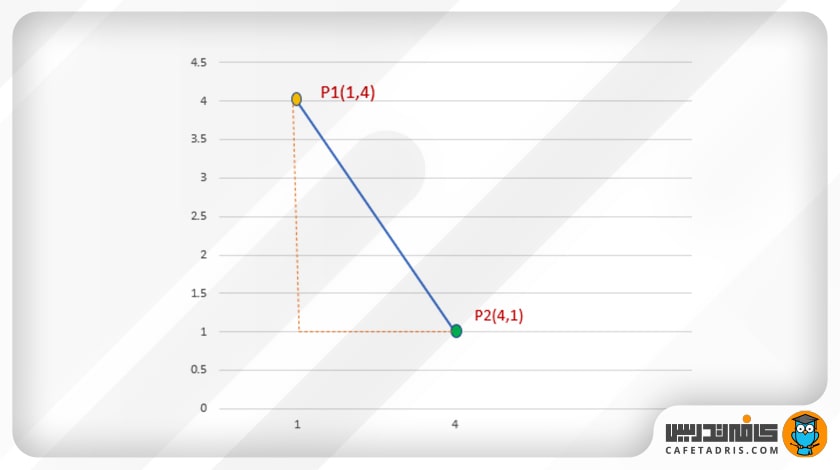
a² + b² = c²

→ c² = a² + b²
→ c= sqrt(a²+b²)

فرمول فاصله‌ی اقلیدسی از قضیه‌ی فیثاغورس مشتق شده است:

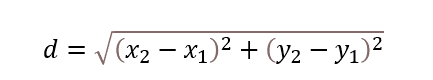
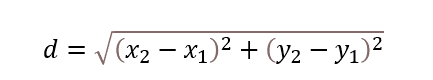
اکنون می‌توانیم فاصله‌ی میان دو نقطه‌ی P1 (1،4) و P2 (4،1) را با استفاده از فرمول فاصله‌ی اقلیدسی محاسبه کنیم.

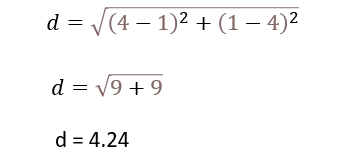
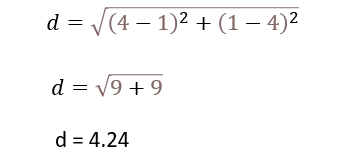
طبقه‌بندی با K نزدیک‌ترین همسایه

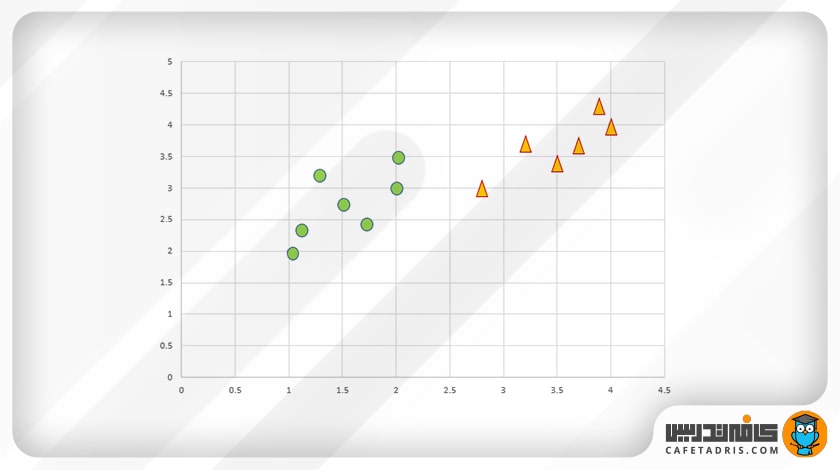
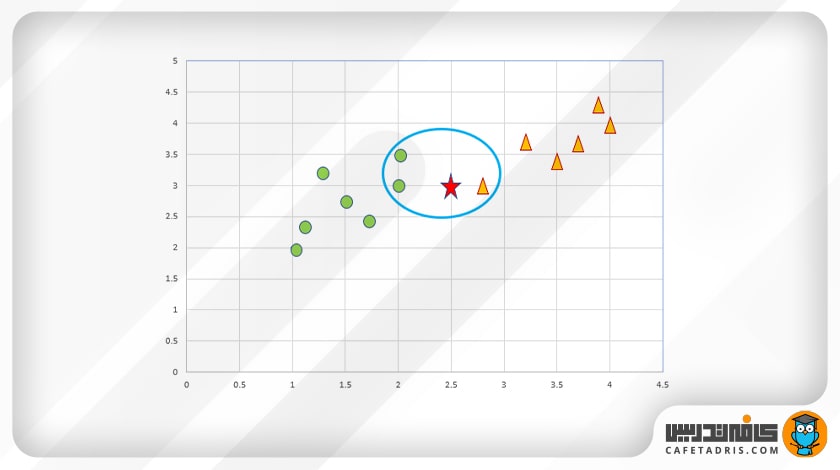
بیایید نحوه‌ی طبقه‌بندی داده‌ها با استفاده از الگوریتم KNN را بیاموزیم. فرض کنید دو کلاس داریم دایره و مثلث.

در این شکل نمایش نقاط داده در فضای ویژگی‌ها آمده است:

حال باید کلاس داده‌ی جدید را پیش‌بینی کنیم (شکل ستاره). ما باید پیش‌بینی کنیم که داده‌ی جدید (شکل ستاره) به کلاس دایره تعلق دارد یا کلاس مثلث.

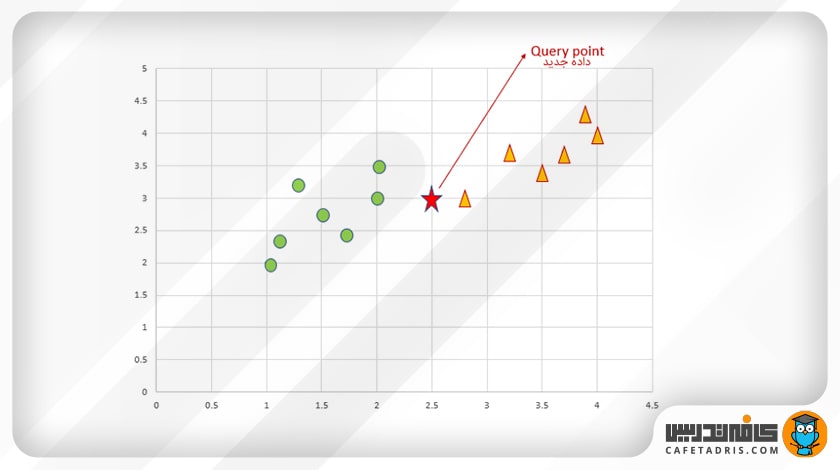
ابتدا باید مقدار k را تعیین کنیم. k تعداد نزدیک‌ترین همسایه‌ها را نشان می‌دهد.

در مرحله‌ی دوم باید K نزدیک‌ترین همسایه را براساس فاصله تعیین کنیم.

در این مثال، نزدیک‌ترین همسایه‌ها در داخل بیضی آبی نشان داده شده‌اند. همان‌طور که می‌بینیم، اکثریت داده‌ها به کلاس دایره متعلق است؛ بنابراین داده‌ی جدید به کلاس دایره متعلق خواهد بود.

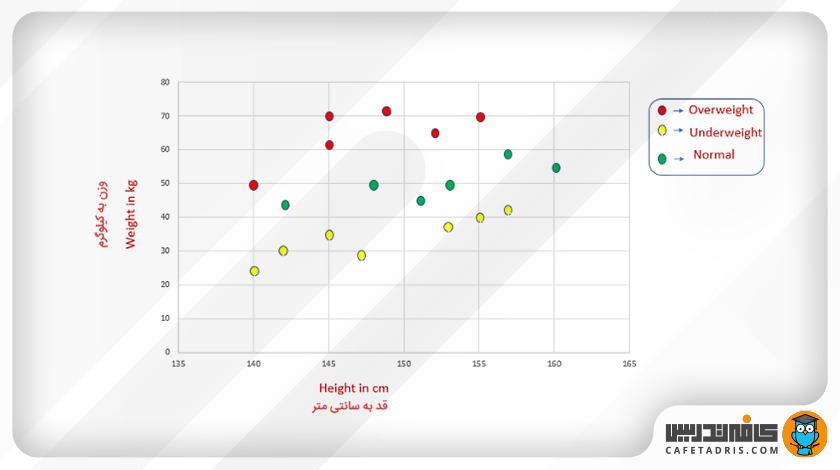
اعمال KNN روی یک دیتاست

در اینجا یک مجموعه داده‌ی کوچک داریم که ویژگی‌های قد و وزن و متغیر هدف BMI را شامل است. درواقع هر فرد با توجه به قد و وزنش در یکی از سه کلاس اضافه‌وزن (Overweight)، کمبود وزن (Underweight) یا نرمال (Normal)‌ قرار می‌گیرد.

در این شکل نمایش داده‌ها در فضای ویژگی را می‌بینیم.

حال بیایید پیش‌بینی کنیم BMI یک فرد برای یک قد و وزن خاص چقدر است؟

یک داده جدید به داده‌های موجود اضافه می‌شود که در شکل بعد با ستاره مشخص شده است. همان‌طور که می‌بینیم قد این فرد برابر با ۱۵۰ و وزنش ۶۰ کیلوگرم است.

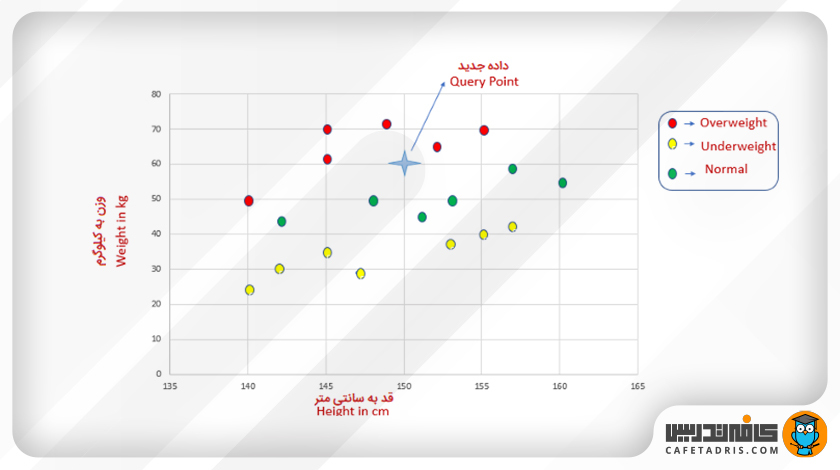
بیایید پیش‌بینی کنیم این فرد به کلاس «اضافه‌وزن»، «نرمال» یا «کمبود وز» تعلق دارد.

اول باید فاصله‌ی اقلیدسی را محاسبه کنیم و نزدیک‌ترین همسایه‌های آن را پیدا کنیم.

محاسبه‌ی فاصله‌ی اقلیدسی

با استفاده از فرمول فاصله‌ی اقلیدسی فاصله‌ی میان نقاط داده و داده‌ی جدید را محاسبه می‌کنیم. پس از محاسبه‌ی فاصله برای تمامی نقاط داده آن را مرتب و k نزدیک‌ترین همسایه را که کوتاه‌ترین فاصله را دارند پیدا می‌کنیم.

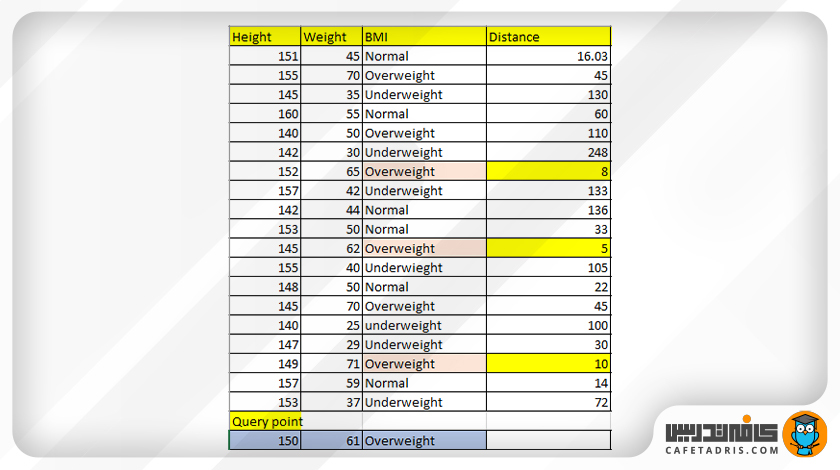
همسایه‌های نزدیک این داده با توجه به جدول بالا به‌راحتی پیدا شد. در اینجا مقدار K‌ برابر با ۳ است. در این شکل می‌توانیم این همسایه‌ها را ببینیم که در بیضی مشخص شده‌اند:

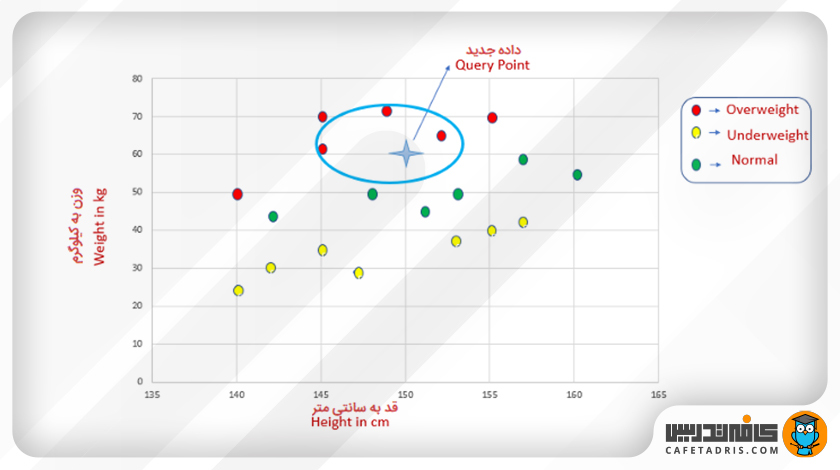
از میان ۳ همسایه نزدیک، هر ۳ آن‌ها به کلاس «اضافه‌وزن» متعلق هستند؛ بنابراین فردی که قد او ۱۵۰ سانتی‌متر و وزن ۶۱ کیلوگرم دارد به کلاس «اضافه‌وزن» متعلق است.

محاسبه‌ی فاصله‌ی منهتن (Manhattan Distance)

فاصله منهتن یکی از روش‌های محاسبه فاصله در الگوریتم KNN است که به ویژه در مسائلی که مسیرهای جابه‌جایی مهم هستند، کاربرد دارد.

تعریف فاصله منهتن

فاصله منهتن بین دو نقطه با مختصات  (x_1, y_1) و (x_2, y_2) ، برابر با مجموع مطلق اختلافات مختصات آنها است:

 

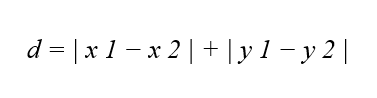
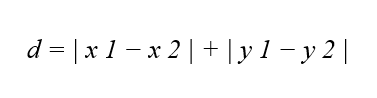
استفاده در KNN

فاصله منهتن به ویژه در مواقعی که نیاز به محاسبه مسیرهای جابه‌جایی یا مسافت حضور ویژگی‌ها در فضا داریم، کاربرد دارد. برای مثال، اگر ویژگی‌ها مربوط به محل قرارگیری در یک شبکه شهری باشند، فاصله منهتن مناسب‌ترین انتخاب خواهد بود. این فاصله به خوبی مفهوم مسافت مسیرهای عمودی و افقی بین دو نقطه را نشان می‌دهد.

مثال عملی

برای دو نمونه داده با مختصات (3, 4) و (6, 8) ، فاصله منهتن به صورت زیر محاسبه می‌شود:

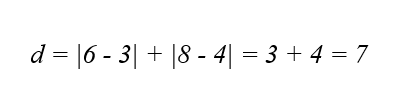
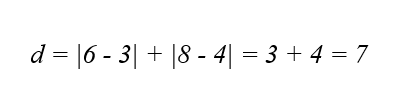
محاسبه‌ی فاصله‌ی مینکوفسکی (Minkowski Distance)

فاصله مینکوفسکی یک معیار کلی برای اندازه‌گیری فاصله بین دو نقطه در فضای چند ویژگی (فضای n-بعدی) است و به ویژه در مواقعی که نیاز به تنظیم وزن مختلف برای ویژگی‌ها وجود دارد، کاربرد دارد. این فاصله یک تعمیم از فاصله اقلیدسی و فاصله منهتن است و با استفاده از یک پارامتر قابل تنظیم به نام p محاسبه می‌شود. فرمول کلی فاصله مینکوفسکی بین دو نقطه با مختصات

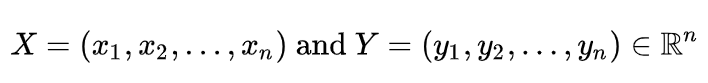
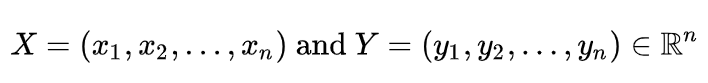
به شکل زیر است

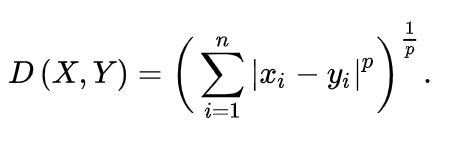
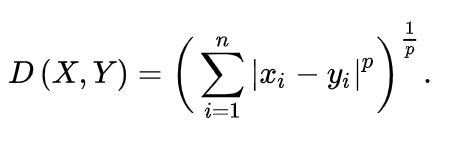
در اینجا n تعداد ویژگی‌ها است. مقدار پارامتر p تعیین کننده شکل فاصله است. زمانی که p=2 باشد، فاصله مینکوفسکی به فاصله اقلیدسی تبدیل می‌شود و زمانی که p=1 باشد، به فاصله منهتن معادل خواهد بود.

قسمتی از جزوه کلاس برای آموزش الگوریتم KNN

دوره جامع دیتا ساینس و ماشین لرنینگ

انجام یک تسک ساده با الگوریتم KNN

جمع‌بندی مطالب درباره‌ی K نزدیک ترین همسایه (K-Nearest Neighbors)

در این مقاله الگوریتم K نزدیک ترین همسایه (KNN) را معرفی کردیم که یک الگوریتم یادگیری باناظر (Supervised Learning)‌ است. از آنجا که الگوریتم KNN فقط دو پارامتر تنظیم دارد، پیاده‌سازی راحتی دارد و هم در مسائل طبقه‌بندی و هم مسائل رگرسیون استفاده می‌شود. نکته‌ی مهم این است که بدانیم بهتر است زمانی از الگوریتم KNN استفاده کنیم که دیتاست کوچکی داریم و داده‌های آن به‌درستی برچسب‌گذاری شده‌اند و دیتاست هم نویز (Noise)‌ چندانی ندارد؛ زیرا اگر داده‌ای اشتباه طبقه‌بندی شده باشد، احتمال اینکه داده‌ی جدید ما هم اشتباه طبقه‌بندی شود زیاد است. از آنجا که الگوریتم KNN یک نوع الگوریتم یادگیری ماشین باناظر است، بهتر است برای درک بهتر این مقاله را مطالعه کنید:‌

یادگیری ماشین (Machine Learning) چیست و چگونه کار می‌کند؟

یادگیری دیتا ساینس و ماشین لرنینگ با کلاس‌های آنلاین آموزش علم داده کافه‌تدریس

یکی از بهترین روش‌ها برای یادگیری علم داده و یادگیری ماشین شرکت در کلاس‌های آنلاین آموزش دیتا ساینس است. کافه‌تدریس با استفاده از به‌روزترین و جامع‌ترین روش‌های آموزشی، کلاس‌های آنلاین آموزش علم داده را برگزار می‌کند.

کلاس‌های آنلاین علم داده کافه‌تدریس در دوره‌های مقدماتی و پیشرفته برگزار می‌شود و شکل برگزاری آن به‌صورت کارگاهی و مبتنی بر کار روی پروژه‌های واقعی علم داده است.

برای آشنایی با کلاس‌های آنلاین آموزش علم داده کافه‌تدریس و مشاوره‌ی رایگان برای شروع یادگیری دیتا ساینس و ماشین لرنینگ روی این لینک کلیک کنید:

کلاس‌های آنلاین علم داده کافه‌تدریس