پاسخ پرسش نُرم چیست در ابتدا بسیار ساده و سرراست است: نرم طول یا اندازه‌ی بردار است؛ بااین‌حال مفهوم نُرم (Norm) در حوزه‌ی یادگیری ماشین و یادگیری عمیق اهمیت زیادی دارد؛ زیرا از آن برای ارزیابی خطای مدل استفاده می‌شود. از نُرم برای محاسبه‌ی خطای میان خروجی یک شبکه‌ی عصبی و خروجی مورد انتظار (مقدار یا برچسب واقعی) استفاده می‌شود. نُرم تابعی است که یک بردار را به یک مقدار مثبت نگاشت می‌کند؛ این یعنی نُرم همواره یک مقدار مثبت است. در این مقاله روش‌های مختلف محاسبه‌ی نُرم (Norm) یا اندازه‌ی بردار را معرفی می‌کنیم که به‌عنوان نُرم بردار (Vector Norm) هم شناخته می‌شود.
نُرم (Norm) چیست؟
برای پاسخ به پرسش نُرم (Norm) چیست بیایید با این گزاره شروع کنیم: نُرم یا Norm تابعی است با این ویژگی‌ها:
- نُرم‌های بردار مقادیری غیرمنفی هستند. اگر به نُرم به‌عنوان طول یک بردار فکر کنید، به‌راحتی متوجه می‌شوید که چرا نمی‌توانند منفی باشند.
- نُرم‌های بردار فقط در صورتی صفر خواهند بود که خود بردار صفر باشد.
- نُرم‌ها از نامساوی مثلثی پیروی می‌کنند؛ به‌این معنا که نُرم مجموع تعدادی بردار، کمتر یا مساوی مجموع نرم‌های این بردارهاست.
- زمانی که یک بردار بلندتر می‌شود یا به‌اصطلاح کشیده می‌شود، ضریب کشیدگی در مقدار نُرم آن ضرب می‌شود.
در ادامه با انواع مختلف نُرم که با استفاده از آن می‌توانیم طول یک بردار را محاسبه کنیم آشنا خواهیم شد.
نُرم L0
نُرم L0، طبق شرایطی که در به آن اشاره شد، درواقع یک نُرم نیست. این نُرم به تعداد کل عناصر غیرصفر در یک بردار اشاره می‌کند؛ برای مثال، نُرم L0 بردارهای (0،0) و (0،2) برابر با 1 است؛ زیرا فقط یک عنصر غیر صفر در آن‌ها وجود دارد.
یک مثال عملی خوب از نُرم L0 داشتن دو بردار نام کاربری و رمز عبور است. درصورتی‌که نُرم L0 بردارها برابر با 0 باشد، ورود به سیستم موفقیت‌آمیز است؛ در غیر این صورت، اگر نُرم L0 برابر با ۱ باشد، به‌این معنی است که یا نام کاربری یا رمز عبور نادرست است. اگر هم نُرم L0 برابر با ۲ باشد، یعنی نام کاربری و رمز عبور هر دو نادرست است.
نُرم L1
این نُرم به‌عنوان فاصله‌ی منهتن یا نُرم Taxicab نیز شناخته می‌شود. نُرم L1 مجموع اندازهٔ بردارها در یک فضاست. این نُرم معمولی‌ترین روش اندازه‌گیری فاصله‌ی میان بردارهاست که در آن جمع فاصله‌ی مطلق مؤلفه‌های بردار محاسبه می‌شود.
برای مثال، بردار X = [3،4] را که در شکل ۱ داریم، در نظر بگیرید:
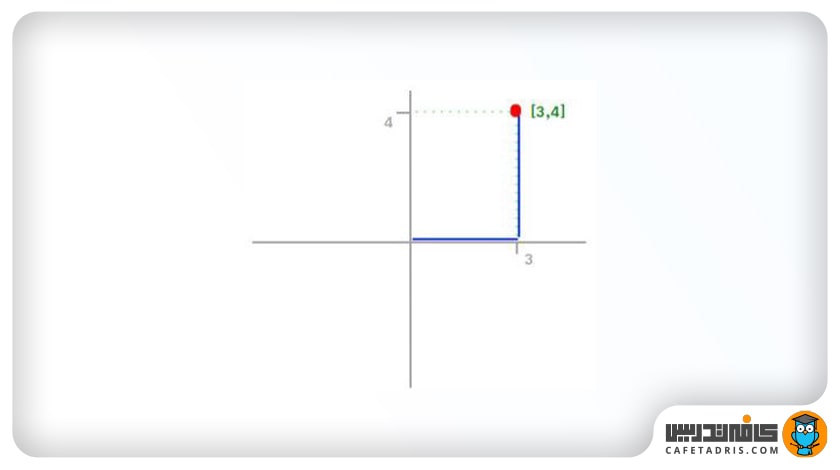
نُرم L1 به‌این شکل محاسبه می‌شود:
همان‌طور که در نمودار شکل ۱ مشاهده می‌کنید، نُرم L1 مسافتی است که باید میان مبدأ (۰/۰) تا مقصد (۳،۴) طی شود، دقیقاً مشابه نحوه‌ی حرکت تاکسی که در خیابان‌های شهر حرکت می‌کند تا به مقصد برسد.
نُرم L2
نُرم L2 با نام فاصله‌ی اقلیدوسی هم شناخته می‌شود و از معروف‌ترین نُرم‌هاست. این نُرم کوتاه‌ترین فاصله‌ی میان دو نقطه است.
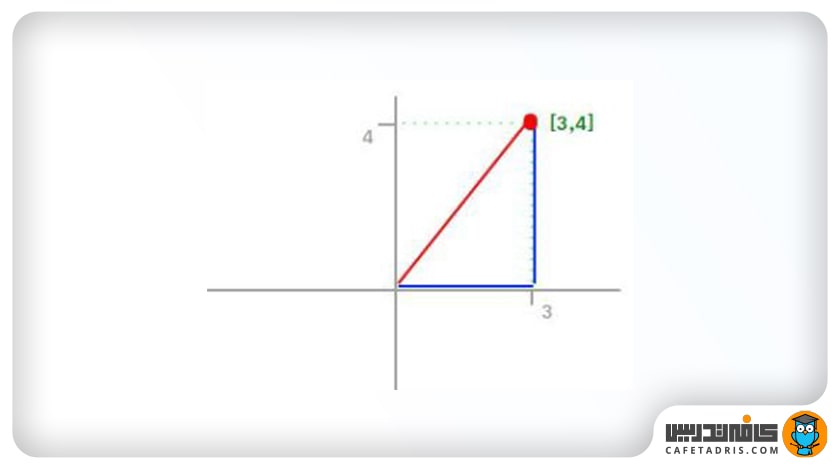
با درنظرگرفتن بردار مثال قبل، نُرم L2 به‌این شکل محاسبه می‌شود:
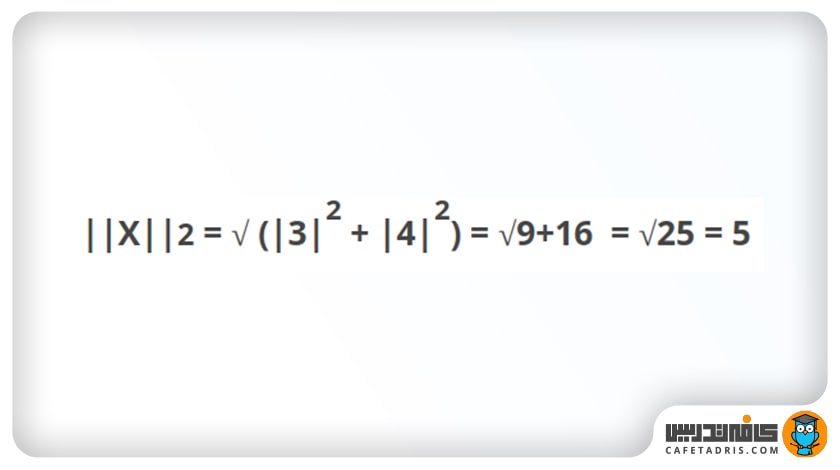
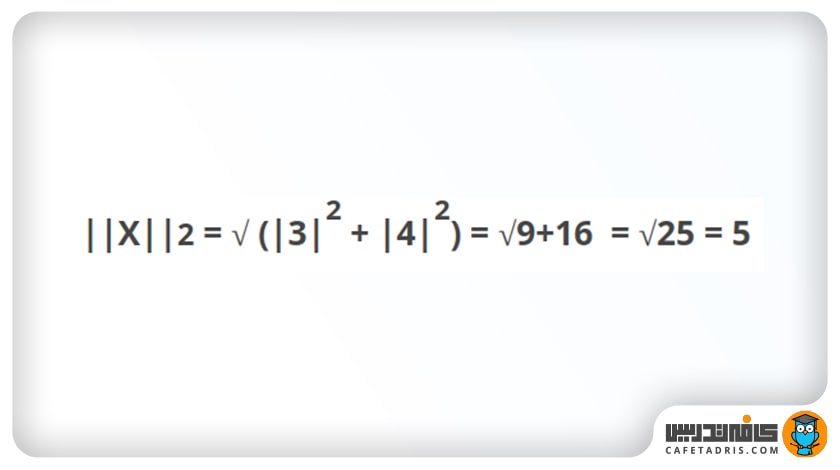
همان‌طور که در نمودار شکل ۲ مشاهده می‌کنید، نُرم L2 سرراست‌ترین مسیر میان دو نقطه است.
نُرم L-infinity
این نُرم بیشترین مقدار را در میان هر مؤلفه‌ی بردار برمی‌گرداند.
برای مثال، با داشتن بردار [6-، 4، 2] = X، نُرم L-infinity برابر با ۶ است. در نُرم L-infinity، فقط بزرگ‌ترین مؤلفه تأثیر می‌گذارد؛ بنابراین برای مثال، اگر بردار شما نشان‌دهنده‌ی هزینه‌ی ساخت یک ساختمان باشد، با به‌حداقل‌رساندن نُرم L-infinity، هزینه‌ی گران‌ترین ساختمان را کاهش می‌دهیم.
حرف آخر
در این مطلب به این پرسش پاسخ دادیم که نُرم (Norm) چیست و با مفهوم آن آشنا شدیم؛ همین‌طور متوجه شدیم ویژگی‌های یک نُرم چیست و درنهایت با انواع مختلف آن آشنا شدیم. نُرم مفهوم مهمی در یادگیری ماشین و یادگیری عمیق است و در محاسبه‌ی خطای مدل استفاده می‌شود.
برای آشنایی بیشتر با یادگیری ماشین و کاربردهای آن این مطلب را مطالعه کنید:
یادگیری ماشین (Machine Learning) چیست و چگونه کار می‌کند؟
یادگیری دیتا ساینس و ماشین لرنینگ با کلاس‌های آنلاین آموزش علم داده کافه‌تدریس
اگر به یادگیری علم داده و دانش یادگیری ماشین و یادگیری عمیق علاقه دارید، پیشنهاد ما شرکت در کلاس‌های آنلاین دیتا ساینس کافه‌تدریس است.
کلاس‌های جامع آنلاین آموزش علم داده کافه‌تدریس به شما امکان می‌دهد از هر نقطه‌ی جغرافیایی به به‌روزترین و کامل‌ترین آموزش دیتا ساینس و ماشین لرنینگ و دیپ لرنینگ دسترسی داشته باشید.
این کلاس‌ها به‌صورت کاملاً تعاملی و پویا و کارگاهی برگزار می‌شود و مبنای آن کار روی پروژه‌های واقعی دنیای علم داده است.
شما با شرکت در کلاس‌های آنلاین آموزش علم داده کافه‌تدریس صفر تا صد دیتا ساینس را در کوتاه‌ترین زمان ممکن یاد خواهید گرفت.
برای آشنایی بیشتر با کلاس‌های آنلاین آموزش دیتا ساینس کافه‌تدریس و مشاوره‌ی رایگان برای شروع یادگیری علم داده روی این لینک کلیک کنید: