پس انتشار در شبکه عصبی یا عملیات انتشار رو به عقب یا بهانگلیسی Backpropagation روش یادگیری شبکههای عصبی است. در این مطلب، با استفاده از مثالی با دادههای عددی، بهسادهترین حالت ممکن عملیات پس انتشار در شبکه عصبی را توضیح دادهایم.
- 1. ساختار شبکههای عصبی مصنوعی (Artificial Neural Networks / ANN)
- 2. پس انتشار در شبکه عصبی یا عملیات انتشار روبهعقب
- 3. بهحداقلرسیدن خطای شبکه چطور عملی میشود؟
- 4. فرایند انتشار رو به جلو (Forward Pass / Forward Propagation)
- 5. محاسبه خطای خروجی شبکه
- 6. فرایند پس انتشار در شبکه عصبی یا عملیات انتشار رو به عقب (Backpropagation)
- 7. یادگیری دیتا ساینس و ماشین لرنینگ با کلاسهای آنلاین آموزش علم داده کافهتدریس
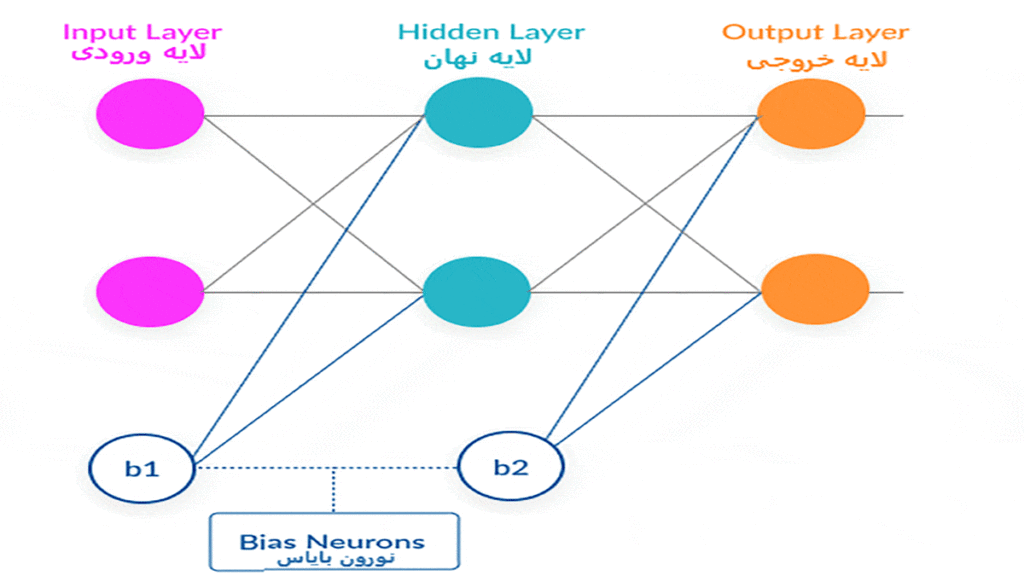

ساختار شبکههای عصبی مصنوعی (Artificial Neural Networks / ANN)
شبکههای عصبی مصنوعی (Artificial Neural Networks / ANN) سه نوع لایه از نورونها دارند. اولین لایه لایهی ورودی (Input Layer) است. داده ازطریق این لایه به شبکه وارد میشود. لایهی آخر، لایهی خروجی (Output Layer) است که دادهها بعد از عبور از تمامی لایههای شبکه به آن وارد میشود و سپس از شبکه خارج میشوند. میان دو لایهی ورودی و خروجی لایه یا لایههایی وجود دارد بهنام لایهٔ نهان (Hidden Layer) که داده از از آنها عبور میکنند.
تمام این لایهها تعداد متفاوتی نورون دارند. شبکههای عصبی از همین نورونهای متصلبههم تشکیل شدهاند. علاوه بر دادههای ورودی، وزنهایی برای هر یک از این اتصالات نورونها وجود دارد که درواقع نشاندهندهی تأثیر دادههای ورودی روی خروجی است؛ بهعبارت دیگر، این وزنها میزان قدرت هر یک از نورونها را مشخص میکنند. این وزنها در ابتدا مقادیری بهصورت رندوم یا تصادفی دارند. وقتی صحبت از آموزش شبکههای عصبی میکنیم، منظور فرایند بهروزرسانی همین وزنهاست تا شبکه بتواند خروجی قابل قبولی را با توجه به دادههای ورودی ارائه دهد.
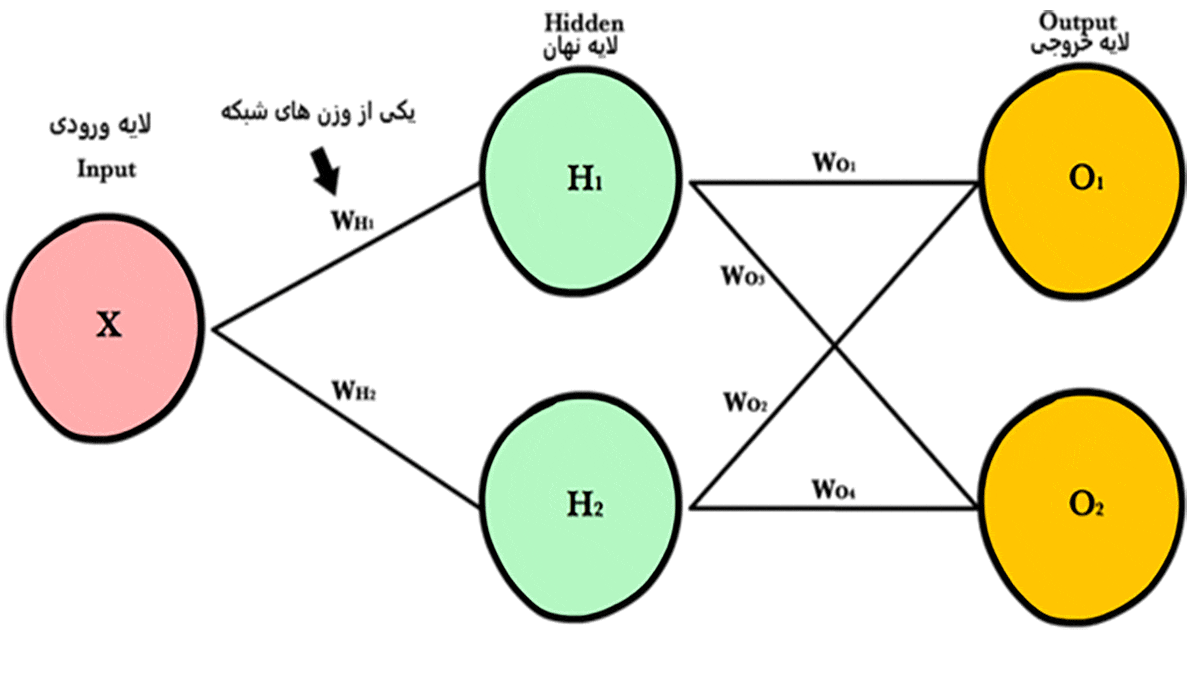

فرایند بهروزرسانی وزنها عملیات پس انتشار یا انتشار رو به عقب (Backpropagation) نامیده میشود. در ادامه با هم چگونگی این عملیات را بررسی میکنیم.
پیشنهاد میکنیم با شبکه عصبی LSTM بیشتر آشنا شوید.
پس انتشار در شبکه عصبی یا عملیات انتشار روبهعقب
همانطور که پیشتر متوجه شدیم، فرایند آموزش شبکه بهمعنای بهروزرسانی وزنهای شبکه است. این بهروزرسانی فرایند پس انتشار در شبکه عصبی یا انتشار رو به عقب نامیده میشود که هدف آن یادگیری وزنها و ماکزیممکردن مقدار دقت (Accuracy) خروجی است. برای ماکزیممکردن مقدار دقت شبکه لازم است با تغییردادن وزنها مقدار خطا (Error) را به حداقل برسانیم. میتوانیم تأثیر وزنهای شبکه روی خطا را در شکل ۳ ببینیم.
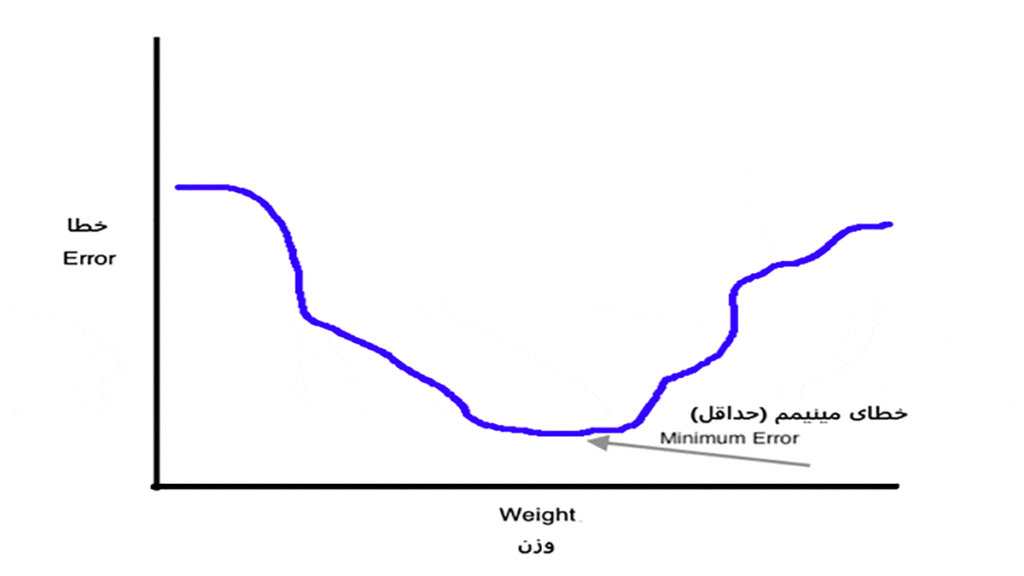

هدف در پس انتشار در شبکه عصبی یا عملیات انتشار رو به عقب این است که وزنها را بهقدری تغییر دهیم تا به حداقل خطای ممکن برسیم.
بهحداقلرسیدن خطای شبکه چطور عملی میشود؟
برای درک این مسئله برای مثال در نظر بگیریم که یک شبکهی عصبی مانند شکل ۴ داریم. در ابتدا میخواهیم یک بار عملیات انتشار رو به جلو (Forward Propagation / Forward Pass) را انجام دهیم و خطای کل را محاسبه کنیم. سپس فرایند پس انتشار یا عملیات انتشار رو به عقب را انجام میدهیم. برای این کار مقدار وزنها و ورودی را خودمان تعیین میکنیم و همچنین مقدار خروجی مدنظر را هم مشخص میکنیم (۰.۹۹) (این مقادیر بهدلخواه است و فقط برای درک نحوه کار فرایند پس انتشار یا عملیات انتشار روبهعقب انتخاب شده است).
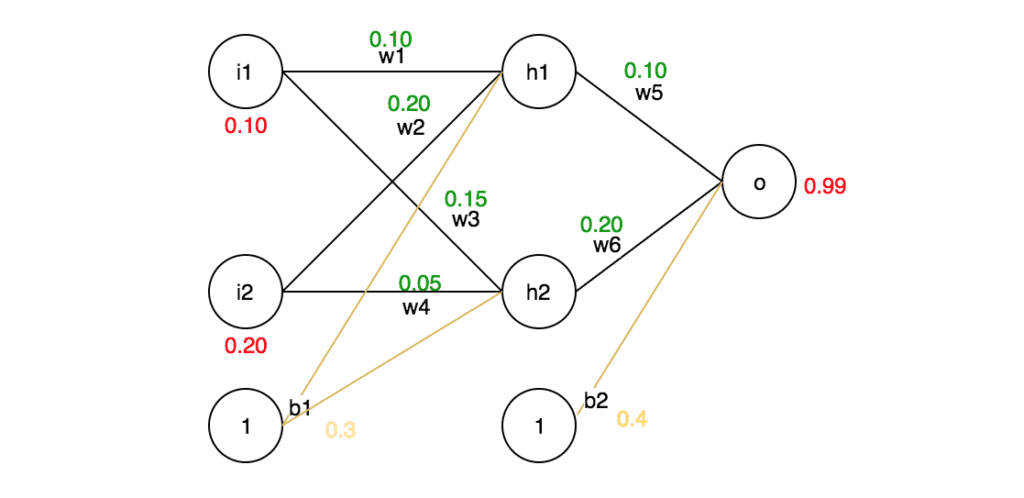

فرایند انتشار رو به جلو (Forward Pass / Forward Propagation)
در فرایند انتشار رو به جلو مقدار هر ورودی در وزن متناظرش ضرب میشود؛ سپس نتیجهی این ضربها با هم و با مقدار بایاس جمع میشوند. بعد از آن خروجی این جمع به یک تابع فعالساز وارد میشود که فرض میکنیم در مثال ما تابع فعالساز مورداستفاده سیگموید (Sigmoid) است.
حال میخواهیم در مثال گفتهشده این عملیات را برای نورونهای لایه نهان بهترتیب برای نورون h1 و h2 انجام دهیم:
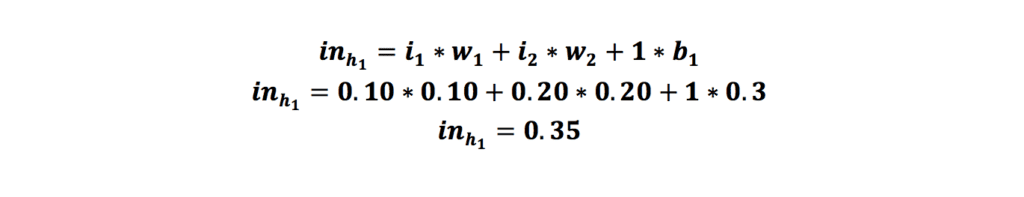
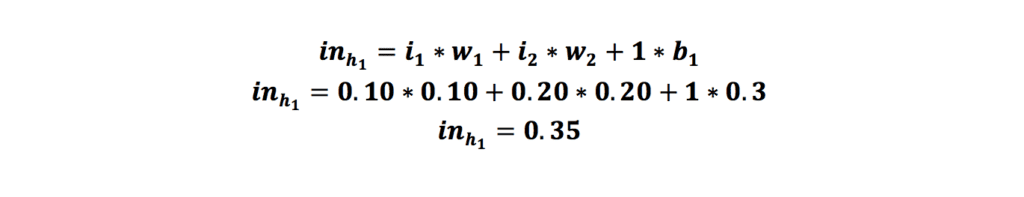
بعد از محاسبهی مجموع ضرب ورودیها با وزن منتناظرشان بههمراه مقدار بایاس، خروجی را به تابع سیگموید میکنیم و این خروحی را به دست میآوریم:
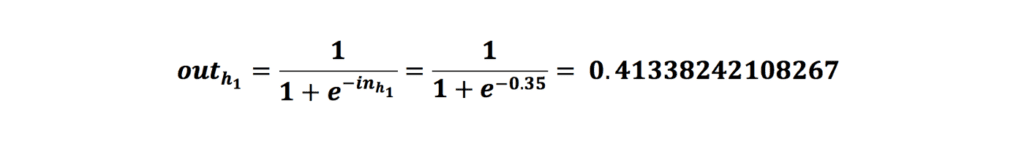
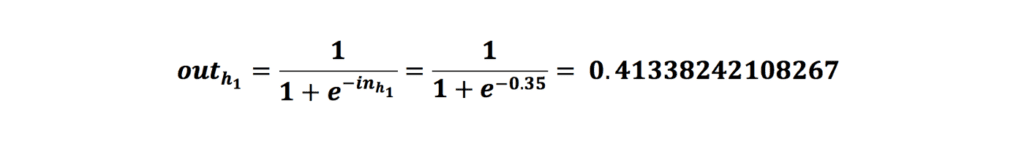
همین مرحلهها را برای نورون h2 در لایه نهان انجام میدهیم:
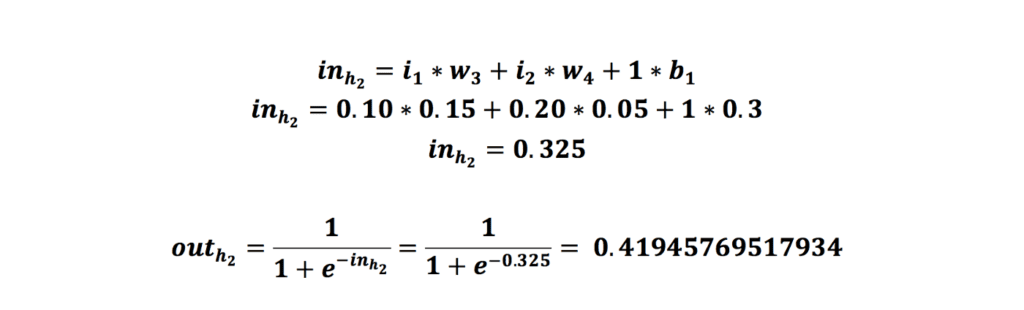
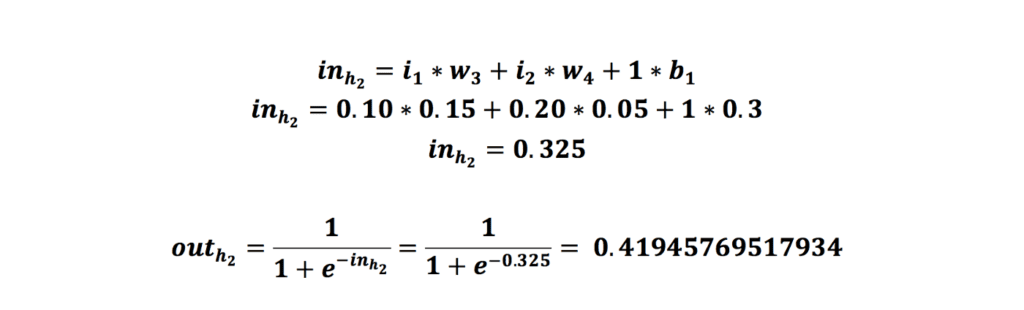
در مرحلهی آخر از فرایند انتشار رو به جلو باید همین مقدار را برای نورون لایهی خروجی هم انجام دهیم.
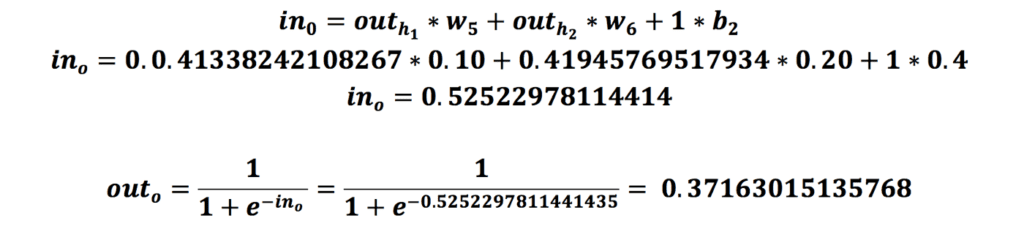
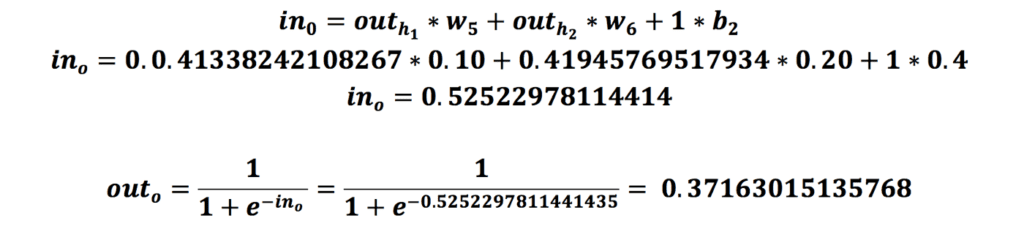
پیشنهاد میکنیم با توابع فعالساز بیشتر آشنا شوید.
محاسبه خطای خروجی شبکه
تا الان فرایند انتشار رو به جلو و محاسبات لازم انجام شد. در حال حاضر ما خروجی شبکه را به دست آوردیم که برابر با 0.37163015135768 است. همانطور که در ابتدا به آن اشاره شد، خروجی مدنظر ما ۰.۹۹ است و خروجی که بهدستآمده با خروجی مدنظر فاصله زیادی دارد. برای اینکه میزان خطا (فاصلهی خروجی بهدستآمده با خروجی مدنظر) را کاهش دهیم باید مقدار وزنهای شبکه را تغییر دهیم تا زمانی که به خروجی دلخواه برسیم. توابع مختلفی برای محاسبهی خطای شبکه وجود دارد که به آنها تابع زیان (Loss Function) گفته میشود. در اینجا ما از تابع خطای میانگین مربعات (MSE / Mean Squared Error) استفاده میکنیم که بهاین صورت است:
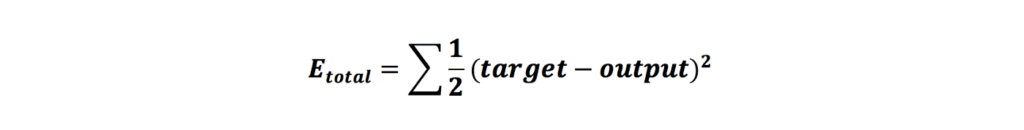
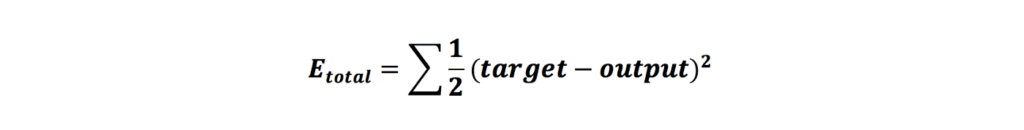
حال که فرمول تابع زیان را داریم، میتوانیم بهراحتی خطای شبکه را محاسبه کنیم:
پس از محاسبهی خطای شبکه، زمان انجامدادن فرایند پس انتشار یا انتشار رو به عقب (Backpropagation) است.
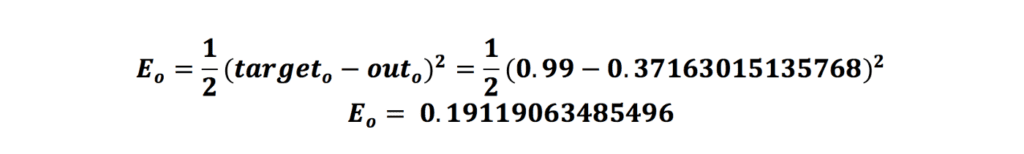
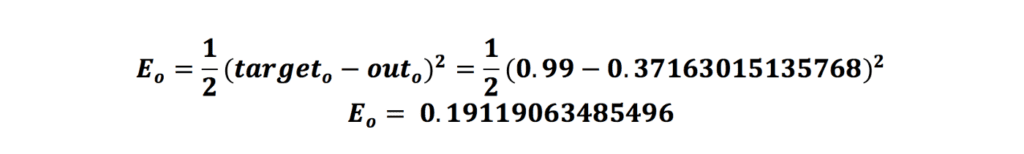
پیشنهاد میکنیم با شبکه عصبی واحد بازگشتی گیتی آشنا شوید.
فرایند پس انتشار در شبکه عصبی یا عملیات انتشار رو به عقب (Backpropagation)
حال زمان آن رسیده است که به عقب حرکت کنیم و وزنهای شبکه را بهروزرسانی کنیم تا به خروجی مدنظر برسیم.
از لایهی آخر شروع میکنیم. فرض کنیم که میخواهیم وزن w5 را بهروزرسانی کنیم. باید ابتدا تأثیر وزن w5 را روی خطای کل، یعنی همان خطایی که در مرحلهی قبل به دست آوردیم، محاسبه کنیم که همان مشتق (Derivative) خطای کل نسبت به وزن w5 یا گرادیان است:


حل گامبهگام معادله
حال این معادله را بهصورت گامبهگام محاسبه میکنیم:
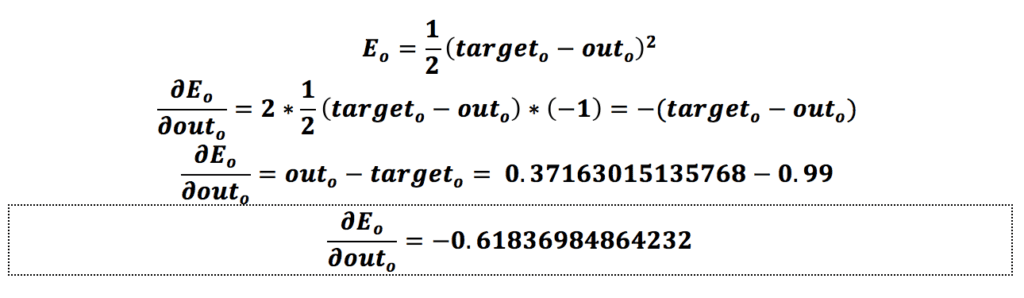
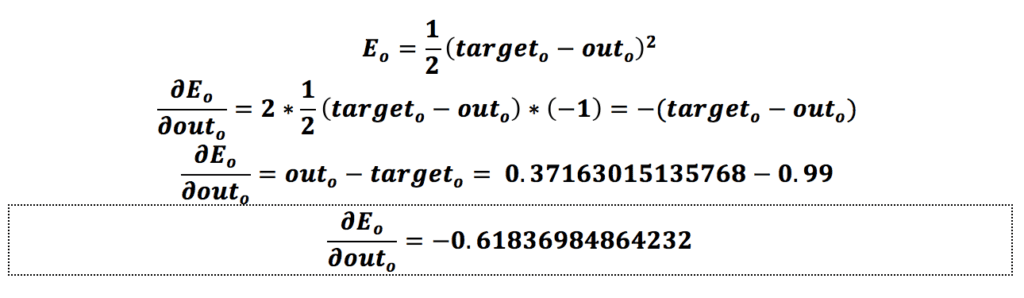
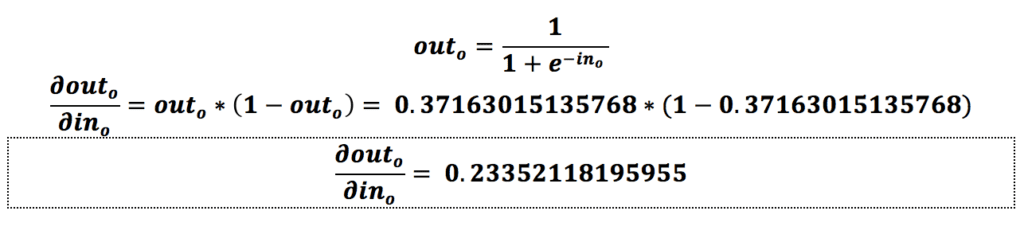
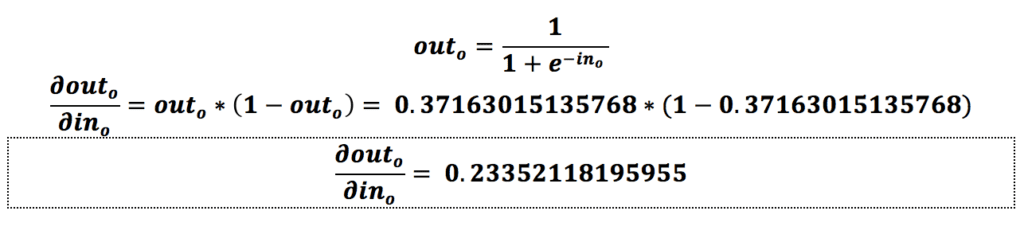
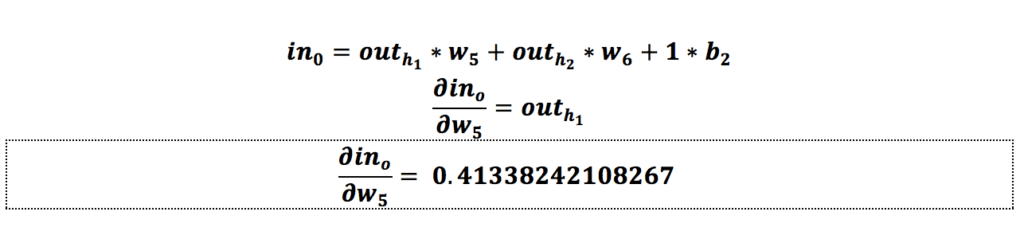
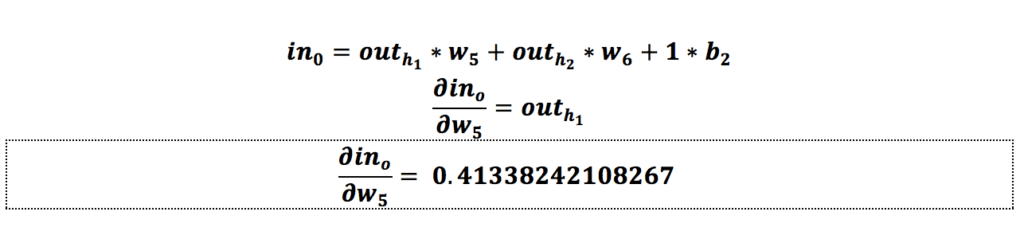


همانطور که مشاهده میکنیم، میزان تأثیر وزن w5 روی خطای شبکه برابر با 0.059693437674795- است؛ درواقع تأثیر وزن w5 میزان خطای شبکه با این ورودیها را کاهش میدهد.
حال لازم است که وزن w5 را بهروزرسانی کنیم. برای بهروزرسانی باید مقدار گرادیان (مشتق خطای کل نسبت به w5) را از مقدار وزن اولیه w5 کم کنیم؛ البته در اینجا مقدار نرخ یادگیری (Learning Rate) را هم داریم که باید در مقدار گرادیان ضرب شود که کاری که انجام میدهد مقدار مقادیر را بین ۰ و ۱ قرار میدهد. ما در اینجا مقدار نرخ یادگیری را ۰.۴ در نظر میگیریم؛ پس محاسبه مقدار جدید برای وزن w5 بهاین شکل انجام میشود:


حال تمامی مراحلی که برای وزن w5 انجام دادیم برای وزن w6 انجام میدهیم:
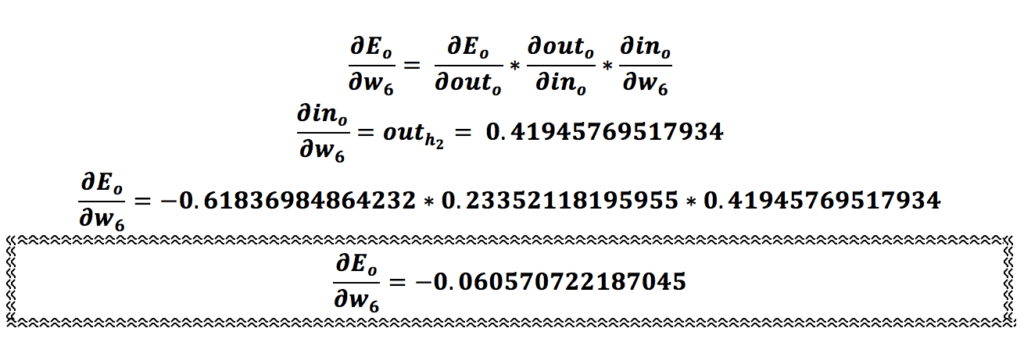
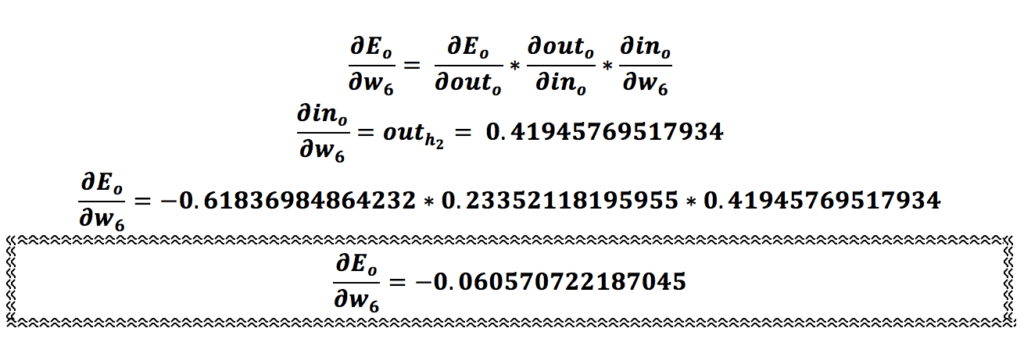
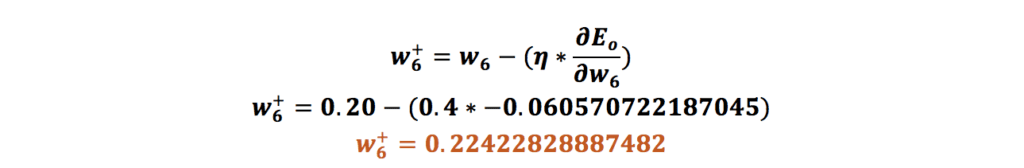
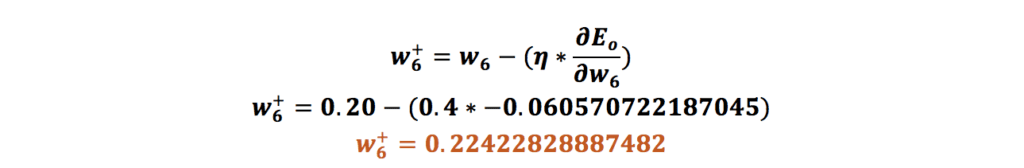
بهروزرسانی
وقتی مقدار جدید وزن w6 را به دست آوردیم باید به سراغ وزنهای میان لایههای نهان و ورودی، یعنی w1,w2,w3 و w4، برویم و آنها را هم بهروزرسانی کنیم.
در اینجا باید در نظر بگیریم که در بهروزرسانی این وزنها از مقدار اولیهی وزنهای w5 و w6 استفاده میکنیم، نه مقدار بهروزرسانیشده.
زمانی که تمامی وزنهای شبکه بهروزرسانی شوند و برای بار دوم عملیات انتشار رو به جلو را انجام میدهیم از مقادیر بهروزرسانیشده وزنها استفاده میکنیم.
برای بهروزرسانی این وزنها باید مراحل قبلی را بار دیگر طی کنیم؛ یعنی ابتدا مقدار گرادیان یا همان مشتق خطای کل نسبت به هر یک از وزنها را به دست آوریم.
ابتدا از وزن w1 شروع میکنیم:
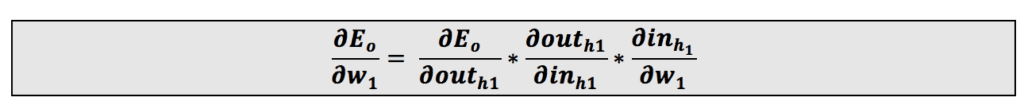
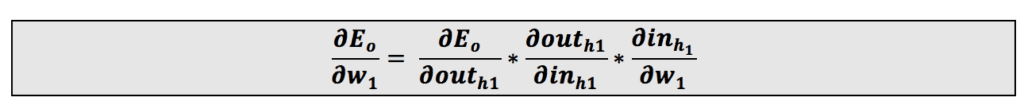
این معادله را میتوان بهاین شکل نوشت:
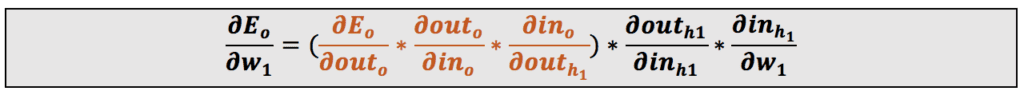
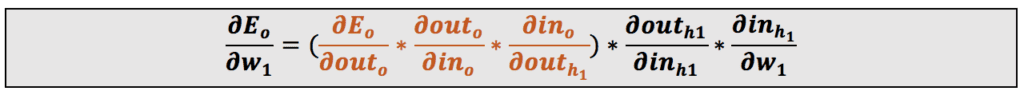
این معادله را گامبهگام انجام میدهیم:
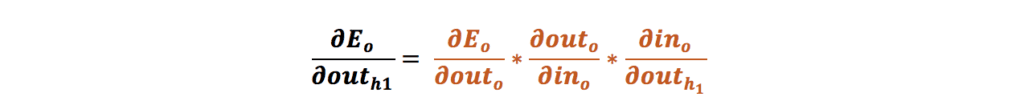
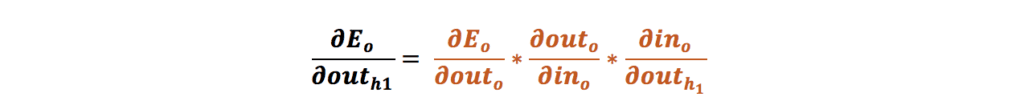
ما قبلاً هنگام محاسبهی مقادیر جدید وزنهای w5 و w6 مقدار گرادیان نسبت به خروجی و مقدار گرادیان نسبت به ورودی را محاسبه کردهایم. حالا فقط لازم است مقدار گرادیان نسبت به w1 را به دست بیاوریم:
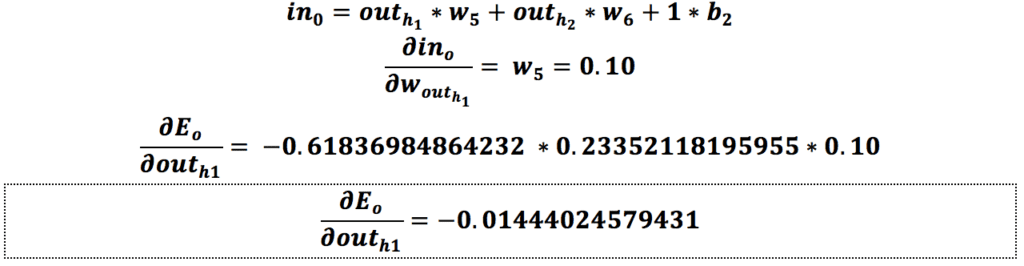
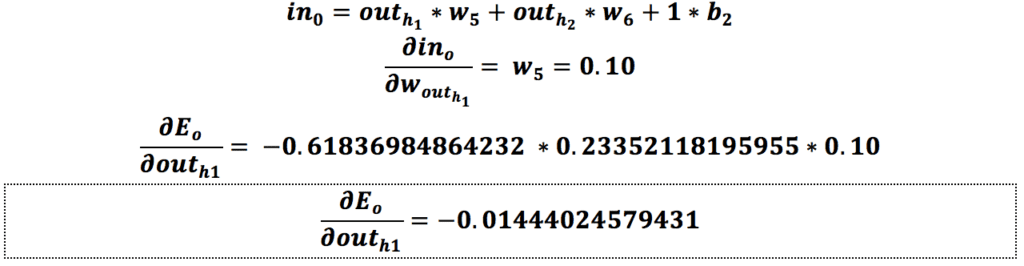
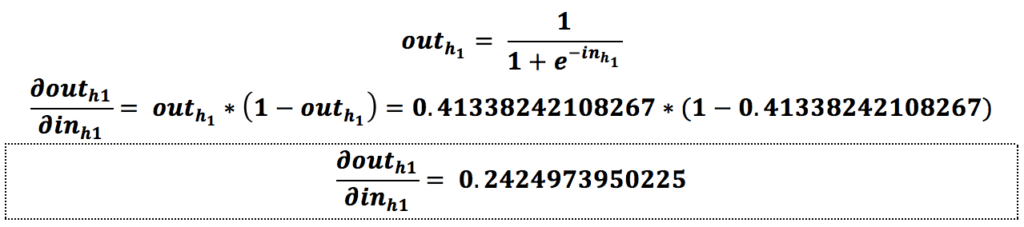
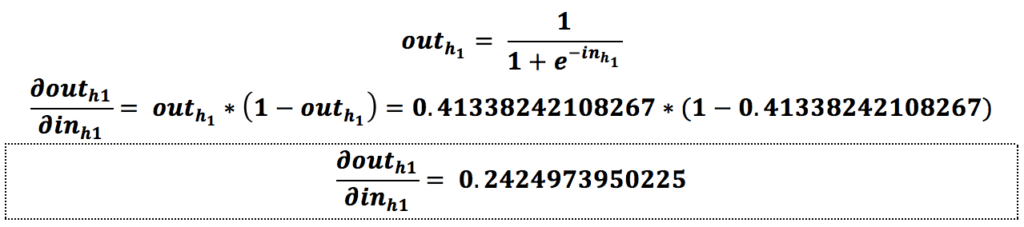
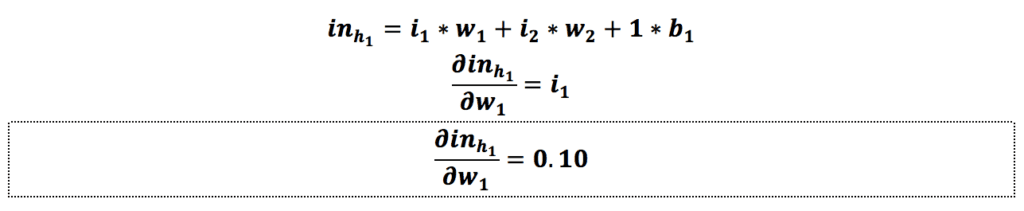
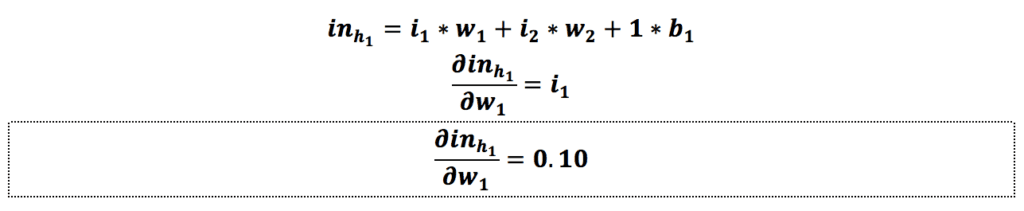


حالا که مقدار گرادیان نسبت به w1 را به دست آوردیم فقط لازم است مقدار آن را بهروزرسانی کنیم.
همین محاسبه را برای وزنهای w2، w3 و w4 هم انجام میدهیم:
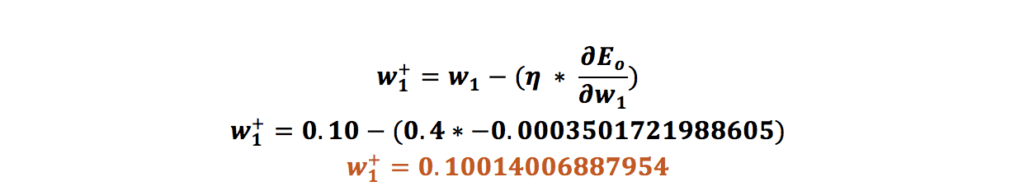
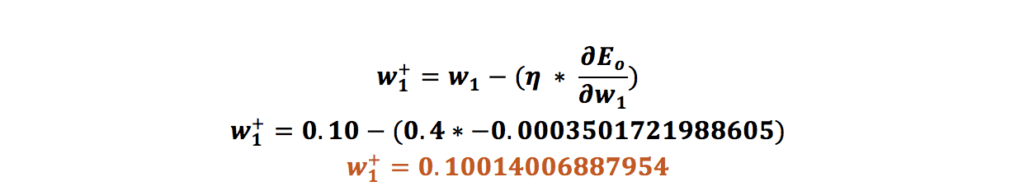
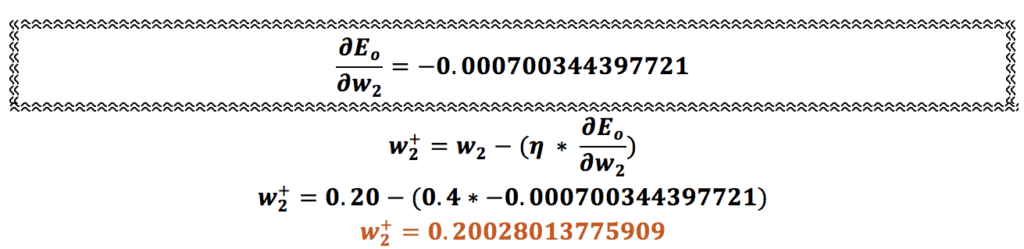
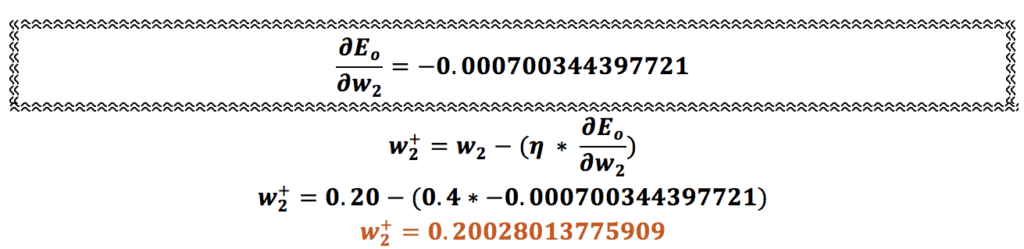
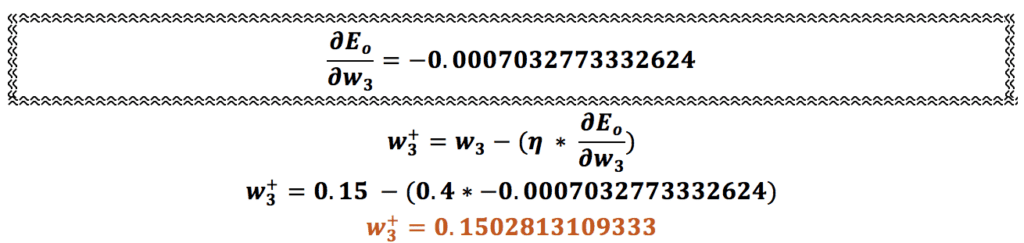
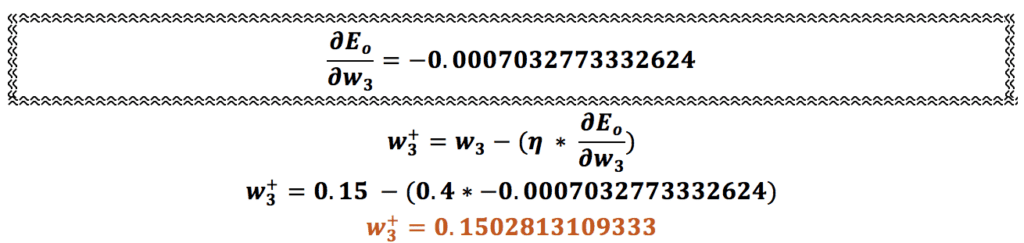
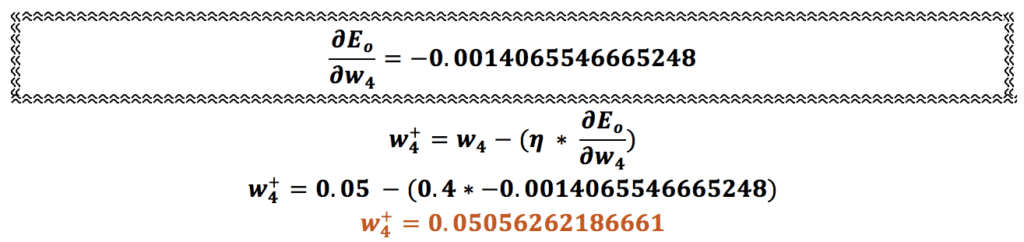
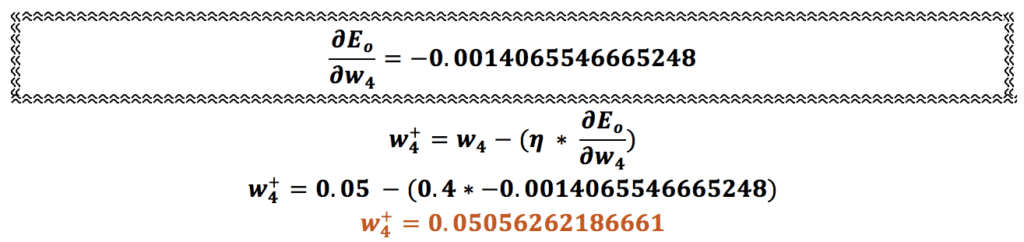
اتمام فرایند پس انتشار در شبکه عصبی یا عملیات انتشار روبه عقب
فرایند پس انتشار در شبکه عصبی یا عملیات انتشار روبهعقب کامل شد و ما تمامی وزنهای شبکه را بهروزرسانی کردیم. حال اگر دوباره عملیات انتشار رو به جلو را با وزنهای جدید تکرار کنیم خروجی ما این بار 0.64623980051852 خواهد بود که در مقایسه با خروجی که با وزنهای رندوم داشتیم، بهبود چشمگیری کرده است. اگر چندین بار این مراحل تکرار شود، قطعاً مدل خروجی بهتری را درنهایت به ما ارائه میکند که به خروجی موردانتظار (۰.۹۹) نزدیک باشد.
یادگیری دیتا ساینس و ماشین لرنینگ با کلاسهای آنلاین آموزش علم داده کافهتدریس
اگر دوست دارید دانش ماشین لرنینگ و دیتا ساینس را بیاموزید، کلاسهای آنلاین آموزش علم داده کافهتدریس به شما کمک میکند از هر نقطهی جغرافیایی به بهروزترین و جامعترین آموزش دیتا ساینس و ماشین لرنینگ دسترسی داشته باشید.
کلاسهای آنلاین آموزش علم داده کافهتدریس در دورههای مقدماتی و پیشرفته برگزار میشود و شکل برگزاری آن کاملاً پویا و تعاملی است. مبنای این کلاسهای آنلاین هم کار روی پروژههای واقعی دیتا ساینس است.
برای آشنایی بیشتر با کلاسهای آنلاین آموزش علم داده کافهتدریس و مشاورهی رایگان برای شروع یادگیری دیتا ساینس و ماشین لرنینگ و مسیر شغلی آن روی این لینک کلیک کنید:



بسیار عالی بود
سلام و عرض ادب،
خوشحالیم که مطلب براتون مفید بوده و نظرتون رو با ما به اشتراک گذاشتین.
خیلی واضح و خوب بود. خدا قوت
ممنون از توجه شما
بسیااااار عالی
واقعا خسته نباشید
ممنون از توجه شما
خیلی مفید بود ممنون از زحمات شما
ادامه بدید و موفق باشید
خوشحالیم که براتون مفید بوده و از نظر مثبتتون متشکرم.
واقعا خسته نباشین
بهترین بلاگ آموزشی با اختلاف
ممنون از شما دوست عزیز.