رگرسیون لجستیک (Logistic Regression) یکی از الگوریتمهای یادگیری ماشین است. این الگوریتم برای مسائل طبقهبندی (Classification) استفاده میشود که در آن متغیر وابستهی گسسته (Categorical) مطرح میشود.
- 1. یادگیری ماشین چیست؟
- 2. طبقهبندی یا Classification چیست؟
- 3. رگرسیون لجستیک (Logistic Regression) چیست؟
- 4. چرا رگرسیون خطی نه؟
- 5. تابع هزینه (Cost Function)
- 6. گرادیان نزولی (Gradient Descent)
- 7. قسمتی از جزوه کلاس برای آموزش Logistic Regression
- 8. Logistic Regression در پایتون
- 9. خلاصهی مطالب دربارهی رگرسیون لجستیک (Logistic Regression)
قبل از بررسی رگرسیون لجستیک، بهتر است کمی با یادگیری ماشین و طبقهبندی آشنا شویم.
یادگیری ماشین چیست؟
یادگیری ماشین زیرمجموعهای از هوش مصنوعی است که شامل توسعه الگوریتمها و مدلهایی است که رایانهها را قادر میسازد از دادهها بدون برنامهریزی صریح یاد بگیرند. الگوریتمهای یادگیری ماشین برای تشخیص الگوها و روابط درون دادهها و استفاده از این الگوها برای پیشبینی یا تصمیمگیری درباره دادههای جدید طراحی شدهاند. یادگیری ماشین در سالهای اخیر به دلیل در دسترس بودن حجم زیادی از دادهها و توسعه منابع محاسباتی قدرتمندتر به طور فزایندهای محبوب شده است.
انواع مختلفی از الگوریتمهای یادگیری ماشین وجود دارد، از جمله یادگیری تحت نظارت، یادگیری بدون نظارت و یادگیری تقویتی. یادگیری تحت نظارت شامل استفاده از دادههای برچسب دار برای آموزش مدل است، در حالی که یادگیری بدون نظارت شامل یافتن الگوها در دادههای بدون برچسب است. یادگیری تقویتی شامل استفاده از یک سیستم پاداش برای تشویق مدل به یادگیری از تجربیاتش است. یادگیری ماشین طیف گستردهای از کاربردها، از تشخیص تصویر و گفتار گرفته تا تشخیص تقلب را دارد و به طور فزایندهای در صنایعی مانند مراقبتهای بهداشتی، مالی و حملونقل استفاده میشود.
طبقهبندی یا Classification چیست؟
طبقهبندی (Classification) نوعی یادگیری تحت نظارت در یادگیری ماشین است که شامل پیشبینی یک متغیر خروجی بر اساس متغیرهای ورودی است. در طبقهبندی، یک مدل بر روی یک مجموعه داده برچسب دار با مقادیر خروجی شناخته شده آموزش داده میشود و هدف استفاده از این مدل برای پیشبینی دقیق مقدار خروجی دادههای ورودی جدید است.
دادههای ورودی مورد استفاده برای آموزش مدل طبقهبندی معمولاً شامل ویژگیهایی هستند که با پیشبینی متغیر خروجی مرتبط هستند. به عنوان مثال، در یک سیستم تشخیص ایمیل اسپم، ویژگیها ممکن است شامل موضوع، آدرس فرستنده و محتوای ایمیل باشد. متغیر خروجی در این مورد یک طبقه بندی باینری است که نشان میدهد ایمیل اسپم است یا خیر.
انواع مختلفی از مدلهای طبقه بندی وجود دارد که میتوانند در یادگیری ماشین استفاده شوند، از جمله رگرسیون لجستیک، درخت تصمیم، جنگلهای تصادفی، ماشین بردار پشتیبان و شبکههای عصبی. انتخاب مدل به مشکل خاصی که قرار است حل شود و ویژگیهای دادهها بستگی دارد.
طبقهبندی کاربردهای گستردهای در زمینههای مختلف دارد، از جمله پردازش زبان طبیعی، تشخیص تصویر، تشخیص تقلب و تشخیص پزشکی. طبقهبندی یک تکنیک مهم و قدرتمند در یادگیری ماشین است که میتواند به خودکارسازی تصمیمگیری و بهبود کارایی و دقت بسیاری از فرآیندها کمک کند.
رگرسیون لجستیک (Logistic Regression) چیست؟
رگرسیون لجستیک یکی از الگوریتمهای طبقهبندی (Classification) است که برای اختصاص دادهها به مجموعهای از کلاسها استفاده میشود. برخی از نمونههای مسائل طبقهبندی عبارتاند از: طبقهبندی ایمیلها به دو دستهی ایمیلهای اسپم (Spam) یا غیراسپم (Not Spam) یا طبقهبندی معاملات آنلاین به دو دستهی کلاهبرداری یا غیرکلاهبرداری یا طبقهبندی تومورهای بدخیم یا خوشخیم.
همانطور که تا الان متوجه شدیم، بهطور کلی در رگرسیون لجستیک خروجی بهشکل صفر یا ۱ است؛ یعنی برای مثال، یا تورمور بدخیم است (1) یا خوش خیم (0).
زمانیکه تعداد کلاسهای خروجی 2 باشد، به آن طبقهبندی باینری (Binary Classification) گفته میشود؛ البته تعداد کلاسهای خروجی میتواند بیشتر هم باشد که در این صورت به آن طبقهبندی مالتی (Multi Classification) گفته میشود.
تا اینجا فهمیدیم که در رگرسیون لجستیک هدف در خروجی اختصاص دادهها به یکی از دو کلاس صفر یا ۱ است. درواقع در این تکنیک احتمال این را که داده به کدام کلاس متعلق است در خروجی خواهیم داشت. از آنجا که دربارهی احتمال صحبت میکنیم، پس قطعاً میدانیم خروجی ما باید بین صفر و ۱ باشد. حال لازم است ببینیم در اینجا ما به چه تابعی احتیاج داریم که بتواند دادهها را بهخوبی نمایش دهد و در کلاس درستی طبقهبندی کند.
چرا رگرسیون خطی نه؟
فرض کنید ما مجموعهدادهای داریم که اندازهی تومورها و این امر را که آیا بدخیم هستند یا نه نشان میدهد. اگر این دادهها را روی نمودار ببریم، از آنجا که مسئله طبقهبندی است، تمامی دادهها یا صفر هستند یا یک.
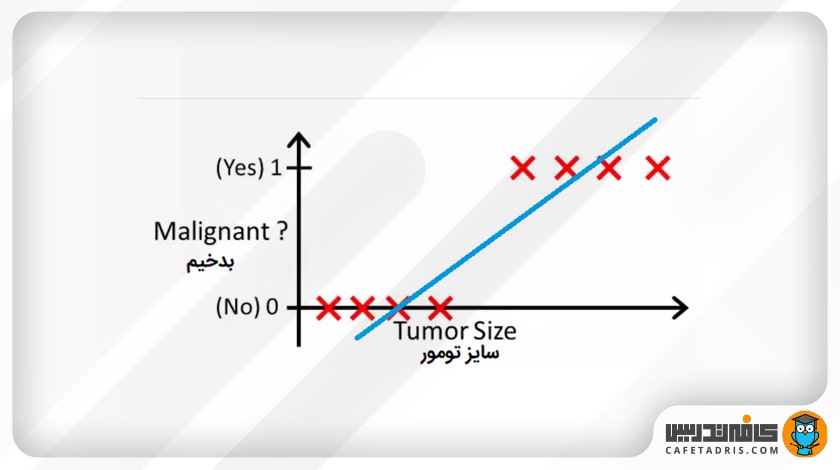

حال اگر از رگرسیون خطی استفاده کنیم، چنین خطی را که در نمودار بالا مشاهده میکنیم به ما میدهد. در اینجا میتوانیم با تعیین یک آستانه (Threshold) در محور x، دادهها را طوری تقسیم کنیم که همهی دادههای موجود در سمت راست آستانهی بدخیم (متعلق به کلاس ۱ یا همان مثبت) و در سمت چپ آن همهی دادههای موجود خوشخیم (متعلق به کلاس صفر یا همان منفی) هستند. در اینجا این آستانه ۰.۵ است.
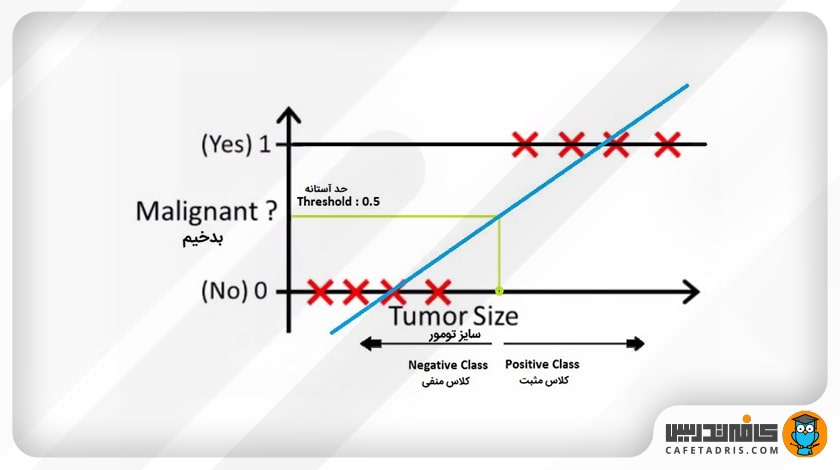

خب، تا اینجای کار رگرسیون خطی خوب جواب داده است و شاید فکر کنیم که اصلاً به رگرسیون لجستیک نیازی نداریم، اما اینطور نیست.
بیایید در نظر بگیریم یک دادهی پرت (Outlier) به این دادهها اضافه شود؛ در این صورت خطی که رگرسیون خطی به ما میدهد بهاین شکل خواهد بود:
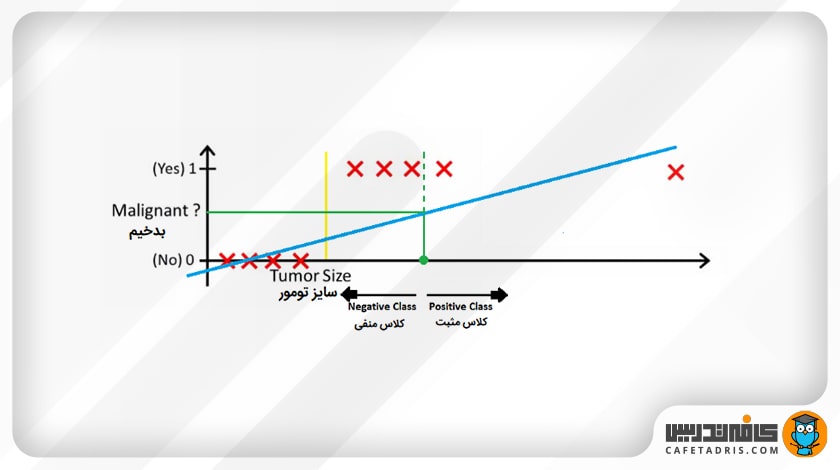

در اینجا اگر بازهی ۰.۵ را بار دیگر بررسی کنیم، میبینیم که دادهها بهدرستی تقسیم نمیشوند؛ خیلی از کلاسهای مثبت را بهاشتباه در دستهی کلاسهای منفی قرار میدهد. درواقع باید بگوییم بار اول رگرسیون خطی بهصورت اتفاقی دادهها را به درستی تقسیم کرد؛ پس بههمین دلیل، ما به رگرسیون لجستیک نیاز داریم.
اگر میخواهید درباره رگرسیون خطی بیشتر بدانید، مطلب رگرسیون خطی (Linear Regression) را حتماً مطالعه کنید.
چرا به رگرسیون لجستیک (Logistic Regression) نیاز داریم؟
همانطور که میدانیم، در رگرسیون خطی ما باید به بهترین معادلهی خطی میرسیدیم تا دادهها را بهدرستی نمایش دهد. این را در نظر بگیریم که در رگرسیون خطی معادلهی خطی میتواند هر مقداری داشته باشد، درحالیکه در طبقهبندی و رگرسیون لجستیک (Logistic Regression) مقادیری که در خروجی داریم احتمال تعلق داده به یکی از دو کلاس صفر یا ۱ است؛ بنابراین مقادیر باید میان صفر و ۱ باشد که این موضوع با معادله خطی امکانپذیر نیست.
پس ما به معادلهی دیگری احتیاج داریم که آن تابع سیگموید یا همان لجستیک (Sigmoid/ Logistic Function) است.
تابع سیگموید بهاین شکل است:
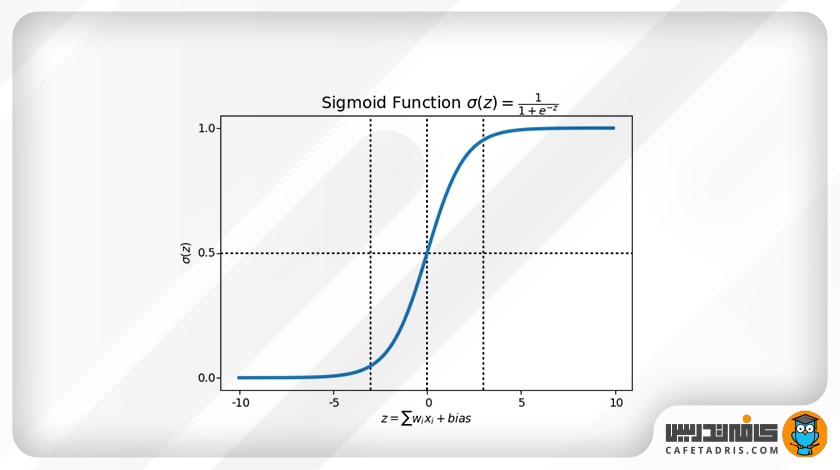

معادلهی خطیمان در رگرسیون خطی بهاین شکل بود:
Z = β₀ + β₁X
در رگسیون لجستیک معادلهی ما بهاین شکل خواهد بود:
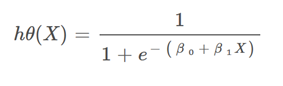
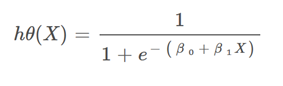
یعنی همان سیگموید معادلهی خطی خواهد بود که در رگرسیون خطی داشتیم.
قبل از اینکه ببینیم چطور پارامترهای این معادله را بهینه میکنیم، بیایید دربارهی مرز تصمیمگیری (Decision Boundary) صحبت کنیم.
مرز تصمیمگیری (Decision Boundary)
هنگامیکه ورودیها را از یک تابع پیشبینی عبور دهیم و در خروجی احتمالی میان صفر تا یک را داریم، همچنین انتظار داریم طبقهبندیکنندهی ما براساس احتمال، مجموعهای از کلاسها را به ما بدهد.
برای مثال، فرض کنید ۲ کلاس داریم؛ بیایید گربه و سگ (سگ کلاس ۱، گربه کلاس صفر) را در نظر بگیریم؛ حال یک آستانه در نظر میگیریم که هر دادهای بالای آن باشد متعلق به کلاس یک و هر دادهای زیر آن باشد متعلق به کلاس صفر در نظر گرفته شود.
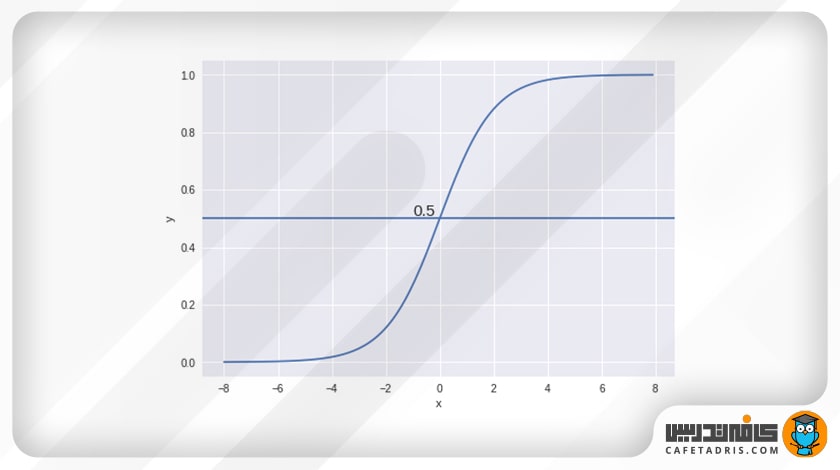

همانطور که در نمودار بالا نشان داده شده است، ما آستانه را ۰.۵ انتخاب کردهایم؛ اگر تابع پیشبینی مقدار ۰.۷ را بازگرداند، داده را بهعنوان کلاس یک (سگ) طبقهبندی میکنیم؛ اگر مقدار پیشبینی ۰.۲ باشد، داده را بهعنوان کلاس صفر (گربه) طبقهبندی میکنیم. درواقع مرز تصمیمگیری (Decision Boundary) به ما کمک میکند دو کلاس را از هم متمایز کنیم. این مرز تصمیمگیری را تابع لجستیک مشخص میکند.
حال لازم است بدانیم که پارامترهای تابع لجستیک یا همان سیگموید چطور به دست میآید.
تابع هزینه (Cost Function)
در رگرسیون لجستیک نیز، مانند رگرسیون خطی، ابتدا ما یک تابع با پارامترهای رندوم داریم که درنهایت با استفاده از تابع هزینه این پارامترها بهینه میشود تا در خروجی بهترین نتیجه را داشته باشیم؛ بهعبارت دیگر، دادهها بهدرستی طبقهبندی شوند.
تابع هزینه میزان خطای موجود را میان کلاسی که پیشبینی شده است و کلاسی که واقعاً داده به آن تعلق دارد مشخص میکند. در رگرسیون لجستیک این خطا را تابع هزینهی لگاریتمی بهاین شکل مشخص میکند:


که نمودار این دو بهاین شکل خواهد بود:
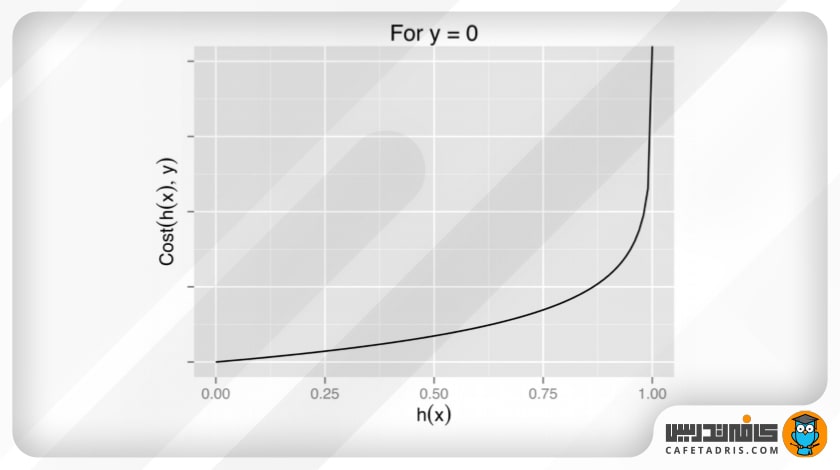

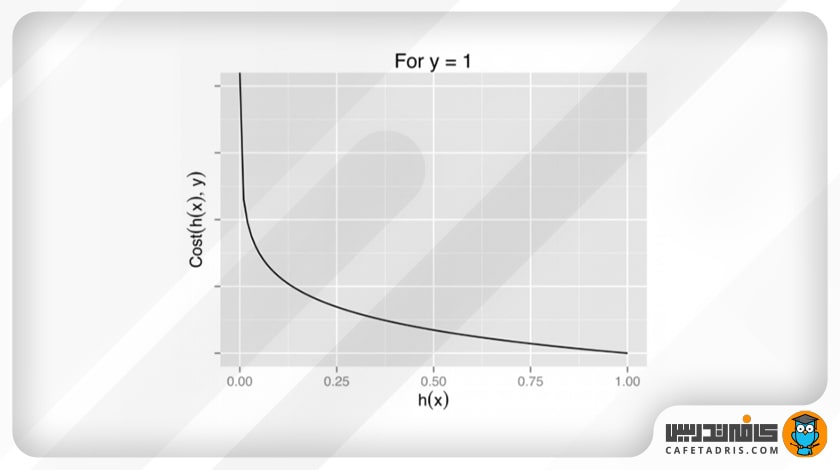

همانطور که میبینیم، اگر در نمودار y = 1 پیشبینی مدل ما این باشد که y = 0، یعنی داده را به کلاس اشتباه طبقهبندی کند، مقدار هزینه (Cost) بهسمت بینهایت میرود. در نمودار y = 0 هم، درصورتیکه پیشبینی مدل ما y = 1 باشد، بازهم مقدار هزینه (Cost) بهسمت بینهایت میرود.
شکل خلاصهشدهی تابع هزینهای که در بالا داشتیم بهاین شکل خواهد بود:


گرادیان نزولی (Gradient Descent)
حال سؤالی که برایمان پیش میآید این است که چطور باید این خطا یا هزینهای را که با تابع هزینه به دست آوردیم کاهش دهیم تا خروجی ما بهینه شود؟
پاسخ الگوریتم گرادیان نزولی (Gradient Descent) است که فرمول آن بهاین شکل است:


که در آن مشتق زنجیرهای هر پارامتر (در اینجا β₀ و β₁) را نسبت با خطای بهدستآمده میگیریم و درنهایت مقدار مشتق را از مقدار پارامتر قبلی کم میکنیم تا آن را بهروزرسانی کنیم. این کار چندین بار تکرار میشود تا زمانیکه پارامترهای ما بهینه شوند و خروجی مدل ما نتیجهی چشمگیری داشته باشد.
گرادیان نزولی یک قیاس دارد که در آن ما خود را در بالای کوهی تصور میکنیم، درحالیکه چشمانمان بسته است. هدف ما رسیدن به پایین کوه است. برای اینکه به پایین کوه برسیم باید سراشیبی را قدمبهقدم بهسمت پایین برویم. این عمل به محاسبهی گرادیان نزولی شبیه است و برداشتن یک قدم به هر بار بهروزرسانی پارامترها مشابه است.
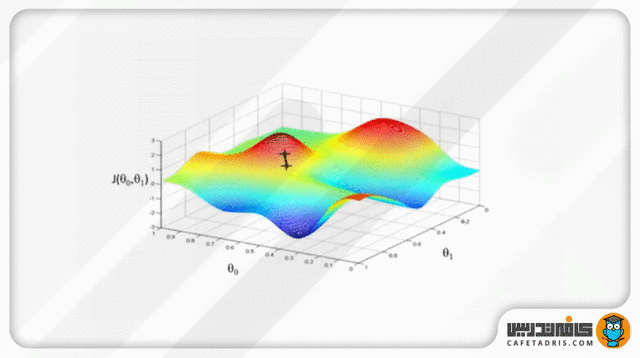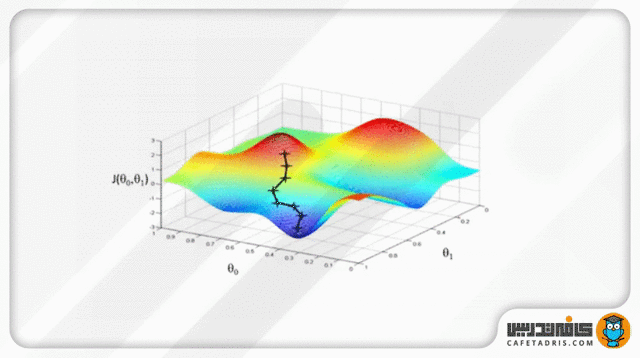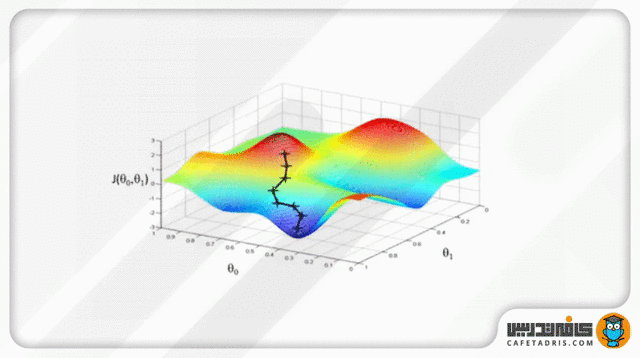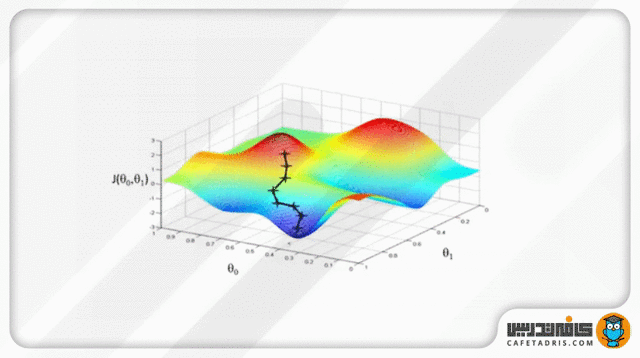

قسمتی از جزوه کلاس برای آموزش Logistic Regression
دوره جامع دیتا ساینس و ماشین لرنینگ

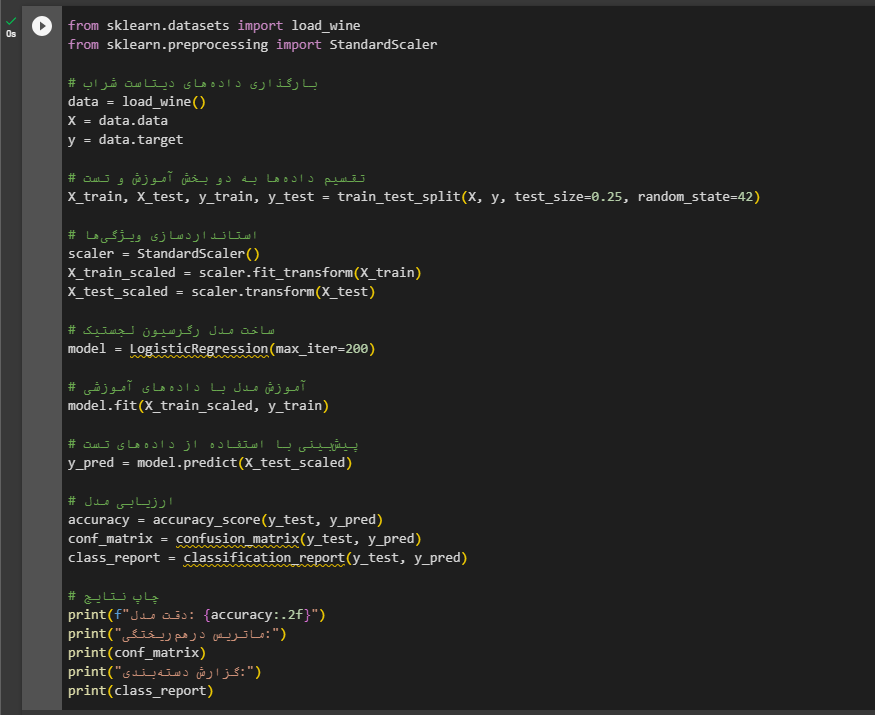
Logistic Regression در پایتون

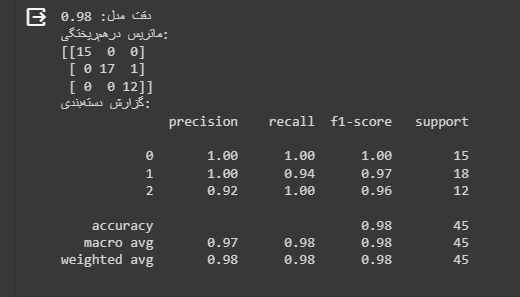

خلاصهی مطالب دربارهی رگرسیون لجستیک (Logistic Regression)
در این مطلب یکی از مشهورترین الگوریتمهای یادگیری ماشین، یعنی رگرسیون لجستیک، را معرفی کردیم. همانطور که متوجه شدیم، رگرسیون لجستیک برای کار طبقهبندی (Classification) استفاده میشود و نباید بهدلیل اینکه آن را رگرسیون مینامیم، با رگرسیون خطی اشتباه گرفته شود. در رگرسیون خطی هدف پیشبینی مقادیر پیوسته در خروجی است، درحالیکه در رگرسیون لجستیک هدف پیشبینی مقادیر گسسته است و در آن قصد داریم دادهها را به دو یا چند کلاس مشخص طبقهبندی کنیم.
رگرسیون لجستیک یکی از الگوریتمهایی است که تمامی افرادی که میخواهند یادگیری و کار در حوزهی یادگیری ماشین (Machine Learning) و علم داده (Data Science) را شروع کنند حتماً بهسراغش میروند. حال شما هم جزو کسانی هستید که این الگوریتم را بهخوبی میشناسید!



خیلی عالی بود همین جوری ادامه بدین. دستتون طلاااااااااااا
ممنون از توجه شما
قدر زر زرگر شناسد
قدر گوهر, گوهری
برخی افراد که مرتب تکرار کرده اند فلان شخص این بحث را طرح کرده, چیزی از ارزش آموزش ایشان ولو ترجمه باشد کم نمی کند. ایمیل مدرس محترم چیست
از حسن نظر شما ممنونم. برای ارتباط با استاد شکرزاد میتونین به تلگرام ایشون پیام بدین.
خیلی عالی بود. ممنونم
در واقع این همان دوره ی اموزشی Andrew ng هست و اون خودش بهتر توضیح میده . برید خود کلاسش رو در کورسرا یا مکتب خونه ببینید.
بله Andrew Ng هم توی دورهی ماشبنلرنینگش مبحث رگرسیون لجستیک رو آموزش داده. معمولا اکثر افراد از همین مثال برای توضیح مبحث رگرسیون لجستیک استفاده میکنن.
عالی
ممنون از اشتراک نظرتون.
به ساده ترین و درست ترین شکل ممکن توضیح دادین
موفق باشین
ممنون از اینکه نظرتون رو با ما به اشتراک گذاشتین دوست عزیز.
سلام خیلی مطالب مفید و خوب بود
خوشحالیم که اینطور بوده.