توابع فعالساز (Activation Functions) چیست و چه کاربردهایی دارد؟

توابع فعالساز (Activation Functions) چیست؟ مطمئناً در حین یادگیری و کار با شبکه‌های عصبی (Neural networks) بارها با توابع فعال‌ساز برخورد کرده‌اید و این سؤال در ذهن‌تان مطرح شده است که این توابع دقیقاً چه کاری را در شبکه انجام می‌دهند؟ در این مطلب سعی کرده‌ایم تا با بیانی ساده توابع فعال‍ساز را توضیح دهیم.

شبکه‌های عصبی چطور کار می‌کنند؟

شبکه‌های عصبی مدل‌های پردازش اطلاعات هستند که از روی نحوه‌ی کار سیستم‌های عصبی زیستی الهام گرفته شده‌اند. این شبکه‌ها چندین لایه از نودها یا نورون‌های متصل‌به‌هم را دربرمی‌گیرند که اطلاعات در طول آن‌ها از سمت لایه ورودی به‌سمت لایه‌های نهان و سپس لایه‌های خروجی حرکت می‌کند. در این شکل نمای یک شبکه عصبی را مشاهده می‌کنید:

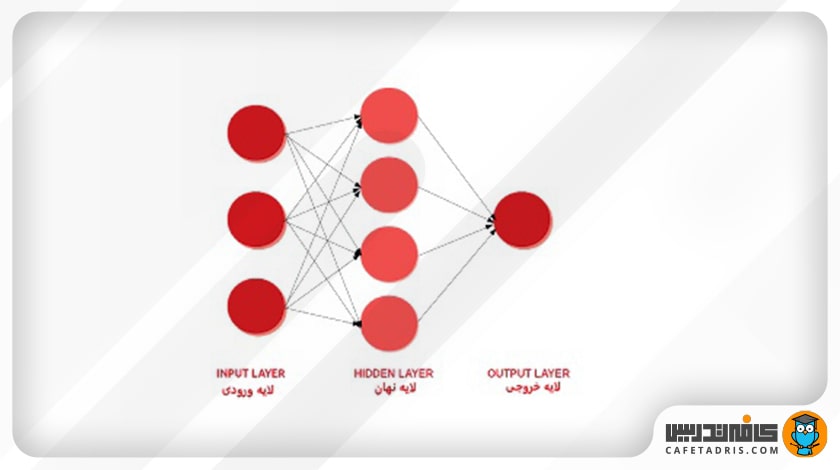
در هر لایه نحوه‌ی کار هر نورون به‌این شکل است که ابتدا مقادیر ورودی در وزن متناظر خود ضرب و با یک مقدار ثابت بایاس (Bias) جمع می‌شود؛ درنهایت نتیجه‌ی این ضرب به یک تابع فعال‌ساز وارد و خروجی آن به لایه‌ی بعدی منتقل می‌شود. این فرایند تا زمانی‌که به لایه‌ی آخر برسیم هم‌چنان تکرار می‌شود.

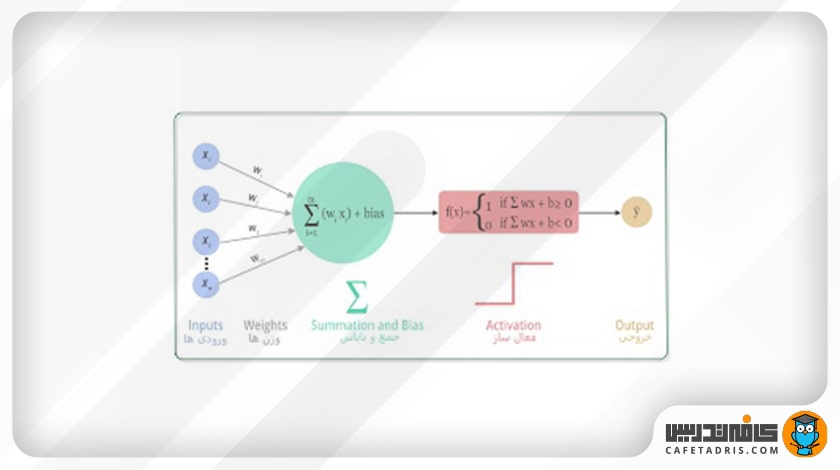
توابع فعالساز (Activation Functions) چیست؟

توابع فعالساز درواقع مانند گِیتی هستند که در هر نورون وجود دارد. ورودی این گِیت همان ورودی‌های هر نورون در هر لایه است (در وزن‌های متناظر خود ضرب شده‌اند و با مقدار ثابت بایاس جمع شده‌اند) و خروجی آن به لایه‌ی بعدی منتقل می‌شود. تابع فعالساز تصمیم می‌گیرد هر نورون فعال شود یا نه.

در این شکل یک نورون را مشاهده می‌کنیم:

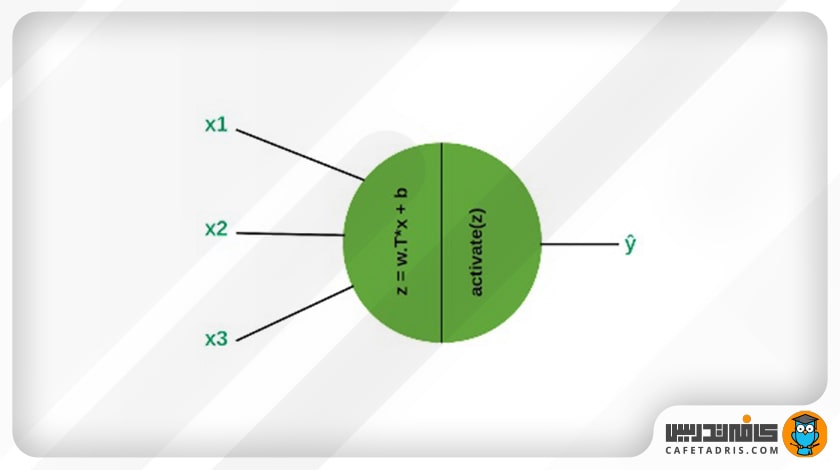
چرا از توابع فعالساز استفاده می‌کنیم؟

اگر از توابع فعالساز (Activation Functions) استفاده نکنیم، وزن‌ها و مقدار بایاس فقط یک معادله‌ی خطی را ایجاد می‌کنند. درست است که معادله‌ی خطی خیلی راحت‌تر حل‌شدنی است، اما برای حل مسائل پیچیده نمی‌تواند کمکی به ما کند؛ درواقع معادلات خطی در یادگیری الگوهای پیچیده‌ی داده‌ی خیلی محدود هستند و یک شبکه‌ی عصبی بدون تابع فعال‌ساز فقط یک مدل رگرسیون خطی (Linear Regression Model) است. به‌طور کلی، شبکه‌های عصبی از توابع فعالساز استفاده می‌کنند تا بتوانند به شبکه در یادگیری داده‌های پیچیده کمک و پیش‌بینی قابل‌قبولی را در خروجی ارائه کنند.

پیشنهاد می‌کنیم با رگرسیون خطی (Linear Regression) بیشتر آشنا شوید.

انواع تابع فعالساز چیست؟

به‌طور کلی می‌توان توابع فعالساز (Activation Functions) را به دو دسته تقسیم کرد:

• تابع فعال‌ساز خطی (Linear or Identity Activation Function)
• توابع فعال‌ساز غیرخطی (Non-linear Activation Functions)

تابع فعالساز خطی

این تابع دقیقاً جمع وزن‌دار ورودی هر نود را عیناً برمی‌گرداند و مقادیر را در بازه‌ی خاصی قرار نمی‌دهد.

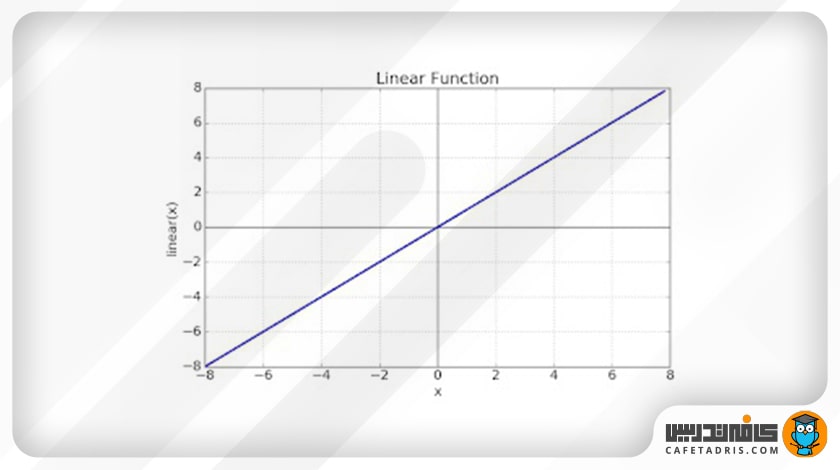
معادله: f(x) = x

بازه: (-∞,+∞)

همان‌طور که قبلاً اشاره کردیم، این نوع توابع نمی‌توانند به پردازش داده‌هایی با پیچیدگی بالا کمک کنند.

تابع فعالساز غیرخطی

شبکه‌های عصبی جدید از توابع فعالساز غیرخطی استفاده می‌کنند. این توابع به مدل کمک می‌کنند تا نگاشت‌های پیچیده را میان ورودی‌ها و خروجی‌های شبکه به وجود آورد؛ به‌عبارت دیگر، این توابع به مدل این امکان را می‌دهند تا خود را با داده‌های پیچیده و غیرخطی وفق دهد. این موضوع برای داده‌های پیچیده‌ای، مانند عکس، ویدئو، صدا و غیره، بسیار مهم است. در اکثر مواقع توابع فعالساز غیرخطی در شبکه‌های عصبی استفاده می‌شوند. توابع فعالساز غیرخطی انواع مختلفی دارند که در ادامه پرطرفدارترین آن‌ها را شرح می‌دهیم.

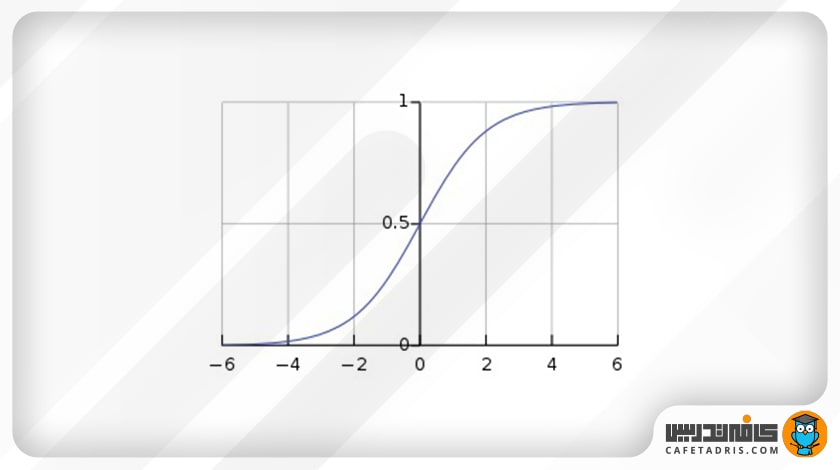
1. تابع سیگموید (Sigmoid)

این تابع یک منحنی S شکل است. زمانی‌که می‌خواهیم خروجی مدل احتمال باشد، از تابع سیگموید استفاده می‌کنیم؛ چون تابع سیگموید مقادیر را به بازه صفر تا ۱ می‌برد و احتمالات هم میان همین بازه قرار دارند.

مزایا

• این تابع تمایزپذیر (Differentiable) است؛ یعنی در هر قسمت از منحنی می‌توانیم شیب میان دو نقطه را حساب کنیم.
• از آنجا که این تابع مقادیر را میان صفر و یک قرار می‌دهد، نوعی عادی‌سازی را برای خروجی هر نورون انجام می‌دهد.

معایب

• با محوشدگی گرادیان (Vanishing Gradient) مقادیر بسیار بزرگ یا بسیار کوچک x، مشتق بسیار کوچک می‌شود و درواقع شبکه دیگر آموزش نمی‌بیند و پیش‌بینی‌هایش در خروجی ثابت می‌ماند.
• به‌دلیل مشکل محوشدگی‌گرادیان، تابع سیگموید هم‌گرایی کند دارد.
• خروجی تابع سیگموید صفرمحور (Zero-Centered) نیست؛ این امر کارایی به‌روزرسانی وزن‌ها را کم می‌کند.
• از آنجا که این تابع عملیات نمایی (Exponential Operations) دارد، می‌توان گفت هزینه‌ی محاسباتی بالایی دارد و کندتر پیش می‌رود.

معادله: (f(x) = s= 1/(1+e⁻ˣ

بازه: (0,1)

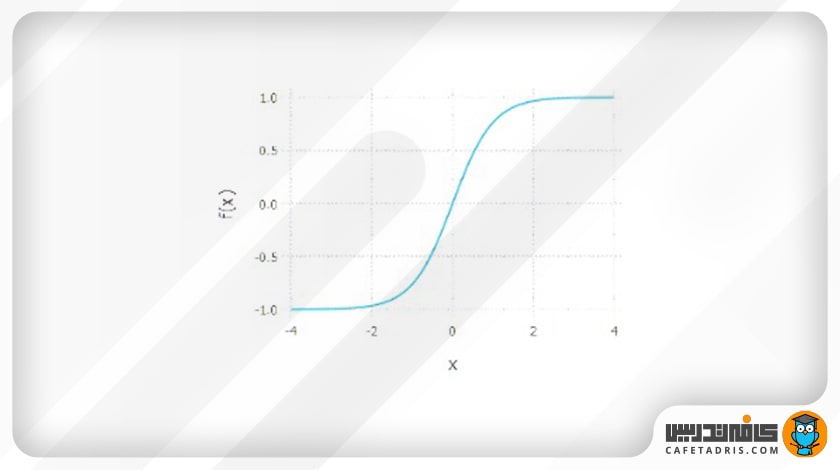
۲. تابع تانژانت هایپربولیک (Tanh, Hyperbolic Tangent)

این تابع هم مانند تابع سیگموید به‌شکل S است، اما در مقایسه با تابع سیگموید، نکات مثبت بیشتری دارد.

مزایا

• این تابع صفرمحور است؛ بنابراین به مدل کمک می‌کند تا مقادیر ورودی منفی، خنثی و مثبت داشته باشد؛ به‌عبارت دیگر، مقادیر منفی، به‌شدت منفی و مقادیر صفر در گراف تانژانت هایپربولیک نزدیک به صفر نگاشت می‌شوند.
• تابع آن یکنواخت (Monotonic)، اما مشتق آن یکنواخت نیست.

معایب

• محوشدگی گرادیان
• هم‌گرایی کند

معادله: (f(x) = a =tanh(x) =(eˣ – e⁻ˣ)/(eˣ +e⁻ˣ

بازه: (1, 1-)

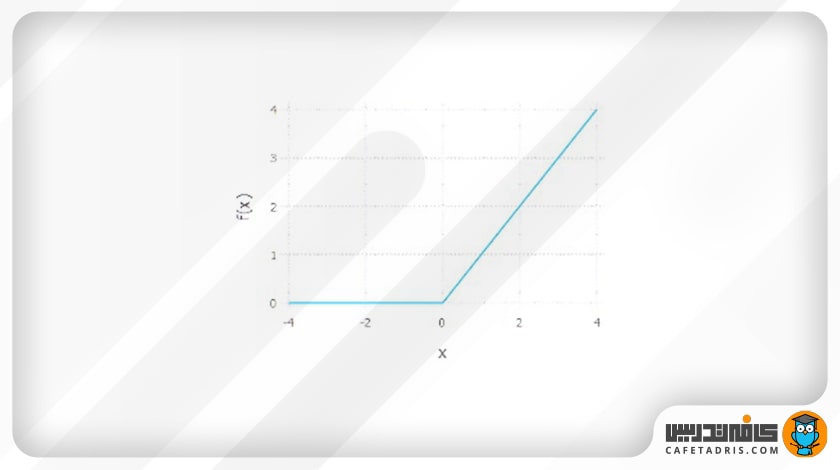
۳. تابع واحد یک‌سوشده‌ی خطی (ReLU / Rectified Linear Unit)

تابع فعالساز واحد یک‌سوشده‌ی خطی در زمینه‌ی یادگیری عمیق بسیار مشهور است و در بیشتر مواقع استفاده می‌شود. این تابع به‌این صورت عمل می‌کند که مقادیر منفی (زیر صفر) را صفر و مقادیر مثبت (بیشتر از صفر) و مقادیر برابر با صفر را همان مقدار خودش در نظر می‌گیرد.

مزایا:

• از نظر محاسباتی بسیار کارآمد است و به شبکه اجازه می‌دهد به‌سرعت همگرا شود؛ زیرا رابطه‌ی آن خطی است و به‌همین دلیل، در مقایسه با تابع‌های سیگموید و Tanh، سریع‌تر است.

معایب:

• مشکل مرگ نورون یا مرگ ReLU دارد؛ یعنی زمانی‌که ورودی صفر یا نزدیک به صفر باشد، تابع ReLU دیگر عملکردی ندارد و به‌بیان دیگر، می‌میرد. در این صورت، مقدار گرادیان تابع صفر می‌شود و شبکه نمی‌تواند عملیات پس انتشار (Backpropagation) را انجام دهد و آموزش ببیند.
• خروجی این تابع صفر یا مثبت است و این یعنی صفرمحور نیست.

معادله: (f(x) = a =max(0,x

بازه: (∞+,0)

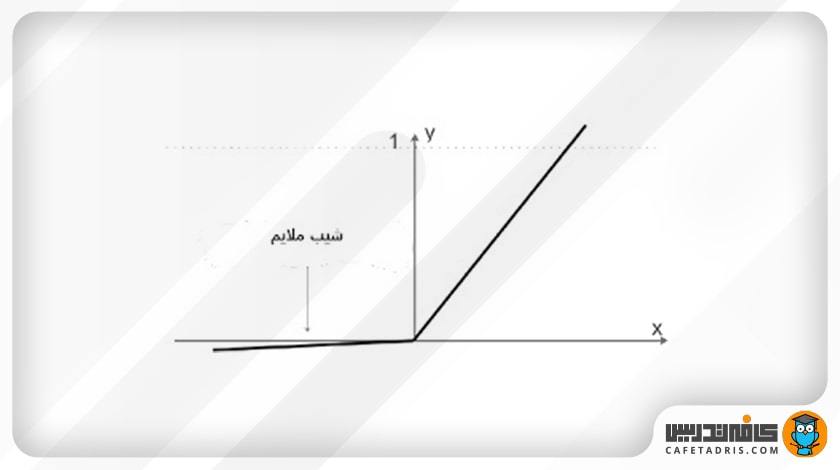
۴. تابع فعالساز Leaky ReLU

این تابع فعالساز برای حل مشکل اصلی تابع ReLU ارائه شده است. در شکل بعدی نمایی از این تابع را مشاهده می‌کنیم:

مزایا

• از مشکل مرگ ReLU جلوگیری می‌کند. این تابع یک شیب مثبت ملایم به‌سمت مقادیر منفی دارد که این امر باعث می‌شود عملیات پس انتشار (Backpropagation) حتی برای مقادیر منفی هم انجام شود.

معایب

• برای مقادیر منفی پیش‌بینی (خروجی) ثابتی را ارائه نمی‌کند.
• در حین عملیات انتشار روبه‌جلو (Forward Propagation) اگر نرخ یادگیری (Learning Rate) را خیلی بالا در نظر بگیریم، مشکل مرگ نورون‌ها را رقم می‌زند.

معادله: (f(x)= a = max(0.01x, x

بازه: (∞+, 0.01)

۵. تابع سافت‌مکس (Softmax)

این تابع فعالساز از جمله توابع فعالساز (Activation Functions) است که در طبقه‌بندی‌های چندکلاسه استفاده می‌شود. زمانی‌که احتیاج داشته باشیم در خروجی احتمال عضویت بیشتر دو کلاس را پیش‌بینی کنیم، می‌توانیم به‌سراغ این تابع برویم. تابع سافت‌مکس تمامی مقادیر یک بردار با طول K را به بازه‌ی صفر تا ۱ می‌برد، به‌طوری که جمع تمامی مقادیر این بردار با هم ۱ می‌شود. این تابع برای نورون‌های لایه‌ی خروجی استفاده می‌شود؛ زیرا در شبکه‌های عصبی در آخرین لایه (خروجی) به طبقه‌بندی ورودی‌ها در کلاس‌های مختلف نیاز داریم.

مزایا

• این تابع قابلیت استفاده در تسک های چندکلاسه را دارد. خروجی هر کلاس را میان صفر تا ۱ عادی‌سازی می‌کند؛ سپس آن‌ها را بر مجموعه‌شان تقسیم و احتمال عضویت مقادیر ورودی را در هر کلاس به ما در خروجی ارائه می‌کند.

معایب

• مقدار گرادیان برای مقادیر منفی صفر است؛ به‌این معنا که وزن‌ها در حین عملیات پس‌انتشار به‌روزرسانی نمی‌شوند و این می‌تواند مشکل مرگ نورون را ایجاد کند.

معادله: (f(x) = eˣᵢ / (Σⱼ₌₀eˣᵢ

بازه: (1,0)

فرق بین تابع sigmoid و softmax

هر دو  تابع softmax و sigmoid توابع ریاضی هستند که در یادگیری ماشین و شبکه‌های عصبی مصنوعی برای اهداف مختلف استفاده می‌شوند.

تابع sigmoid یک تابع فعالساز رایج است که هر عدد را می‌گیرد و آن را به مقداری بین 0 و 1 ترسیم می‌کند.

Sigmoid اغلب در مسائل طبقه‌بندی باینری استفاده می‌شود، جایی که خروجی مدل باید به عنوان احتمال کلاس مثبت تفسیر شود. با این حال، سیگموید از مشکل محوشدگی گرادیان رنج می‌برد، که می‌تواند آموزش شبکه‌های عصبی عمیق‌تر را دشوار کند.

از طرف دیگر، تابع softmax یک تابع کلی‌تر است که می‌تواند برای تبدیل بردار اعداد واقعی به توزیع احتمال استفاده شود. یک بردار ورودی می‌گیرد و یک توزیع احتمال روی K کلاس را در خروجی می‌دهد، که در آن K تعداد کلاس‌ها است.

Softmax اغلب به عنوان تابع فعال‌ساز لایه خروجی در مسائل طبقه‌بندی چند کلاسه استفاده می‌شود، جایی که هدف، پیش‌بینی احتمال هر کلاس است. همچنین در پردازش زبان طبیعی برای مدل‌سازی زبان و وظایف طبقه‌بندی متن استفاده می‌شود.

به طور خلاصه، sigmoid یک تابع فعالساز باینری است که در مسائل طبقه‌بندی باینری استفاده می‌شود، در حالی که softmax یک تابع فعالساز چند کلاسه است که در مسائل طبقه‌بندی چند کلاسه استفاده می‌شود.

کدام تابع فعالساز را انتخاب کنیم؟

حال که با چندین مورد توابع فعالساز (Activation Functions) مشهور در شبکه‌های عصبی آشنا شدیم، قطعاً این سؤال را در ذهن داریم که باید از کدام‌یک از این توابع استفاده کنیم؟

جواب این سؤال به فاکتورهای بسیار زیادی بستگی دارد و نمی‌توان یک تابع را برای تمامی تسک‌ها مفید و کاربردی دانست، اما شاید این موارد بتواند تا حدی به کمک‌مان بیاید:

• تابع سیگموید (Sigmoid) در مسائل طبقه‌بندی معمولاً خیلی خوب عمل می‌کند.
• توابع سیگموید (Sigmoid) و تانژانت هایپربولیک (Tanh)، به‌دلیل مشکل محوشدگی گرادیان، در بعضی مواقع استفاده نمی‌شوند.
• تابع فعالساز واحد یک‌سوشده‌ی خطی (ReLU) بیشتر از باقی استفاده می‌شود و نتایج خوبی را در خروجی ارائه می‌کند.
• تابع فعالساز واحد یک‌سوشده‌ی خطی (ReLU) فقط در لایه‌های نهان (Hidden Layers) استفاده می‌شود.
• اگر با مشکل مرگ نورون در شبکه مواجه هستیم، تابع Leaky ReLU می‌تواند گزینه‌ی بسیار خوبی باشد.
• تابع تانژانت هایپربولیک (Tanh)، به‌دلیل مشکل مرگ نورون، کمتر استفاده می‌شود.

یادگیری علم داده با کلاس‌های آنلاین آموزش علم داده کافه‌تدریس

اگر علاقه دارید علم داده و یادگیری ماشین را یاد بگیرید، پیشنهاد ما شرکت در کلاس‌های آنلاین آموزش علم داده کافه‌تدریس است.

کافه‌تدریس به‌صورت جامع کلاس‌های آنلاین آموزش داده را در دوره‌های مقدماتی و پیشرفته برگزار می‌کند. دوره‌ی جامع علم داده کافه‌تدریس به‌صورت پویا و تعاملی برگزار می‌شود و مبتنی بر کار روی پروژه‌های واقعی علم داده است.

برای آشنایی با کلاس‌های آنلاین آموزش علم داده کافه‌تدریس و مشاوره‌ی رایگان برای شروع یادگیری روی این لینک کلیک کنید:

دوره جامع یادگیری علم داده (Data Science)