با الگوریتم DBSCAN آشنا شوید!

یادگیری ماشین شاخه‌ای از هوش مصنوعی است که به کامپیوترها توانایی یادگیری و بهبود عملکرد براساس تجربه‌های گذشته بدون برنامه‌ریزی صریح می‌دهد. این فناوری از الگوریتم‌ها و مدل‌های آماری برای تحلیل و پردازش داده‌ها استفاده می‌کند تا الگوهای پنهان را کشف و پیش‌بینی‌های دقیقی ارائه کند. در این مطلب با الگوریتم DBSCAN و چگونگی شناسایی شکل‌های نامنظم در داده‌ها در این الگوریتم آشنا می‌شویم.

معرفی الگوریتم DBSCAN

DBSCAN که مخفف Density-Based Spatial Clustering of Applications with Noise است یک الگوریتم بدون ناظر خوشه‌بندی مبتنی بر تراکم است که برای یافتن خوشه‌ها در داده‌ها با توجه به تراکم آن‌ها طراحی شده است. این الگوریتم قادر است خوشه‌های با اشکال متفاوت را تشخیص دهد و نسبت به نویز و نقاط پرت مقاوم باشد. DBSCAN، به‌دلیل نیازنداشتن به تعیین تعداد خوشه‌ها قبل از اجرای الگوریتم و توانایی کار با داده‌های با تراکم متفاوت، به‌عنوان یک روش خوشه‌بندی انعطاف‌پذیر و کارآمد شناخته می‌شود. این الگوریتم در زمینه‌های مختلفی مانند تحلیل داده‌های مکانی، شناسایی انواع الگوها در داده‌های پیچیده و بسیاری موارد دیگر کاربرد دارد.

تاریخچه DBSCAN

DBSCAN اولین بار در سال ۱۹۹۶ را Martin Ester, Hans-Peter Kriegel, Jörg Sander و Xiaowei Xu معرفی کردند. این الگوریتم در پاسخ به نیاز برای خوشه‌بندی داده‌ها در فضاهای با ابعاد بالا و با تراکم‌های متفاوت طراحی شد. DBSCAN، برخلاف روش‌های قبلی، مانند K-Means که به تعداد مشخصی از خوشه‌ها نیاز دارند، از داده‌های خود برای تعیین تعداد خوشه‌ها استفاده می‌کند. این الگوریتم به‌سبب توانایی‌اش در شناسایی خوشه‌ها با اشکال و اندازه‌های مختلف و مقاومت دربرابر نویز محبوبیت زیادی کسب کرده است.

اصول اولیه DBSCAN

DBSCAN بر اساس دو مفهوم کلیدی کار می‌کند: تراکم (Density Reachability) و همسایگی (Density Connectivity). تراکم در این الگوریتم به‌معنای تعداد نقاط در یک شعاع معین (معمولاً نشان داده شده با ε) است. یک نقطه هسته زمانی تعریف می‌شود که تعداد مشخصی از همسایه‌ها (حداقل نقاط) در شعاع ε از آن قرار داشته باشند. نقاطی که در شعاع ε از یک نقطه هسته قرار دارند اما خودشان به عنوان نقطه هسته عمل نمی‌کنند، نقاط مرزی نامیده می‌شوند. نقاطی که به هیچ یک از این دو دسته تعلق ندارند به‌عنوان نویز در نظر گرفته می‌شوند.

DBSCAN شروع به ایجاد خوشه‌ها می‌کند با تعیین نقاط هسته و سپس گسترش خوشه‌ها با افزودن نقاط مرزی به نزدیک‌ترین نقطه هسته. این روند ادامه می‌یابد تا زمانی که دیگر نقطه هسته جدیدی برای اضافه‌کردن به خوشه‌ها باقی نماند. یکی از ویژگی‌های برجسته DBSCAN توانایی آن در تشخیص خوشه‌ها با اندازه‌ها و شکل‌های مختلف است، که این امر آن را ابزاری متنوع و قدرتمند در زمینه تحلیل داده‌های پیچیده می‌کند.

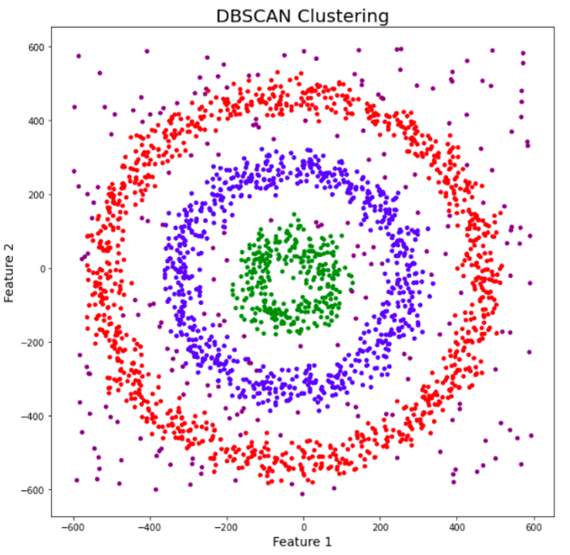
چگونگی کارکرد DBSCAN

• تعریف نقاط هسته (یک کلاستر): در الگوریتم DBSCAN، نقاط هسته نقاطی هستند که حداقل تعداد معینی از همسایه‌ها در فاصله مشخصی از آن‌ها قرار دارند. این فاصله به وسیله پارامتر اپسیلون (ε) تعیین می‌شود و تعداد همسایه‌ها با پارامتر MinPts مشخص می‌شود. نقاط هسته نقش محوری در تشکیل خوشه‌ها دارند.

• تعریف نقاط مرزی: نقاط مرزی نقاطی هستند که در فاصله ε از یک نقطه هسته قرار دارند، اما خودشان به‌تنهایی تعداد کافی همسایه در این فاصله ندارند تا به‌عنوان یک نقطه هسته شناخته شوند. این نقاط به خوشه‌ای که نقطه هسته آن در آن قرار دارد تعلق می‌گیرند.

فرآیند الگوریتم DBSCAN

1. انتخاب نقطه شروع: الگوریتم یک نقطه تصادفی از مجموعه داده‌ها را انتخاب می‌کند.
2. بررسی همسایگان: تمام نقاط در فاصله ε (اپسیلون) از نقطه انتخاب‌شده بررسی می‌شوند تا تعیین شود که آیا آن‌ها همسایه‌های نقطه هستند یا خیر.
3. تعیین وضعیت نقطه انتخابی: اگر تعداد همسایه‌ها بیشتر از یا برابر با MinPts (حداقل تعداد نقاط موردنیاز برای تشکیل یک خوشه) باشد، نقطه انتخابی به عنوان یک نقطه هسته تعیین می‌شود.
4. تشکیل خوشه: اگر نقطه انتخابی یک نقطه هسته باشد، خوشه‌ای جدید ایجاد می‌شود و همسایه‌های آن به خوشه اضافه می‌شوند.
5. گسترش خوشه: الگوریتم همسایه‌های هر نقطه هسته را بررسی می‌کنند و اگر آن‌ها نیز معیارهای یک نقطه هسته را دارا باشند، به همان خوشه اضافه می‌شوند.
6. تکرار فرایند: این فرایند تکرار می‌شود تا تمامی نقاطی که به نقطه هسته یا نقاط همسایه تعلق دارند در خوشه‌ها قرار گیرند.
7. تعیین نویز: نقاطی که به‌عنوان نقطه هسته یا مرزی شناسایی نمی‌شوند و در هیچ خوشه‌ای قرار نمی‌گیرند، به‌عنوان نویز در نظر گرفته می‌شوند.

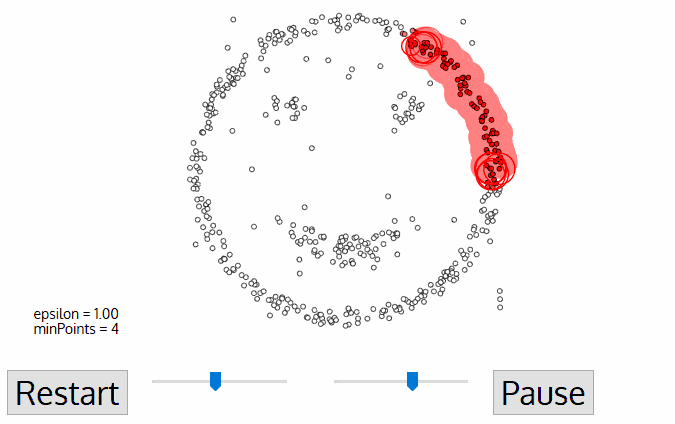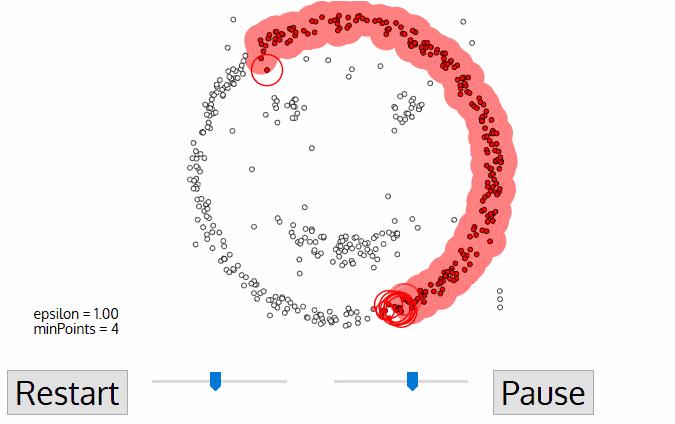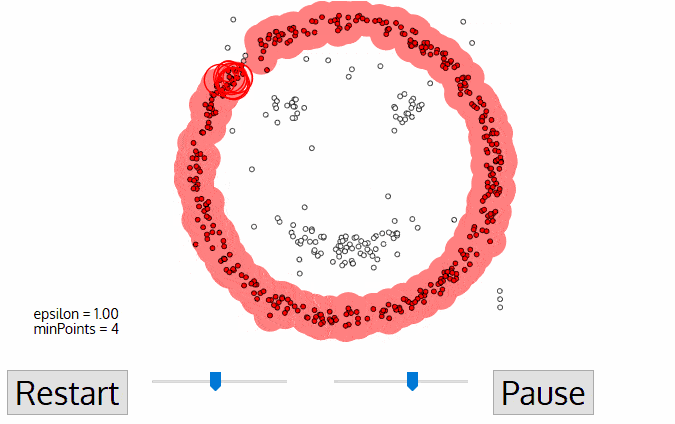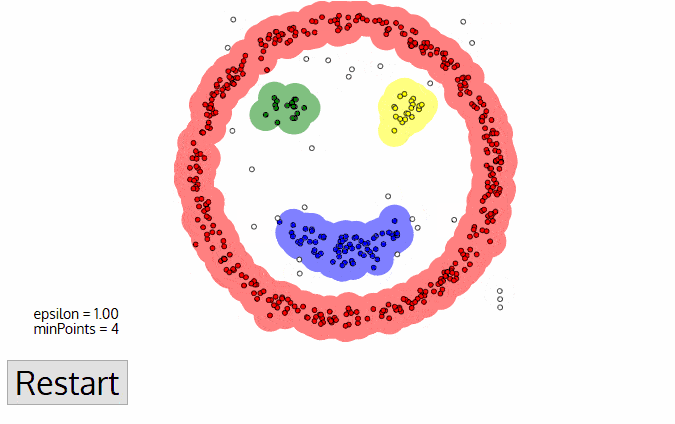
مزیت‌های DBSCAN

برخی از مزیت‌های DBSCAN از این قرار است:

توانایی در یافتن خوشه‌های با شکل‌های متنوع

یکی از بارزترین ویژگی‌های الگوریتم DBSCAN توانایی آن در تشخیص خوشه‌های با اشکال و اندازه‌های گوناگون است. درحالی‌که بسیاری از الگوریتم‌های دیگر خوشه‌بندی، مانند K-Means، بیشتر در شناسایی خوشه‌های کروی یا دایره‌ای شکل موفق عمل می‌کنند، DBSCAN قادر است خوشه‌هایی با شکل‌های نامنظم و پیچیده را نیز تشخیص دهد. این قابلیت باعث می‌شود که DBSCAN در موقعیت‌هایی که داده‌ها توزیع نامتقارن دارند بسیار کارآمد باشد.

مقاومت دربرابر نقاط پرت

DBSCAN همچنین دربرابر نقاط پرت یا داده‌های نویزی بسیار مقاوم است. در الگوریتم‌های خوشه‌بندی دیگر وجود نقاط دورافتاده می‌تواند بر تشکیل خوشه‌ها و تفسیر نتایج تأثیر منفی گذارد، اما DBSCAN با تعریف دقیق نقاط هسته و نقاط مرزی، از اینکه نقاط پرت به‌اشتباه به‌عنوان بخشی از یک خوشه در نظر گرفته شوند جلوگیری می‌کند. این ویژگی باعث می‌شود که DBSCAN در محیط‌هایی با داده‌های ناپایدار و پیچیده یک انتخاب ایده‌آل باشد.

محدودیت‌های DBSCAN

برخی از محدودیت‌های DBSCAN از این قرار است:

حساسیت به پارامترها

یکی از چالش‌های اصلی در استفاده از الگوریتم DBSCAN حساسیت آن به انتخاب پارامترها، به‌ویژه دو پارامتر اصلی ε (اپسیلون) و MinPts (حداقل تعداد نقاط)، است. اپسیلون که شعاع همسایگی را تعیین می‌کند و MinPts که دست‌کم تعداد نقاط لازم برای تشکیل یک خوشه را مشخص می‌کند، به‌طور مستقیم بر تشکیل خوشه‌ها تأثیر می‌گذارند. انتخاب نادرست این پارامترها می‌تواند به تشکیل خوشه‌های ناقص یا حذف نادرست نقاط به عنوان نویز بینجامد. به‌طور خاص، انتخاب یک مقدار بزرگ برای ε می‌تواند به ادغام خوشه‌های مجزا و انتخاب یک مقدار کوچک برای MinPts می‌تواند به نادیده‌گرفتن خوشه‌های با تراکم پایین بینجامد.

دشواری با تراکم‌های متفاوت

DBSCAN در کار با داده‌هایی که تراکم ناهمگن دارند یعنی مناطقی از داده‌ها که تراکم بسیار بالا و مناطق دیگر که تراکم بسیار پایین دارند با مشکل مواجه است. در چنین وضعیتی تنظیم پارامترهایی که برای تمامی بخش‌های داده‌ها به‌خوبی کار کند دشوار است؛ برای مثال، یک مقدار ε که برای خوشه‌های با تراکم بالا مناسب است، ممکن است باعث از دست دادن خوشه‌های با تراکم پایین شود. این محدودیت باعث می‌شود که DBSCAN در مواجهه با داده‌هایی با تراکم‌های متفاوت به انعطاف‌پذیری کمتری داشته باشد و نیازمند تنظیم دقیق‌تر پارامترها باشد.

این دو محدودیت نشان‌دهنده اهمیت تنظیم دقیق پارامترها و دشواری‌هایی است که ممکن است در کار با داده‌های دارای تراکم‌های متفاوت با الگوریتم DBSCAN به وجود آید. درحالی‌که DBSCAN در بسیاری از موارد بسیار کارآمد است، این محدودیت‌ها باید هنگام انتخاب آن به عنوان ابزار خوشه‌بندی در نظر گرفته شوند.

کاربرد‌های DBSCAN

الگوریتم DBSCAN، به‌دلیل توانایی‌اش در شناسایی خوشه‌ها با اشکال مختلف و مقاومت دربرابر نویز، در زمینه‌های گوناگونی استفاده می‌شود. ازجمله کاربردهای برجسته‌ی این الگوریتم می‌توان به تشخیص کلاهبرداری در تراکنش‌های مالی، تجزیه‌وتحلیل داده‌های بیوانفورماتیک، مدیریت و دسته‌بندی اطلاعات ژئومکانیکی و شناسایی گروه‌های اجتماعی در شبکه‌های اجتماعی اشاره کرد. در هر یک از این موارد DBSCAN با توجه به قابلیت خود در شناسایی الگوهای پیچیده و نامنظم امکان کشف دیدگاه‌های عمیق‌تر و دقیق‌تری را فراهم می‌آورد.

تشخیص کلاهبرداری

در حوزه تشخیص کلاهبرداری DBSCAN، به‌دلیل توانایی تشخیص خوشه‌های نامنظم و غیرعادی، به‌کار گرفته می‌شود. این الگوریتم قادر است الگوهای غیرمعمول در تراکنش‌های مالی را شناسایی و موارد مشکوک را برای بررسی بیشتر مشخص کند.

بیوانفورماتیک

در بیوانفورماتیک DBSCAN برای تحلیل مجموعه‌های بزرگ داده‌های ژنتیکی و پروتئینی به کار می‌رود. این الگوریتم به محققان این امکان را می‌دهد که گروه‌ها و الگوهای پیچیده در داده‌ها را شناسایی کنند که می‌تواند به کشفیات جدید در زمینه‌ی بیماری‌ها و درمان‌های مرتبط بینجامد.

مدیریت اطلاعات ژئومکانیکی

DBSCAN در تجزیه‌وتحلیل داده‌های مکانی و جغرافیایی، مانند تشخیص الگوهای ترافیکی، بررسی توزیع جمعیتی و مدیریت منابع طبیعی، به کار رفته است. این الگوریتم با قابلیت شناسایی خوشه‌های با اشکال متنوع درک بهتری از توزیع و الگوهای مکانی ارائه می‌کند.

شبکه‌های اجتماعی

در شبکه‌های اجتماعی DBSCAN برای شناسایی گروه‌های کاربری با علایق مشابه یا الگوهای رفتاری مشترک استفاده می‌شود. این کاربرد می‌تواند به بهبود استراتژی‌های بازاریابی و ارائه محتوای مرتبط به کاربران کمک کند.

مقایسه الگوریتم DBSCAN با الگوریتم های دیگر

DBSCAN و K-Means

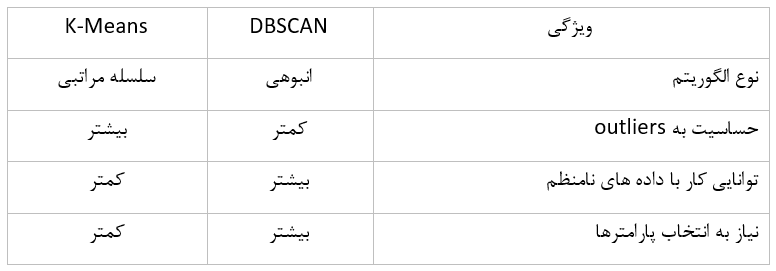
الگوریتم K-means یک الگوریتم خوشه‌بندی سلسله‌مراتبی است که براساس میانگین هندسی داده‌ها کار می‌کند. این الگوریتم به این فرضیه متکی است که خوشه‌ها مجموعه‌ای از نقاط داده هستند که به‌طور متوسط نزدیک به یکدیگر هستند. K-means یک الگوریتم سریع و آسان برای پیاده‌سازی است، اما محدودیت هایی دارد؛ برای مثال، این الگوریتم حساس به outliers است و نمی‌تواند به خوبی با خوشه های نامنظم کار کند.

الگوریتم DBSCAN، برخلاف K-means، یک الگوریتم خوشه بندی انبوهی است. این الگوریتم به این فرضیه متکی است که خوشه ها مناطق پرتراکمی در فضای داده هستند که توسط مناطق کم تراکم از یکدیگر جدا می شوند. DBSCAN می تواند با موفقیت روی داده‌های نامنظم کار کند و در شناسایی outliers نیز عملکرد بهتری دارد.

 DBSCAN با خوشه‌های نامنظم و توانایی رسیدگی به نقاط پرت و K-Means با خوشه‌های دایره‌ای با فاصله یکنواخت یک مقیاس تعادل در مرکز نماد مقایسه میان دو الگوریتم است.

برای آشنایی با الگوریتم k نزدیک‌ترین همسایه این مطلب را مطالعه کنید:

معرفی الگوریتم K-means

DBSCAN و Hierarchical Clustering

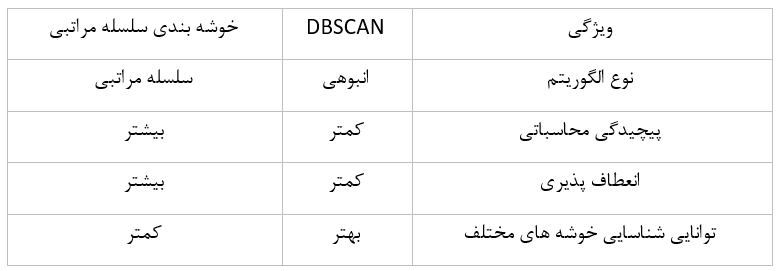
الگوریتم خوشه‌بندی سلسله‌مراتبی یک خانواده از الگوریتم های خوشه‌بندی است که شامل الگوریتم‌های مختلفی مانند Agglomerative clustering و Divisive clustering می‌شود. این الگوریتم‌ها خوشه‌ها را به‌طور تدریجی ایجاد می‌کنند، ابتدا خوشه‌ها را به خوشه‌های بزرگ‌تر ترکیب می‌کنند (در الگوریتم Agglomerative clustering) یا خوشه‌های بزرگ را به خوشه‌های کوچک تر تقسیم می‌کنند (در الگوریتم Divisive clustering). الگوریتم های سلسله‌مراتبی انعطاف‌پذیر هستند و می‌توانند با انواع مختلف داده‌ها کار کنند، اما می‌توانند پیچیده باشند و به محاسبات زیادی نیاز داشته باشند.

انتخاب پارامترهای DBSCAN: انتخاب Epsilon و تعیین حداقل تعداد نقاط

• ε (epsilon): این پارامتر فاصله نزدیکی را تعیین می‌کند که یک نقطه باید به یک نقطه دیگر داشته باشد تا آن‌ها را به‌عنوان همسایگان نزدیک در نظر بگیرد.
• minPts (حداقل تعداد نقاط): این پارامتر حداقل تعداد نقاطی را تعیین می‌کند که یک نقطه برای اینکه به‌عنوان یک نقطه مرکزی در نظر گرفته شود باید داشته باشد.

نحوه انتخاب Epsilon (ε)

پارامتر ε تعیین می‌کند که یک نقطه باید چقدر به دیگر نقاط نزدیک باشد تا به‌عنوان یک نقطه مرکزی در نظر گرفته شود. انتخاب یک مقدار مناسب برای ε به عوامل مختلفی مانند شکل خوشه‌ها و میزان پراکندگی داده‌ها بستگی دارد.

اگر ε خیلی کوچک باشد، بسیاری از نقاط به‌عنوان نقاط مرکزی در نظر گرفته می شوند و خوشه‌های کوچک و پراکنده ایجاد می‌شوند. اگر ε خیلی بزرگ باشد، تعداد نقاط مرکزی کمتر است و خوشه‌های بزرگ و نامنظم ایجاد می‌شوند.

یک روش معمول برای انتخاب ε استفاده از k-distance graph است. k-distance graph یک نمودار است که در آن فاصله هر نقطه از k-امین نزدیک‌ترین همسایه خود نمایش داده می‌شود. یک مقدار خوب برای ε معمولاً در ناحیه‌ای از نمودار k-distance graph قرار دارد که نشان‌دهنده تغییر ناگهانی در توزیع فاصله‌هاست.

تعیین حداقل تعداد نقاط (minPts)

پارامتر minPts تعیین می‌کند که یک نقطه برای اینکه به‌عنوان یک نقطه مرکزی در نظر گرفته شود باید دست‌کم چند همسایه نزدیک داشته باشد. انتخاب یک مقدار مناسب برای minPts به عوامل مختلفی، مانند شکل خوشه‌ها و میزان پراکندگی داده‌ها، بستگی دارد.

اگر minPts خیلی کوچک باشد، نقاط مرکزی زیادی ایجاد می‌شوند و خوشه ها کوچک و نامنظم هستند. اگر minPts خیلی بزرگ باشد، نقاط مرکزی کمتر است و ممکن است برخی از خوشه‌ها شناسایی نشوند.

یک روش معمول برای انتخاب minPts استفاده از تکنیک elbow method است. در این روش، minPts به‌طور تدریجی افزایش می‌یابد و تعداد خوشه‌هایی که شناسایی می‌شوند محاسبه می‌شود؛ سپس minPtsای انتخاب می‌شود که باعث ایجاد تعداد زیادی خوشه بدون افزایش قابل توجه در تعداد خوشه ها می‌شود.

الگوریتم DBSCAN در پایتون

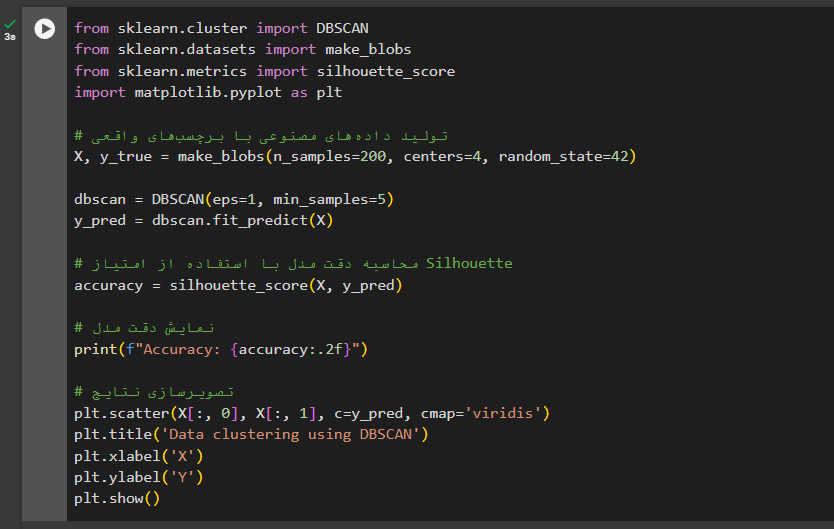
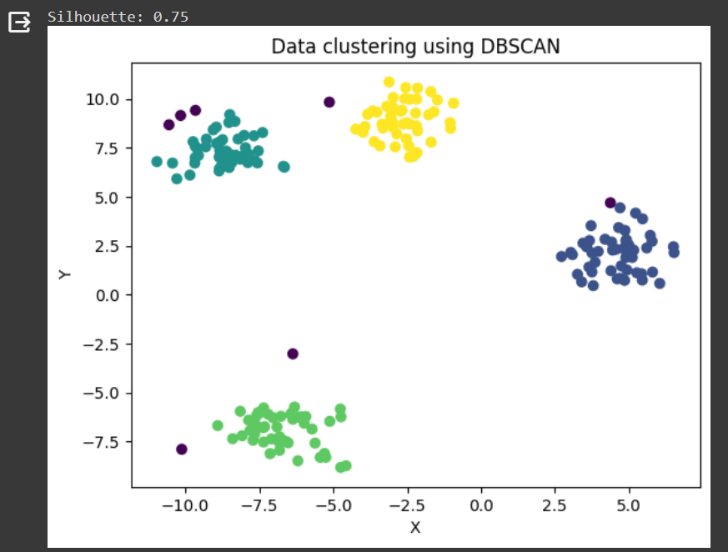
در این کد از الگوریتم DBSCAN برای خوشه‌بندی یک مجموعه داده‌های مصنوعی استفاده می‌کنیم. داده‌ها با استفاده از تابع make_blobs در کتابخانه sklearn تولید شده‌اند که شامل ۲۰۰ نمونه داده تصادفی با چهار مرکز مختلف هستند.

الگوریتم DBSCAN با پارامترهای eps=1 و min_samples=5 تنظیم شده است که eps فاصله حداکثری برای قرارگرفتن دو نقطه در یک خوشه و min_samples حداقل تعداد نقاط لازم برای تشکیل یک خوشه را مشخص می‌کند.

پس از اجرای DBSCAN بر روی داده‌ها، امتیاز Silhouette برای ارزیابی کیفیت خوشه‌بندی محاسبه می‌شود. این امتیاز نشان‌دهنده چگونگی تفکیک و تراکم خوشه‌هاست. درنهایت، نتایج خوشه‌بندی با استفاده از تصویرسازی نمایش داده می‌شوند که به ما امکان می‌دهد تا تقسیم‌بندی خوشه‌ها را به‌صورت بصری مشاهده کنیم.

خلاصه

در این مطلب ما به‌طور جامع الگوریتم DBSCAN در یادگیری ماشین را بررسی کردیم و درباره مفاهیم اساسی، چگونگی عملکرد، مزیت‌ها و محدودیت‌های الگوریتم، همچنین کاربردهای آن در دنیای واقعی مورد بحث کردیم. DBSCAN، به‌دلیل توانایی خود در شناسایی خوشه‌های با اشکال متنوع و مقاومت در برابر نویز، یک ابزار قدرتمند در تجزیه‌و تحلیلداده‌هاست؛ بااین‌حال انتخاب دقیق پارامترها برای بهره‌برداری کامل از توانایی‌های آن ضروری است.

پرسش‌های متداول

DBSCAN چگونه خوشه‌های داده‌ها را تشخیص می‌دهد؟

DBSCAN با تعریف نقاط هسته و مرزی و تجزیه داده‌ها براساس تراکم، خوشه‌ها را شناسایی می‌کند.

چرا انتخاب پارامترهای DBSCAN مهم است؟

پارامترهای مانند اپسیلون و حداقل نقاط تأثیر مستقیمی بر توانایی DBSCAN در تشخیص خوشه‌ها دارند.

DBSCAN در مقابل K-Means چه تفاوت‌هایی دارد؟

DBSCAN براساس تراکم کار می‌کند و به‌خوبی می‌تواند خوشه‌های با شکل‌های نامنظم را شناسایی کند، درحالی‌که K-Means بیشتر برای خوشه‌های دایره‌ای یا کروی مناسب است.

چگونه می‌توان DBSCAN را برای داده‌های بزرگ بهینه کرد؟

استفاده از ابزارها و الگوریتم‌های بهینه‌سازی می‌تواند در کاهش زمان محاسبات و بهبود کارایی DBSCAN در داده‌های حجیم مؤثر باشد.

آیا DBSCAN دربرابر نویز مقاوم است؟

بله، یکی از مزیت‌های اصلی DBSCAN مقاومت آن دربرابر نویز و نقاط پرت است که این امکان را فراهم می‌آورد تا خوشه‌ها را با دقت بیشتری تشخیص دهد.

یادگیری ماشین لرنینگ و دیتا ساینس را از امروز شروع کنید!

دنیای داده‌ها جذاب است و دانستن علم داده، توانایی تحلیل داده‌ یا بازاریابی مبتنی بر داده شما را برای فرصت‌های شغلی بسیاری مناسب می‌کند. فارغ از رشته‌ و پیش‌زمینه‌ شغلی و تحصیلی، می‌توانید حالا شروع کنید و این دانش از سطح مقدماتی تا پیشرفته بیاموزید. اگر دوست دارید به این حوزه وارد شوید، پیشنهاد می‌کنیم با کلیک روی این لینک قدم اول را همین حالا بردارید.

مشاوران کافه‌تدریس به شما کمک می‌کنند مسیر یادگیری برای ورود به این حوزه را شروع کنید:

دوره جامع دیتا ساینس و ماشین لرنینگ

هفت‌خوان: مطالعه کن، نظر بده، جایزه بگیر!

هفت‌خوان مسابقه‌ی وبلاگی کافه‌تدریس است. شما با پاسخ به چند پرسش درباره‌ی مطلبی که همین حالا مطالعه کرده‌اید، فرصت شرکت در قرعه‌کشی جایزه نقدی و کلاس رایگان کافه‌تدریس را پیدا خواهید کرد.

جوایز هفت‌خوان

• ۱,۵۰۰,۰۰۰ تومان جایزه نقدی
• ۳ کلاس رایگان ۵۰۰,۰۰۰ تومانی

پرسش‌های مسابقه

برای شرکت در هفت‌خوان کافه‌تدریس در کامنت همین مطلب به این پرسش‌ها پاسخ دهید:

• در مقایسه الگوریتم DBSCAN با K-Means، دو تفاوت اصلی این دو الگوریتم در چه مواردی است؟
• چرا انتخاب دقیق پارامتر Epsilon (ε) در الگوریتم DBSCAN اهمیت دارد؟
• الگوریتم DBSCAN چگونه توانایی پیدا کردن خوشه‌ها با شکل‌های متنواع را دارد؟

هفت‌خوان‌پلاس

برای بالابردن شانس‌تان می‌توانید این مطلب را هم مطالعه کنید و به پرسش‌های آن پاسخ دهید:

با برترین کاربردهای یادگیری عمیق در صنایع مختلف آشنا شوید!